はじめに
皆さんこんにちは、kon2です![]()
![]()
普段は大学でリチウム電池の負極材料に関する研究をしている学生です。
リチウムイオン電池は、携帯電話や電気自動車など、身の回りで幅広く活用されています。
最近ノーベル賞を受賞したことで、名前をよく聞くようになりましたね。
リチウムイオン電池は商用化から40年以上経っているもののまだまだ活発な研究分野で、最近は機械学習の活用が注目されています。
たとえば、新しい電極材料や電解液の開発や、電池構成(電極膜厚,電解液濃度,添加物...)の最適化、電池寿命の予測など……。
今回は、株式会社QuantumCore様が期間限定で提供しているQoreSDKを使って、リチウムイオン電池の放電容量の時系列予測を行ってみようと思います![]()
![]()
![]()
QoreSDKに関する紹介・使い方は、以下の記事で解説されています
リザーバコンピューティングの世界 ~Qoreとともに~
QoreSDKの紹介とQoreで不整脈検出
せっかくなので、深層学習の1種であるLSTMを用いて同様の学習を行い、結果を比較してみました。
充放電データの取得
充放電データは、メリーランド大学のCALCE(Center for Advanced Life Cycle Engineering)によって以下のページで公開されているデータを用います。
本解析では、CS2 Batteryの充放電データ(CS2-35, CS2-36, CS2-37,CS2-38)を使います。
Zip形式でダウンロード後、解凍したフォルダ内にあるxlsxファイルが充放電のデータです。
複数のデータに分かれているうえサイクル数もバラバラなので、適当にデータを整形、前処理します。
前処理に関しては本記事では解説しません、一応Jupyter-Notebook形式でGitHubに投稿しておいたので、こちらを参考にしてください![]()
![]()
![]()
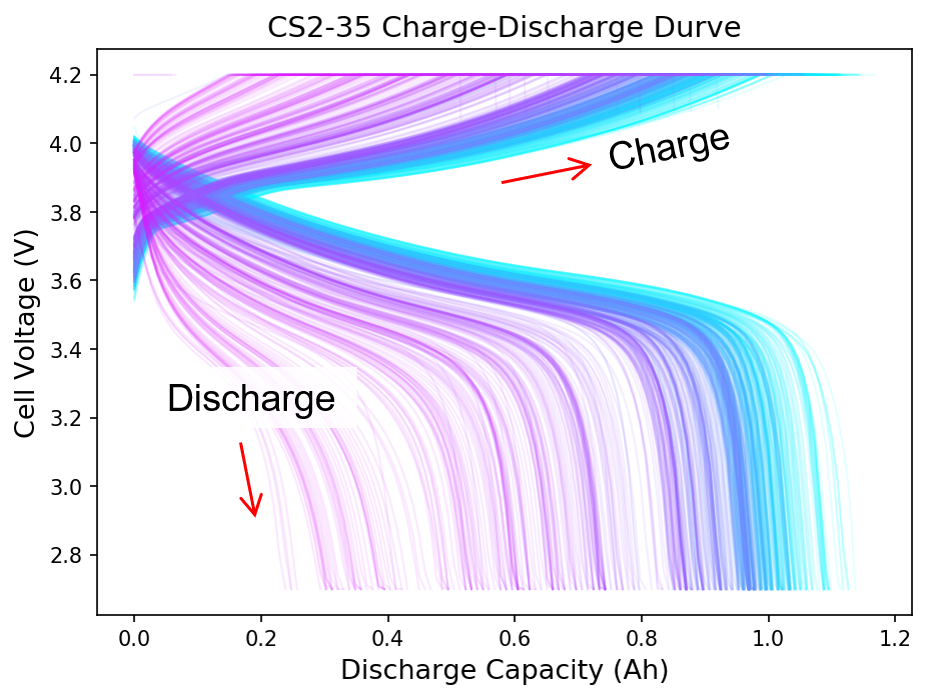
前処理後の電池CS2-35の充放電カーブがこちらです。総サイクル数は887サイクルでした。
右上に伸びているのが充電(Charge)、左下に伸びているのが放電(Discharge)カーブです。色が青から紫になるにつれて、サイクルが進行していることを示します。
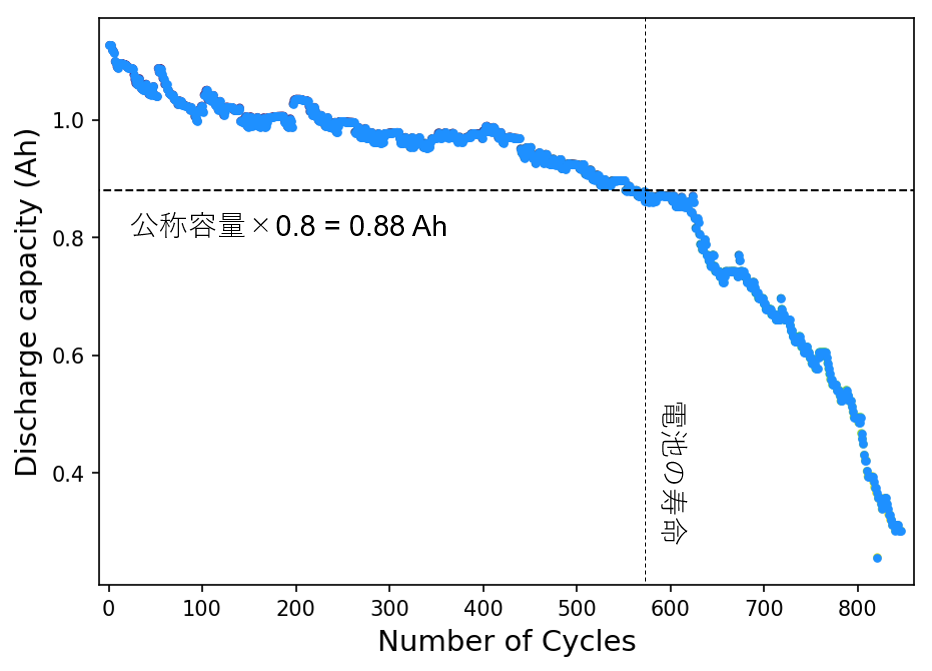
ここで知りたいのは電池のサイクルごとの最大放電容量(Discharge Capacity)です。これをサイクル数に対してプロットした図が以下になります。
サイクルとともに放電容量がどんどん少なくなっていることがわかります。
一般的には容量が20 %減少したところ(今回は1.1×0.8=0.88 Ah)が寿命の基準なので、この電池はだいたい580サイクル程度で耐用期間となります。
Qoreを用いた時系列解析
二次電池の放電容量とサイクル数の関係は時系列データとしてみなせるので、ARIMA(深層学習ではない)やLSTM(深層学習)などによる予測がこれまでに行われてきました。
Lithium-ion batteries remaining useful life prediction based on a mixture of empirical mode decomposition and ARIMA model (ARIMAを使った論文)
Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries(LSTMを使った論文)
Assessing the Health of LiFePO4 Traction Batteries through Monotonic Echo State Networks
(Echo State Networkを使った論文)
最後の論文は、リザーバコンピューティングの一種であるEcho State Networksを予測に使っている論文です。
まさか既にやっている人がいるとは思わなかった。
とにかく、QoreSDKが提供するリザーバコンピューティングは時系列解析を得意とする、とのことなので、これを用いて同じような時系列解析を行っていこうと思います。
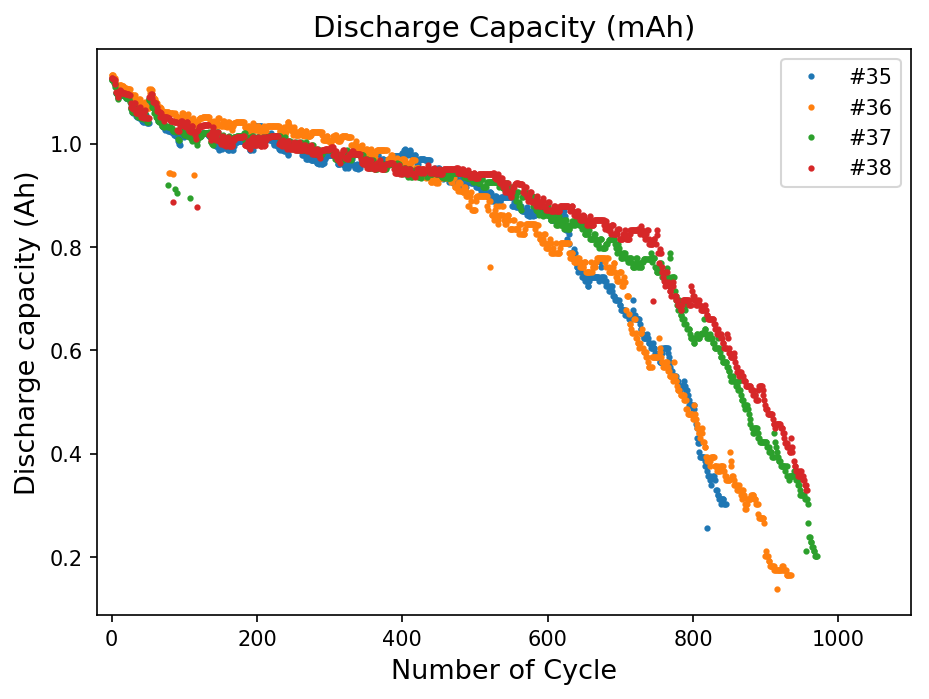
今回用いる学習データの一覧はこちら。
この4つのリチウムイオン電池の充放電データのうちから、3種類(#35, 37, 38)を教師データに、1種類(#36)をテストデータとして時系列解析を行っていきます。
時系列解析の方もJupyter-notebookで公開しているので、ぜひご覧ください。
以下では簡単な解説をします。
データの読み込みと教師データの作成
まずはcsv形式のデータを読み込みます。
念のために欠損値処理もしておきます。
df_35 = pd.read_csv('CS2_35.csv',index_col=0).dropna()
df_36 = pd.read_csv('CS2_36.csv',index_col=0).dropna()
df_37 = pd.read_csv('CS2_37.csv',index_col=0).dropna()
df_38 = pd.read_csv('CS2_38.csv',index_col=0).dropna()
以下の関数を用いて時系列解析用の教師データを作成します。同じようにQoreSDKを使っている下の記事を参考にさせていただきました![]()
![]()
![]()
def ConvertData(dataset,t_width):
X_trains = []
y_trains = []
for df in dataset:
t_length = len(df)
train_x = np.arange(t_length)
capacity = np.array(df['capacity'])
train_y = capacity
for i in range(t_length - t_width):
X_trains.append(train_y[i:i + t_width])
y_trains.append(train_y[i + t_width])
X_trains = np.array(X_trains)
y_trains = np.array(y_trains)
return X_trains,y_trains
X_train,y_train = ConvertData([df_35,df_37,df_38],50)
X_test,y_test = ConvertData([df_36],50)
この処理で得られた教師データの次元を確認します。
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)
>> (2588, 50) (873, 50) (2588,) (873,)
APIに投げるにはデータが多すぎるので、教師データの数を500に減らします。
データの選出はランダムに行います。
idx = np.arange(0,X_train.shape[0],1)
idx = np.random.permutation(idx)
idx_lim = idx[:500]
X_train = X_train[idx_lim]
y_train = y_train[idx_lim]
最後に、教師データを(データ数, 時間, 実データ)の次元に変換します。
と言っても多変量ではないので最後の次元は1ですが。
X_train = X_train.reshape([X_train.shape[0], X_train.shape[1], 1])
X_test = X_test.reshape([X_test.shape[0], X_test.shape[1], 1])
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)
>> (500, 50, 1) (873, 50, 1) (500,) (873,)
こんな感じになります。
QoreSDKを用いた時系列データの学習
学習といってもネットワーク構造やパラメータの最適化をする必要がなく、APIに投げるだけなのでとても楽です。
%%time
client = WebQoreClient(username, password, endpoint=endpoint)
time_ = client.regression_train(X_train, y_train)
print('Time:', time_['train_time'], 's')
>> Time: 1.784491777420044 s
>> Wall time: 2.26 s
しかもすぐに結果が返ってくる。
ほんとに学習できているのか不安になるほど早いです。
確認してみましょう。まずはトレーニングデータから。
# 推論
res = client.regression_predict(X_train)
# プロット
fig=plt.figure(figsize=(12, 4),dpi=150)
plt.plot(res['Y'],alpha=0.7,label='Prediction')
plt.plot(y_train,alpha=0.7,label='True')
plt.legend(loc='upper right',fontsize=12)
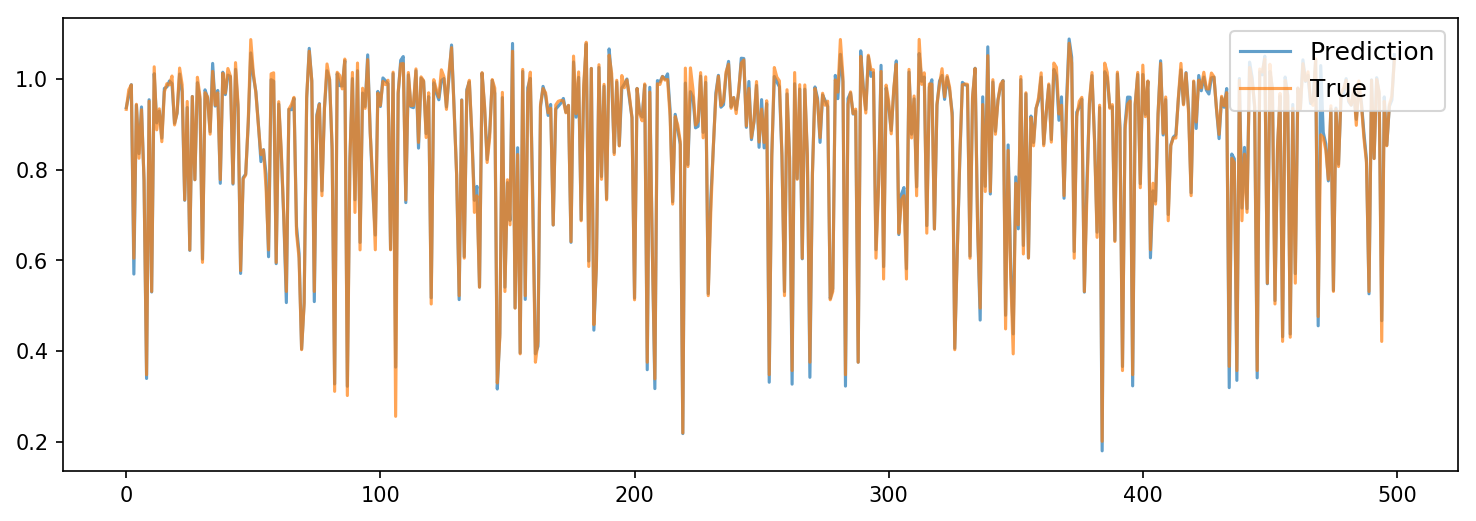
トレーニングデータの予測値を見る限り、学習はちゃんとできているようです。
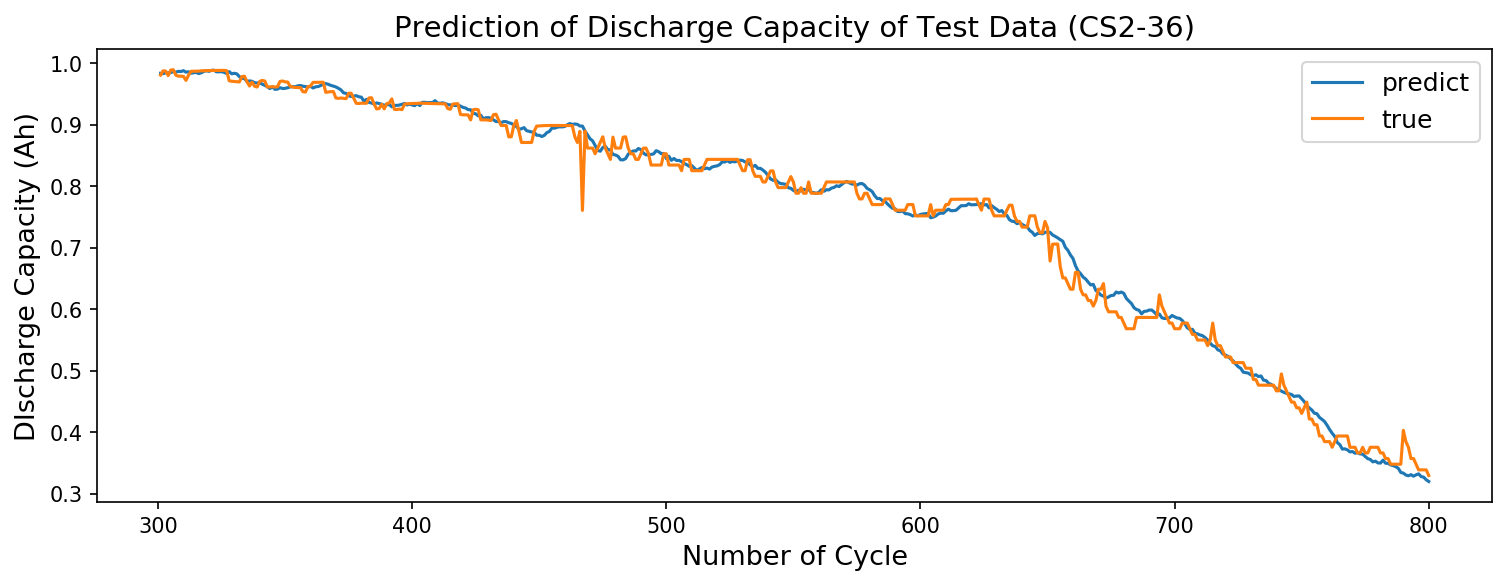
次に、テストデータである電池(#36)の300~800サイクルの放電容量の予測結果を表示します。
青が予測値、オレンジが実験値です。
結構いい感じに予測できてるんじゃないでしょうか?
誤差(MSE)の表示にはscikit-learnを使いました(後でLSTMと比較するため)。
from sklearn.metrics import mean_squared_error
print(mean_squared_error(y_test[300:800], res['Y']))
>> 0.00025365167122575003
それでは実際に、500から550サイクルまでの放電容量を以下のように予測してみます。
# 放電容量の未来予測
initial = X_test[500]
results = []
for i in tqdm(range(50)):
if(i == 0):
res = client.regression_predict([initial])['Y']
results.append(res[0])
time.sleep(1)
else:
initial = np.vstack((initial[1:],np.array(res)))
res = client.regression_predict([initial])['Y']
results.append(res[0])
time.sleep(1)
# プロット
fig=plt.figure(figsize=(12,4),dpi=150)
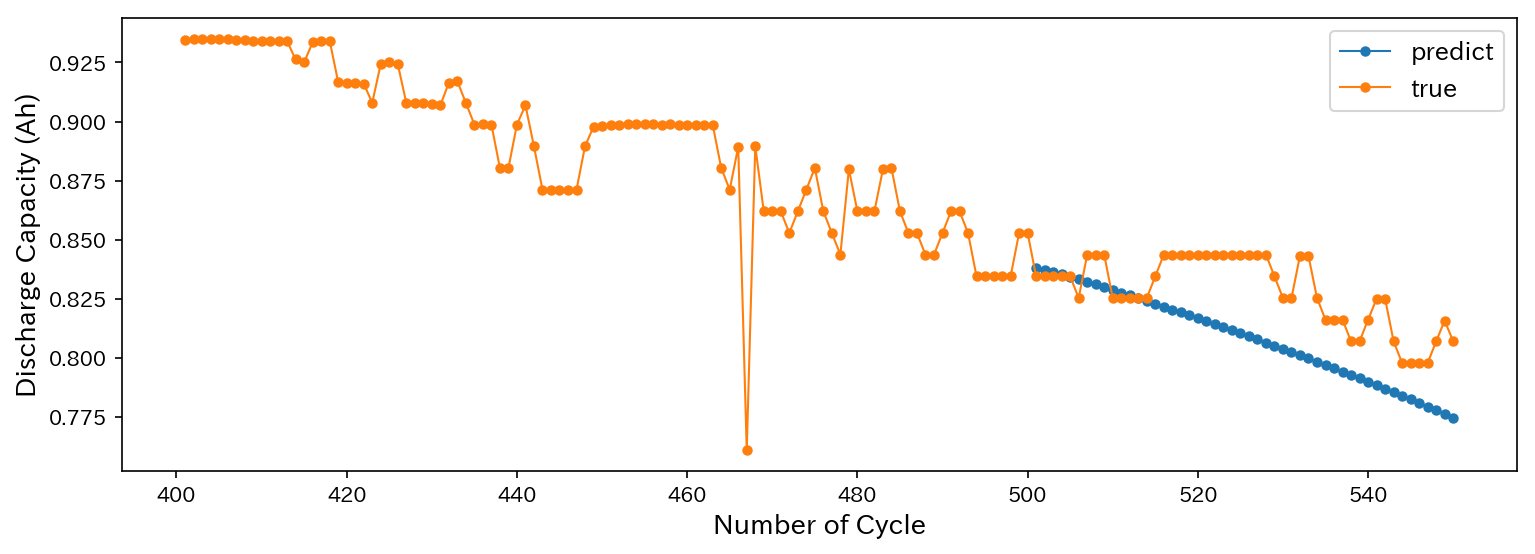
plt.plot(np.linspace(501,550,50),results,'o-',ms=4,lw=1,label='predict')
plt.plot(np.linspace(401,550,150),y_test[400:550],'o-',lw=1,ms=4,label='true')
plt.legend(loc='upper right',fontsize=12)
plt.xlabel('Number of Cycle',fontsize=13)
plt.ylabel('Discharge Capacity (Ah)',fontsize=13)
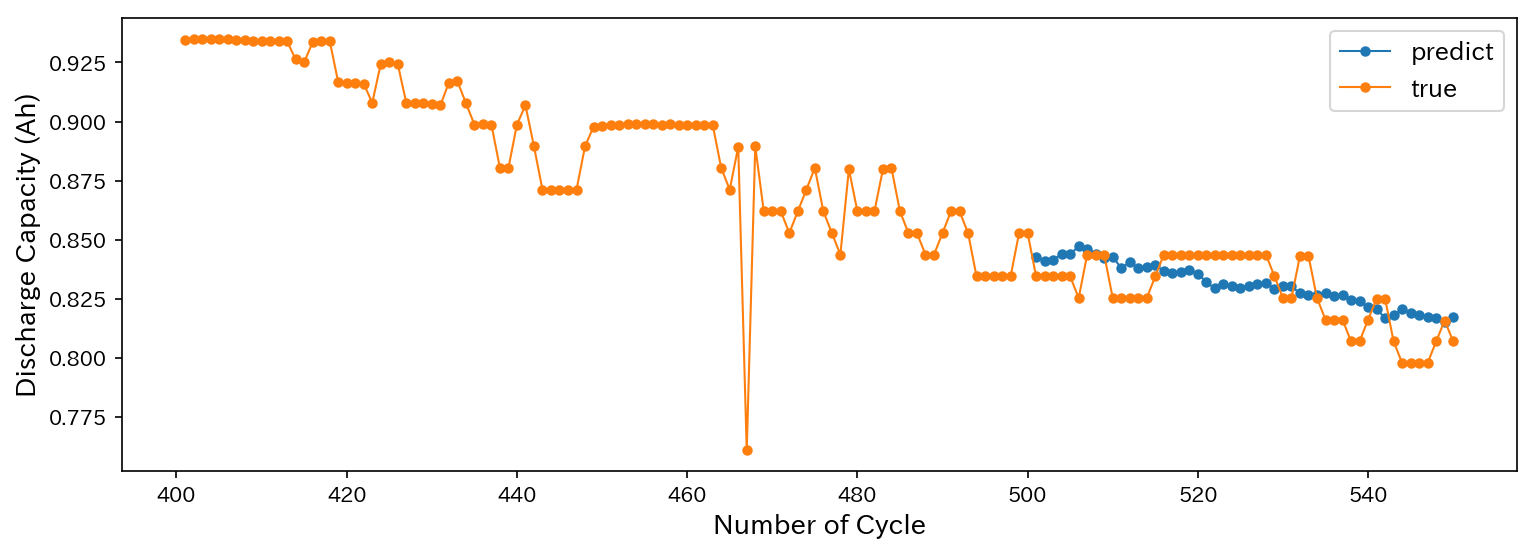
結果は以下の通り。
いい感じに予測できています!
LSTMによる学習
せっかくなのでLSTMと比較をしてみます。
まずは正解データの次元を(N, )から(N, 1)に変えます。
X_train = X_train.reshape([X_train.shape[0], X_train.shape[1], 1])
X_test = X_test.reshape([X_test.shape[0], X_test.shape[1], 1])
y_train = y_train.reshape([y_train.shape[0], 1])
y_test = y_test.reshape([y_test.shape[0], 1])
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)
>> (500, 50, 1) (873, 50, 1) (500, 1) (873, 1)
LSTMのパラメータは以下の通りです。
hidden layer:3
optimizer:rmsprop
loss function:mean squared error
batch size:50
epochs:100
モデルの構築と学習はこんな感じに行います。
# LSTMモデル構築
length_of_sequence = X_train.shape[1]
in_out_neurons = 1
n_hidden = 3
model = Sequential()
model.add(LSTM(n_hidden, batch_input_shape=(None, length_of_sequence, in_out_neurons),
return_sequences=False))
model.add(Dense(1))
model.add(Activation("linear"))
model.compile(loss="mean_squared_error", optimizer="rmsprop")
# モデル学習
%%time
early_stopping = EarlyStopping(monitor='val_loss', mode='auto', patience=20)
history = model.fit(X_train, y_train,
batch_size=50,
epochs=100,
validation_split=0.1,
callbacks=[early_stopping,PlotLossesKeras()]
)
GPU(GTX1070)を使用し、計算時間は1 min 27 sでした。
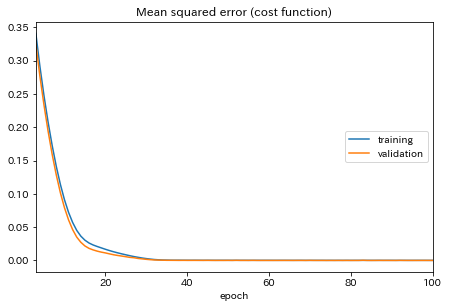
学習中のLossの推移は以下のようになります。
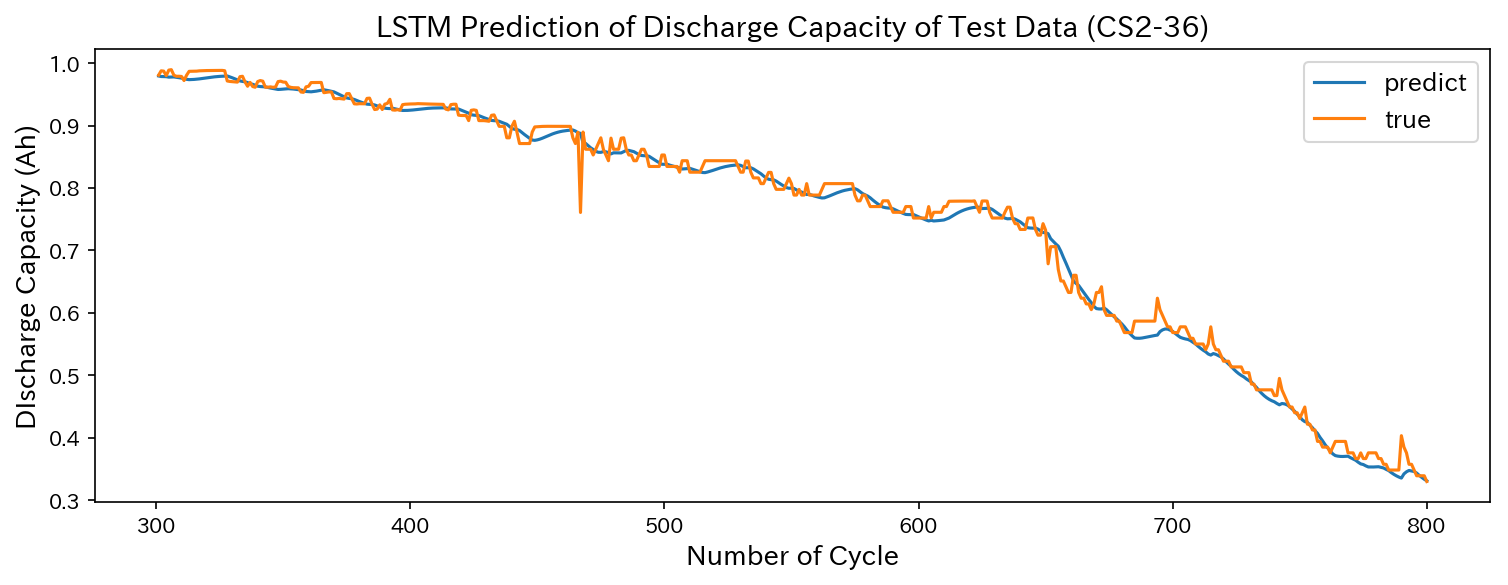
このモデルを使ってQoreの場合と同様にテストデータ(CS2-36)の放電容量を予測した結果はこちら。
同じように予測できてます。MSEは0.00021017となりました。
では先ほどと同じように、500から550サイクルまでの放電容量を以下のように予測します。
initial = X_test[500]
results = []
for i in tqdm(range(50)):
if(i == 0):
initial = initial.reshape(1,50,1)
res = model.predict(initial)
results.append(res[0][0])
else:
initial = initial.reshape(50,1)
initial = np.vstack((initial[1:],np.array(res)))
initial = initial.reshape(1,50,1)
res = model.predict([initial])
results.append(res[0][0])
一応できているようですが……Qoreを使った時の方がよく予測できているように見えますね。
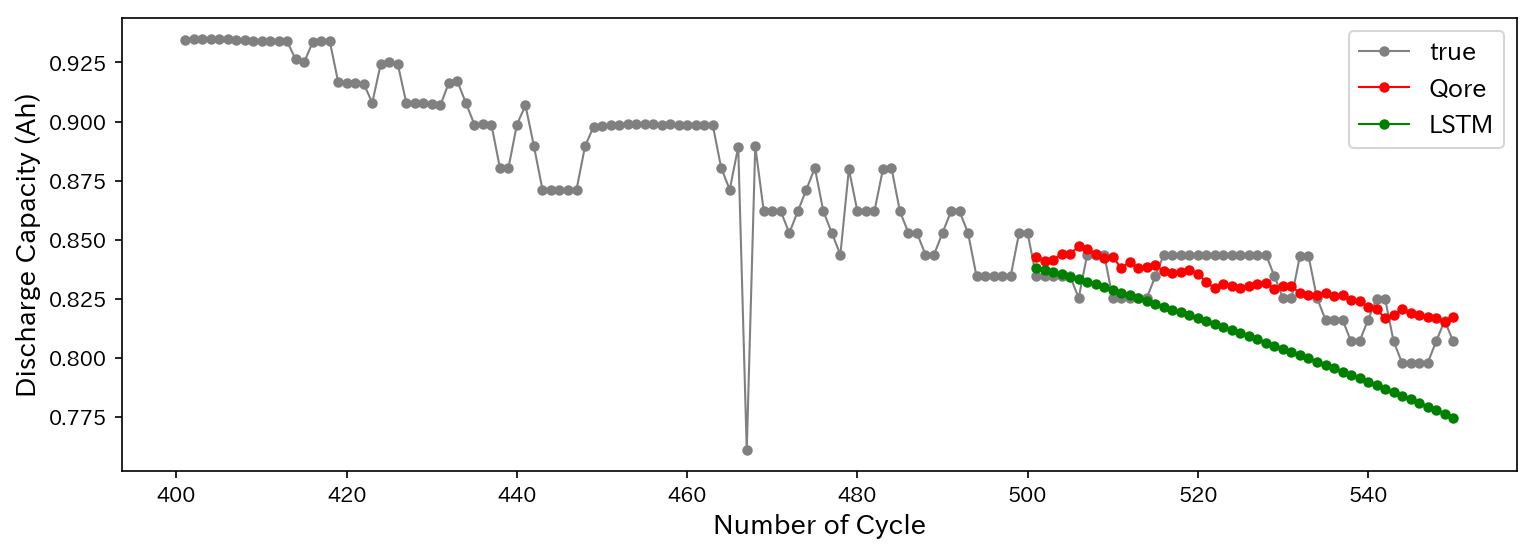
最後に、時系列予測の結果をQoreの場合と一緒にプロットした図を示します。
まとめ
今回の記事では、QoreSDKを用いたリチウムイオン電池の劣化過程(放電容量の減少)の時系列予測を行い、一般的に用いられるLSTMを用いた場合と比較しました。
その結果、テストデータとの誤差(mse)と計算時間は以下のようになりました。
| QoreSDK | LSTM | |
|---|---|---|
| MSE | 2.5365e-4 | 2.1017e-4 |
| 学習時間 | 1.78 s | 87 s |
誤差はLSTMの方がやや小さいですが、学習時間はQoreの方が圧倒的に速いです。
学習パラメータの調整なしにここまで学習できるのは驚きです。
最後に
今回行った電池の劣化予測は、実際のところまだまだ不十分です。
これは、時系列の予測に放電容量しか用いていないことが原因だと思われます。
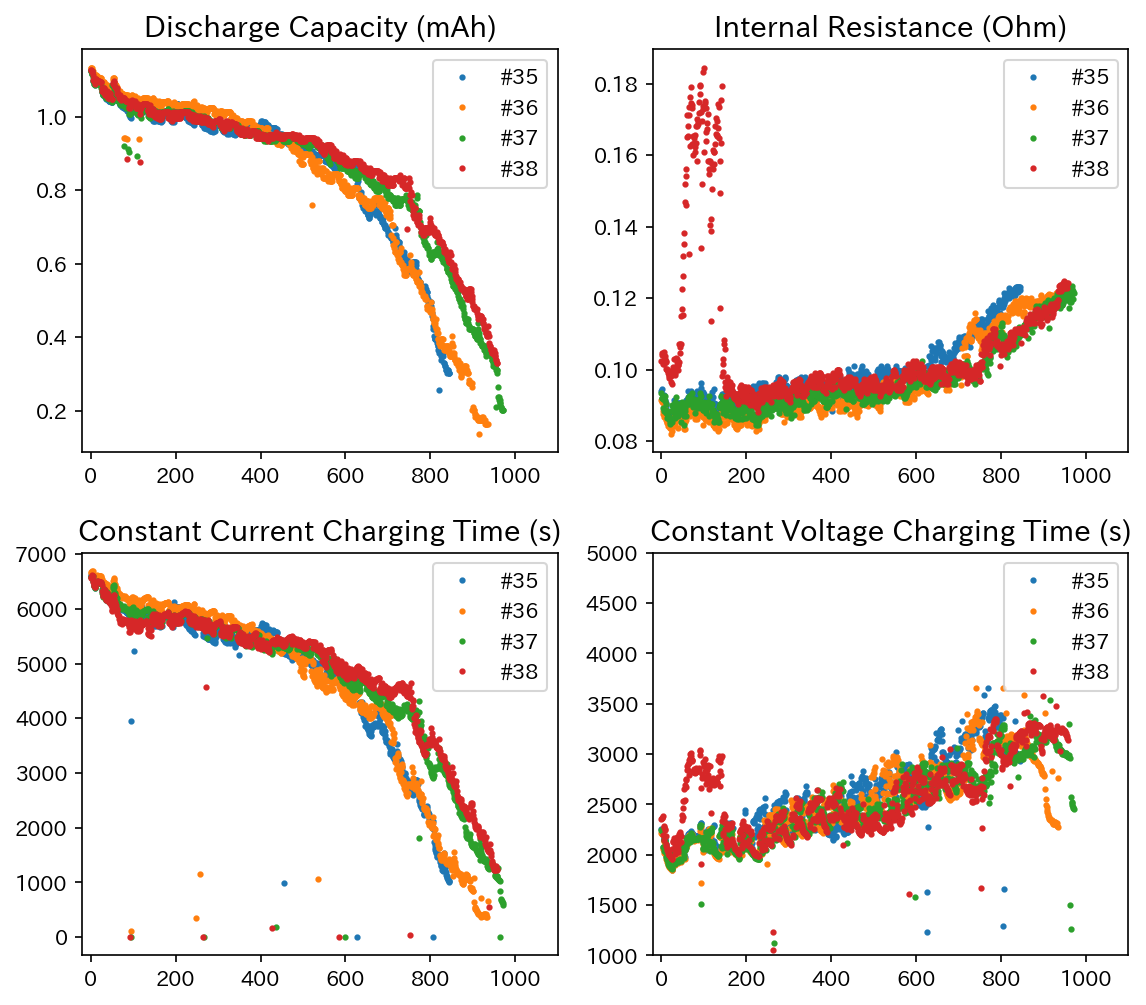
実際のところ、電池の容量に関連するパラメータは他にもたくさんあります。例えば、今回のデータセットからは、以下のようなデータが取得できます。
左上から放電容量、内部抵抗、定電流充電時間、定電圧充電時間と充放電サイクルの関係となります。
このあたりのデータも含めた多変量の時系列解析を行えば、もっと精度よく劣化予測が行えるはずです。
(今回は力が及びませんでした……)
Quantum Core様、今回はこのようなAPIを提供していただきありがとうございます。
時系列解析はど素人でしたが、とても面白かったです!
期間限定なので遊びたい人はぜひ![]()
![]()
![]()
深層学習以外の機械学習と応用技術 by QuantumCore Advent Calendar 2019
それでは~~。