目標: リー群に付随するリー代数を理解しよう
本記事は以下の内容を参考にしてまとめたものである。
ロボット工学のためのリー群・リー代数入門
1. 接ベクトル空間について
リー代数を扱う上で、接ベクトル空間の知識が必要なため、関連する用語の復習から入る。
1.1 ベクトル空間の復習
ベクトル空間 (Vector Space)
集合 $V$ が次の2条件を満たすとき、$V$を $\mathbb{R}$ 上のベクトル空間という。なお、$V$の元をベクトルと呼ぶ。
(I) ベクトルの加法 $+ : V \times V \to V$
任意の $\boldsymbol{u}, \boldsymbol{v} \in V$ に対し、$\boldsymbol{u} + \boldsymbol{v} \in V$ が定まり、次の法則が成り立つ。
- 加法の結合法則: $(\boldsymbol{u} + \boldsymbol{v}) + \boldsymbol{w} = \boldsymbol{u} + (\boldsymbol{v} + \boldsymbol{w})$
- 加法の交換法則: $\boldsymbol{u} + \boldsymbol{v} = \boldsymbol{v} + \boldsymbol{u}$
- 加法の単位元の存在: $\boldsymbol{0} \in V$ が存在し、$\boldsymbol{v} + \boldsymbol{0} = \boldsymbol{v}$
- 加法の逆元の存在: 各 $\boldsymbol{v} \in V$ に対し、$-\boldsymbol{v} \in V$ が存在し、$\boldsymbol{v} + (-\boldsymbol{v}) = \boldsymbol{0}$
(II) スカラー倍 $\cdot : \mathbb{R} \times V \to V$
任意の $c, d \in \mathbb{R}$、$\boldsymbol{v} \in V$ に対し、$c\boldsymbol{v} \in V$ が定まり、次の法則が成り立つ。
- スカラー和の分配法則: $(c + d)\boldsymbol{v} = c\boldsymbol{v} + d\boldsymbol{v}$
- ベクトル和の分配法則: $c(\boldsymbol{u} + \boldsymbol{v}) = c\boldsymbol{u} + c\boldsymbol{v}$
- スカラー積の結合法則: $(cd)\boldsymbol{v} = c(d\boldsymbol{v})$
- 単位スカラーの法則: $1\boldsymbol{v} = \boldsymbol{v}$
線型結合 (Linear Combination)
ベクトル空間 $V$ の元 $\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots,\boldsymbol{v}_k$ とスカラー $c_1,c_2,\ldots,c_k$ が与えられたとき、それらの線型結合は次のように定義される。
$$c_1\boldsymbol{v}_1+c_2\boldsymbol{v}_2+\cdots+c_k\boldsymbol{v}_k$$
一次独立 (Linear Independence)
ベクトル空間 $V$ のベクトルの集合 ${\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots,\boldsymbol{v}_k}$ が一次独立であるとは、以下の条件を満たすことである。
$$c_1\boldsymbol{v}_1+c_2\boldsymbol{v}_2+\cdots+c_k\boldsymbol{v}_k=\boldsymbol{0} \Rightarrow c_1=c_2=\cdots=c_k=0$$
ここで $\boldsymbol{0}$ は $V$ の零ベクトルである。
基底 (Basis)
ベクトル空間 $V$ のベクトルの集合 ${\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots,\boldsymbol{v}_n}$ が $V$ の基底であるとは、以下の2つの条件を満たすことである。
- ${\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots,\boldsymbol{v}_n}$ が一次独立である。
- $V$ の任意のベクトル $\boldsymbol{v}$ が ${\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots,\boldsymbol{v}_n}$ の元の線型結合として一意に表せる。
ベクトル空間の次元 (Dimension)
ベクトル空間$V$の基底の個数が$n$であるとき、$V$の次元は$n$であるといい、$\dim(V) = n$と表す。
1.2 接ベクトル、接ベクトル空間
ロボット工学のためのリー群・リー代数入門の 3. リー代数を参照。
1.3 線形リー群の自由度について
制約が加わることによってパラメータすなわち自由度(Degree of Freedom)が減る。
| 記号 | 自由度 (次元) | 制約条件 |
|---|---|---|
| $GL(n,\mathbb{R})$ | $n^2$ | なし |
| $SL(n,\mathbb{R})$ | $n^2-1$ | $\det(\boldsymbol{R}) = 1$ |
| $O(n)$ | $n(n-1)/2 = n^2 - \frac{n(n+1)}{2} $ | $\boldsymbol{R}^T \boldsymbol{R} = \boldsymbol{I}$ |
| $SO(n)$ | $n(n-1)/2 = n^2 - \frac{n(n+1)}{2} $ | $\boldsymbol{R}^T \boldsymbol{R} = \boldsymbol{I}, \det(\boldsymbol{R}) = 1$ |
例:
$SO(2)$の自由度は1
$SO(3)$の自由度は3
2. リー群に付随するリー代数
リー代数を定義するときの3つの解釈
- リー群の単位元の接空間から考える
- 指数写像から考える
- リー括弧積が定義されている空間から考える(未掲載)
2.1 リー群の単位元の接空間から考える
2.1.1 リー代数の定義1
あるリー群$G$における単位元$\boldsymbol{I}$の接空間を、$G$に付随するリー代数$\mathfrak{g}$と呼ぶ
2.1.2 例
$SO(3)$のリー代数$\mathfrak{so}(3)$を3つの基底とスカラーを用いて表してみよう。
まず、x軸まわりの角度$t$の回転$\boldsymbol{R}_x(t)$とその接ベクトルを考える。
x軸まわりの角度$t$の回転行列は次のように表される:
\boldsymbol{R}_x(t) = \begin{pmatrix}
1 & 0 & 0 \\
0 & \cos t & -\sin t \\
0 & \sin t & \cos t
\end{pmatrix}
$t = 0$のとき、$\boldsymbol{R}_x(0) = \boldsymbol{I}$(単位行列)を通る$SO(3)$上の曲線のため、t=0における微分は接ベクトルのひとつである。
\boldsymbol{J}_1 = \left.\frac{d}{dt}\boldsymbol{R}_x(t)\right|_{t=0} = \begin{pmatrix}
0 & 0 & 0 \\
0 & -\sin 0 & -\cos 0 \\
0 & \cos 0 & -\sin 0
\end{pmatrix} = \begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{pmatrix}
同様に、y軸, z軸まわりの角度$t$の回転$\boldsymbol{R}_y(t)$, $\boldsymbol{R}_z(t)$に対する接ベクトルは、
\boldsymbol{J}_2 = \left.\frac{d}{dt}\boldsymbol{R}_y(t)\right|_{t=0} = \begin{pmatrix}
-\sin 0 & 0 & \cos 0 \\
0 & 0 & 0 \\
-\cos 0 & 0 & -\sin 0
\end{pmatrix} = \begin{pmatrix}
0 & 0 & 1 \\
0 & 0 & 0 \\
-1 & 0 & 0
\end{pmatrix}
\boldsymbol{J}_3 = \left.\frac{d}{dt}\boldsymbol{R}_z(t)\right|_{t=0} = \begin{pmatrix}
-\sin 0 & -\cos 0 & 0 \\
\cos 0 & -\sin 0 & 0 \\
0 & 0 & 0
\end{pmatrix} = \begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0
\end{pmatrix}
$\boldsymbol{J}_1, \boldsymbol{J}_2, \boldsymbol{J}_3$は線形独立なためこれらを基底として、$\mathfrak{so}(3)$の任意の元$\boldsymbol{X}$はベクトル$\boldsymbol{\omega} = (\omega_1, \omega_2, \omega_3)^T \in \mathbb{R}^3$を用いて、
\boldsymbol{X} = \omega_1\boldsymbol{J}_1 + \omega_2\boldsymbol{J}_2 + \omega_3\boldsymbol{J}_3 =
\begin{pmatrix}
0 & -\omega_3 & \omega_2 \\
\omega_3 & 0 & -\omega_1 \\
-\omega_2 & \omega_1 & 0
\end{pmatrix}
と表すことができる。この$\boldsymbol{X}$は3×3の歪対称行列(skew-symmetric matrix)になっている。歪対称行列とは、その転置が自分自身の符号を反転させたものと等しい行列、つまり$\boldsymbol{X}^T = -\boldsymbol{X}$を満たす行列である。この性質により、$\mathrm{tr}(\boldsymbol{X}) = 0$, $\boldsymbol{X}_{ij} = -\boldsymbol{X}_{ji}$という関係を持つ。
2.2 指数写像から考える
2.2.1 リー代数の定義2
任意の実数$t$に対して$\exp(t\boldsymbol{X}) \in G$となるような$\boldsymbol{X}$の全体集合を、リー群$G$に付随するリー代数$\mathfrak{g}$とする。
expの由来が気になる場合はこちらを参照。行列微分方程式の解からきていることがわかる。
CV・CG・ロボティクスのためのリー群・リー代数入門: (1) リー群
2.2.2 例
$\boldsymbol{R}(t) = \exp(t\boldsymbol{X}) \in SO(3)$ としたときに、$\boldsymbol{R}(t)^T \boldsymbol{R}(t) = \boldsymbol{I}$と$\det(\boldsymbol{R}(t)) = 1$ の条件から、$X$がどのような条件をとるかを考えよう。
まず、$\boldsymbol{R}(t)^T \boldsymbol{R}(t) = \boldsymbol{I}$の両辺を $t$ で微分すると、積の微分法則により、
\frac{d}{dt}(\boldsymbol{R}(t)^T \boldsymbol{R}(t)) = \dot{\boldsymbol{R}}(t)^T \boldsymbol{R}(t) + \boldsymbol{R}(t)^T \dot{\boldsymbol{R}}(t) = 0
\dot{\boldsymbol{R}}(t) = \frac{d}{dt} \exp(t\boldsymbol{X}) = \boldsymbol{X} \exp(t\boldsymbol{X})
となる。
ここで、$t=0$ の場合を考える。
\dot{\boldsymbol{R}}(0) = \boldsymbol{X} \exp(0) = \boldsymbol{X}
\boldsymbol{R}(0) = \exp(0 \cdot \boldsymbol{X}) = \boldsymbol{I}
これらの結果を微分した式に代入すると、
\boldsymbol{X}^T + \boldsymbol{X} = 0 \quad \Leftrightarrow \quad \boldsymbol{X}^T = -\boldsymbol{X}
が得られる。これは、$\boldsymbol{X}$ が歪対称行列であることを示す。
また、$\det(\boldsymbol{R}(t)) = \det(\exp(t\boldsymbol{X})) = 1$ という条件について、行列指数関数におけるヤコビの公式 $\det(\exp(\boldsymbol{A})) = \exp(\mathrm{tr}(\boldsymbol{A}))$ を用いると、
\exp(\mathrm{tr}(t\boldsymbol{X})) = \exp(t \cdot \mathrm{tr}(\boldsymbol{X})) = 1
これが任意の $t$ で成立するためには、$\mathrm{tr}(\boldsymbol{X}) = 0$ である必要がある。
3x3の歪対称行列
\boldsymbol{X} = \begin{pmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{pmatrix}
のトレースは常に0であるため、この条件は自動的に満たされる。
📖 参照資料
3. SO(3)のリー代数so(3)の解釈
$\mathfrak{so}(3)$の元$X$は$\boldsymbol{\omega}$を用いて$X = \omega_1 J_1+ \omega_2J_2 + \omega_3J_3$と表せた。この$\boldsymbol{\omega}$の値が何を示しているか?については以下の2つの解釈があげられる。
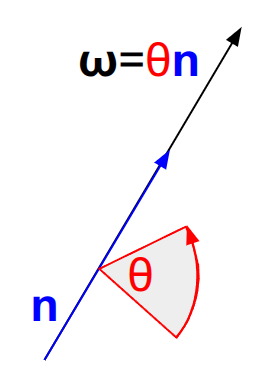
3.1 軸・角度表現 (axis-angle representation)
回転軸: $\boldsymbol{n} = \boldsymbol{\omega} / ||\boldsymbol{\omega}||$
回転角度: $\theta = ||\boldsymbol{\omega}||$
とした回転ベクトル $\boldsymbol{\omega} = \theta \boldsymbol{n}$ とみなすことができる。
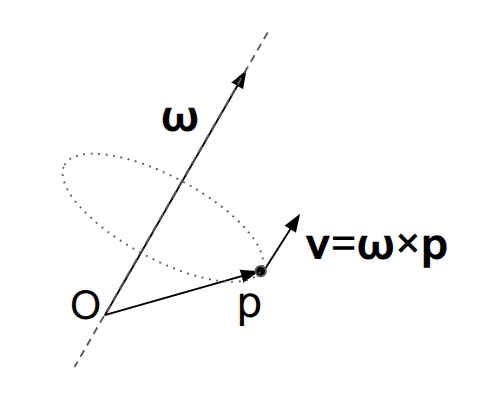
3.2 角速度ベクトル
原点を中心に回転する剛体上の点 $\boldsymbol{p}$ の速度 ${\boldsymbol{v}}$ は、角速度ベクトル $\boldsymbol{\omega}$ と位置ベクトル $\boldsymbol{p}$ の外積として表すことができる。
{\boldsymbol{v}} = \boldsymbol{\omega} \times \boldsymbol{p}= \begin{pmatrix} -\omega_3 p_2 + \omega_2 p_3 \\ \omega_3 p_1 - \omega_1 p_3 \\ -\omega_2 p_1 + \omega_1 p_2 \end{pmatrix}
この行列内の計算は、$X = [\boldsymbol{\omega}] _\times$とすると、$[\boldsymbol{\omega}]_\times \boldsymbol{p}$と同じとなる。したがって、$\boldsymbol{\omega}$は角速度ベクトルとみなすことができる。
📖 参照資料
まとめ
- $SO(3)$リー群に付随するリー代数$\mathfrak{so}(3)$は、単位元での接空間として定義され、
$3 \times 3$の歪対称行列で表現される。基底行列$\boldsymbol{J}_1, \boldsymbol{J}_2, \boldsymbol{J}_3$を用いて任意の元$\boldsymbol{X}$は
ベクトル$\boldsymbol{\omega}=(\omega_1,\omega_2,\omega_3)^T$の線形結合として表せる - リー代数の元$\boldsymbol{X}$は $\exp(t\boldsymbol{X}) \in SO(3)$ を満たす行列として特徴付けられ、
$SO(3)$の制約条件(直交性と$\det=1$)から、$\boldsymbol{X}$が歪対称行列($\boldsymbol{X}^T = -\boldsymbol{X}$)かつ
トレースが$0$という条件が導かれる - $\mathfrak{so}(3)$の元$\boldsymbol{\omega}$は軸・角度表現(回転軸$\boldsymbol{n} = \boldsymbol{\omega}/||\boldsymbol{\omega}||$、回転角度$\theta = ||\boldsymbol{\omega}||$)
または角速度ベクトル(剛体の回転運動における瞬間角速度)として物理的に解釈できる