[Lie-learning] 第3回指数写像・対数写像

Posted at 2025-09-17

目標：指数写像と対数写像を理解しよう

本記事はこちらを元に解説する
Lie Groups for 2D and 3D Transformations

1. 概要

1.1 指数写像と対数写像について

リー群とリー代数の間の変換は指数写像(Exponential map)、対数写像(Logarithmic map)を用いて行う。
(写像の復習)

指数写像は、リー代数 $\boldsymbol{\mathfrak{g}}$ の元を、対応するリー群 $G$ の元に写像する操作。

\exp: \boldsymbol{\mathfrak{g}} \to G

対数写像は、リー群 $G$ の元を、リー代数 $\boldsymbol{\mathfrak{g}}$ の元に写像する操作。

\log: G \to \boldsymbol{\mathfrak{g}}

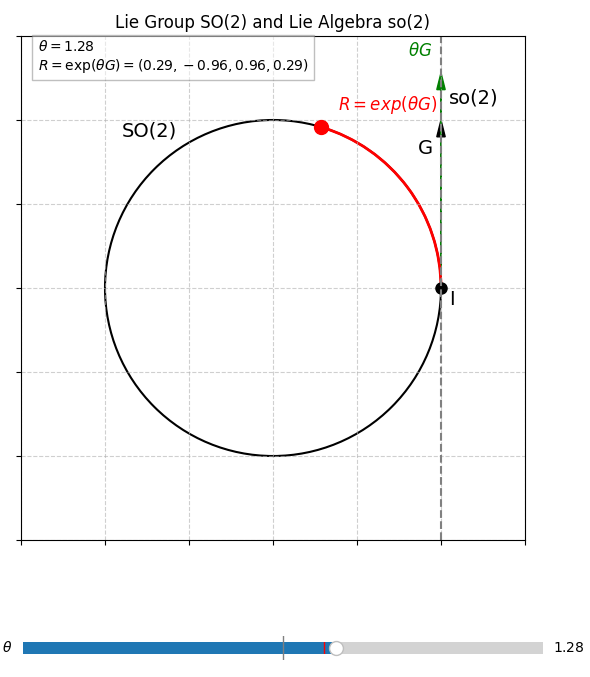
1.2 SO(2)でデモ

指数写像のデモ： exp_test.py

リー群

R = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \in SO(2)

リー代数

\theta \in \mathbb{R}, \quad J = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}, \\ \quad [\boldsymbol{\theta}]_\times = \begin{pmatrix} 0 & -\theta \\ \theta & 0 \end{pmatrix} \in \mathfrak{so}(2)

exp map

R = \exp([\boldsymbol{\theta}]_\times) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \in SO(2)

log map

\log(R) = [\boldsymbol{\theta}]_\times = \arctan({R_{12}},{R_{11}}) \in \mathfrak{so}(2)

$SO(2)$と$\mathfrak{so}(2)$の関係図

2. SO(3)

2.1 指数写像 (Exponential map)

計算式

[\boldsymbol{\omega}]_\times \in \mathfrak{so}(3), \quad \boldsymbol{\omega} \in \mathbb{R}^3, \quad \theta = \|\boldsymbol{\omega}\|

\exp([\boldsymbol{\omega}]_\times) = \boldsymbol{I} + \left( \frac{\sin \theta}{\theta} \right) [\boldsymbol{\omega}]_\times + \left( \frac{1 - \cos \theta}{\theta^2} \right) [\boldsymbol{\omega}]_\times^2

式の導出

$\mathfrak{so}(3)$ から $SO(3)$ への指数写像は、行列指数関数を用いて、次のようになる。

\exp([\boldsymbol{\omega}]_\times) = \exp \left( \begin{pmatrix} 
0 & -\omega_3 & \omega_2 \\ 
\omega_3 & 0 & -\omega_1 \\ 
-\omega_2 & \omega_1 & 0 
\end{pmatrix} \right) = \boldsymbol{I} + [\boldsymbol{\omega}]_\times + \frac{1}{2!} [\boldsymbol{\omega}]_\times^2 + \frac{1}{3!} [\boldsymbol{\omega}]_\times^3 + \dots

（参考：CV・CG・ロボティクスのためのリー群・リー代数入門: (2) 行列指数関数）

項をペアで書くと、次のようになる。

\exp([\boldsymbol{\omega}]_\times) = \boldsymbol{I} + \sum_{i=0}^{\infty} \left[ \frac{1}{(2i+1)!} [\boldsymbol{\omega}]_\times^{2i+1} + \frac{1}{(2i+2)!} [\boldsymbol{\omega}]_\times^{2i+2} \right]

ここで、歪対称行列の特性を利用する。

[\boldsymbol{\omega}]_\times^3 = -(\boldsymbol{\omega}^T \boldsymbol{\omega}) \cdot [\boldsymbol{\omega}]_\times

\theta^2 \equiv \boldsymbol{\omega}^T \boldsymbol{\omega}

$[\boldsymbol{\omega}] _\times$を3回かけると、元の$[\boldsymbol{\omega}] _\times$にスカラー$-\theta^2$をかけたものに戻るという周期的な性質を持っている。従って、次のような一般式で表せる。

[\boldsymbol{\omega}]_\times^{2i+1} = (-1)^i \theta^{2i} [\boldsymbol{\omega}]_\times

[\boldsymbol{\omega}]_\times^{2i+2} = (-1)^i \theta^{2i} [\boldsymbol{\omega}]_\times^2

指数写像の級数を因数分解して、係数のテイラー展開を以下のように閉形式で表すことができる。

\begin{align}
\exp([\boldsymbol{\omega}]_\times) &= \boldsymbol{I} + \left( \sum_{i=0}^{\infty} \frac{(-1)^i \theta^{2i}}{(2i+1)!} \right) [\boldsymbol{\omega}]_\times + \left( \sum_{i=0}^{\infty} \frac{(-1)^i \theta^{2i}}{(2i+2)!} \right) [\boldsymbol{\omega}]_\times^2 \tag{1}\\
&= \boldsymbol{I} + \left( 1 - \frac{\theta^2}{3!} + \frac{\theta^4}{5!} - \dots \right) [\boldsymbol{\omega}]_\times + \left( \frac{1}{2!} - \frac{\theta^2}{4!} + \frac{\theta^4}{6!} - \dots \right) [\boldsymbol{\omega}]_\times^2 \tag{2}\\
&= \boldsymbol{I} + \left( \frac{\sin \theta}{\theta} \right) [\boldsymbol{\omega}]_\times + \left( \frac{1 - \cos \theta}{\theta^2} \right) [\boldsymbol{\omega}]_\times^2 \tag{3}
\end{align}

式(2)から式(3)への変換は、$\sin \theta$と$\cos \theta$のテイラー展開を利用している。

\sin \theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \dots

\cos \theta = 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \dots

式(3)は有名なロドリゲスの公式である。指数写像の結果は、$\boldsymbol{\omega}$ によって与えられる軸周りを $\theta$ ラジアン回転することになる。

$\theta$ が小さい場合は、式(2)のように係数$\left( \frac{\sin \theta}{\theta} \right)$と$\left( \frac{1 - \cos \theta}{\theta^2} \right)$のテイラー展開（機械精度を考慮して適切な項数を選択）を使用するべきである。

2.2 対数写像 (Logarithm map)

計算式

\boldsymbol{R} \in SO(3), \quad \theta = \arccos\left(\frac{\mathrm{tr}(\boldsymbol{R}) - 1}{2}\right)

\ln(\boldsymbol{R}) = \frac{\theta}{2\sin\theta} \cdot (\boldsymbol{R} - \boldsymbol{R}^T)

式の導出

Logmapは指数写像の逆の操作であるため、指数写像の式から導出する。

$\theta$ の導出

式(3)の両辺のトレース（trace, 対角成分の和）を計算する。各項のトレースは以下のようになる。

$\mathrm{tr}(\boldsymbol{I}) = 3$
$\mathrm{tr}([\boldsymbol{\omega}]_\times) = 0$ （歪対称行列の対角成分は全て0のため）
$\mathrm{tr}([\boldsymbol{\omega}]_\times^2) = -2\theta^2$ （$[\boldsymbol{\omega}]_\times^2 = \boldsymbol{\omega}\boldsymbol{\omega}^T - (\boldsymbol{\omega}^T\boldsymbol{\omega})\boldsymbol{I}$ と $\theta^2 = \boldsymbol{\omega}^T\boldsymbol{\omega}$ より）

これらを使って式(3)のトレースを計算すると、

\begin{align}
\mathrm{tr}(\boldsymbol{R}) &= \mathrm{tr}(\boldsymbol{I}) + \left( \frac{\sin \theta}{\theta} \right) \mathrm{tr}([\boldsymbol{\omega}]_\times) + \left( \frac{1 - \cos \theta}{\theta^2} \right) \mathrm{tr}([\boldsymbol{\omega}]_\times^2) \notag \\
&= 3 + \left( \frac{\sin \theta}{\theta} \right) \cdot 0 + \left( \frac{1 - \cos \theta}{\theta^2} \right) (-2\theta^2) \notag \\
&= 3 - 2(1 - \cos \theta) \notag \\
&= 1 + 2\cos \theta \notag
\end{align}

この式を $\theta$ について解くと、目的の式が得られる。

\cos \theta = \frac{\mathrm{tr}(\boldsymbol{R}) - 1}{2} \quad \Rightarrow \quad \theta = \arccos\left(\frac{\mathrm{tr}(\boldsymbol{R}) - 1}{2}\right)

$[\boldsymbol{\omega}]_\times$ の導出

$\boldsymbol{R}^T$ は、歪対称行列の性質 $([\boldsymbol{\omega}]_\times)^T = -[\boldsymbol{\omega}]_\times$ と、対称行列の性質 $([\boldsymbol{\omega}]_\times^2)^T = [\boldsymbol{\omega}]_\times^2$ を使うと、以下のようになる。

\boldsymbol{R}^T = \boldsymbol{I} - \left( \frac{\sin \theta}{\theta} \right) [\boldsymbol{\omega}]_\times + \left( \frac{1 - \cos \theta}{\theta^2} \right) [\boldsymbol{\omega}]_\times^2 \quad \cdots \tag{4}

式(3)から式(4)を引くと、

\boldsymbol{R} - \boldsymbol{R}^T = 2 \frac{\sin \theta}{\theta} [\boldsymbol{\omega}]_\times

この式を $[\boldsymbol{\omega}]_\times$ について解く。$\ln(\boldsymbol{R}) = [\boldsymbol{\omega}]_\times$ であるため、これがLogmapの式となる。

\ln(\boldsymbol{R}) = [\boldsymbol{\omega}]_\times = \frac{\theta}{2\sin\theta} (\boldsymbol{R} - \boldsymbol{R}^T)

$\theta$が0に近い場合は、係数$\frac{\theta}{2\sin\theta}$のテイラー展開を使用すべきである。

2.3 実装

💻ソースコードを参照する

回転に関する実装：Rot3.h
指数写像の実装：SO3.cpp gtsam::so3::ExpmapFunctor::expmap()
$\theta$が0に近い場合の処理：SO3.cpp gtsam::so3::ExpmapFunctor::init()
対数写像の実装：SO3.cpp gtsam::SO3::Logmap()

⌨実装例

#include <gtsam/geometry/Rot3.h>
#include <iostream>

int main() {
    using namespace gtsam;

    // 適当な回転行列
    Rot3 R = Rot3::RzRyRx(0.1, -0.2, 0.3);

    // 回転行列 -> 回転ベクトル
    Vector3 omega = R.log();

    // 回転ベクトル -> 回転行列
    Rot3 R_recovered = Rot3::Expmap(omega);

    return 0;
}

3. SE(3)

3.1 指数写像 (Exponential map)

計算式

\boldsymbol{\delta} = (\boldsymbol{u} \quad \boldsymbol{\omega}) \in \mathbb{R}^3, \quad \theta = \|\boldsymbol{\omega}\|

\boldsymbol{\delta}^\wedge = \begin{pmatrix}
[\boldsymbol{\omega}]_\times & \boldsymbol{u} \\
0 & 0
\end{pmatrix} \in \mathfrak{se}(3)

A = \frac{\sin \theta}{\theta}, \quad B = \frac{1 - \cos \theta}{\theta^2}, \quad C = \frac{1 - A}{\theta^2}

\boldsymbol{R} = \boldsymbol{I} + A[\boldsymbol{\omega}]_\times + B[\boldsymbol{\omega}]_\times^2

V = \boldsymbol{I} + B[\boldsymbol{\omega}]_\times + C[\boldsymbol{\omega}]_\times^2

\exp\left(
\begin{pmatrix}
\boldsymbol{u} \\
\boldsymbol{\omega}
\end{pmatrix}
\right) = \begin{pmatrix} \boldsymbol{R} & V\boldsymbol{u} \\ 0 & 1 \end{pmatrix}

式の導出

$\mathfrak{se}(3)$ から$SE(3)$への指数写像は、行列指数関数を用いると、以下のようになる。

\boldsymbol{\delta}^\wedge = \begin{pmatrix}
[\boldsymbol{\omega}]_\times & \boldsymbol{u} \\
0 & 0
\end{pmatrix} \in \mathfrak{se}(3)

\exp(\boldsymbol{\delta}) = \boldsymbol{I} + \boldsymbol{\delta} + \frac{1}{2!}\boldsymbol{\delta}^{\wedge^{2}} + \frac{1}{3!}\boldsymbol{\delta}^{\wedge^{3}} + \cdots

ここで、

\boldsymbol{\delta}^{\wedge^{2}} = \begin{pmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{u} \\ 0 & 0 \end{pmatrix} \begin{pmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{u} \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} [\boldsymbol{\omega}]_\times^2 & [\boldsymbol{\omega}]_\times \boldsymbol{u} \\ 0 & 0 \end{pmatrix}

\boldsymbol{\delta}^{\wedge^{3}} = \begin{pmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{u} \\ 0 & 0 \end{pmatrix} \begin{pmatrix} [\boldsymbol{\omega}]_\times^2 & [\boldsymbol{\omega}]_\times \boldsymbol{u} \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} [\boldsymbol{\omega}]_\times^3 & [\boldsymbol{\omega}]_\times^2 \boldsymbol{u} \\ 0 & 0 \end{pmatrix}

なので、

\exp(\boldsymbol{\delta}^\wedge) = \boldsymbol{I} + \begin{pmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{u} \\ 0 & 0 \end{pmatrix} + \frac{1}{2!} \begin{pmatrix} [\boldsymbol{\omega}]_\times^2 & [\boldsymbol{\omega}]_\times \boldsymbol{u} \\ 0 & 0 \end{pmatrix} + \frac{1}{3!} \begin{pmatrix} [\boldsymbol{\omega}]_\times^3 & [\boldsymbol{\omega}]_\times^2 \boldsymbol{u} \\ 0 & 0 \end{pmatrix} + \cdots

回転ブロックは$SO(3)$と同じであるが、並進成分は異なるべき級数になる。

\exp\left(
\begin{pmatrix}
[\boldsymbol{\omega}]_\times & \boldsymbol{u} \\
0 & 0
\end{pmatrix}
\right) = \begin{pmatrix} \exp([\boldsymbol{\omega}]_\times) & V\boldsymbol{u} \\ 0 & 1 \end{pmatrix}

V = \boldsymbol{I} + \frac{1}{2!}[\boldsymbol{\omega}]_\times + \frac{1}{3!}[\boldsymbol{\omega}]_\times^2 + \cdots

項を奇数乗と偶数乗に分割し、因数分解する。

V = \boldsymbol{I} + \sum_{i=0}^{\infty} \left[\frac{1}{(2i+2)!}[\boldsymbol{\omega}]_\times^{2i+1} + \frac{1}{(2i+3)!}[\boldsymbol{\omega}]_\times^{2i+2}\right]

= \boldsymbol{I} + \left( \sum_{i=0}^{\infty} \frac{(-1)^i \theta^{2i}}{(2i+2)!} \right) [\boldsymbol{\omega}]_\times + \left( \sum_{i=0}^{\infty} \frac{(-1)^i \theta^{2i}}{(2i+3)!} \right) [\boldsymbol{\omega}]_\times^2

係数はテイラー展開で、

\sum_{i=0}^{\infty} \frac{(-1)^i \theta^{2i}}{(2i+2)!} = \frac{1}{2!} - \frac{\theta^2}{4!} + \frac{\theta^4}{6!} - \cdots = \frac{1 - \cos \theta}{\theta^2}

\sum_{i=0}^{\infty} \frac{(-1)^i \theta^{2i}}{(2i+3)!} = \frac{1}{3!} - \frac{\theta^2}{5!} + \frac{\theta^4}{7!} - \cdots = \frac{\theta - \sin \theta}{\theta^3}

となり、Vは以下のようにまとめられる。

V = \boldsymbol{I} + \left( \frac{1 - \cos \theta}{\theta^2} \right) [\boldsymbol{\omega}]_\times + \left( \frac{\theta - \sin \theta}{\theta^3} \right) [\boldsymbol{\omega}]_\times^2

$\theta^2$が小さい場合、$A, B, C$のテイラー展開を使用すべきである。

3.2 対数写像 (Logarithm map)

計算式

T = \begin{pmatrix} \boldsymbol{R} & \boldsymbol{t} \\ 0 & 1 \end{pmatrix} \in SE(3), \quad
\ln(T) = \begin{pmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{u} \\ 0 & 0 \end{pmatrix} \in \mathfrak{se}(3)

回転部分の$\ln$は $SO(3)$ と同様である。
並進部分は次で与えられる。

\boldsymbol{u} = V^{-1}\,\boldsymbol{t}

V^{-1} = \boldsymbol{I} - \frac{1}{2} [\boldsymbol{\omega}]_\times + \frac{1}{\theta^2} \left(1 - \frac{A}{2B}\right) [\boldsymbol{\omega}]_\times^2

導出

指数写像において、$V$は以下のように定義された。

V = \boldsymbol{I} + A[\boldsymbol{\omega}]_\times + B[\boldsymbol{\omega}]_\times^2

ここで、$A = \frac{1-\cos\theta}{\theta^2}$、$B = \frac{\theta-\sin\theta}{\theta^3}$である。

$V^{-1}$を求めるために、$V$の逆行列を直接計算する代わりに、$V$と同じ形の行列を仮定する。

V^{-1} = \boldsymbol{I} + \alpha[\boldsymbol{\omega}]_\times + \beta[\boldsymbol{\omega}]_\times^2

$V \cdot V^{-1} = \boldsymbol{I}$の条件から、係数$\alpha$と$\beta$を求める。

(\boldsymbol{I} + A[\boldsymbol{\omega}]_\times + B[\boldsymbol{\omega}]_\times^2)(\boldsymbol{I} + \alpha[\boldsymbol{\omega}]_\times + \beta[\boldsymbol{\omega}]_\times^2) = \boldsymbol{I}

左辺を展開すると：

\begin{align}
&= \boldsymbol{I} + \alpha[\boldsymbol{\omega}]_\times + \beta[\boldsymbol{\omega}]_\times^2 \nonumber \\
&\quad + A[\boldsymbol{\omega}]_\times + A\alpha[\boldsymbol{\omega}]_\times^2 + A\beta[\boldsymbol{\omega}]_\times^3 \nonumber \\
&\quad + B[\boldsymbol{\omega}]_\times^2 + B\alpha[\boldsymbol{\omega}]_\times^3 + B\beta[\boldsymbol{\omega}]_\times^4 \nonumber
\end{align}

$[\boldsymbol{\omega}]_\times^3 = -\theta^2[\boldsymbol{\omega}]_\times$および$[\boldsymbol{\omega}]_\times^4 = -\theta^2[\boldsymbol{\omega}]_\times^2$の性質を用いて整理すると：

\begin{align}
&= \boldsymbol{I} + (A + \alpha)[\boldsymbol{\omega}]_\times \nonumber \\
&\quad + (B + A\alpha + \beta)[\boldsymbol{\omega}]_\times^2 \nonumber \\
&\quad + (-A\beta\theta^2 - B\alpha\theta^2)[\boldsymbol{\omega}]_\times \nonumber \\
&\quad + (-B\beta\theta^2)[\boldsymbol{\omega}]_\times^2 \nonumber
\end{align}

= \boldsymbol{I} + (A + \alpha - A\beta\theta^2 - B\alpha\theta^2)[\boldsymbol{\omega}]_\times + (B + A\alpha + \beta - B\beta\theta^2)[\boldsymbol{\omega}]_\times^2

これが$\boldsymbol{I}$に等しくなるためには、各次数の係数がゼロでなければならない：

$[\boldsymbol{\omega}]_\times$の係数：$A + \alpha - A\beta\theta^2 - B\alpha\theta^2 = 0$
$[\boldsymbol{\omega}]_\times^2$の係数：$B + A\alpha + \beta - B\beta\theta^2 = 0$

1次近似では高次項を無視して：

$A + \alpha = 0$ より $\alpha = -A = -\frac{1-\cos\theta}{\theta^2}$
$B + A\alpha + \beta = 0$ より $\beta = -B - A\alpha = -B + A^2$

$A = \frac{1-\cos\theta}{\theta^2}$、$B = \frac{\theta-\sin\theta}{\theta^3}$を用いて計算すると：

\alpha = -\frac{1}{2}, \quad \beta = \frac{1}{\theta^2}\left(1 - \frac{A}{2B}\right)

したがって：

V^{-1} = \boldsymbol{I} - \frac{1}{2}[\boldsymbol{\omega}]_\times + \frac{1}{\theta^2}\left(1 - \frac{A}{2B}\right)[\boldsymbol{\omega}]_\times^2

3.3 実装

💻ソースコードを見てみよう

剛体変換に関する実装：Pose3.h
指数写像の実装：Pose3.cpp gtsam::Pose3::Expmap()
対数写像の実装：Pose3.cpp gtsam::Pose3::Logmap()

⌨実装例

#include <gtsam/geometry/Pose3.h>
#include <gtsam/geometry/Rot3.h>
#include <gtsam/base/Vector.h>
#include <iostream>

int main() {
  using namespace gtsam;

  // 適当なPose3（回転＋並進）
  Pose3 T(Rot3::RzRyRx(0.1, -0.2, 0.3), Point3(1.0, 2.0, 3.0));

  // Pose3 -> se(3)（Vector6: [omega(3), v(3)]）
  Vector6 xi = Pose3::Logmap(T);

  // se(3) -> Pose3
  Pose3 T_recovered = Pose3::Expmap(xi);

  return 0;
}

まとめ

リー代数からリー群への変換は指数写像、リー群からリー代数への変換は対数写像を用いる。
$\mathfrak{so}(3)$ から $SO(3)$ への指数写像はロドリゲスの公式となっている。
最後に、IMU Preintegration on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimationの式(6)まで読めるようになっているか確認することを推奨する。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

[Lie-learning] 第3回 指数写像・対数写像

1. 概要

1.1 指数写像と対数写像について

1.2 SO(2)でデモ

2. SO(3)

2.1 指数写像 (Exponential map)

計算式

式の導出

2.2 対数写像 (Logarithm map)

計算式

式の導出

2.3 実装

3. SE(3)

3.1 指数写像 (Exponential map)

計算式

式の導出

3.2 対数写像 (Logarithm map)

計算式

導出

3.3 実装

まとめ

[Lie-learning] 第3回指数写像・対数写像