はじめに
僕自身まだ深層学習を初めて間もない初心者ですが、偶然図書館で見つけた
「つくりながら学ぶ!深層強化学習 PyTorchによる実践プログラミング 」
という本を読んで深層強化学習に非常に興味を持ちました。
この記事は自分の備忘録として、
「深層強化学習とはどういうものなのか」
をまとめた記事となっています。
強化学習とは
教師あり学習、教師なし学習に並ぶ機械学習の一種であり、簡単に言うと
「人間がHowを教えなくても様々な問題の解決策をみいだすことができる方法」といったものです。
例えば
「子供が自電車に乗れるようになる」ということを例として考えてみます。
このとき子供は、力学の知識を教えてもらったり、youtubeで「自転車 乗り方」と調べて動画から学ぶわけでもありません。
実際に自転車に乗ってみて、何度も失敗して試行錯誤をしながらうまく乗れる方法を見つけます。
強化学習はこの自転車の例のように、対象を支配している物理法則を知らない状態で試行錯誤を繰り返しながら、望ましい制御方法を学ぶ学習方法というわけです。
強化学習の概要
強化学習は下図のようなイメージで説明されます。
これを見てもよくわからないと思うので、「スーパーマリオブラザーズ」を例にして用語の意味から説明していきます。
エージェント(agent)
行動を行う人物または物体を指します
ここでのエージェントは「マリオ」
になります。
状態(state)
エージェントのいる環境の様子
sttでの環境の様子
例)マリオ、クリボーの位置など
行動(action)
エージェントが環境に働きかける行動
attでの行動
例)クリボーを踏む、ファイアボールを放つ
報酬(reward)
環境からエージェントに与えられる評価
rt :tでの環境からの評価
例)コインを獲得、敵を倒すことにより得られるスコア
方策(policy)
エージェントの行動パターン
π(s,a):状態sで行動をとる確率として合わらすことが多い
例)
| マリオの行動 | 選択確率 |
|---|---|
| ジャンプ | 0.3 |
| 進む | 0.1 |
| ファイア | 0.5 |
| 下がる | 0.1 |
収益(return)
報酬の和 Rt
割引率γを導入して未来で得る報酬をどの程度割り引くか調整する
R_t=r_t+γr_{t+1}+γ^2r_{t+2}+γ^3r_{t+3}+...
この割引率γ(0~1)をどのように設定するかで未来の報酬をどれくらい重要視するか決まります。
例えば
・γ=1の時(すべての報酬が同じ大事さ)
R_t=r_t+r_{t+1}+r_{t+2}+r_{t+3}+...
・γ=0.9(未来のことも重視)
R_t=r_t+0.9r_{t+1}+0.81r_{t+2}+0.729r_{t+3}+...
・γ=0(いまを生きる)
R_t=r_t
γはハイパーパラメータで、人が調整しなければなりません。多くの場合は0.995など1に近い値が使われることが多いそうです。
強化学習の目標
さて、これまで強化学習に必須な用語を説明してきましたが、これらを使ってどのように学習するの?と思われた方もいるかもしれません。
それはずばり
報酬の総和、つまり収益を最大化できるように学習を進めていく
というやりかたです。
具体的にはどうやって?となると思うので、これからそのアルゴリズムについて書いていきます。
アルゴリズム
「報酬を最大化する」といっても、上記の式は行動、状態を含んでいないので行動を再現できません。
ではどのようにして、「報酬を最大化」するのかというと
- 価値反復法
- 方策反復
- etc
など様々なアプローチがあります。
以降価値反復法の一種である、Q学習について説明します。
Q学習
Q学習では、行動価値関数(Q関数)を更新してくことで学習を進めていきます。
Q関数とは
状態sで行動aを行ったときの収益を推定する関数
一番簡易的なQ関数の表し方はテーブル方式のものです
| 状態s/行動a | 1.ファイア | 2.ダッシュ |
|---|---|---|
| 1.残り時間が少ない | 1 | 9 |
| 2.クリボーが目の前にいる | 8 | 1 |
| *数字は報酬を表す |
式で表すと
Q(s=1、a=1)=1
Q(s=2、a=1)=8
と、こんな感じになります
Q関数の更新式
Q関数の更新式は
Q(s_t,a_t )=Q(s_t,a_t )+α*(r_{t+1}+γmax_aQ(s_{t+1},a)-Q(s_t,a_t )
と表せます。
αはステップサイズ(学習率)を表します
正直この式の意味は完全に理解していないのですが、こんな感じで更新されるんだー、てくらいの認識でいいと思います。
この更新式を使った更新は以下の通りです。
- Q(s, a) を任意に初期化
- 各エピソードに対し繰り返し:
-
sを初期化
-
エピソードの各ステップに対して繰り返し:
- Q関数と探索を使って、sでの行動aを選択する
- 行動aを取り、r, s' を観測する
- Q(s, a) ← Q(s, a) + α[r + γmaxa′ Q(s', a') - Q(s, a)]
- s ← s';
-
sが終端状態ならば繰り返しを終了
-
テーブルでQ関数を表せない💦汗
しかし、簡単な迷路探索問題では問題ないのですが、ブロック崩しのような複雑なゲーム設定では、actionやstateの組み合わせ数が多すぎて、とてもQテーブルでは試行数が多すぎて実装不可能です。
この「状態変数が多くなると表形式表現の強化学習が困難である」という課題点を解決するためにDeepLearning
を使用します。
DQN
DQNではQ関数を表形式で表現する音をやめ、DNN(ディープ・ニューラルネットワーク)でQ関数を表現(近似)します
ブロック崩しを例にして考えていきます。
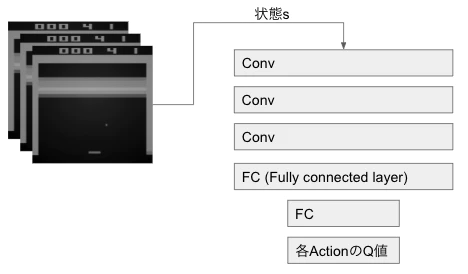
簡単にまとめたのが次の図です
入力としてある瞬間の画像を使い、その画像に対する各ActionのQ値を返します。一枚ごとにNNを回していては遅いため、DQNではすべての行動のQ値をまとめて出すようにしています。
DQNで行われている工夫
しかし上述した手法だけだと、単に線形にQ関数を近似したモデルに精度が負けてしまっていたそうです。
そこでDQNで安定した学習を実現させるために、さまざまな工夫がなされました
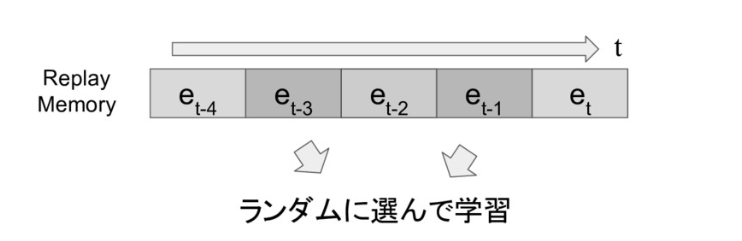
- Experience Replay
メモリに各ステップの内容を保存しておき、メモリから内容をランダムに取り出して、NNに学習させる方法のことです。
時間的に相関が高い内容を連続してNNが学習すると、結合パラメータの学習が安定しづらい、という問題を解決することができます
- Freezing the Target Network(Fixed Target Q-network)
Q学習のアルゴリズムで行動価値関数(Q関数)を更新するためには、次の時刻の状態st+1での価値関数が必要となります。ですがこれら2つを同じQ関数にしているとQ関数の更新が不安定になってしまうという問題が発生します。
この問題を解消するために少し前の別のQ関数を使って計算してあげますというのがFreezing the Target Networkです。

- Clipping Rewards
ゲームによってはスコアのスケールがちがうので、学習率、割引率などを逐一変更しなければなりません。
そこでさまざまなゲームに同じハイパーパラメータで対応するために
負のスコアは-1
正のスコアは+1
で統一してあげます
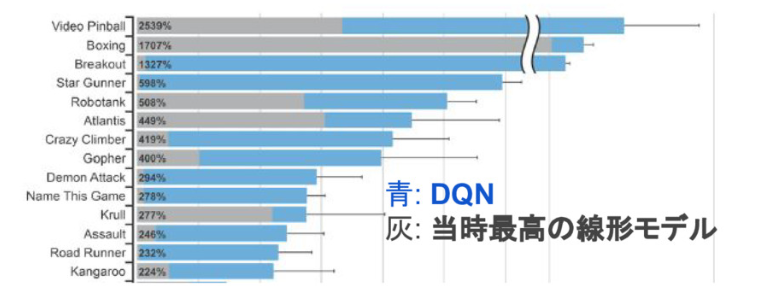
人間を超える
様々な工夫を凝らしてついにDQNは人間のスコアを超えることができました。
最後に
皆さんが思い描いているAI像に一番近いのが深層強化学習によるモデルだと思います。そんなものが自分自身で作れるとおもうとワクワクしますよね
深層強化学習はさらに発展を遂げ、今ではさまざまなモデルが作られています。
いずれそういった発展モデルについての記事も書いてみようとおもっています。
最後まで読んで頂きありがとうございました!!
<参考記事>
趣味の強化学習入門
[深層強化学習の動向 ]
(https://speakerdeck.com/takuseno/survey-of-deep-reinforcement-learning?slide=2)