前回の記事 で書き足りなかったことを少し書くだけです．
ラベルというのは人間が勝手にきめたものなので，教師なしでラベルがきれいにわかれるなんてことは，MNISTならまだしも実際には難しいと思います．
というわけで，前回の記事に100個だけラベルを教えた場合にちゃんとクラスタリングされるのかをみてみたいと思います．
モデル
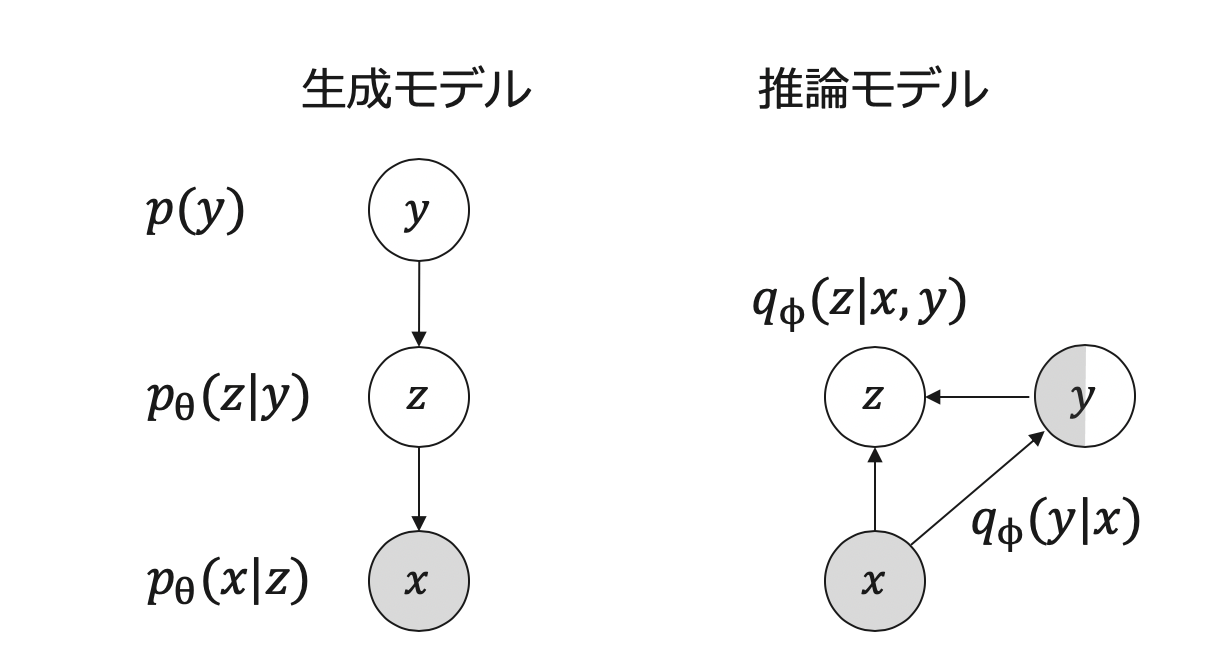
以下が今回のモデルです．
なにが変わったかお気づきでしょうか．
右の推論モデルのyが半分だけグレーになっただけです．
つまり，$q_\phi(y|x)$を教師ありで少しサンプルを使って学習するということです．
もう一つは，$q_\phi(z|x,y)$と$p_\theta(x|z)$使って再構成する項も教師ありサンプルを使って学習に使えそうです．
前回のコードとの差分
コードは雑ですが，1batch分(100個)だけのデータを教師ありとして利用しました．
ロスにクロスエントロピー項を追加し，再構成誤差の項も教師ありサンプルを使って学習します．
alphaの値は自由ですがとりあえず1000にしました．
x_label, y_label = iter(train_loader).next()
x_label = x_label.to(device)
y_label = y_label.to(device)
# クロスエントロピー項
pred = qy_x(x_label)
Xent = F.cross_entropy(pred, y_label, reduction="sum")
# 再構性項
y_label_onehot = torch.eye(K)[y_label].to(device)
z_label = qz_xy(x_label, y_label_onehot)
recon_x_label = px_z(z_label)
recon_loss_label = F.binary_cross_entropy(recon_x_label, x_label, reduction="sum")
# ロスを追加
recon_loss += recon_loss_label*100/60000
loss = recon_loss + kl_cat + kl_gauss*beta + Xent*alpha
結果
訓練の様子
yごとのサンプリング
前回の実験よりも混ざっている数字が少ない
テストデータの潜在変数における配置
前回の実験よりもいい感じにデータがいい感じにわかれている
zの事前分布の可視化
zの事前分布$p_\theta(z|y)$の可視化
