VAEを使った教師なしクラスタリングをやってみたので,自分のための備忘録としてここにメモしておく
VAEを使ったクラスタリング手法は昔からいろいろある[引用文献略].
その中でも最も簡単に実装できてなおかつチューニングも楽そうなものをやってみる.
タスクとしては,まずMNISTの教師なし分類をやってみる.
モデル
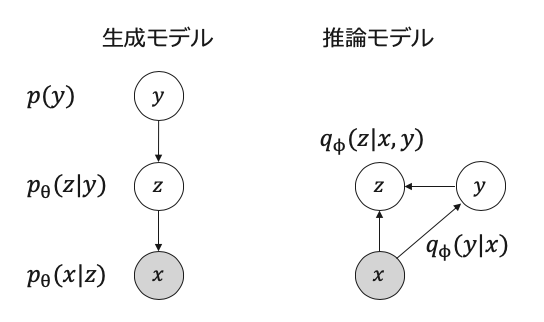
まず,上図のようにモデル化する.
ちなみに,kingmaのM2モデルは教師なしクラスタリングが少しうまく行きにくいとの噂を聞いたのでそれとは生成過程を少し変えている.
ここで,θとφはニューラルネットワークのパラメタ,Kはカテゴリ数
p(y) = \frac{1}{K} \\
p_\theta(z|y) = \mathcal{N}(\mu_\theta(y), \sigma_\theta^2(y)) \\
p_\theta(x|z) = Bern(\mu(z)) \ or \ \mathcal{N}(\mu_\theta(z), \sigma_\theta^2(z)) \\
q_\phi(y|x) = Cat(\pi_\phi(x)) \\
q_\phi(z|x,y) = \mathcal{N}(\mu_\phi(x,y), \sigma_\phi^2(x,y))
これをコードにすると下のようになる.
長いので飛ばしてください.
# 推論モデル
# q(z|x, y)
class Qz_xy(nn.Module):
def __init__(self, z_dim=2, y_dim=10):
super(Qz_xy, self).__init__()
self.z_dim = z_dim
# encode
self.conv_e = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=4, stride=2, padding=1), # 28 ⇒ 14
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
nn.Conv2d(64, 128, kernel_size=4, stride=2, padding=1), # 14 ⇒ 7
nn.BatchNorm2d(128),
nn.LeakyReLU(0.2),
)
self.fc1 = nn.Sequential(
nn.Linear(128 * 7 *7, 40),
)
self.fc2 = nn.Sequential(
nn.Linear(128 * 7 * 7, y_dim),
)
self.fc = nn.Sequential(
nn.Linear(40+y_dim, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 2*self.z_dim),
)
def forward(self, x, y):
x = self.conv_e(x)
x = x.view(-1, 128 * 7 * 7)
x1 = self.fc1(x)
x2 = self.fc2(x)
x = torch.cat([x1, x2*y], dim=1)
x = self.fc(x)
mu = x[:, :self.z_dim]
logvar = x[:, self.z_dim:]
z = self.reparameterize(mu, logvar)
self.mu = mu
self.logvar = logvar
return z
def reparameterize(self, mu, logvar):
if self.training:
std = logvar.mul(0.5).exp_()
eps = std.new(std.size()).normal_()
return eps.mul(std).add_(mu)
else:
return mu
# q(y|x)
class Qy_x(nn.Module):
def __init__(self, y_dim=10):
super(Qy_x, self).__init__()
self.input_height = 28
self.input_width = 28
self.conv1 = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=4, padding=2), # 28x28 ⇒ 14x14
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(2))
self.conv2 = nn.Sequential(
nn.Conv2d(64, 128, kernel_size=4, padding=2), # 14x14 ⇒ 7x7
nn.BatchNorm2d(128),
nn.ReLU(),
nn.MaxPool2d(2))
self.fc = nn.Sequential(
nn.Linear((self.input_height // 4) * (self.input_width // 4) * 128, 256),
nn.Dropout(p=0.4),
nn.ReLU(),
nn.Linear(256, y_dim),
nn.Softmax(dim=1)
)
def forward(self, x):
c1 = self.conv1(x)
c2 = self.conv2(c1)
c2_flat = c2.view(c2.size(0), -1)
out = self.fc(c2_flat)
return out
# p(z|y)
class Pz_y(nn.Module):
def __init__(self, z_dim=2, y_dim=10):
super(Pz_y, self).__init__()
self.z_dim = z_dim
# encode
self.fc = nn.Sequential(
nn.Linear(y_dim, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 2*self.z_dim),
)
def forward(self, y):
x = self.fc(y)
mu = x[:, :self.z_dim]
logvar = x[:, self.z_dim:]
z = self.reparameterize(mu, logvar)
self.mu = mu
self.logvar = logvar
return z
def reparameterize(self, mu, logvar):
if self.training:
std = logvar.mul(0.5).exp_()
eps = std.new(std.size()).normal_()
return eps.mul(std).add_(mu)
else:
return mu
def sample(self, y):
x = self.fc(y)
mu = x[:, :self.z_dim]
logvar = x[:, self.z_dim:]
std = logvar.mul(0.5).exp_()
eps = std.new(std.size()).normal_()
return eps.mul(std).add_(mu)
# p(x|z)
class Px_z(nn.Module):
def __init__(self, z_dim=2):
super(Px_z, self).__init__()
self.z_dim = z_dim
# decode
self.fc = nn.Sequential(
nn.Linear(self.z_dim, 40),
)
self.fc_d = nn.Sequential(
nn.Linear(40, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 128 * 7 * 7),
nn.LeakyReLU(0.2)
)
self.conv_d = nn.Sequential(
nn.ConvTranspose2d(128, 64, kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
nn.ConvTranspose2d(64, 1, kernel_size=4, stride=2, padding=1),
nn.Sigmoid()
)
def forward(self, z):
z = self.fc(z)
h = self.fc_d(z)
h = h.view(-1, 128, 7, 7)
return self.conv_d(h)
z_dim = 2
K = y_dim =10
px_z = Px_z(z_dim=z_dim).to(device)
pz_y = Pz_y(z_dim=z_dim, y_dim=y_dim).to(device)
qy_x = Qy_x(y_dim=y_dim).to(device)
qz_xy = Qz_xy(z_dim=z_dim, y_dim=y_dim).to(device)
これを学習するために,変分下限最大化を利用する.
実際に手を動かすと,VAEっぽい式が出てくる.
L_{ELBO} = \mathbb{E}_{q_\phi(y,z|x)}[\log\frac{p_\theta(x,y,z)}{q_\phi(y,z|x)}]\\
= \mathbb{E}_{q_\phi(y|x)q_\phi(z|x,y)}[\log p_\theta(x|z)] - D_{KL}(q_\phi(y|x))||p(y)) - \mathbb{E}_{q_\phi(y|x)}[D_{KL}(q_\phi(z|x,y)||p_\theta(z|y))]
実際にはこれにマイナスをかけたものを最小化する.
第一項目: 再構成誤差
これは推論モデル$q_\phi(y|x)$を使ってyのサンプリングを行ったあと,$q_\phi(z|x,y)$により,zのサンプリングを行い,生成モデル$p_\theta(x|z)$によってxを生成する.
生成モデルでベルヌイ分布を仮定している場合は実際のxとクロスエントロピーをとる.
また,逆誤差伝播を行うために,リパラメタリゼーションを行う.
yのサンプリングのときは,ギャンベルマックストリックを使っている.
期待値を取るよりも収束が早いらしい[引用略].
第二項目: カテゴリカル分布のKL項
普通のVAEで事後分布を標準正規分布p(z)に近づける項みたいな感じのものがでてきた.
この項には$q_\phi(y|x)$を$p(y)$に近づけてほしいという気持ちが込められている.
p(y)は一様分布としているので,どのxも,どのカテゴリにも属す可能性を高めたいという感じだろうか.
第三項目: ガウス分布のKL項
近似事後分布$q_\phi(z|x,y)$を条件付き事前分布$p_\theta(z|y)$に近づける正則化項である.
この項がないと,xによって推論したyが全く無視されて学習されてしまう感じがあるのでめっちゃ重要.
$q_\phi(y|x)$を使ってyのサンプリングを行うので,ここでもギャンベルマックストリックを使う.
訓練
訓練コードはこんな感じ.
いろいろdefされた関数を使っているが,最後にまとめてかくことにする.
注意してほしいのが,第三項目に関して,beta(定数)倍している.
これはヒューリスティクスで,事前分布にもっと近づいてほしいという僕の気持ちが入っている.
betaVAEとかでも同じようなことしているから許されるだろう.
optimizer = optim.Adam(list(px_z.parameters())+list(pz_y.parameters())
+list(qy_x.parameters())+list(qz_xy.parameters()), lr=1e-3)
epoch_num = 100
for epoch in tqdm(range(epoch_num)):
tau = 0.5 # 温度
beta = 8
# ヒューリスティクス
for x, _ in train_loader:
x = x.to(device)
pi = qy_x(x)
y = gumbel_softmax_sampling(pi, shape=pi.shape, tau=tau)
z = qz_xy(x, y)
recon_x = px_z(z)
recon_loss = F.binary_cross_entropy(recon_x, x, reduction="sum")
pi_prior = (torch.ones(K)/K).to(device)
kl_cat = KL_Cat(pi, pi_prior)
pz_y(y)
kl_gauss = KL_Gauss(qz_xy.mu, qz_xy.logvar, pz_y.mu, pz_y.logvar)
loss = recon_loss + kl_cat + kl_gauss*beta
optimizer.zero_grad()
loss.backward()
optimizer.step()
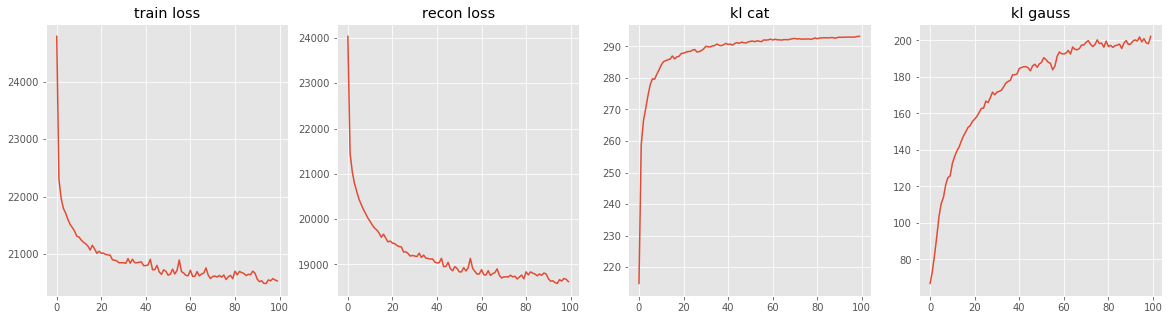
ロス関数は次のようになった.
kl項は全然下がってくれていないが,これは多分問題ない.
実験結果
まず,再構成画像をみてみる.
これができていないとお話にならない.
x, _ = iter(test_loader).next()
x = x.to(device)
y = qy_x(x)
z = qz_xy(x, y)
recon_x = px_z(z)
reconst_plot(x, recon_x)
上: 実際の画像,下: 再構成画像
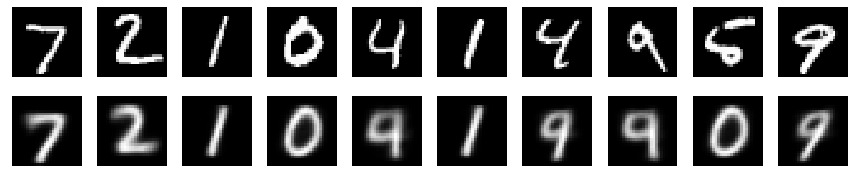
若干怪しいものもあるが,許してほしい.
次に,各y(0~9)を変えたときにどのようなサンプリング画像が生成されるかをみてみる.
つまり$z \sim p_\theta(z|y)$とした後,$x \sim p_\theta(x|z)$とする.
これは,普通のVAEにはできないことである.
plt.figure(figsize=(15, 15))
for i in range(10):
y = torch.eye(K)[np.repeat(i, 10)].to(device)
z = pz_y.sample(y)
x = px_z(z)
for j in range(10):
plt.subplot(10, 10, j+10*i+1)
plt.xticks([])
plt.yticks([])
plt.imshow(x.detach().cpu().numpy()[j][0], cmap=plt.cm.gray)
plt.show()
この結果はおもしろい.
それぞれのyの値から推論されるzに,意味ありげなクラスタが学習されているらしい.
実際にどのようなz空間が学習されているのだろうか.
zは二次元で学習しているのでこれは可視化できる.
まず,$y \sim q_\phi(y|x)$としてyを求めたあと,$z \sim q_\phi(z|x,y)$としてzを求める.
colors = ["r", "g", "b", "y", "pink", "olive", "cyan", "gray", "brown", "purple"]
label = []
latent = []
for x, t in test_loader:
x = x.to(device)
y = qy_x(x)
z = qz_xy(x, y)
latent.extend(z.detach().cpu().numpy())
label.extend(t.numpy())
label = np.array(label)
latent = np.array(latent)
plt.figure(figsize=(10, 10))
for i in range(10):
la = latent[label == i]
plt.scatter(la[:, 0], la[:, 1], s=10, label=i, c=colors[i])
plt.legend(fontsize=12)
plt.show()
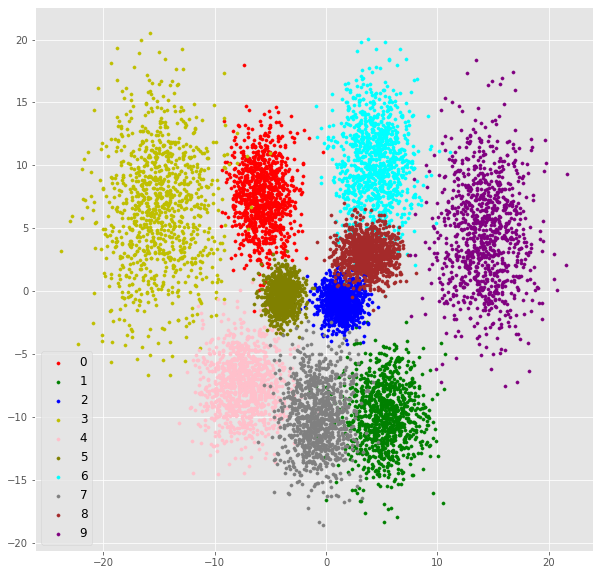
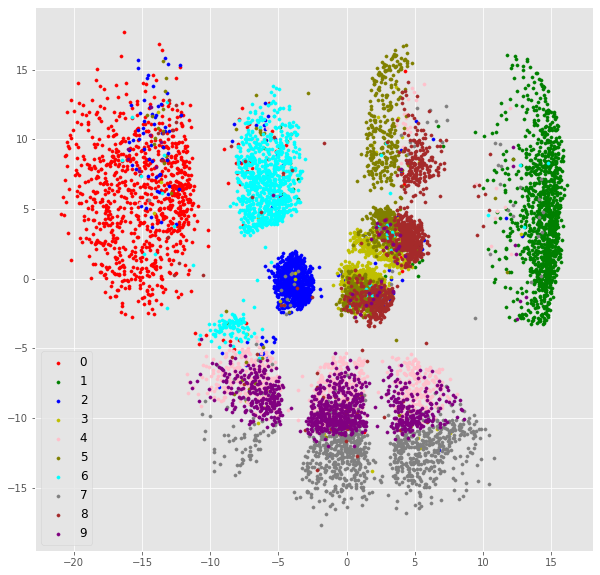
それぞれの点は一つのテスト画像の埋め込みである.
色付けは本物のラベルの色をつけた.
実際にはちゃんとクラスタごとに色がわかれていると良いクラスタリング結果ということになる.
x空間のデータをサンプルしたものからもわかるように,4,7,9や5,8が混ざってしまっている.
ついでに,$p_\theta(z|y)$で得られる空間も図示する.
latent = []
label = []
for i in range(10):
t = np.repeat(i, 1000)
y = torch.eye(K)[t].to(device)
z = pz_y.sample(y)
latent.extend(z.detach().cpu().numpy())
label.extend(t)
label = np.array(label)
latent = np.array(latent)
plt.figure(figsize=(10, 10))
for i in range(10):
la = latent[label == i]
plt.scatter(la[:, 0], la[:, 1], s=10, label=i)
plt.legend()
plt.show()
なるほど,第三項はこういう分布に近づけたかったのか,ということがわかる.
betaを大きくしたおかげでだいぶ近づいている.
その他実験
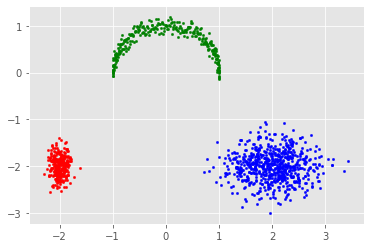
詳細は省くが,低次元のデータに関しても同じようなことが行える
学習した$q_\phi(y|x)$を使えばクラスタリングができる
pred = []
for i in range(M):
x = test_X[batch_size*i:batch_size*(i+1)].to(device)
y = qy_x(x).argmax(1)
pred.extend(y.detach().cpu().numpy())
pred = np.array(pred)
for i in range(y_dim):
plt.scatter(toy[pred==i][:, 0], toy[pred==i][:, 1], s=5, c=["r", "g", "b"][i])
plt.show()
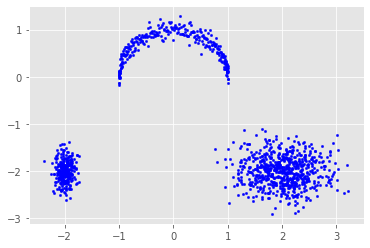
また,生成モデルなので,$p_\theta(z|y), p_\theta(x|z)$を使ってサンプリングもできる
for i in range(y_dim):
y = torch.eye(K)[np.repeat(i, 500)].to(device)
z = pz_y.sample(y)
x = px_z(z).detach().cpu().numpy()
plt.scatter(x[:, 0], x[:,1], s=5)
plt.show()
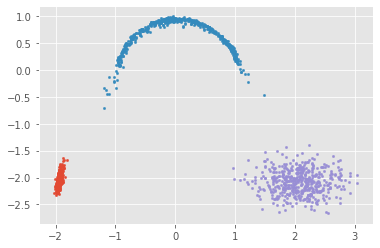
ちなみにデコーダの分布はこの場合ガウス分布で,分散は固定した.
というか分散を推定するようにすると安定しない...
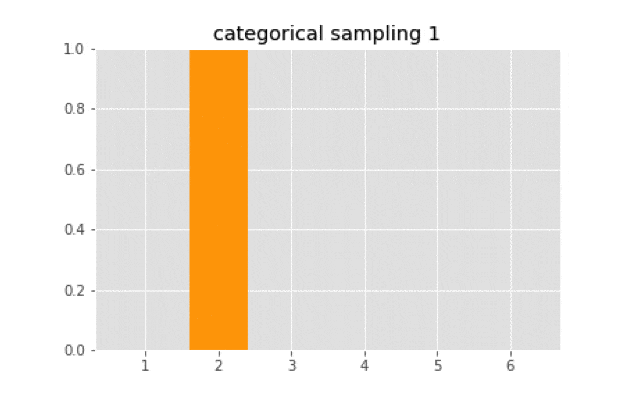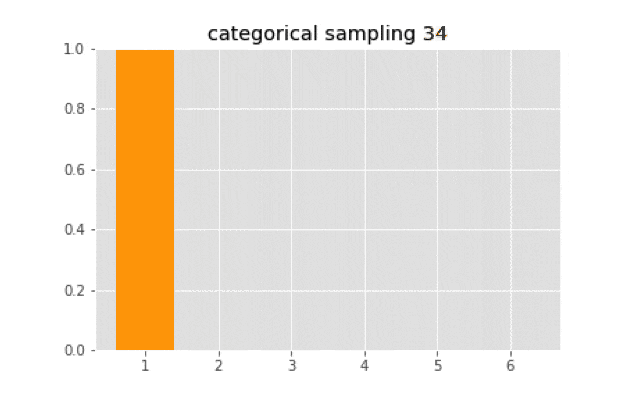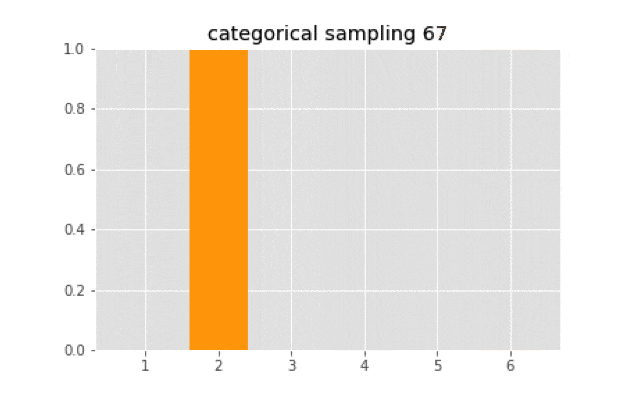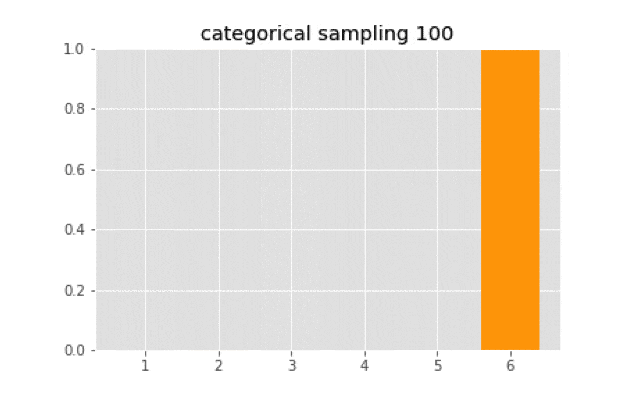
ソフトマックスのサンプリングについて
def sample_gumbel(shape, eps=1e-20):
U = torch.rand(shape)
return -torch.log(-torch.log(U+eps))
def gumbel_softmax_sampling(pi, shape, tau, eps=1e-20):
log_pi = torch.log(pi + eps)
g = sample_gumbel(shape).to(device)
y = F.softmax((log_pi + g)/tau, dim=1)
return y
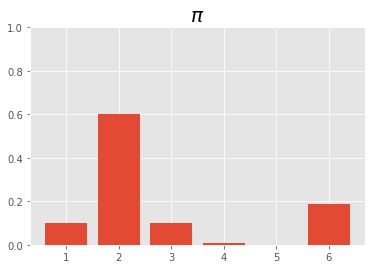
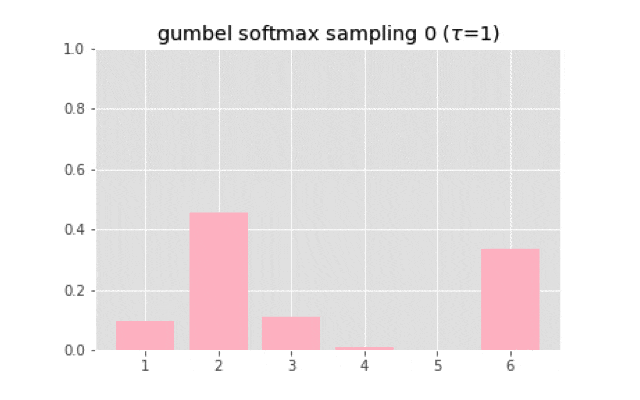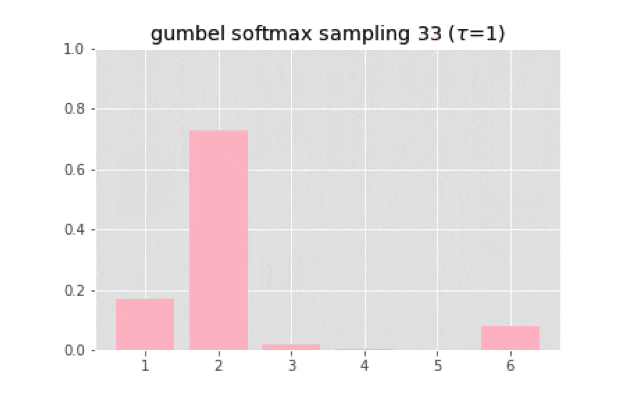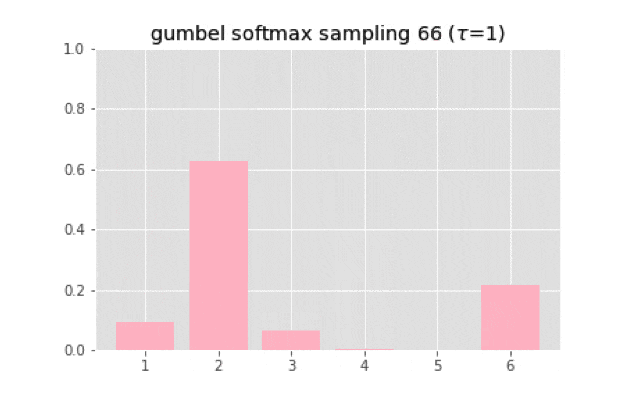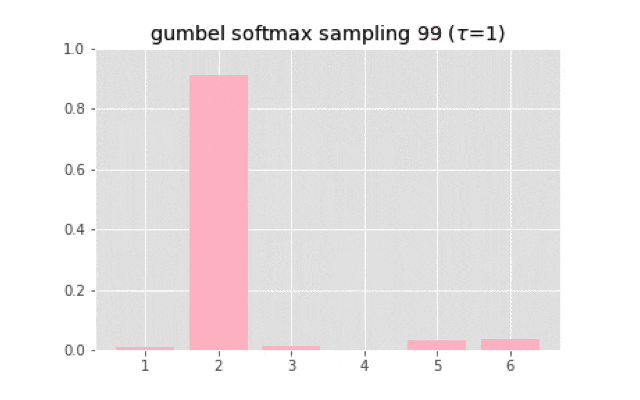
このサイコロを100回転がすと,出目は次のようになる.
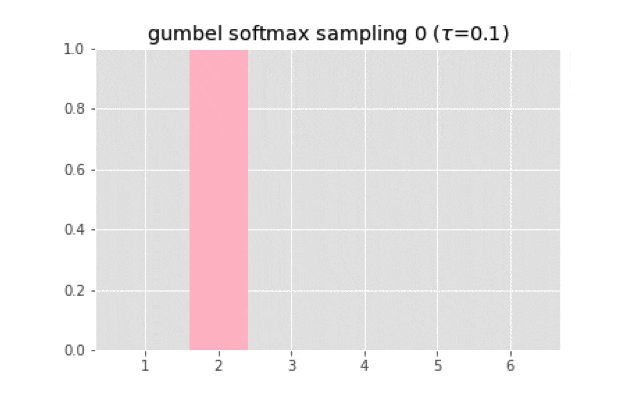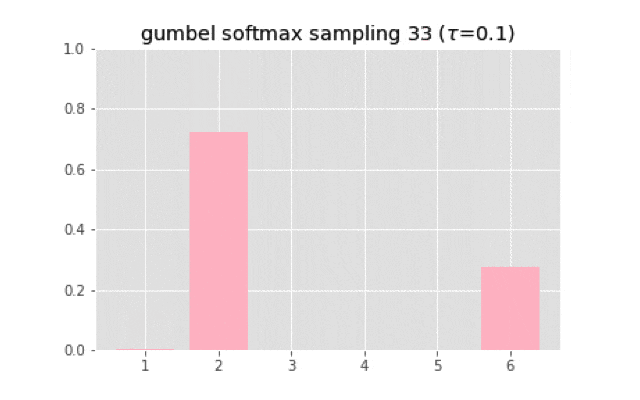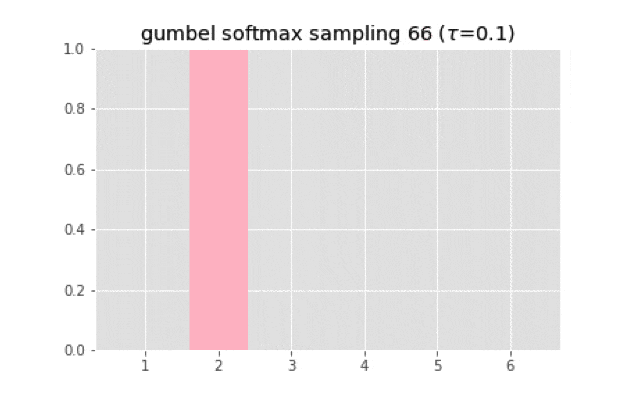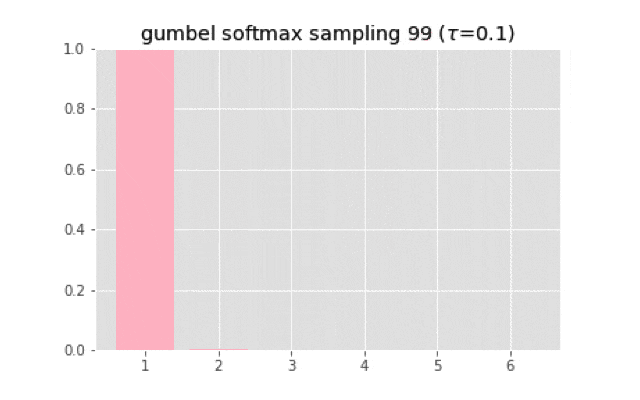
これだとサンプリングしたときに勾配を取る方法がないので,ソフトマックスサンプリングを行う.
上のコードを使って実装すると,次のようなサンプリングになる.
温度が大きくなると一様分布に近づいていく.
もう少し詳しい説明は
https://www.slideshare.net/ssuser9eb780/categorical-reparameterization-with-gumbel-softmax
に昔書いていたことを思い出した.
その他コード
KL項計算用
def KL_Cat(q, p, eps=1e-20):
return (q * torch.log(q+eps) - q * torch.log(p+eps)).sum()
def KL_Gauss(mu1, logvar1, mu2, logvar2):
return -0.5 * torch.sum(1 + logvar1 - logvar2 - logvar1.exp()/logvar2.exp()-(mu2-mu1)**2/logvar2.exp())
可視化用
def reconst_plot(x, recon_x):
plt.figure(figsize=(15, 3))
for i in range(10):
plt.subplot(2, 10, i+1)
plt.xticks([])
plt.yticks([])
plt.imshow(x.detach().cpu().numpy()[i][0], cmap=plt.cm.gray)
plt.subplot(2, 10, i+11)
plt.xticks([])
plt.yticks([])
plt.imshow(recon_x.detach().cpu().numpy()[i][0], cmap=plt.cm.gray)
plt.show()
def sample_plot(x):
plt.figure(figsize=(15, 3))
for i in range(10):
plt.subplot(1, 10, i+1)
plt.xticks([])
plt.yticks([])
plt.imshow(x.detach().cpu().numpy()[i][0], cmap=plt.cm.gray)
plt.show()