記事を書いた理由
Oracle PGXやNeo4jなどといったGraph DBの最短経路クエリについて調べているうちに、最短経路を取得する方法には以下の2つがあることを発見しました。
- クエリ内で最短経路を取得する
- 最短経路計算をするアルゴリズムを呼び出す
Neo4jで最短経路計算をするとき、この2つの方法をどのように使い分けるべきかをまとめてみました。
前提:テストデータの取得
以下のクエリを実行し、テストデータの作成および確認をします。
(こちらの記事も参考にしてください。)
LOAD CSV WITH HEADERS FROM "https://gist.githubusercontent.com/lassewesth/634281cced11147432cf232a2c36e080/raw/1ed1f4fe4ca4c8092bbc8557addd1e5d87316833/eroads.csv" AS row
RETURN row
LIMIT 10
CREATE CONSTRAINT ON (p:Place)
ASSERT p.name IS UNIQUE
USING PERIODIC COMMIT 1000
LOAD CSV WITH HEADERS FROM "https://gist.githubusercontent.com/lassewesth/634281cced11147432cf232a2c36e080/raw/1ed1f4fe4ca4c8092bbc8557addd1e5d87316833/eroads.csv"
AS row
MERGE (origin:Place {name: row.origin_reference_place})
SET origin.countryCode = row.origin_country_code
MERGE (destination:Place {name: row.destination_reference_place})
SET destination.countryCode = row.destination_country_code
MERGE (origin)-[eroad:EROAD {road_number: row.road_number}]->(destination)
SET eroad.distance = toInteger(row.distance), eroad.watercrossing = row.watercrossing
ホップ数のみを考慮する場合:クエリ内で最短経路を取得する
エッジの重みを考慮せず、単純にノードとノードのホップ数のみを考慮する場合は、クエリ内で最短経路を取得します。
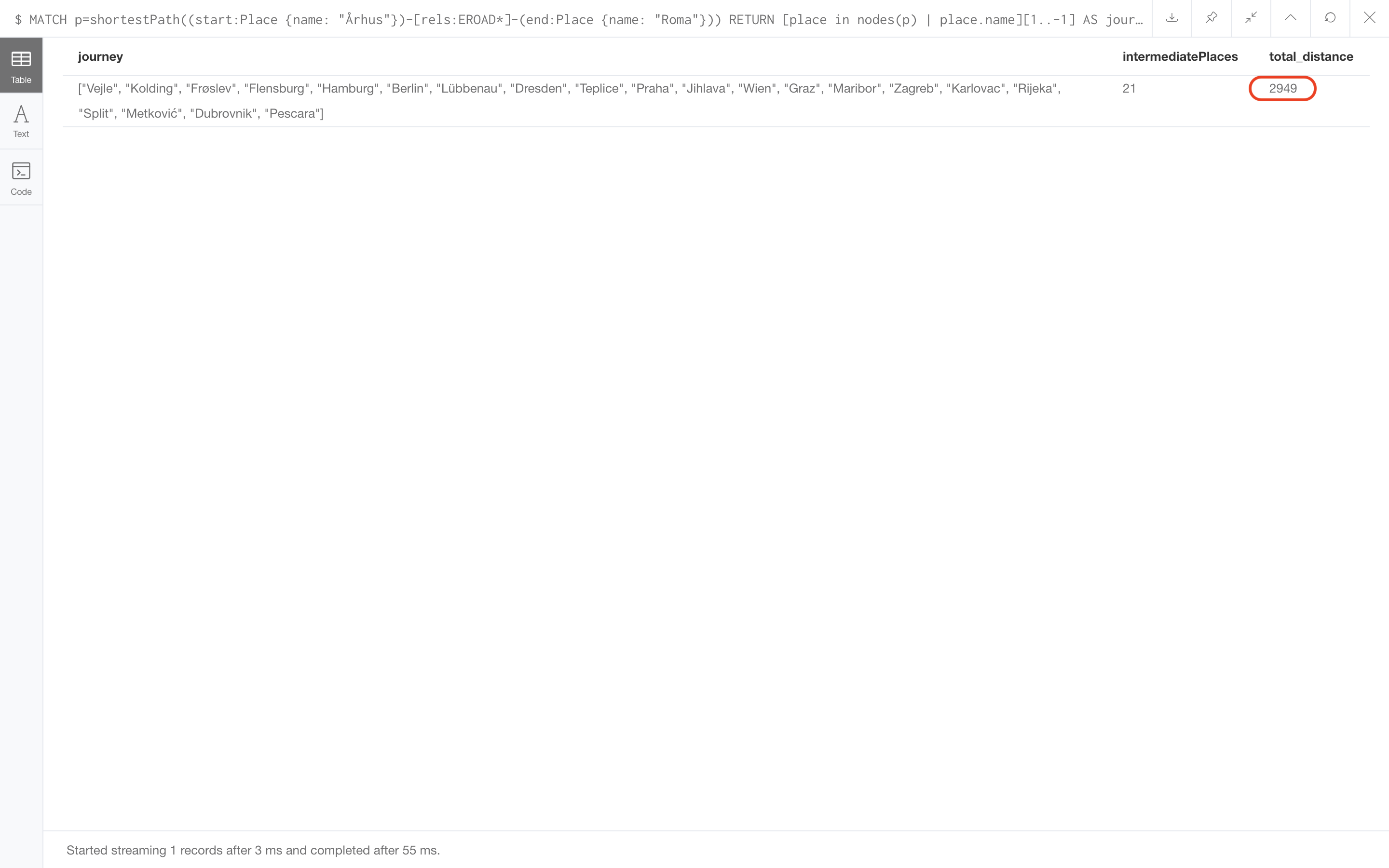
MATCH p=shortestPath((start:Place {name: "Århus"})-[rels:EROAD*]-(end:Place {name: "Roma"}))
RETURN [place in nodes(p) | place.name][1..-1] AS journey,
length(nodes(p)[1..-1]) AS intermediatePlaces,
reduce(s = 0, r in rels | s + r.distance) AS total_distance
エッジの重みを考慮する場合:アルゴリズムを呼び出す
エッジの重みを考慮し、重みの総和が最小になる経路を求めたい場合は、適切なアルゴリズムを呼び出します。
MATCH (start:Place{name:"Århus"}), (finish:Place{name:"Roma"})
CALL algo.shortestPath.stream(start, finish, "distance")
YIELD nodeId, cost
MATCH (n) WHERE id(n)=nodeId
return n.name, cost
結果は以下のようになります。
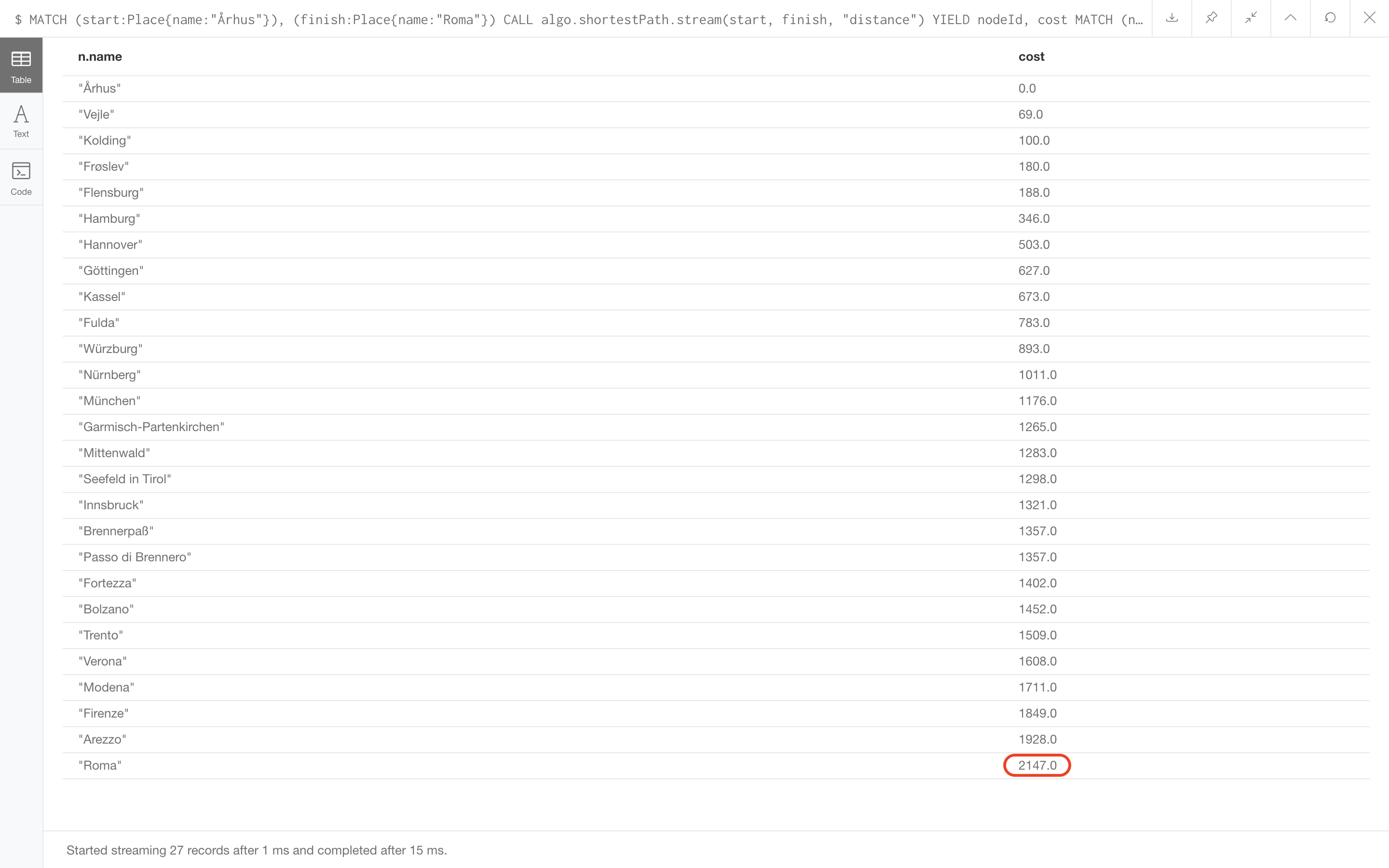
先ほどのエッジの重みを考慮しない、最小ホップ数を持つ経路のコストと比べると、コストの総和が小さくなっているのがわかります。
この裏側では、ダイクストラ法というアルゴリズムが動いています。
補足:ダイクストラ法とは
ダイクストラ法とは、エッジの重みが全て0以上の場合、ある一つの始点からの最短経路を求めるのに最適なアルゴリズムのことです。
ダイクストラ法(だいくすとらほう、英: Dijkstra's algorithm)はグラフ理論における辺の重みが非負数の場合の単一始点最短経路問題を解くための最良優先探索によるアルゴリズムである。
Wikipediaより引用
ダイクストラ法以外で最短経路を求めたい場合:適切なアルゴリズムを呼び出す
上記のように、ダイクストラ法では、(全てのエッジの重みが0以上の場合グラフにおける)最短経路を求めることができました。
しかし、求めたい経路が最短経路以外の経路である場合、ダイクストラ法以外のアルゴリズムを使う必要があります。
例:ÅrhusからRomaまでの3番目に短い経路を求めたい場合
私たちがカーナビを使用する時、いくつかのルートが表示されますよね。例えば、「最短経路上の道路では渋滞が発生しているので、2番目に短い迂回ルートで目的地まで向かう」といった場合、最短経路以外の経路(2番目に短い経路)も求めておく必要があります。(カーナビでの経路探索は、こちらの論文に詳しく書かれています。)
この時に使用するアルゴリズムは、Yen's algorithmです。Yen's algorithmとは、K番目(ある文脈では1~K番目)に短いパスを見つけてくれるアルゴリズムです。詳しい計算の流れはこちらの記事に書いてあります。
実際にNeo4jで試してみます。
MATCH (start:Place{name:'Århus'}), (end:Place{name:'Roma'})
CALL algo.kShortestPaths.stream(start, end, 3, 'cost', {})
YIELD index, nodeIds, costs
RETURN [node in algo.getNodesById(nodeIds) | node.name] AS places,
costs,
reduce(acc = 0.0, cost in costs | acc + cost) AS totalCost
結果は以下のようになります。

このように、アルゴリズム呼び出し時に指定した数字k(ここでは3)番目に短い経路を求めることができます。
Yen's algorithmを呼び出す時、デフォルトではパスを返すことはありませんが、引数にpath: trueを渡してあげると、パスで結果を返してくれます。
MATCH (start:Place{name:'Århus'}), (end:Place{name:'Roma'})
CALL algo.kShortestPaths.stream(start, end, 3, 'cost', {path: true})
YIELD path
RETURN path
LIMIT 3

(パスで結果を返してくれるのですが、経路の長さを直感的に判断できないので、若干わかりづらいですね笑)
蛇足:Yen's Algorithmで最短経路を求めてみた
上記のように、Yen's AlgorithmはK番目(ある文脈では1~K番目)に短いパスを見つけてくれるアルゴリズムでした。
それでは、K=1の場合、最短経路を求めることができるのではないかと考え、実行してみました。
MATCH (start:Place{name:'Århus'}), (end:Place{name:'Roma'})
CALL algo.kShortestPaths.stream(start, end, 1, 'cost', {})
YIELD index, nodeIds, costs
RETURN [node in algo.getNodesById(nodeIds) | node.name] AS places,
costs,
reduce(acc = 0.0, cost in costs | acc + cost) AS totalCost

このように、Yen's Algorithmでも最短経路を求めることができました。
しかし、なぜ最短経路を求める際は、Yen's Algorithmを使用しないのでしょうか?
その理由は、計算量にありました。
Yen's Algorithmの大まかな流れを以下に示します。
- まず最短経路をダイクストラ法で求める。
- 最短経路から分岐した経路(deviation path)を計算する。
Our implementation uses Dijkstra algorithm to find the shortest path and then proceeds to find k-1 deviations of the shortest paths.
Neo4jの公式サイトより引用
まず、ダイクストラ法の計算量はO(V²)です。
Yen's Algorithmの場合は、(エッジの重みが全て非負の場合)ダイクストラ法に加えて第二最短経路、第三最短経路…と計算していくので、直感的に計算量が大きくなることがわかります(正確にはO(KV³))。
最短経路のみを求める場合であれば、計算量の少ないダイクストラ法を用いる方が効率的ですね。
この他にも、Neo4jには様々なアルゴリズムが実装されています。詳しく知りたい方は、こちらをご覧ください。