K Shortest Path Problem とは, K番目(ある文脈では1~K番目)に短いパスを見つける問題です. 色々バリエーションがあるみたいですが, 今回は多重有向グラフについて始点と終点を固定した上でK shortest path problelmを解く方法として Yen の アルゴリズムを紹介します[1].
このアルゴリズムは, 負の枝があっても大丈夫ですが, 負のループがあると機能しません.
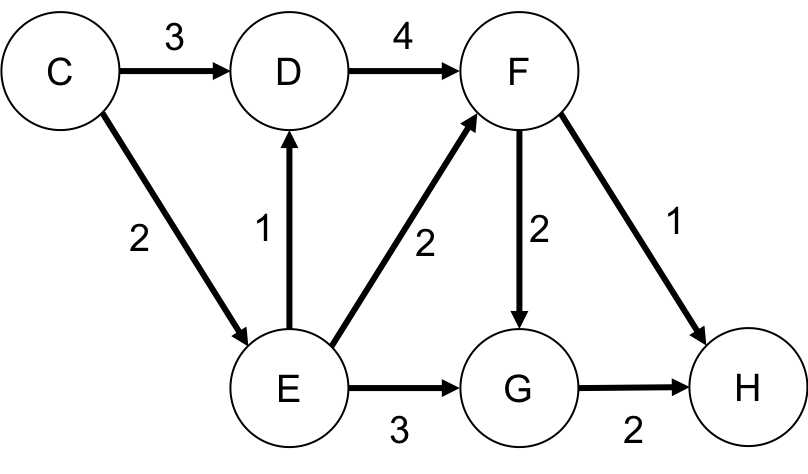
さて, そのYenのalgorithmを英語版Wikiのグラフを用いて簡単に説明したいと思います. **始点はC**で**終点はH**とします. 厳密なアルゴリズムではなく, 直感的に理解できようにその流れを説明します. おそらくアルゴリズム自体はそんなに難しくないはずです.
まずは第1~K最短路を格納する**配列A**と 第k最短路の候補を格納する**配列B**を用意します. Bには優先度つきキューを用いることで計算量を削減することができます. これからの説明では配列Bはキューとして扱います.
上のグラフの第4最短路まで求めてみましょう.
第1最短路
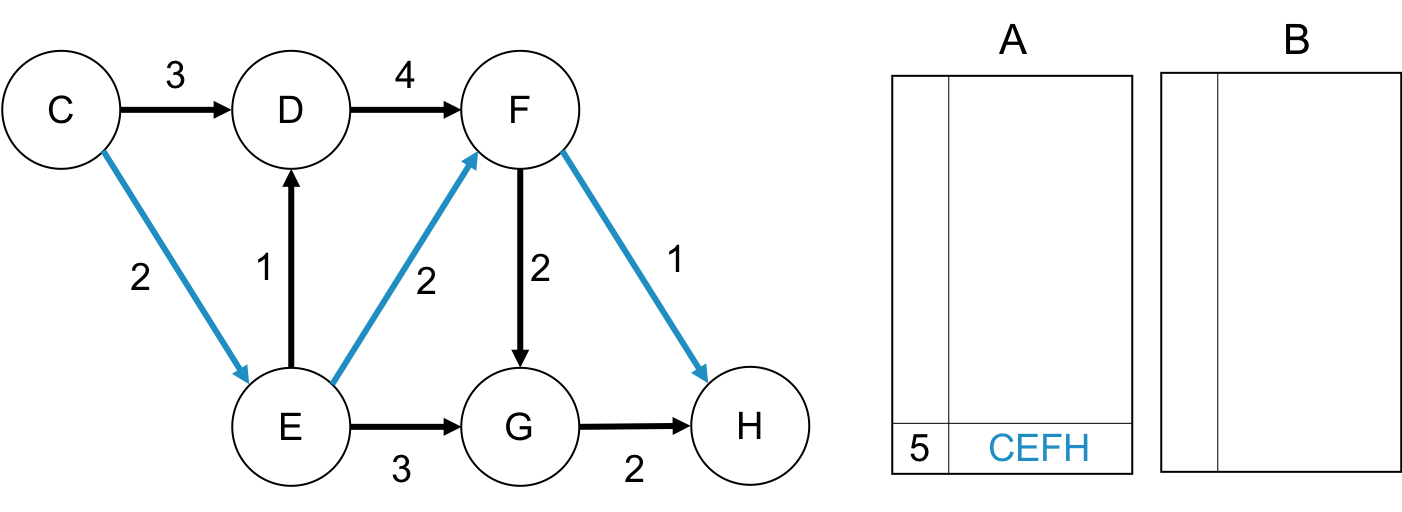
さて, 第1最短路の導出は, Dijkstra法やグラフが負の枝を含む場合はBellman–Ford法を用いて行います.
そしてそれを配列Aに格納します.
第2最短路
第2最短路ですが, (当たり前ですが)これは第1最短路とは異なるパスであるため
パスの始点から考えたときにどこかのタイミングで第1最短路とは別の道を歩むことになります. (論文中では分岐以降のパスをdeviation(偏差) pathと呼んでいます.) パスが分岐する点をspur node, 始点からsqur nodeまでをsqur rootと定めます. 以下のようにspur nodeの位置で場合分けを行います.
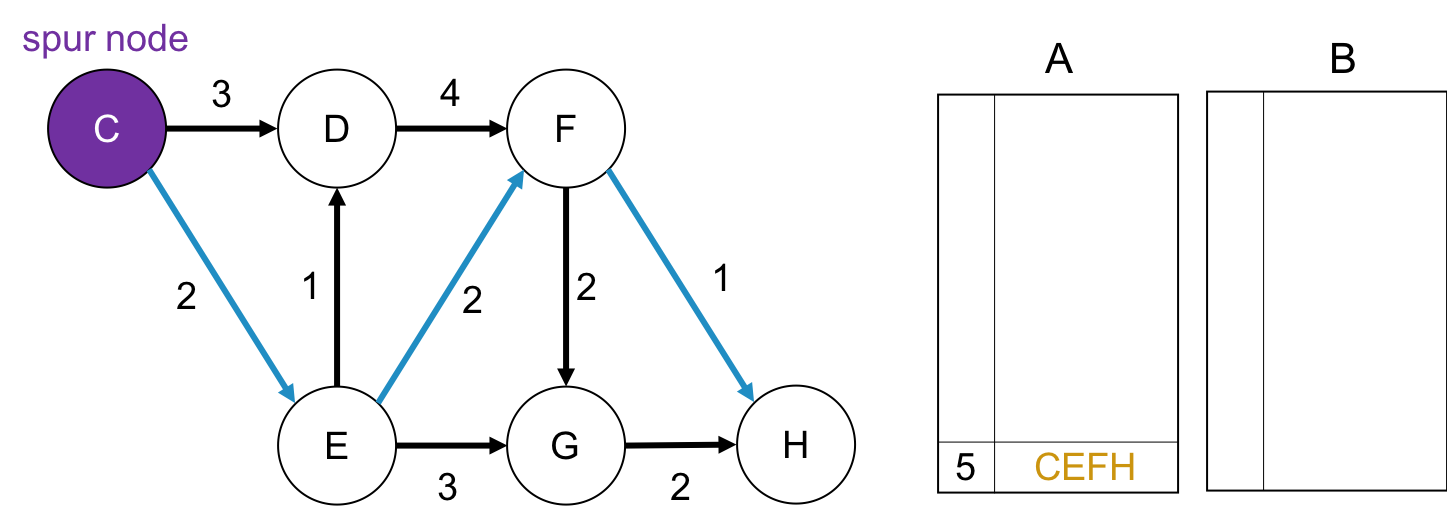
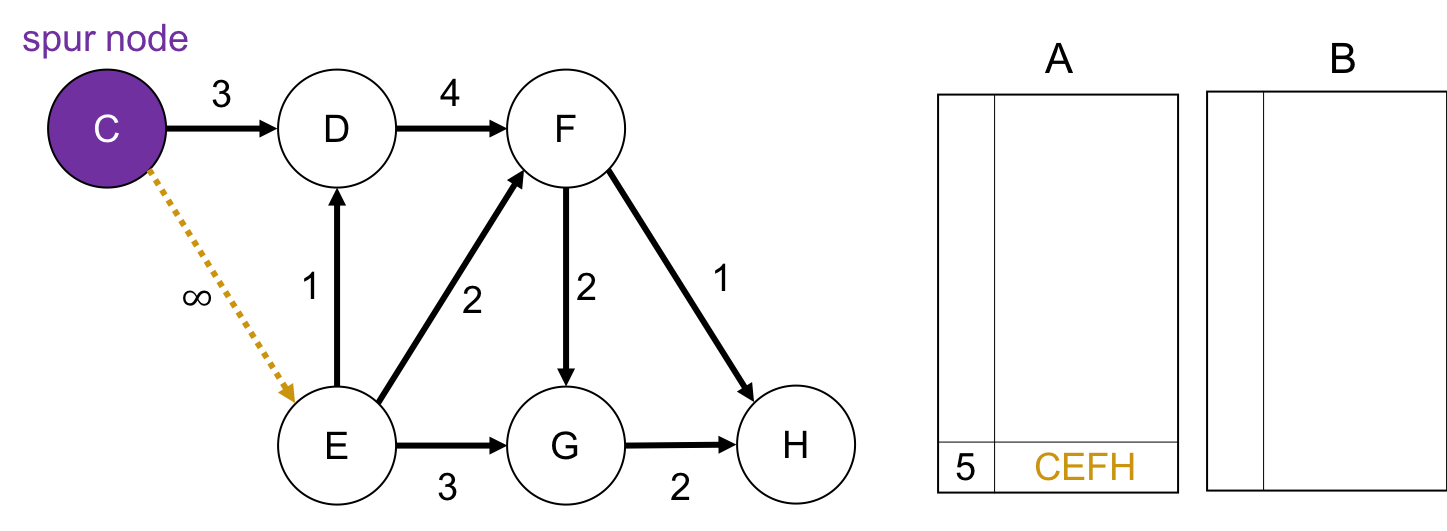
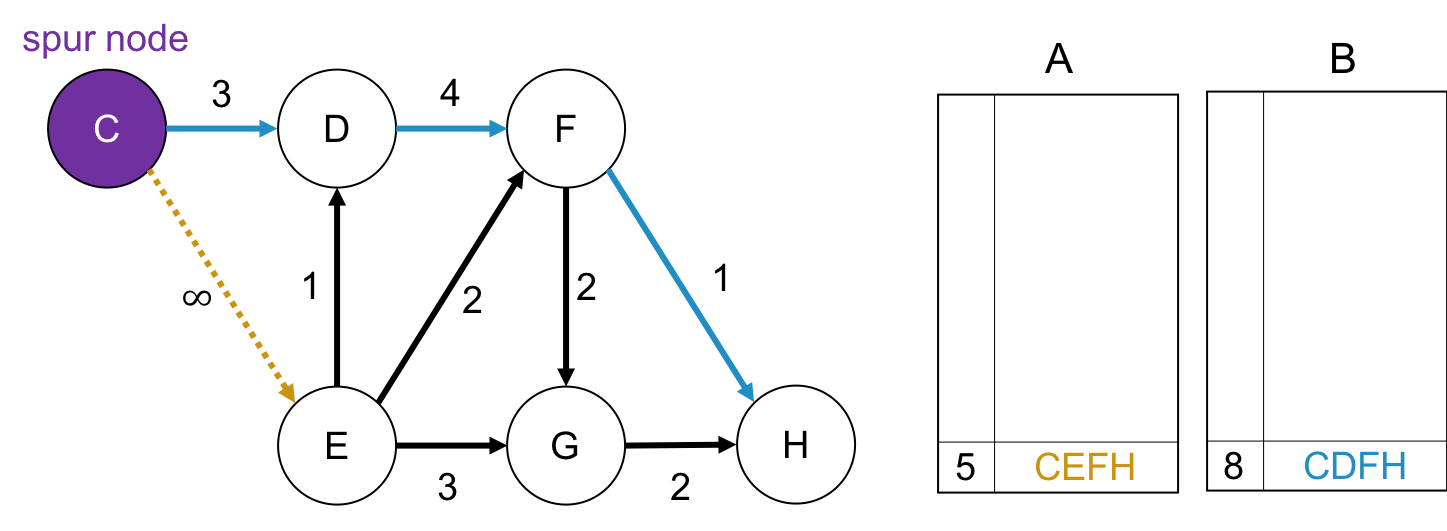
spur node が Cの場合
初っ端から第1最短路とは別の道を歩みます. なので, $C \rightarrow E$ の枝をパスが通ることがないように, 枝の重みを$+\infty$にする, もしくは枝自体を削除します. このとき squr root は $C$です.
そして, spur nodeから終点の$H$までの最短路を求め, それをBに格納します。
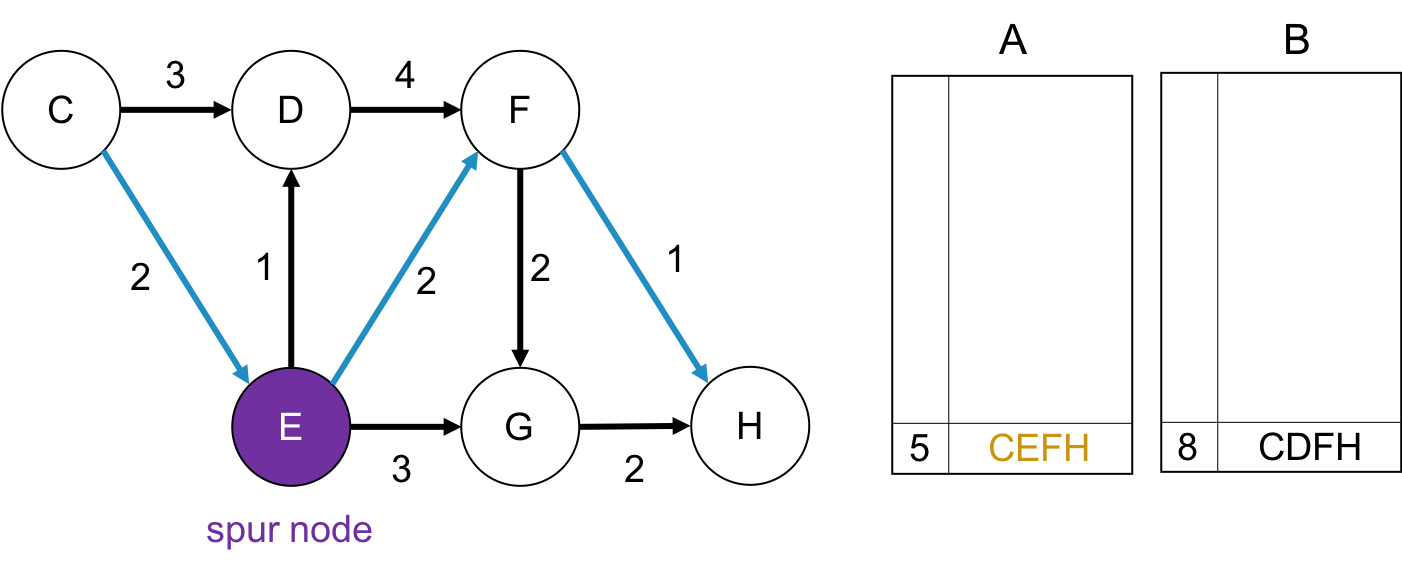
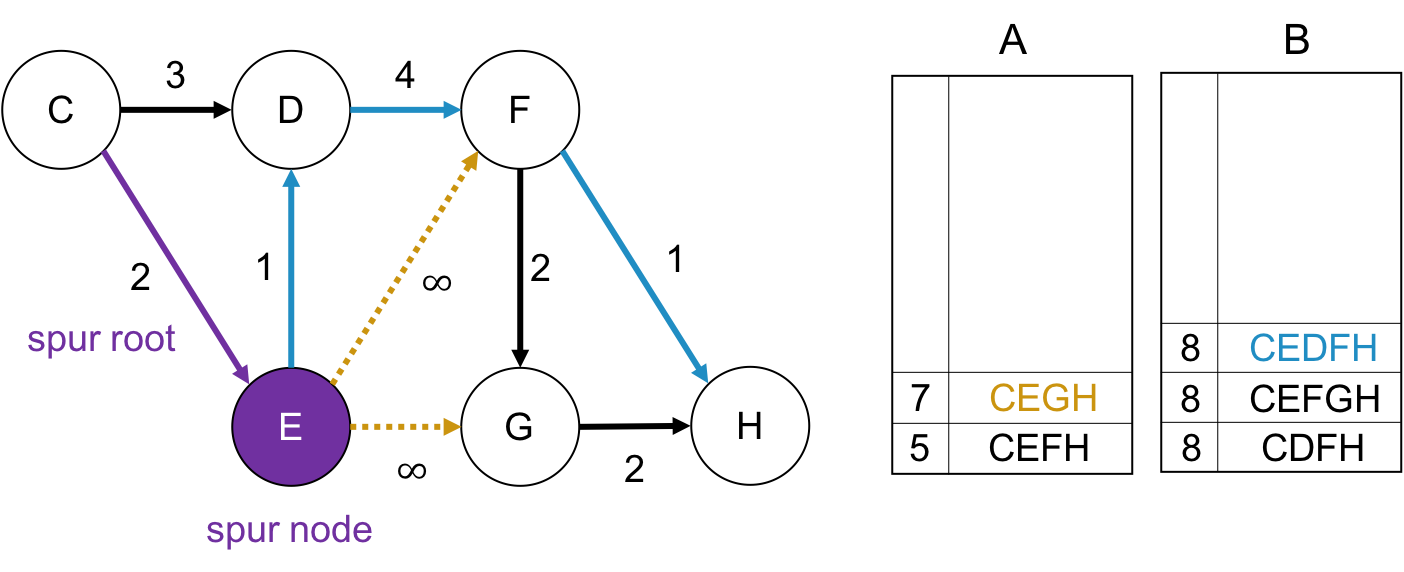
spur node が Eの場合
spur nodeがEの場合も同様に処理します.
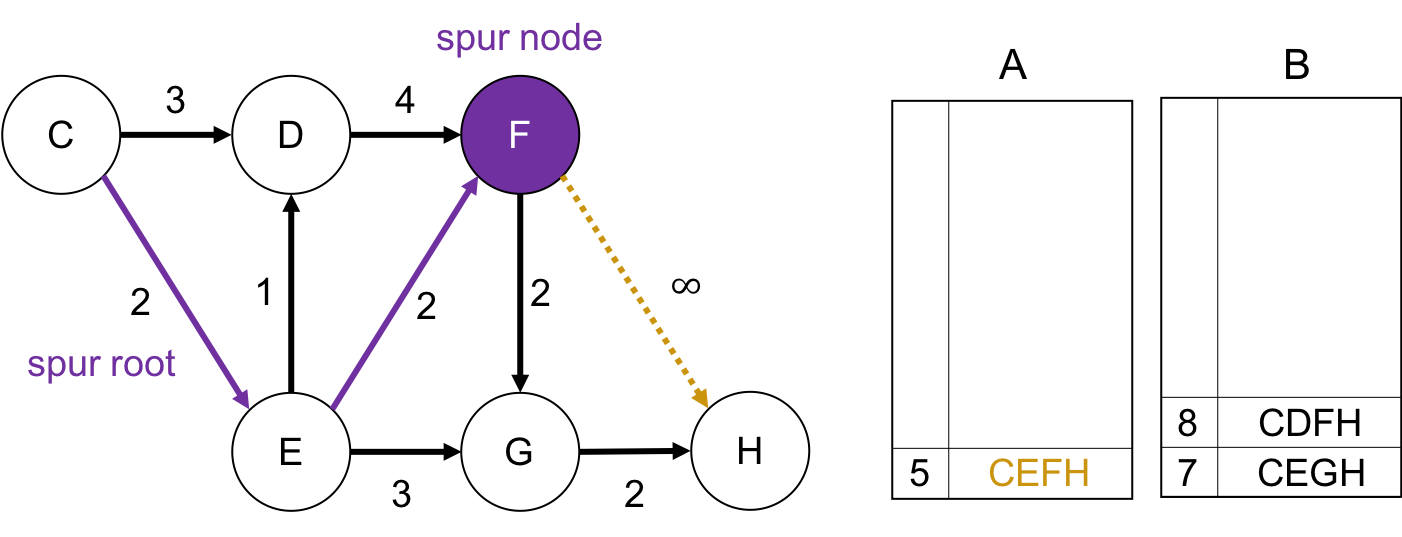
$C \rightarrow E$をspur rootとして, $E \rightarrow F$の枝をパスが通れないようにします. そしてEから終点$H$までの最短路を求めて, それとspur rootを合わせて始点から終点までのパスとして, それをBに格納します. この場合は$CFGH$ですね.
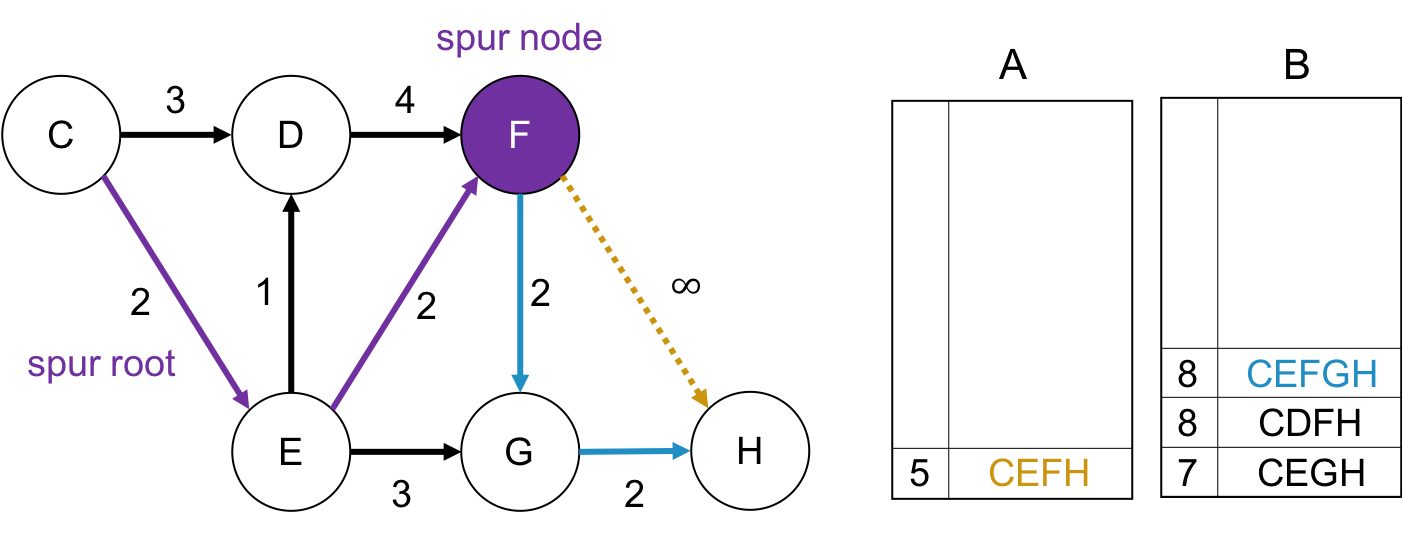
spur node が Fの場合
同様です.
第2最短路の取り出し
そして, Bに格納されたパスの中から, もっともパス長が短いものを取り出してAに移します. それが第2最短路です.
第3最短路
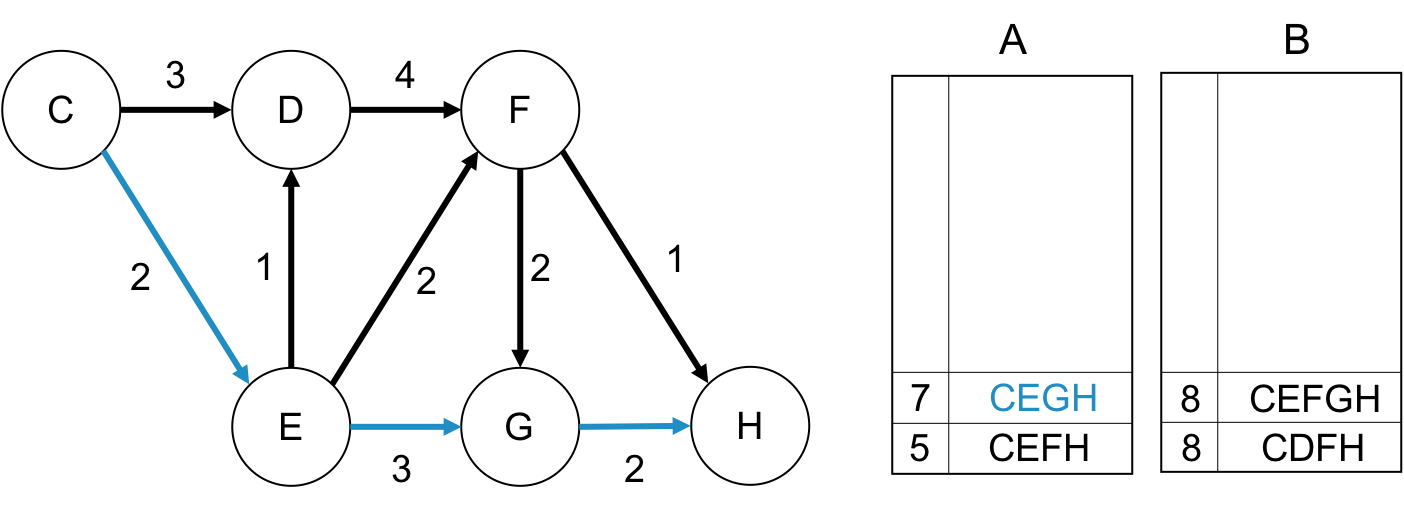
次は第2最短路を基準に, deviation path をBに格納していきます. squr node によって, squr rootが決まりますが, すでに求められている第1~k最短路のなかでsqur rootが含まれているものを探し, squr rootの次の枝の重みを$\infty$, もしくは枝ごと削除します.
spur node が Cの場合
このとき, squr root は$C$ですが, これは第1最短路に含まれるので, $C \rightarrow E$が通れなくなります. これより最短路を求めると, $CDFH$が求まりますがこれはすでにBに格納されているため, 何もしません.
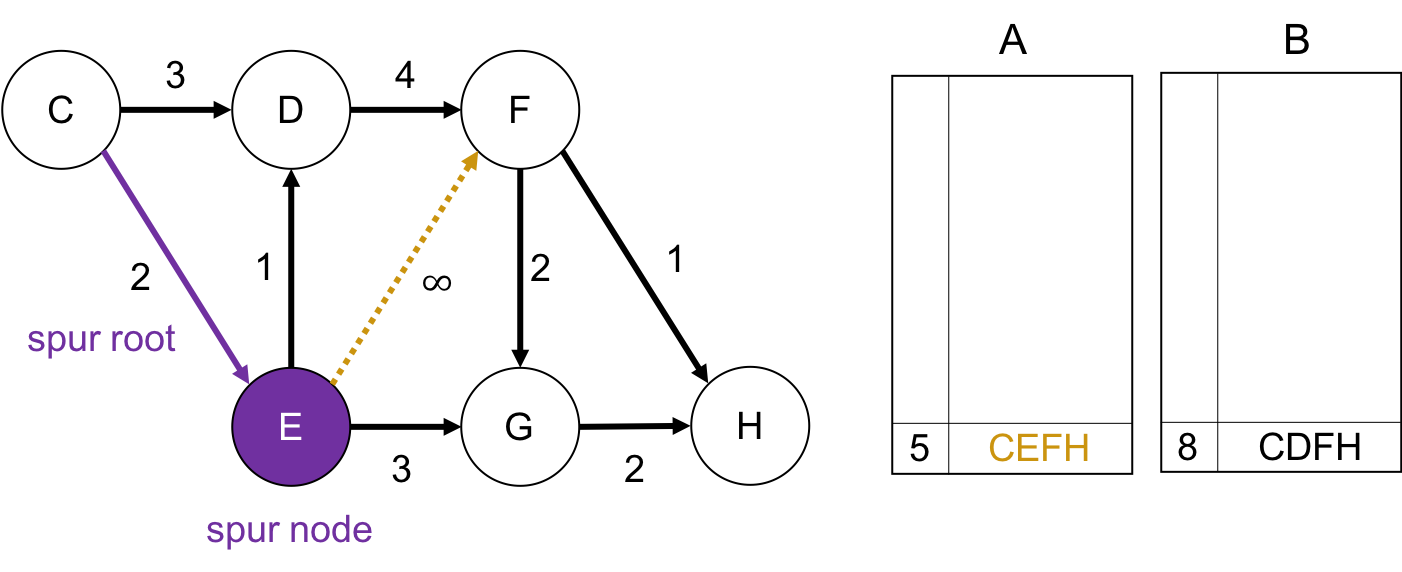
spur node が Eの場合
このとき, squr root は$CE$ですが, これは第1, 2最短路共に含まれるので, $E \rightarrow F$, $E \rightarrow G$が通れなくなります.
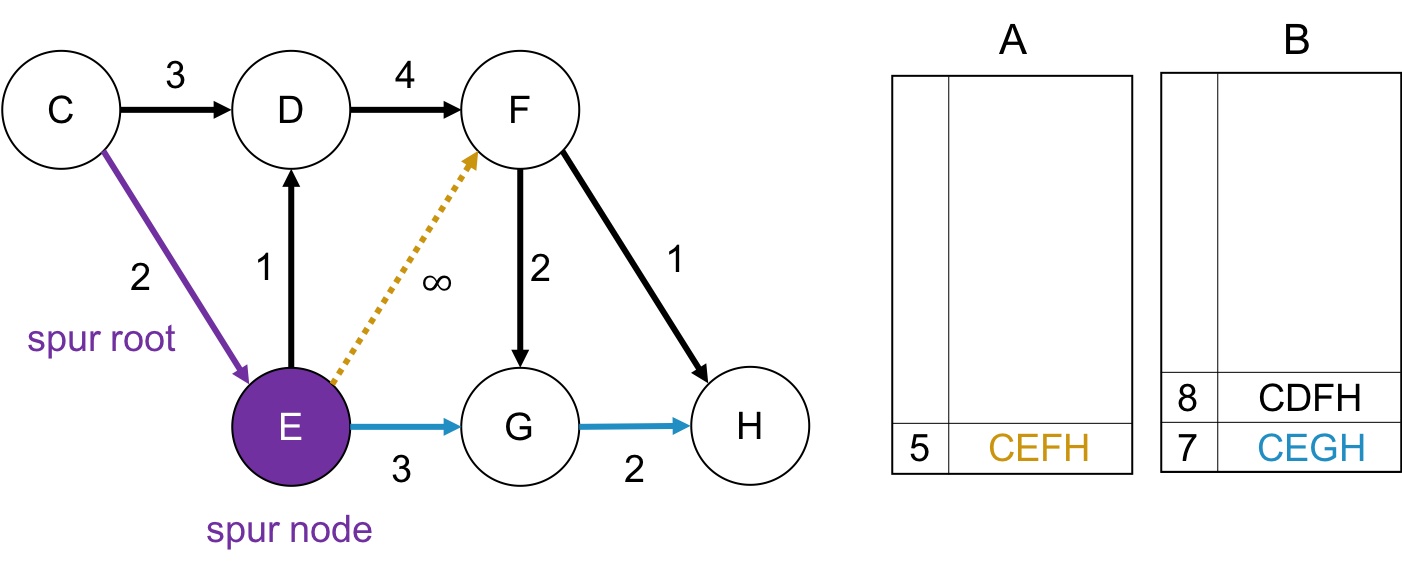
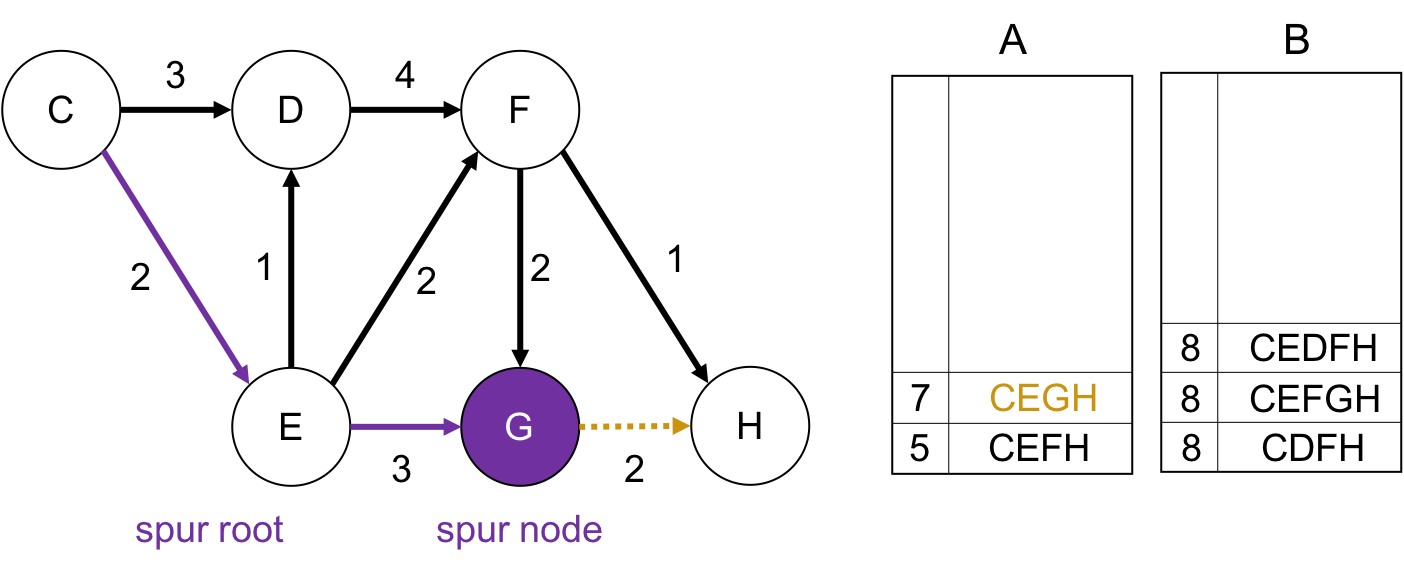
spur node が Gの場合
squr root は$CEG$なので, $G \rightarrow H$が通れなくなります. このとき squr nodeから終点までのパスがないため, 何もしません.
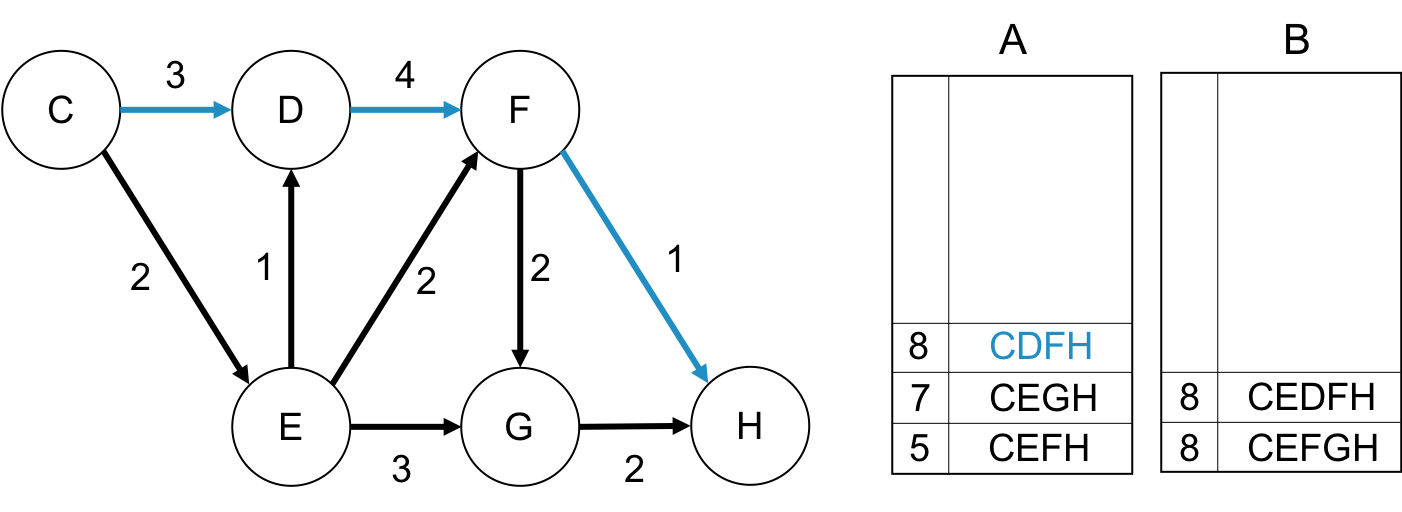
第3最短路の取り出し
第4最短路
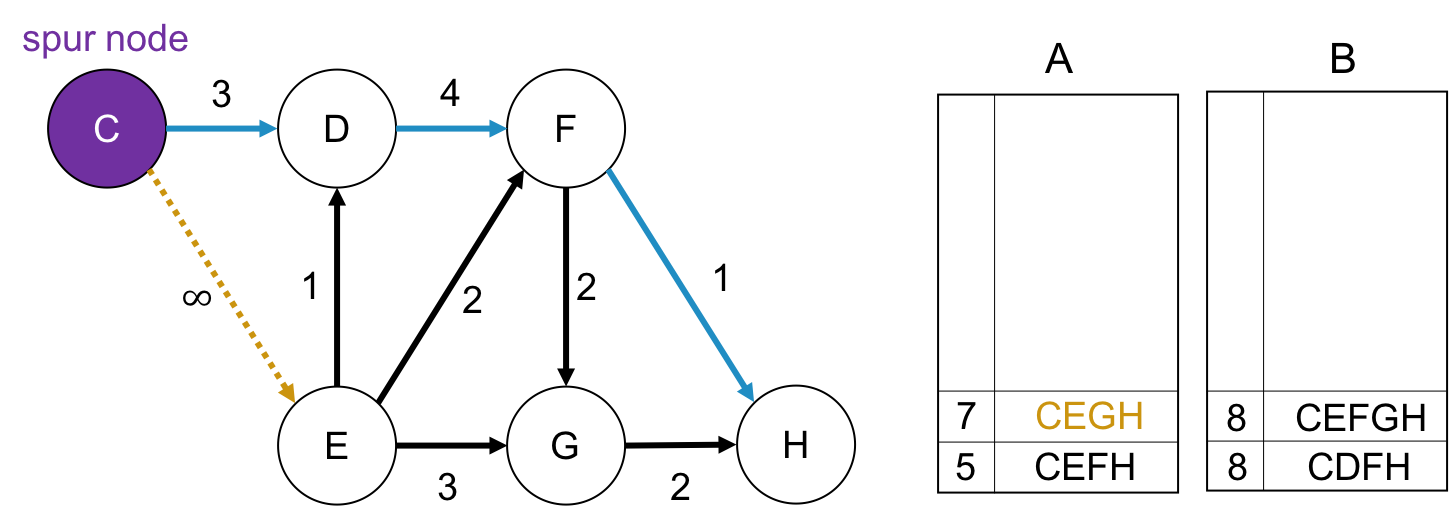
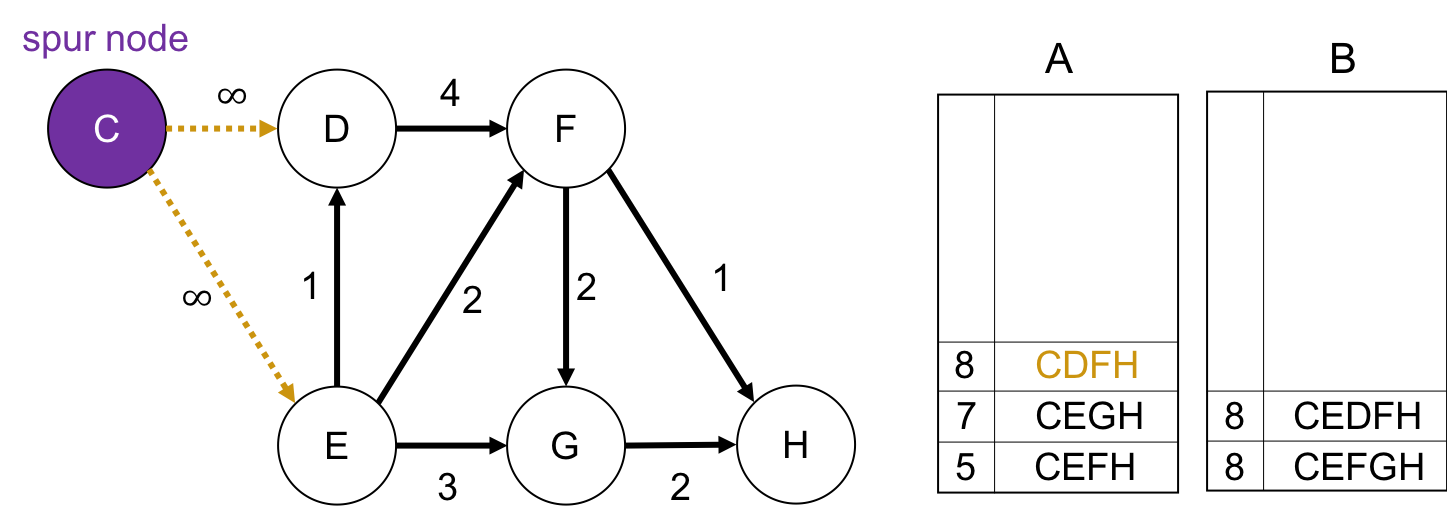
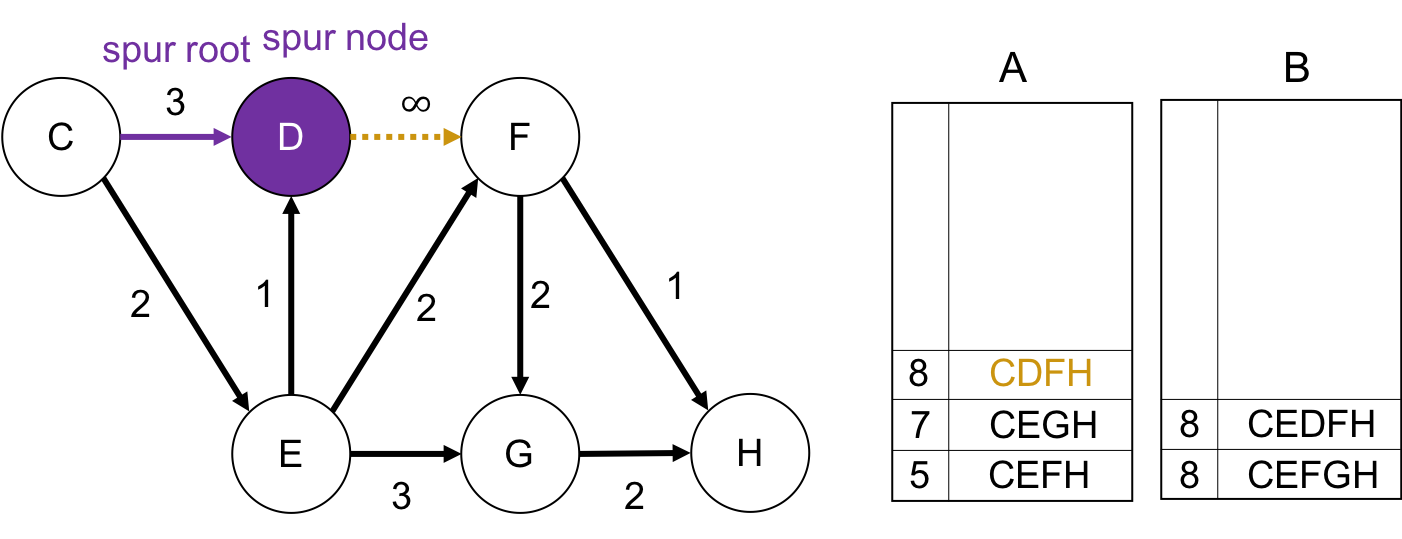
spur node が Cの場合
spur node が Dの場合
sour nodeから終点までのパスが存在しないので, 何もしません.
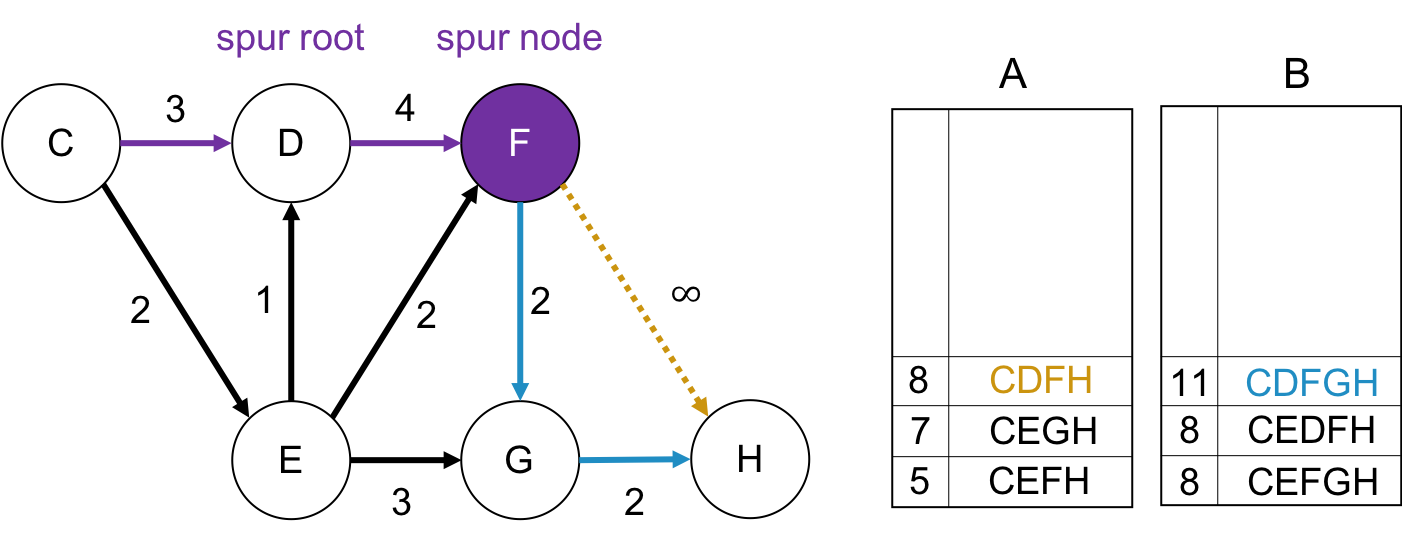
spur node が Fの場合
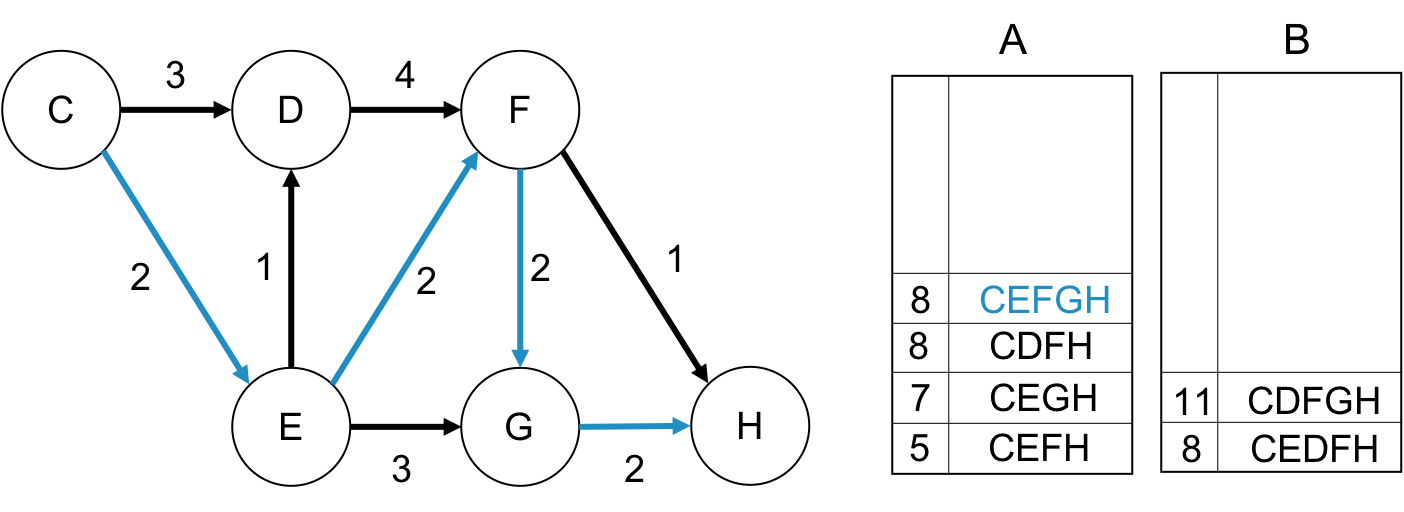
第4最短路の取り出し
計算量
グラフの枝の重みが全て非負の場合, 最短路計算に計算量$O(N^2)$のダイクストラを使えるので全体の計算量は $O(KN^3)$ となります. ただし, Fibonacci heapを使えば計算量が$O(M+N\log N)$ ($M$は枝の本数)になるため, こちらを用いれば全体の計算量は$O(KN(M+N\log N))$です.
グラフの枝に負の重みを持つものが含まれる場合は, 最短路計算に計算量$O(NE)$の Bellman-Ford法を用いるので, 全体の計算量は$O(KN^2E)$です.
参考文献
[1] Yen, Jin Y. "Finding the k shortest loopless paths in a network." management Science 17.11 (1971): 712-716.