最短経路探索とは
各ノード間を移動するのにかかるコストを考慮して、最短であるノードまでに移動することができる経路を探索することです。
グラフ理論における最短経路問題(さいたんけいろもんだい、英: shortest path problem)とは、重み付きグラフの与えられた2つのノード間を結ぶ経路の中で、重みが最小の経路を求める最適化問題である。
(Wikipediaより)https://ja.wikipedia.org/wiki/%E6%9C%80%E7%9F%AD%E7%B5%8C%E8%B7%AF%E5%95%8F%E9%A1%8C
今回は、以下の条件で最短経路探索を試してみたいと思います。
・A地点からC地点まで移動したい
・A地点→C地点まで移動するのに徒歩で20分かかる
・A地点→B地点までバスで5分で到着する
・B地点→C地点まで移動するのに徒歩で6分かかる
実際にやってみる
テストデータの作成
CREATE(A:Node{name:"A"}), (B:Node{name:"B"}),(C:Node{name:"C"}),
(A)-[:CONNECT{cost:20}]->(C), (A)-[:CONNECT{cost:5}]->(B), (B)-[:CONNECT{cost:6}]->(C)
作成されたテストデータは以下のようになります。
MATCH(A:Node{name:"A"}), (B:Node{name:"B"}), (C:Node{name:"C"})
RETURN A, B, C

2つのノード間の最短経路を取得する
MATCH(from:Node{name:"A"}), (to:Node{name:"C"}), p=shortestpath((from)-[:CONNECT]->(to))
RETURN p;

shortestPathは、2つのノード間の最短距離を表示し、プロパティを考慮しません。
プロパティを考慮した最短経路を取得する
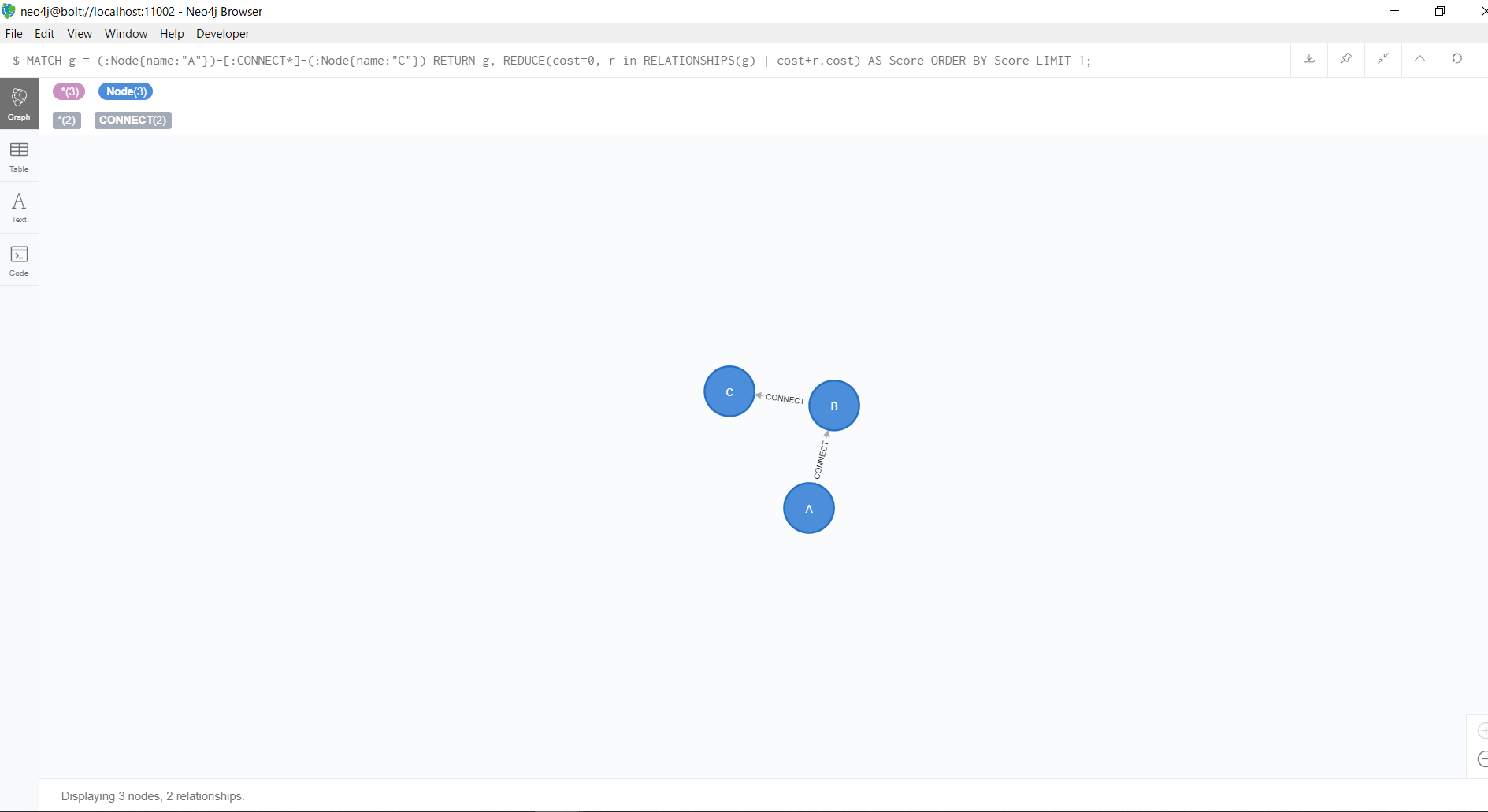
MATCH g = (:Node{name:"A"})-[:CONNECT*]-(:Node{name:"C"})
RETURN g, REDUCE(cost=0, r in RELATIONSHIPS(g) | cost+r.cost) AS Score
ORDER BY Score
LIMIT 1;
MATCHでA地点からC地点に向かう全ての経路を取得し、変数gに代入しています。
REDUCE関数でそれぞれの経路ごとのcost値を加算しています。
加算した値を昇順に並べ替え、一番値の小さい経路を返しています。
※追記
上記のクエリには、全てのパスを比較して結果を返すという欠陥があることが判明いたしました。今回のテストデータでは、総パス数が少ないために結果が返ってきましたが、パスの数が一定以上多くなると、メモリ不足によりクエリを投げたのに結果が返ってこなくなってしまいます。
パス数を増やしたデータを用いて、上記のクエリを実行してみます。
LOAD CSV WITH HEADERS FROM "https://gist.githubusercontent.com/lassewesth/634281cced11147432cf232a2c36e080/raw/1ed1f4fe4ca4c8092bbc8557addd1e5d87316833/eroads.csv" AS row
RETURN row
LIMIT 10
CREATE CONSTRAINT ON (p:Place)
ASSERT p.name IS UNIQUE
USING PERIODIC COMMIT 1000
LOAD CSV WITH HEADERS FROM "https://gist.githubusercontent.com/lassewesth/634281cced11147432cf232a2c36e080/raw/1ed1f4fe4ca4c8092bbc8557addd1e5d87316833/eroads.csv"
AS row
MERGE (origin:Place {name: row.origin_reference_place})
SET origin.countryCode = row.origin_country_code
MERGE (destination:Place {name: row.destination_reference_place})
SET destination.countryCode = row.destination_country_code
MERGE (origin)-[eroad:EROAD {road_number: row.road_number}]->(destination)
SET eroad.distance = toInteger(row.distance), eroad.watercrossing = row.watercrossing
以下のコードを実行します。
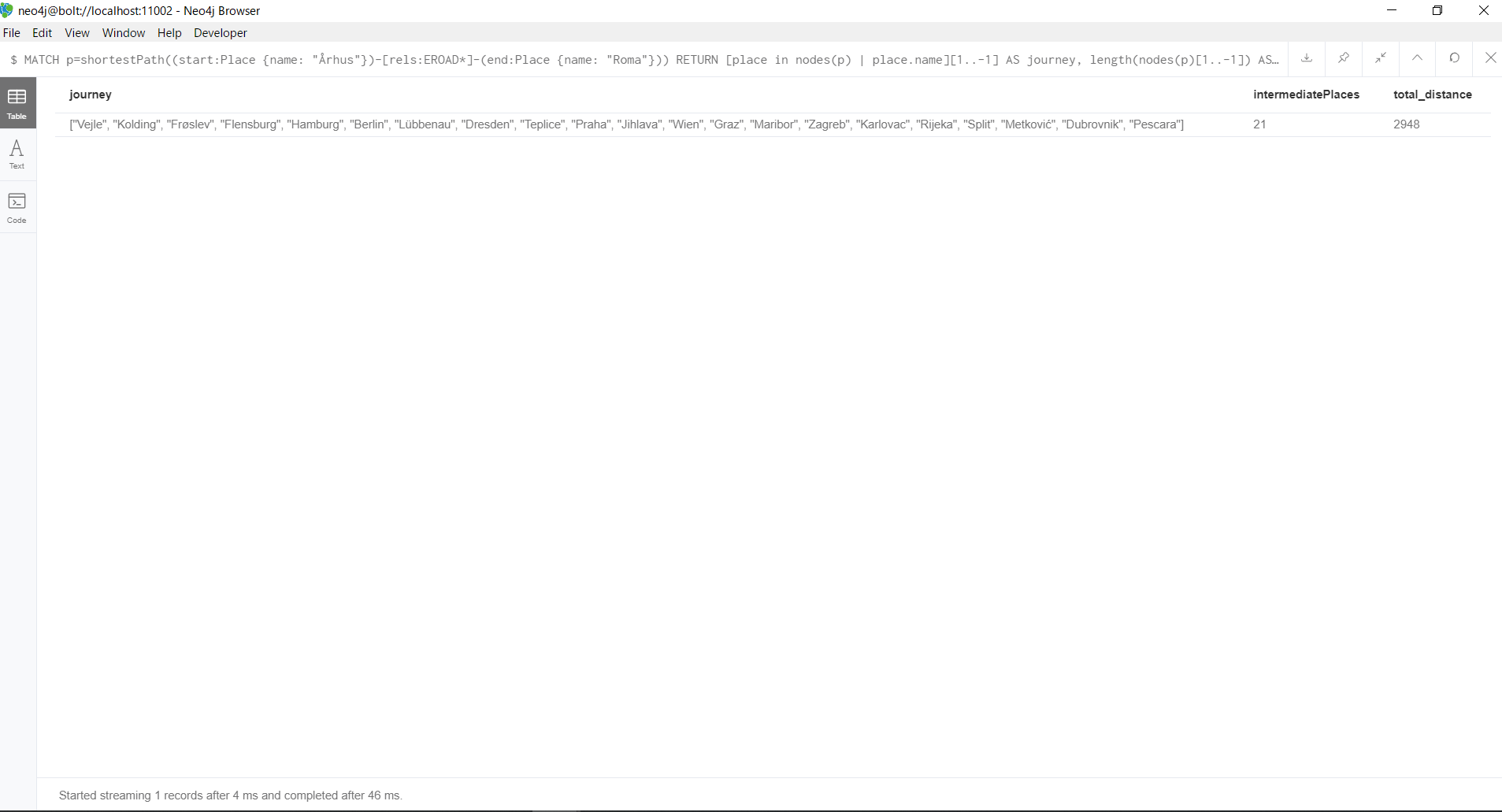
MATCH p=shortestPath((start:Place {name: "Århus"})-[rels:EROAD*]-(end:Place {name: "Roma"}))
RETURN [place in nodes(p) | place.name][1..-1] AS journey,
length(nodes(p)[1..-1]) AS intermediatePlaces,
reduce(s = 0, r in rels | s + r.distance) AS total_distance
結果はこのようになります。shortestPath()関数を使用すると、ÅrhusからRomaまでの最短経路(最小のホップ数を持つ経路)が返ってきます。(※あくまで最小のホップ数をもつ経路です。)
次に、以下のコードを実行します。
MATCH p=((start:Place {name: "Århus"})-[rels:EROAD*]-(end:Place {name: "Roma"}))
RETURN [place in nodes(p) | place.name][1..-1] AS journey,
length(nodes(p)[1..-1]) AS intermediatePlaces,
reduce(s = 0, r in rels | s + r.distance) AS total_distance
以下のように、クエリを投げてからは待てど暮らせど応答がなくなってしまいます。
これは、ÅrhusからRomaまでの全ての経路を探索する必要があるため、計算に多くの時間を要しているためです。いわゆる「組み合わせ爆発」が起こってしまっています。
https://ja.wikipedia.org/wiki/%E7%B5%84%E5%90%88%E3%81%9B%E7%88%86%E7%99%BA
ÅrhusからRomaまでの最短距離をもつ経路(プロパティ値を考慮した最短経路)は、algo.shortestPath.streamを実行することで得られます。
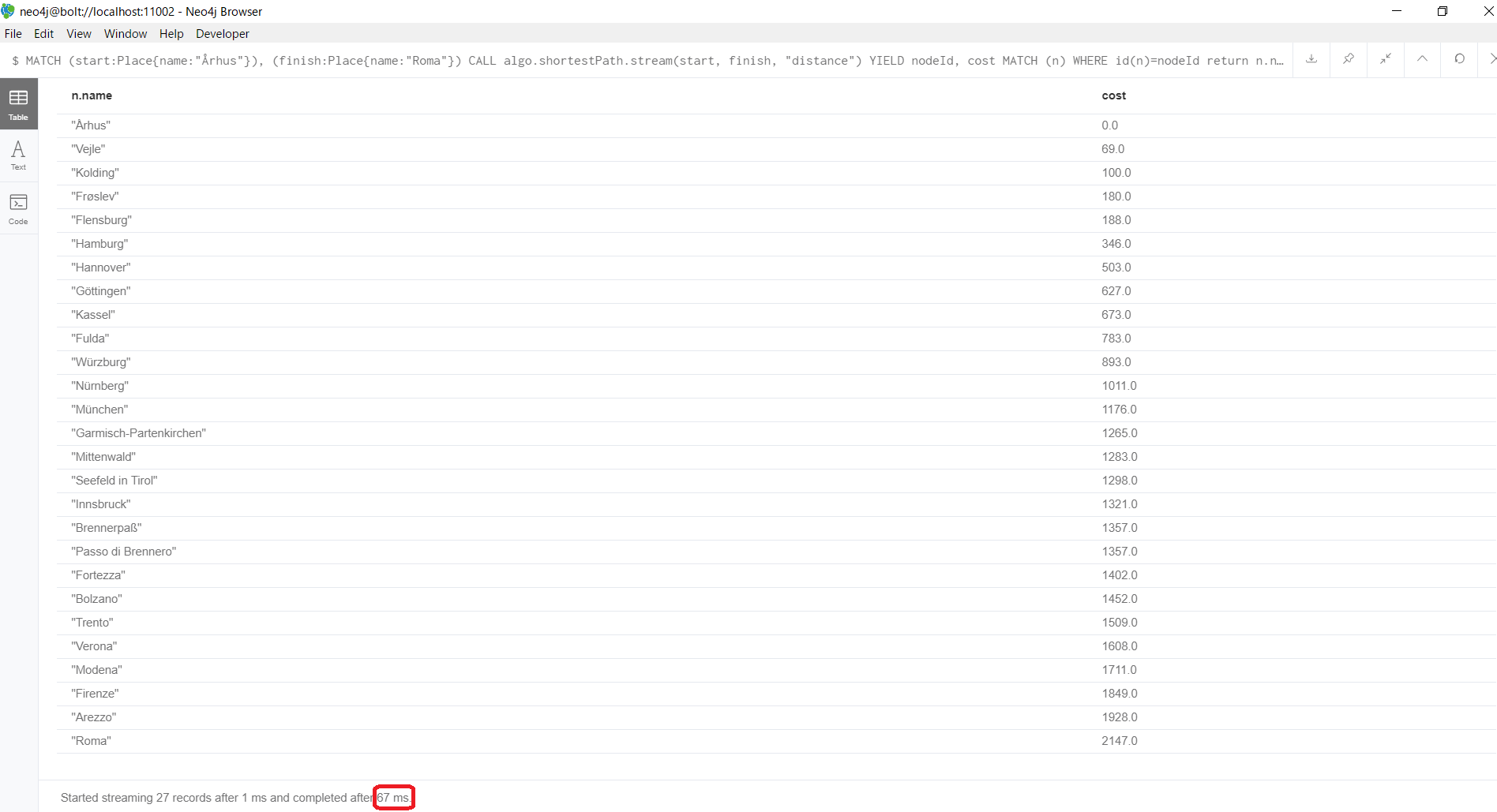
MATCH (start:Place{name:"Århus"}), (finish:Place{name:"Roma"})
CALL algo.shortestPath.stream(start, finish, "distance")
YIELD nodeId, cost
MATCH (n) WHERE id(n)=nodeId
return n.name, cost
クエリを投げてからキャッシュされるまで、たったの67msでした!
REDUCE関数
ここで使用したREDUCE()関数についてまとめます。
REDUCE(accumulator = initial, variable IN list | expression)
accumulaor
初期値をもつ変数です。
initial
ここで初期値を設定します。
variable
リストから一件ずつ取り出した値をもちます。どのプロパティの変数を使用するかはここで決めます。
list
リストをもちます。
RELATIONSHIPS関数
RELATIONSHIPS関数は、指定したパスのリレーションをリストで返します。
参考
https://neo4j.com/docs/cypher-manual/current/functions/list/#functions-reduce
https://neo4j.com/docs/graph-algorithms/current/algorithms/shortest-path/
最後に
こんな書き方もあるよ、などございましたら、編集リクエストに投稿していただけると幸いです。