AAAIに採択された論文です。Data Augmentationの1手法であるMixupを発展させた論文になります。
概要を2行で
- 中間層の出力をMixupするManifold mixupの提案
- 従来の入力をMixupする手法よりも高い精度を得た。
Mixupってなんだっけ?
MixupはData Augmentationの一手法であり,$X_i$をサンプル$i$の説明変数,$y_i$をそのラベルと置くと,以下の式で表されます。
$X = \lambda X_1 + (1 - \lambda) X_2 $
$ y = \lambda y_1 + (1 - \lambda) y_2 $
式から分かるように,説明変数とラベルを一定の係数$\lambda \in [0, 1]$で足し合わせる手法です。ちなみに$\lambda$はベータ分布$Be(\alpha, \alpha)$からサンプリングされます。
元論文では画像の矩形のマスクをランダムに行うData AugumentationであるRandom Eracingと比較して良い精度を出しているようです。
Random Eracingに関してはこちらが詳しいです。
詳細な理論は省きますが,よく「クラス間の中間のデータを作ることで汎化性能を高くする境界平面を上手く学習する」みたいな文脈で説明されることが多いです。
Manifold Mixupとは?
本手法は一言で言うと,入力データではなく,__ある中間層(入力層含む)の出力をMixupする__手法となります。
手順は以下の通りです。
- ランダムに層$k$を選ぶ(入力層含む)
- ランダムに選んだデータの組$(x, y), (x', y')$を上記で選んだ層$k$まで通常通りに計算する。(random minibatchと言ってるので,組は複数でも良さそう)
- 層$k$における出力をそれぞれ$g_k(x), g_k(x')$とおくと,左記出力に対して以下の式でMixupを適用する。$(\tilde{g_k}, \tilde{y}) := (Mix_\lambda (g_k(x), g_k(x')), Mix_\lambda (y, y'))$
- Mixupした中間層の出力をそのまま最終層まで伝播させてLossを計算する
割と単純ですね。すみませんが,理論は省きます。
効果を可視化
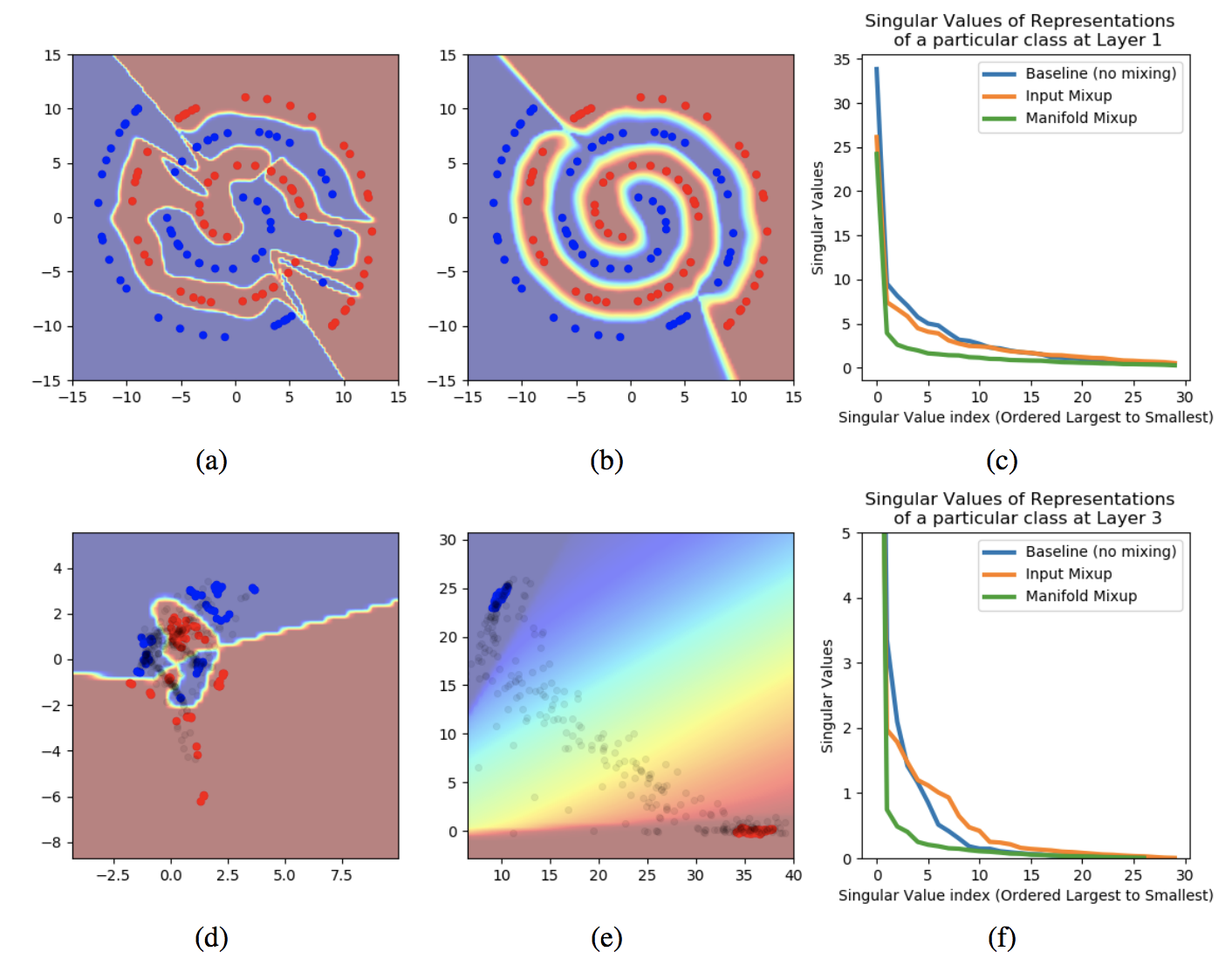
筆者によると,Manifold Mixupは決定境界を滑らかにする効果がある模様。特に,入力の決定境界だけではなく,中間表現の決定境界を滑らかにすることができるようです。この論文では渦の2クラス分類問題でそれを示しています。(論文からの引用です。)
上記(a), (b)はバニラな学習と提案手法の決定境界を表した図になります。バニラな場合は渦の隙間に別クラスの領域が入ってしまっていますが,提案手法はきちんと渦を描けています。加えて(d), (e)は中間層の決定境界です。これはかなりわかりやすいですね。バニラだと平面が複雑ですが,提案手法だと青と赤がはっきり分かれてます。
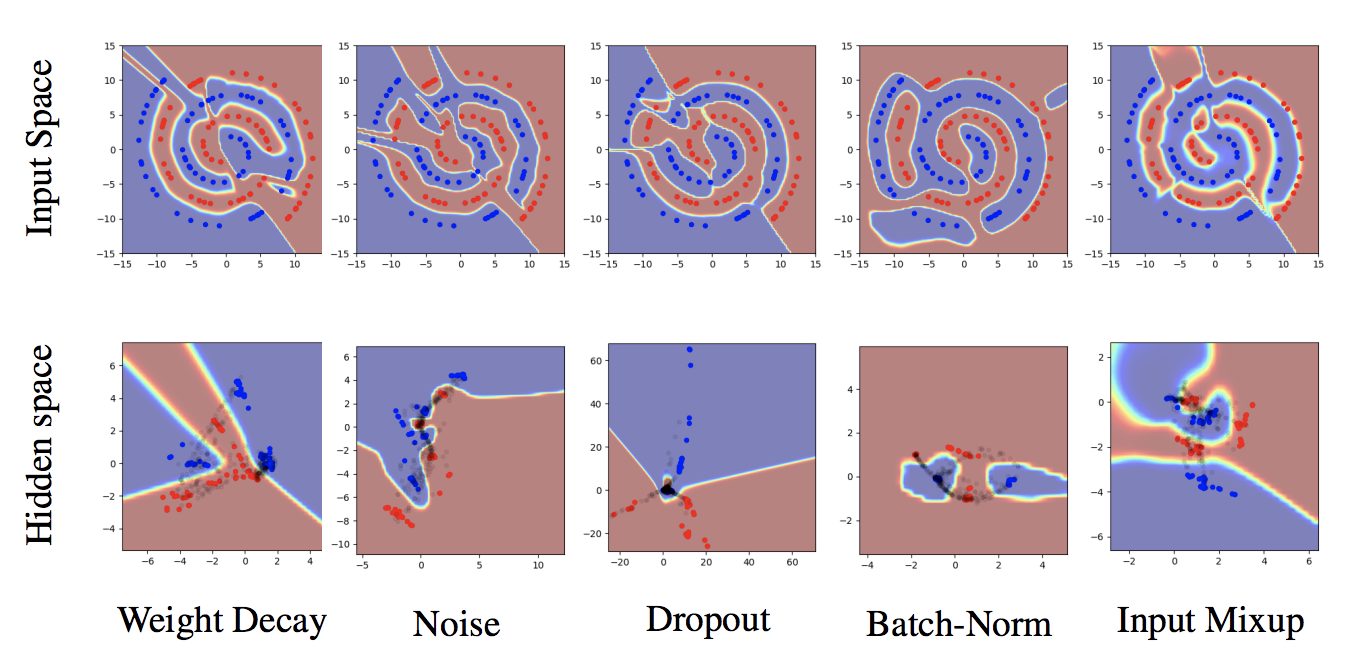
下の図では他の正則化手法と比較してます。普通のMixupでも中間層はやっぱり上手く行ってないですね。あとBatchNormすごい。
(決定境界ってどうやって描画してるんだろう...)
実験
Cifar10, Cifar100での精度の比較を行った結果が以下です。(論文からの抜粋です。)
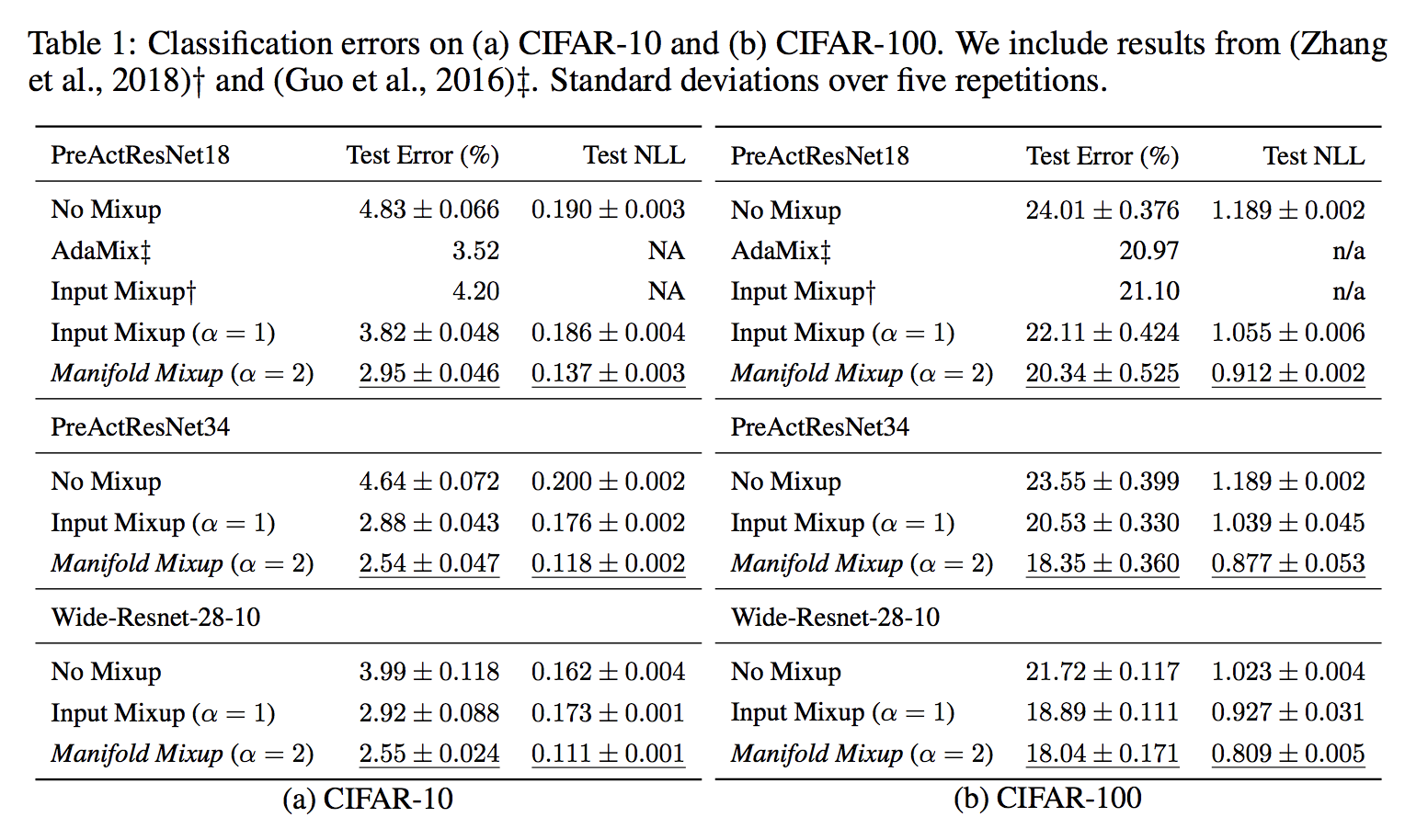
NLLはNegative Log Likelihoodです。ResNetだけでいいのかなという感じはしますが,他の手法よりもTest Errorが低かったことがわかります。(Adamixは論文探しても出てきませんでしたが,提案手法に似た手法で,データのオーバーラップを防ぐために分布を考慮してデータをミックスする手法のようです。)
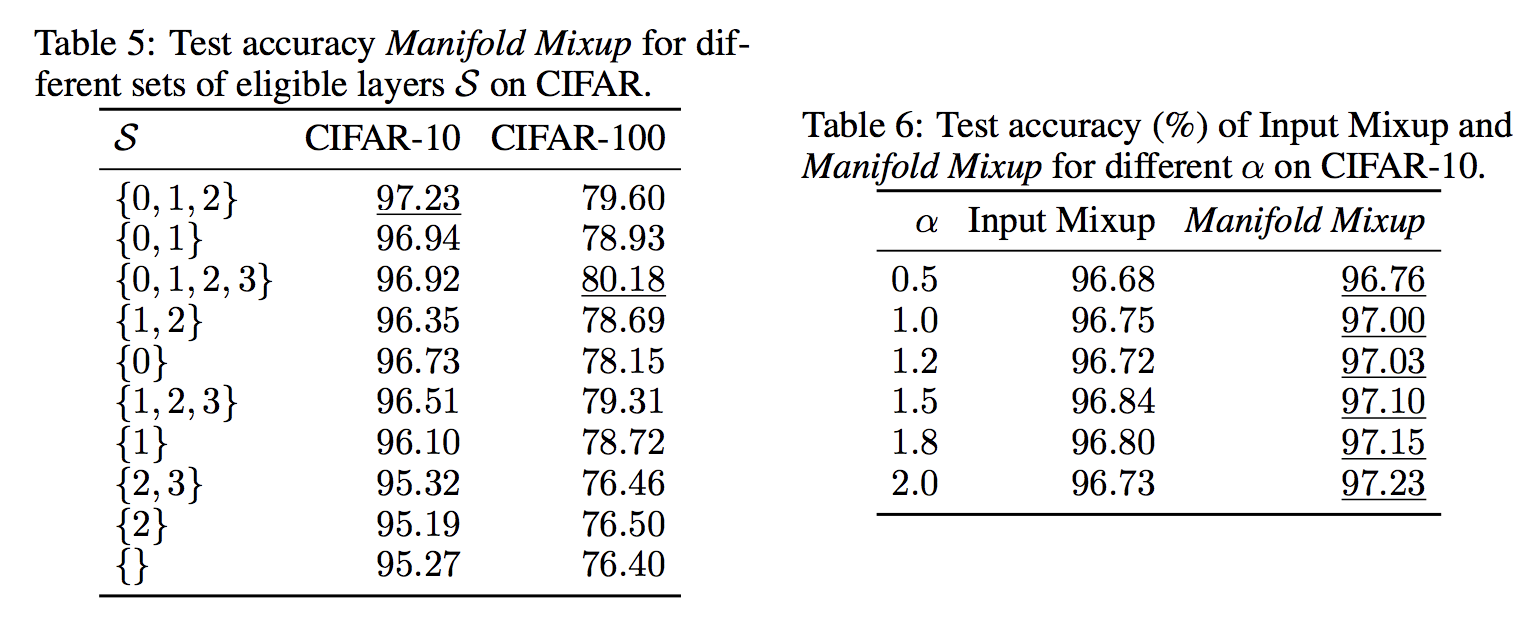
また,筆者は上記の表でMixupを行う中間層の集合の要素数や$\lambda$を生成する$\alpha$を変動させた表を提示して,ハイパーパラメータへの頑健性を主張しています。プレーン(空集合)より全て精度が上がっているのがいい感じですね。
筆者の実装
pytorchで実装されているので参考までに。
https://github.com/vikasverma1077/manifold_mixup