【競技プログラミング】巨大ナップサック問題をやってみた【組合せ最適化】

1.初めに

・アルゴリズムを学ぶために、競技プログラミングを始めました。
・AOJのコースをやっていくので、その備忘録を残します。

・前回は個数制限付きナップサック問題を解いたので、今回は「巨大ナップサック問題」を解いていきます。

2.巨大ナップサック問題

2.1問題

価値が $v_i$ 重さが $w_i$ であるような $N$ 個の品物と、容量が $W$ のナップザックがあります。次の条件を満たすように、品物を選んでナップザックに入れます：

・選んだ品物の価値の合計をできるだけ高くする。
・選んだ品物の重さの総和は $W$ を超えない。

価値の合計の最大値を求めてください。

入力

１行目に２つの整数　$N$、$W$　が空白区切りで１行に与えられます。 続く $N$ 行で $i$ 番目の品物の価値 $v_i$ と重さ $w_i$ が空白区切りで与えられます。

出力

価値の合計の最大値を１行に出力してください。

制約

$1 ≤ N ≤ 100$
$1 ≤ v_i ≤ 10^{15}$ ←?!
$1 ≤ w_i ≤ 10^{15}$ ←?!
$1 ≤ W ≤ 10^{15}$ ←?!

2.1.1.0-1ナップサック問題Ⅱとの違い

・0-1ナップサックⅡ問題では、$w_i$(品物の重さ)と$W$(ナップサックの容量)がすごいことになってました。$(1 ≤ w_i ≤ 10^7 , 1 ≤ W ≤ 10^9とか)$

・その時は、dp表の$J$を価値に置き換えて計算量を減らし、解決しました。

・しかし!!!!今回は$v$(価値)の制約もヤバイことになっているので、$j$を価値と考えて解決することができなくなっています。
　　　　　　　　　　　　↓　じゃあどうするか

「半分全列挙」という手法で品物の組み合わせを考え、答えが出るまでの計算量を減らします！！！！！

2.2.半分全列挙

・例) ${4,8,2,5,9,7,2,3}$の$8$個の要素の中から、２０以下となる組み合わせの中で、合計値が最大となる組み合わせを求める。




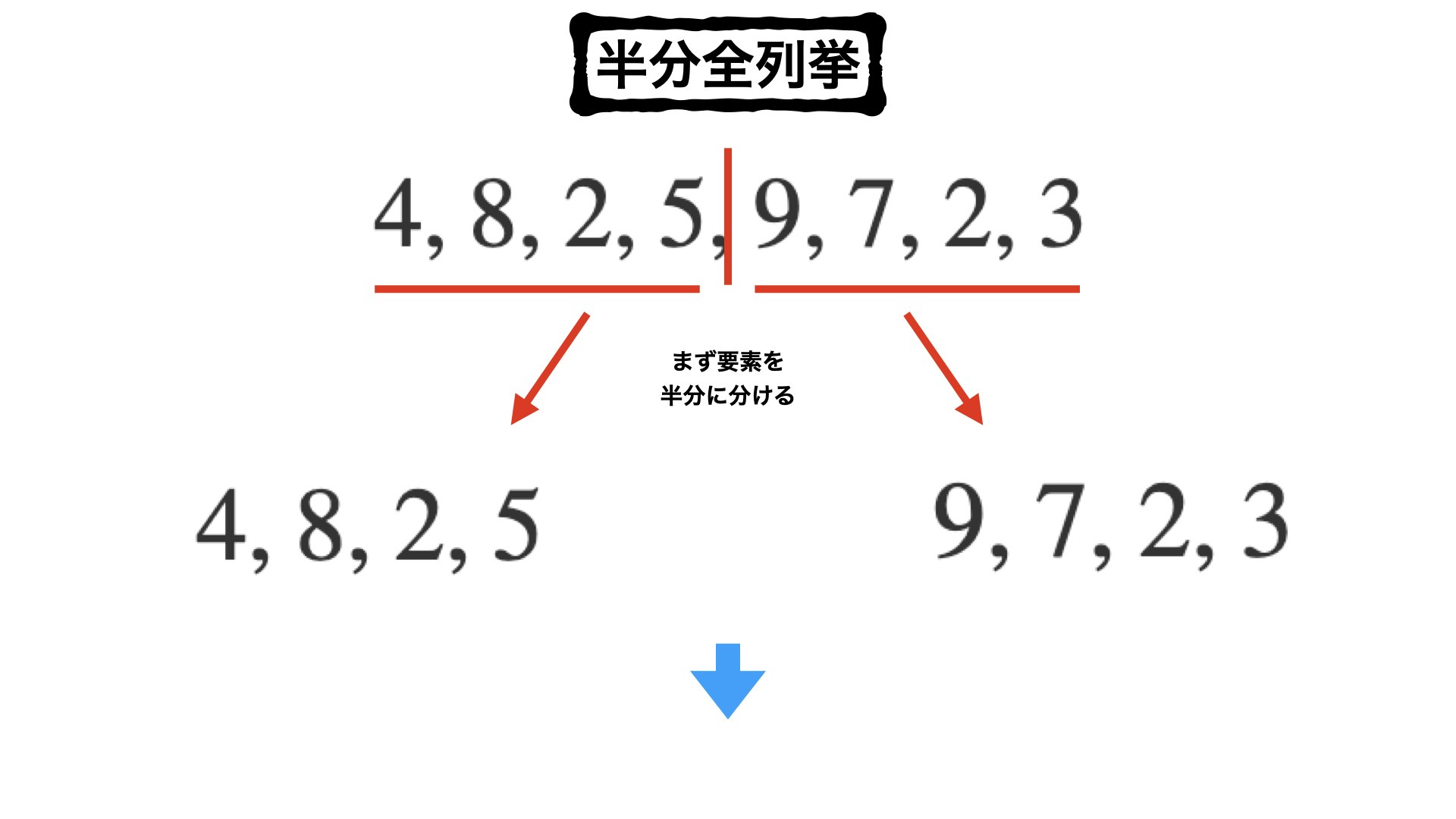
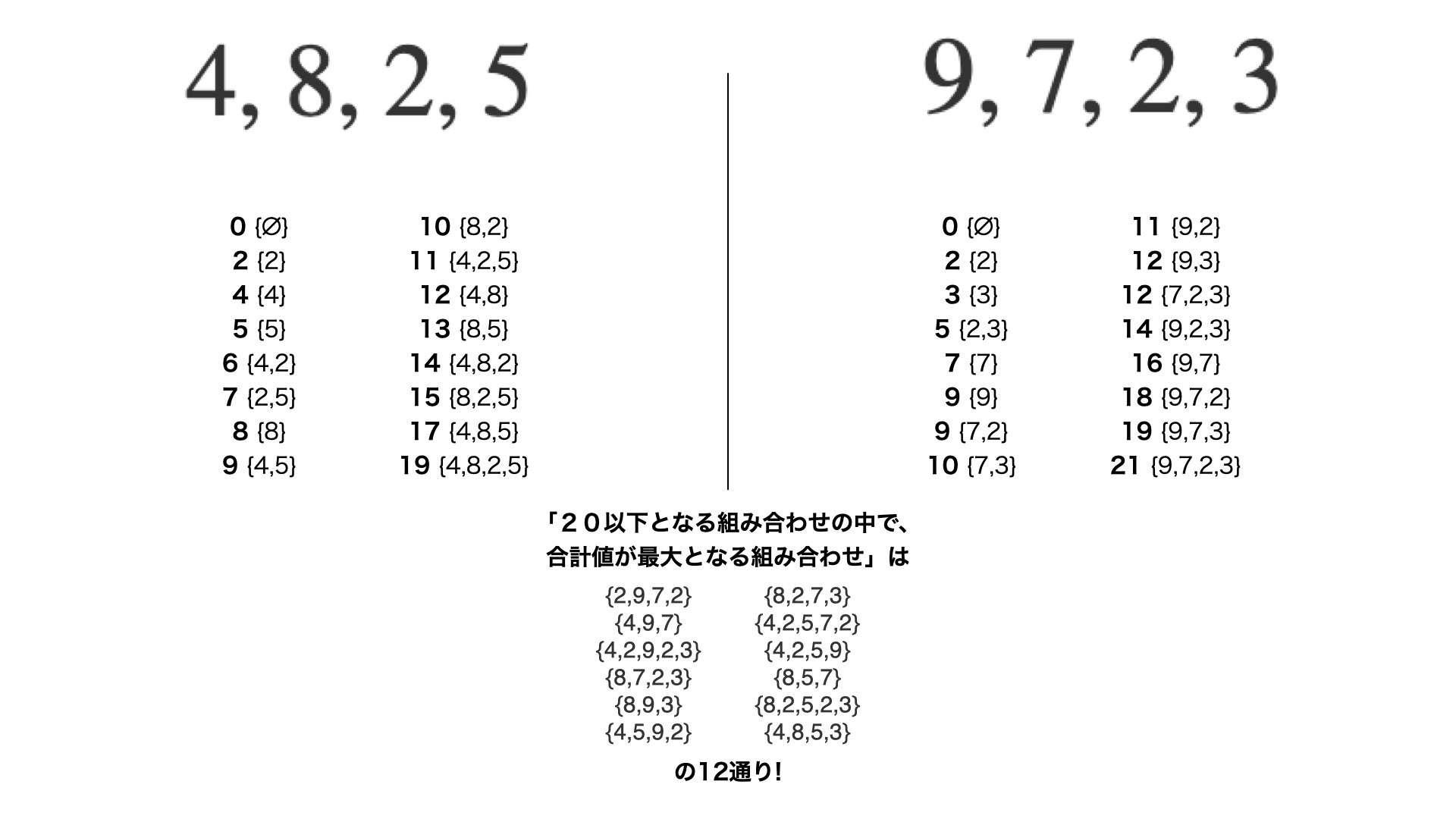
・こんな感じのが、「半分全列挙」の手法です。
・一つずつ組み合わせを考えていくよりも計算量が減ります。

2.2.問題の解き方

・下記の入力例を元に考えてみます。

4 5
5 2
4 2
2 1
8 3

・求めたいのは、「容量W=5を超えないで、価値が最大となるような、商品の組み合わせ」となっています。

・まずは「半分全列挙」の手法通り、4つの品物を半分に分けます。

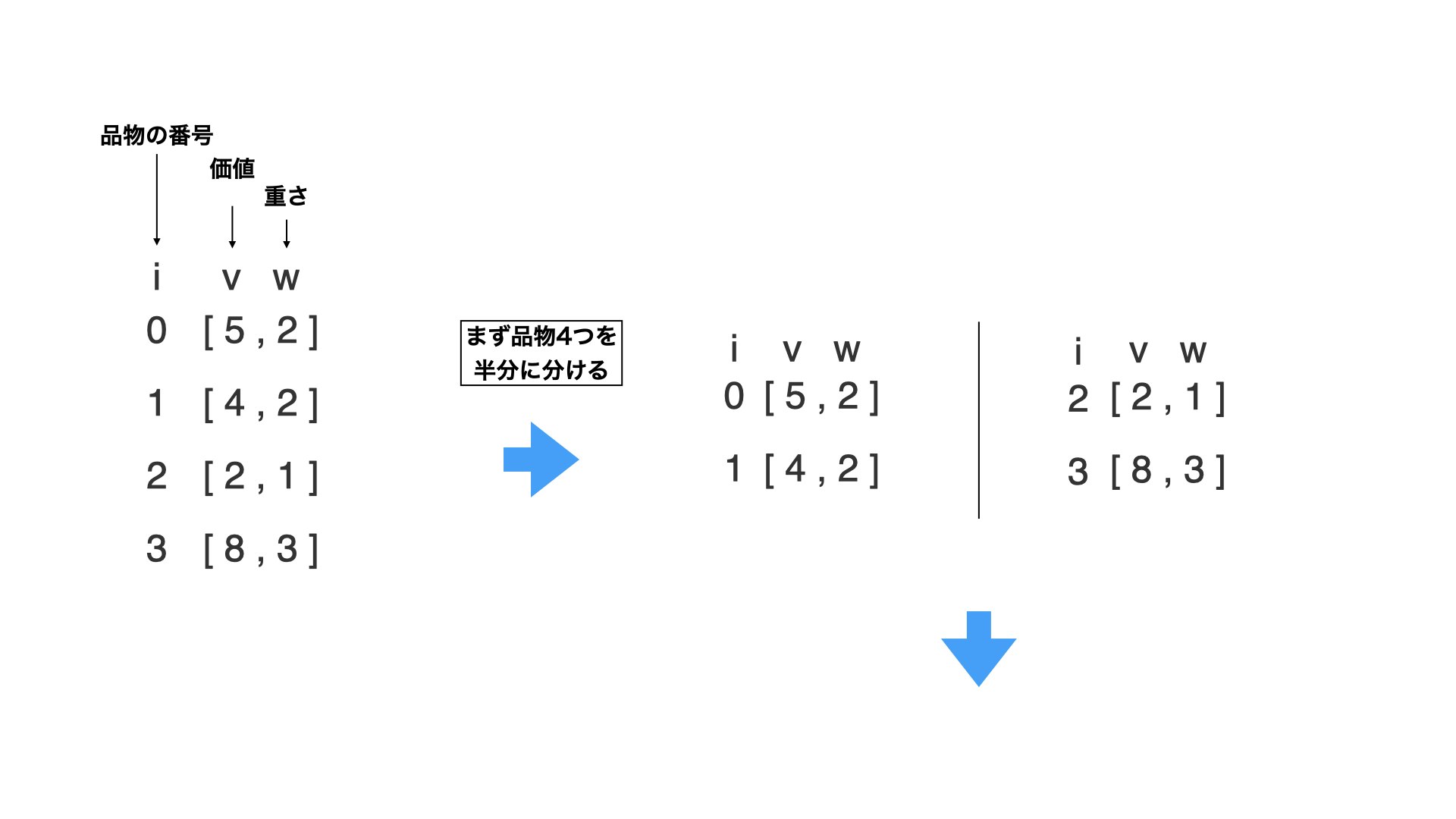
・次に、品物の組み合わせを考えます。(品物を選ばない場合、品物０を選んだ場合、、、全ての品物を選んだ場合、みたいな感じです。)

・そして重さの合計値でソートをかけます。(小さい順に並び替えます。)

・次に、価値の合計値を比較していき、もし価値の合計値が一個前よりも小さかった場合、塗り替えます。(これは逆から回す時に、計算が狂うのを防ぐためです。)

・最後に逆から回して重さの合計と容量を比較し、容量目一杯となる重さの合計の時の価値の合計を出します。

2.3.実装

N,W=map(int,input().split())

# 品物を半分に分ける
n1=N//2
n2=N-n1

# それぞれ[価値,重さ]を入れるリストを作る
# 品物を選ばなかった場合の[価値,重さ]を入れておく
vw1=[[0, 0]]
vw2=[[0, 0]]

# それぞれ、「品物を選ばなかった場合」、「品物を一つ選んだ場合」、・・・、「品物を全部選んだ場合」
# の組み合わせに対応する[価値,重さ]をリスト化していく
for _ in range(n1):
  v,w=map(int,input().split())
  for i in range(len(vw1)):
    p=vw1[i][:]
    p[0]+=v
    p[1]+=w
    vw1.append(p)

for _ in range(n2):
  v,w=map(int,input().split())
  for i in range(len(vw2)):
    p=vw2[i][:]
    p[0]+=v
    p[1]+=w
    vw2.append(p)

# 重さでソートする
vw1.sort(key=lambda vw1: vw1[1])
vw2.sort(key=lambda vw2: vw2[1])

# 前後で価値を比較し、大きい順に塗り替えていく
for i in range(len(vw1)-1):
    if vw1[i][0] > vw1[i+1][0]:
        vw1[i+1][0] = vw1[i][0]

for i in range(len(vw2)-1):
    if vw2[i][0] > vw2[i+1][0]:
        vw2[i+1][0] = vw2[i][0]

# 半分全列挙の手法で条件を満たす最大の価値を見つける
ans=0
i=0
for j in range(len(vw1)-1,-1,-1):
    if vw1[j][1]>W:
        continue
    while i<len(vw2):
      if vw1[j][1]+vw2[i][1]>W:
        break
      i+=1
    ans=max(ans,vw1[j][0]+vw2[i-1][0])
print(ans)