1.初めに
・アルゴリズムを学ぶために、競技プログラミングを始めました。
・AOJのコースをやっていくので、その備忘録を残します。
・前回は最長増加部分列問題を解いたので、今回は「0-1ナップサック問題Ⅱ」を解いていきます。
2.0-1ナップサック問題Ⅱ
2.1問題
価値が $v_i$ 重さが $w_i$ であるような $N$ 個の品物と、容量が $W$ のナップザックがあります。次の条件を満たすように、品物を選んでナップザックに入れます。
・選んだ品物の価値の合計をできるだけ高くする。
・選んだ品物の重さの総和は $W$ を超えない。
価値の合計の最大値を求めてください。
入力
1行目に2つの整数 $N$、$W$ が空白区切りで1行に与えられます。 続く $N$ 行で $i$ 番目の品物の価値 $v_i$ と重さ $w_i$ が空白区切りで与えられます。
出力
価値の合計の最大値を1行に出力してください。
制約
$1 ≤ N ≤ 100$
$1 ≤ v_i ≤ 100$
$1 ≤ w_i ≤ 10,000,000$ ←?!
$1 ≤ W ≤ 1,000,000,000$ ←?!
2.1.1.0-1ナップサック問題との違い
・各品物の重さ$w$とナップサックの容量$W$の制約が桁違いに大きくなっています。
↓ そうすると、、、
・DPテーブルの$j$をナップサックの容量として作ると、計算量がヤバいことになります。
↓ じゃあどうするか
jを価値の大きさとして考えます!!
2.2.DPテーブルを作る
・上で説明したように、DPテーブルの$j$をナップサックの容量として作ると、計算量がヤバいことになるので、以下のようにしてDPテーブルを作成していきます。
i:品物の番号
j:価値の大きさ
として
$$\boldsymbol{dp[i][j]=i番目までの品物を使って、jの価値を出すための最小の重さ}$$
としてdp表を埋めていきます。
・$1 ≤ N ≤ 100$、$1 ≤ v_i ≤ 100$ なので、「$j$の最大値$=$最大計算量$=10,000$」となって、「$1 ≤ W ≤ 1,000,000,000$ 」を$j$にして計算をするよりはマシ、ということですね!!
4 5
4 2
5 2
2 1
8 3
・入力例1が↑なので、これを元にDPテーブルを作っていきます。
・i=1、j=0の時
(最初、全部のdp[i][j]には「inf」が入っていますが、見にくいので省略しています。)
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | 0 | inf | inf | inf | inf | inf | inf | inf | inf | ... |
| 4 | 2 | 1 | 次 | ||||||||
| 5 | 2 | 2 | |||||||||
| 2 | 1 | 3 | |||||||||
| 8 | 3 | 4 |
・$dp[1][0]$ は1番目までの品物を使って価値0を出すための最小の重さはなんだ?
↓
・1番目の品物って[価値=4、重さ=2]だなあ。
↓
・1番目の品物の価値(w)=4って既に予定の価値(j)=0を超えてるから、品物使えないじゃん。
↓
・使える品物がないから、最小の重さ($dp[1][0]$ )は0だ!
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | 0 | 0 | inf | inf | inf | inf | inf | inf | inf | inf | ... |
| 4 | 2 | 1 | 0 | ... | ||||||||
| 5 | 2 | 2 | ||||||||||
| 2 | 1 | 3 | ||||||||||
| 8 | 3 | 4 |
みたいな感じです。
・i=2、j=4の時
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | 0 | inf | inf | inf | inf | inf | inf | inf | inf | inf | ... |
| 4 | 2 | 1 | 0 | inf | inf | inf | inf | inf | inf | inf | inf | ... |
| 5 | 2 | 2 | 0 | inf | inf | inf | 次 | |||||
| 2 | 1 | 3 | ||||||||||
| 8 | 3 | 4 |
・$dp[2][4]$ は2番目までの品物を使って価値4を出すための最小の重さはなんだ?
↓
・2番目までの品物って[価値=4、重さ=2]、[価値=5、重さ=2]の二個だなあ。
↓
・[価値=4、重さ=2]はを使えば価値を4にして、重さを最小にできるなあ。
↓
・[価値=4、重さ=2]を使うから、最小の重さ($dp[2][3]$ )は2だ。
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | 0 | 0 | inf | inf | inf | inf | inf | inf | inf | inf | ... |
| 4 | 2 | 1 | 0 | inf | inf | inf | 2 | inf | inf | inf | inf | ... |
| 5 | 2 | 2 | 0 | inf | inf | inf | 2 | |||||
| 2 | 1 | 3 | ||||||||||
| 8 | 3 | 4 |
みたいな感じです。
(i番目までの品物を使ってjの価値をピッタリ出せないところはinfとなってます。)
・自力で埋めるたいところですが、jは$10,000$まであるので、「...」のところまで埋めるのは流石に無理でした。↓
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | 0 | 0 | inf | inf | inf | inf | inf | inf | inf | inf | ... |
| 4 | 2 | 1 | 0 | inf | inf | inf | 2 | inf | inf | inf | inf | ... |
| 5 | 2 | 2 | 0 | inf | inf | inf | 2 | 2 | inf | inf | inf | ... |
| 2 | 1 | 3 | 0 | inf | 1 | inf | 2 | 2 | 3 | 3 | inf | ... |
| 8 | 3 | 4 | 0 | inf | 1 | inf | 2 | 2 | 3 | 3 | 3 | ... |
・$dp[i][j]$を埋める時にまず最初に考えるのが、「$j$と $v$ の値を比較する」です。
↓
・次の①か②で場合分けをします。
①:「j<v」となる時(i番目の品物の価値(v)がjの値を超えてしまっている時)
・その$i$番目の品物は使えない。(使っただけで、価値がオーバーしてしまうから)
↓
・それまでの価値の最大値($dp[i-1][j]$)をそのまま$dp[i][j]$入れる。
・例)i=4、j=2の時:(4個目までの品物を使って価値が2となるような重さの最小値を決めるとき)↓
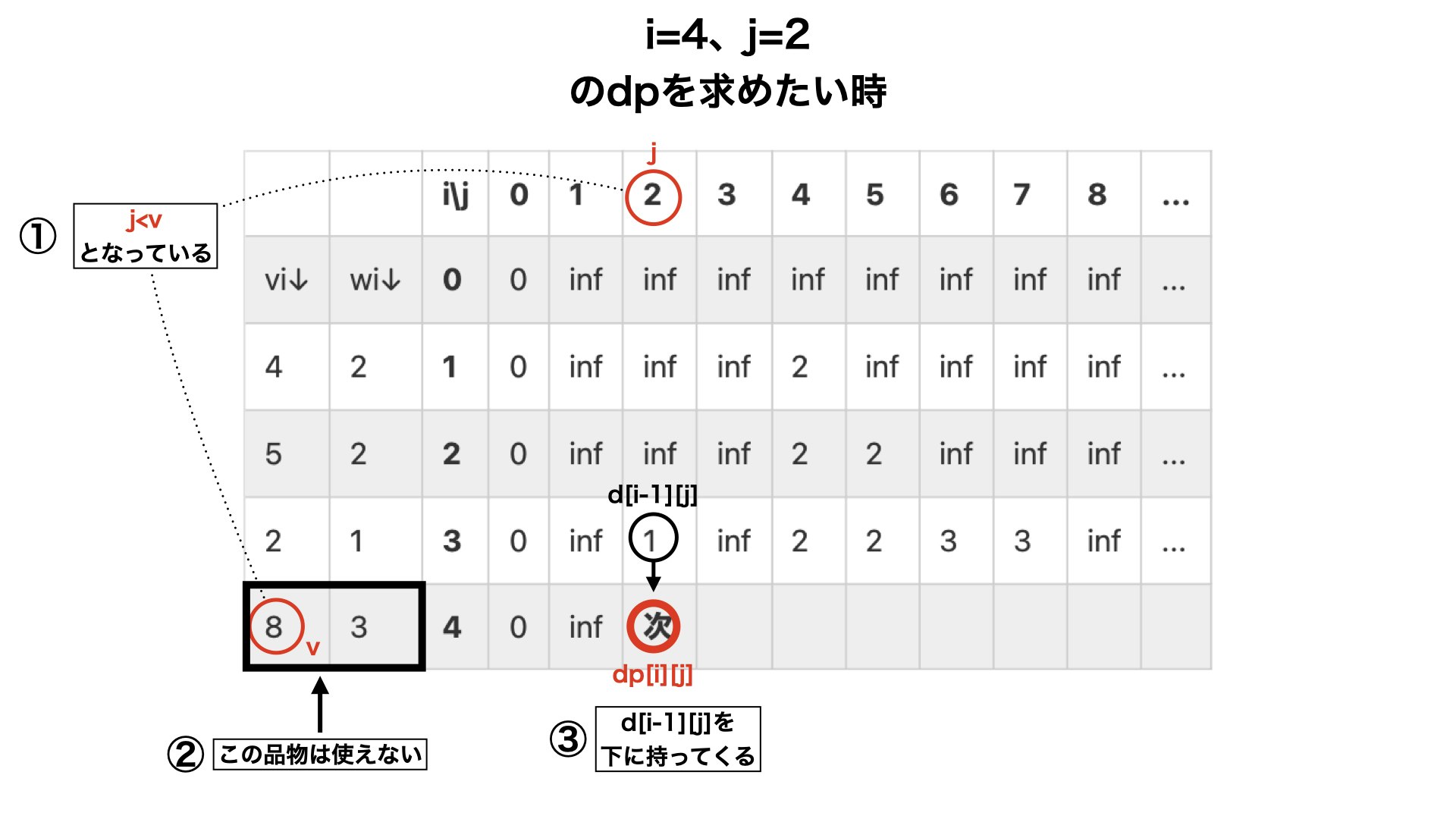
②:「j≥v」となる時(①の逆の場合)
・$dp[i-1][j-v]+w$を計算する。
↓
・$dp[i-1][j-v]+w$と$dp[i-1][j]$を比べて、値の小さい方を$dp[i][j]$に入れる。
・例)i=3,j=6の時:(3個目までの品物を使って価値が6となるような、重さの最小値を決めるとき)
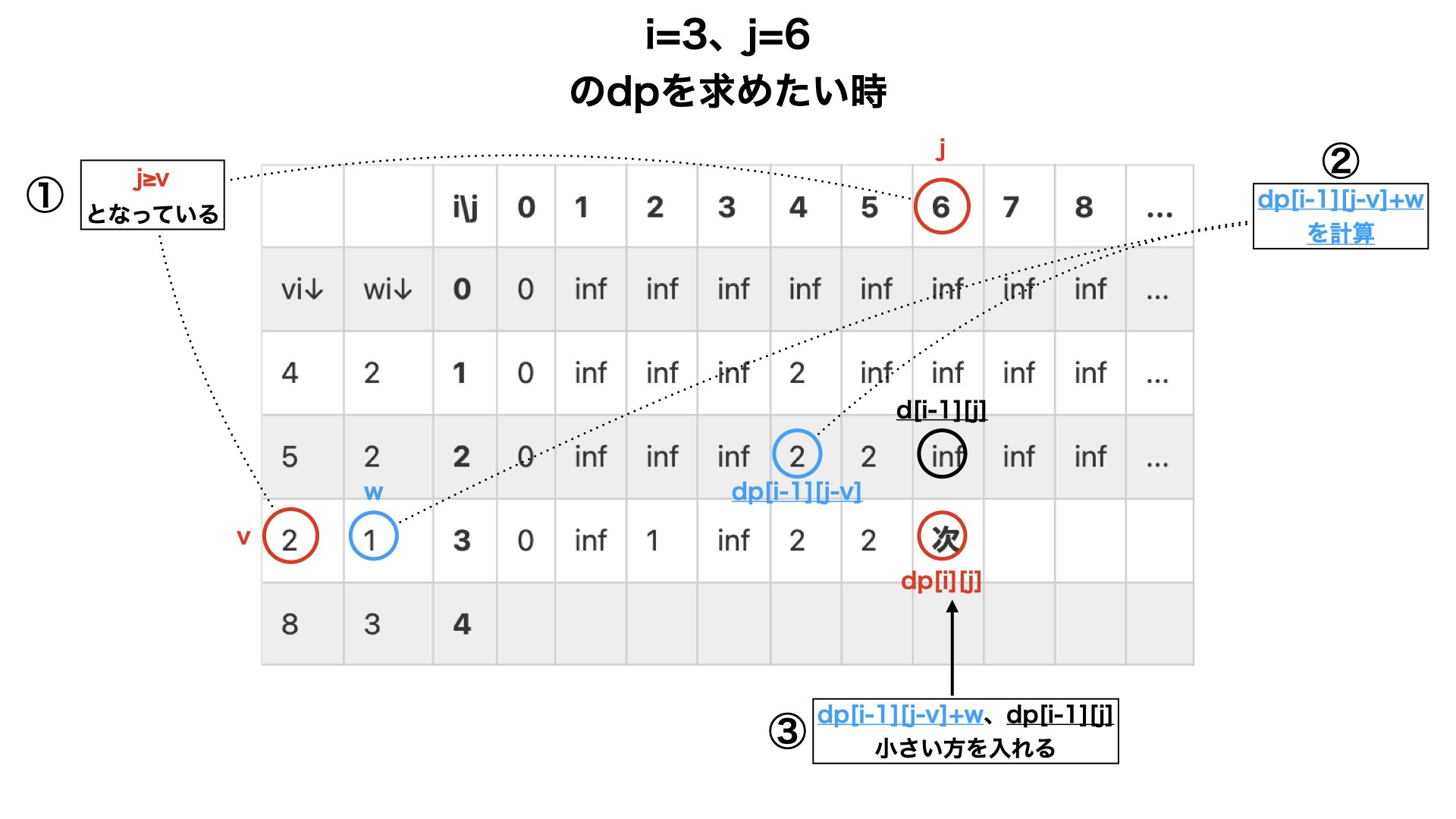
・①、②を式で表すと
dp[i][j] = \left\{
\begin{array}{ll}
dp[i-1][j] & (j<w) \\
max(dp[i-1][j], dp[i-1 ][j-v]+w) & (otherwise)
\end{array}
\right.
となる。
2.3.実装
N,W=map(int,input().split())
# dp表を作る
inf = float("inf")
# 10000+1はjの限界値
dp=[[inf for j in range(10000+1)] for i in range(N+1)]
# 初期値設定
dp[0][0]=0
# dp表を埋めていく
for i in range(1,N+1):
v,w=map(int,input().split())
for j in range(10000+1):
if j<v:
dp[i][j]=dp[i-1][j]
else:
dp[i][j]=min(dp[i-1][j],dp[i-1][j-v]+w)
# 求めたいのは「選んだ品物の重さの合計値(dp[i][j])が容量Wを超えない時の価値(j)の最大値」→条件に当てはまるjを見つける
for j in range(10000,0,-1):
if dp[N][j]<=W:
print(j)
exit()
# 条件を満たす時がない(品物を一つも使えない時)は0を出力
print(0)
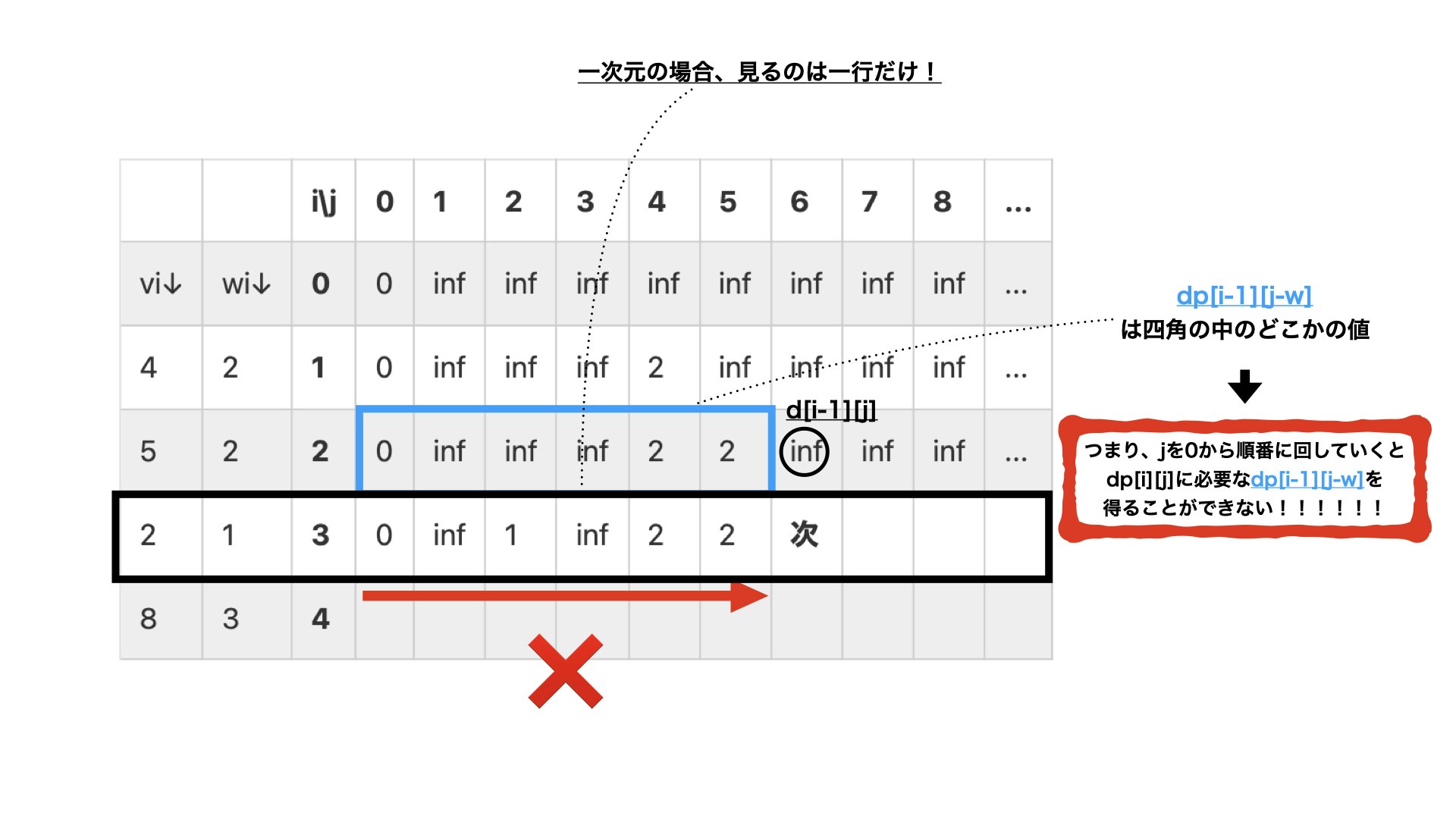
2.4.DP表を一次元にして考える
0-1ナップサック問題Ⅱのdpテーブルも一次元にできます。
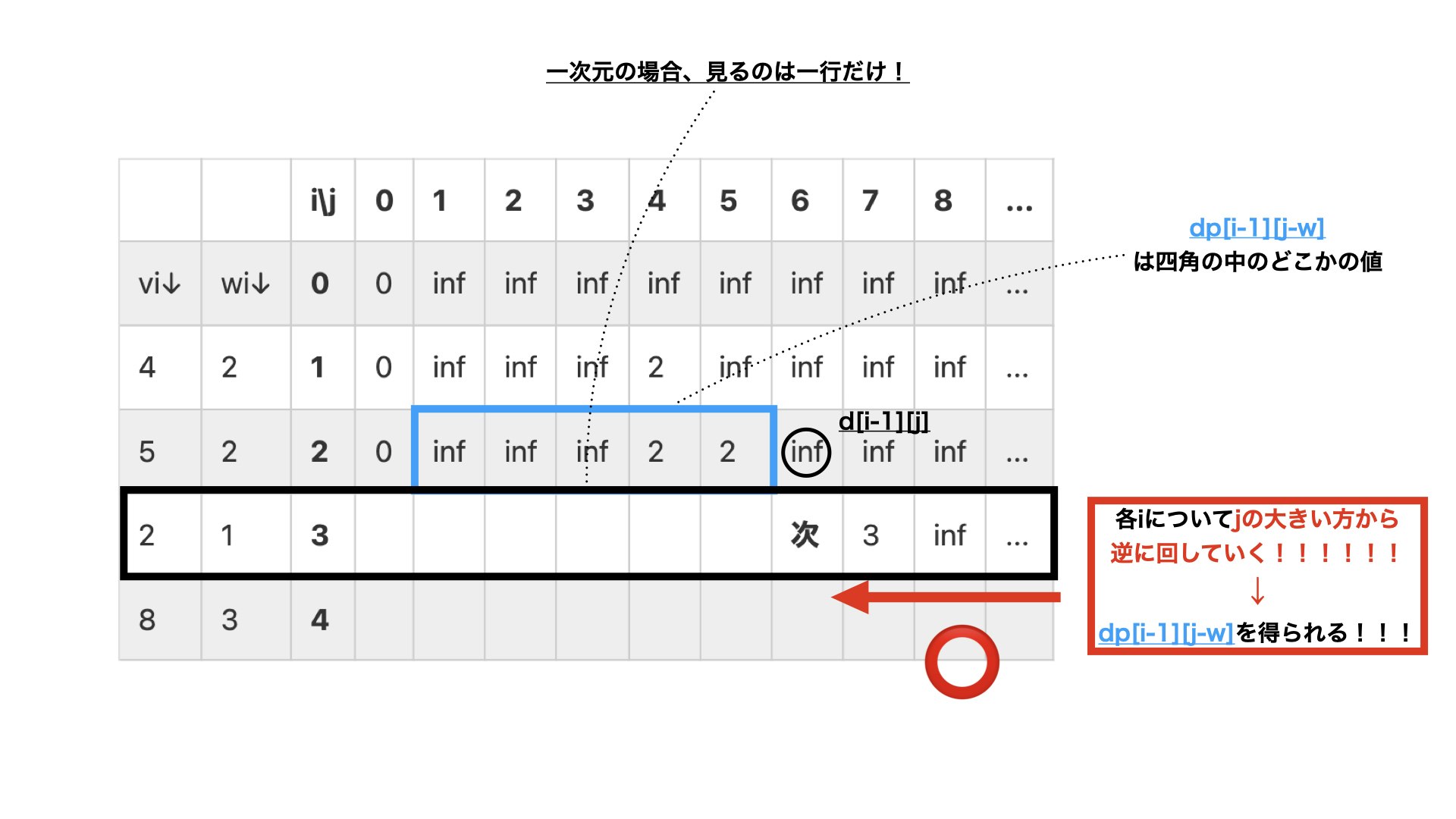
0-1ナップサック問題と同じで、dp[i-1][j-v]+wはi-1行目の値から求めるのでで、jを大きい方から左方向へdp[i][j]を埋めていきます。(二次元配列の時は右方向からでOK)
・例)i=3,j=6の時:(3個目までの品物を使って価値が3となるような、重さの最小値を決めるとき)
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | 0 | 0 | inf | inf | inf | inf | inf | inf | inf | inf | ... |
| 4 | 2 | 1 | 0 | inf | inf | inf | 2 | inf | inf | inf | inf | ... |
| 5 | 2 | 2 | 0 | inf | inf | inf | 2 | 2 | inf | inf | inf | ... |
| 2 | 1 | 3 | 次 | 3 | inf | ... | ||||||
| 8 | 3 | 4 | ... |
・例えば上の表では、3行目をjの大きい方から逆向きに更新して、$dp[3][7]$ まで更新されています。
↓

↓
・次求めたい値(更新する値)が$dp[3][6]$だとします。
↓
・$dp[3][6]=3$と分かりました。
↓
・更新!!
↓
| vi↓ | wi↓ | i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1 | 3 | 0 | inf | inf | inf | 2 | 2 | 3 | 3 | inf | ... |
・みたいな感じで埋めていきます。
・つまり、i番目までの品物を使い、容量jの時の価値の最大値は
$$
dp[j] = max(dp[j], dp[j-v]+w)
$$
と表すことができます。
2.4.1.実装(一次元バージョン)
# 入力値取得
N,W=map(int,input().split())
# DP表(一次元)を作る
inf = float("inf")
dp=[inf]*(10000+1)
dp[0]=0
# dp[i][j]を埋めていく
for i in range(N):
v,w=map(int,input().split())
# 逆から回す
for j in range(10000,v-1,-1):
dp[j]=min(dp[j],dp[j-v]+w)
# 求めたいのは「選んだ品物の重さの合計値(dp[i][j])が容量Wを超えない時の価値(j)の最大値」→条件に当てはまるjを見つける
for j in range(10000,0,-1):
if dp[j]<=W:
print(j)
exit()
# 条件を満たす時がない(品物を一つも使えない時)は0を出力
print(0)