【ラビットチャレンジ（E資格）】深層学習day1

はじめに

本記事はJDLA E資格の認定プログラム「ラビット・チャレンジ」における深層学習day1のレポート記事です。
本記事ではニューラルネットワークの基礎について以下の5つの項目について、要点をまとめています。

• 入力層～中間層
• 活性化関数
• 出力層
• 勾配降下法
• 誤差逆伝搬法

そもそもニューラルネットワークとは？ということで、
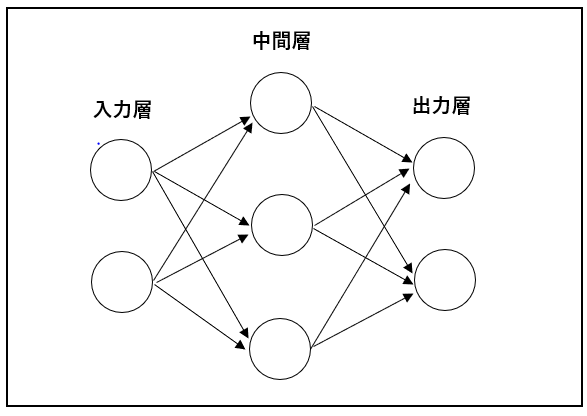
ニューラルネットワークは、人間の脳内にある神経細胞（ニューロン）とそのつながり、つまり神経回路網を人口ニューロンという数式的なモデルで表現したものです。以下の図はニューラルネットワークの一例になります。
入力層、中間層、出力層から構成され、中間層を隠れ層と呼ぶこともあります。そして、この中間層が多数存在する多層構造のニューラルネットワークをディープラーニングといいます。

ニューラルネットワークの活用事例としては、売り上げや株価といった結果の予測、写真や手書き文字などの分類などがあげられます。
それでは、ニューラルネットワークの各機能についてについて要点をまとめていきます。

1. 入力層～中間層

概要

入力層から中間層についてのプロセス図を示します。

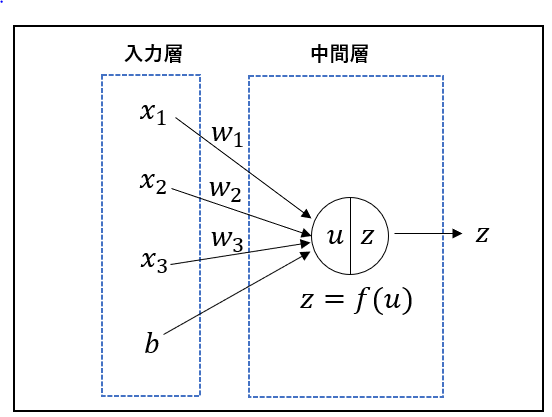
入力層では説明変数が$x_i$が入力されます。中間層では、$x_i$と重み$w_i$が内積されたものに、バイアス$b$が加算されたものが$u$となります。最終的な出力$z$は$u$に活性化関数が乗算されたものになります。
数式で表すと次のようになります。

u=w_ix_i+b

z=f(u)

$x_{i}$：入力(説明変数)
$w_{i}$：各説明変数に対する重み(どれだけ重視するか)
$b$：バイアス
$u$：総入力
$z$：出力
$f$：活性化関数

ニューラルネットワークでは、学習によって$w$と$b$を最適化していきます。

コード実装

入力層～中間層についてnumpyで実装したコードは次のようになります。

入力層～出力層の実装例

# 順伝播（単層・単ユニット）の実装
import numpy as np

# シグモイド関数
def sigmoid(x):
    return 1/(1 + np.exp(-x))

#  出力結果を見やすくする関数
def print_vec(text, vec):
    print("*** " + text + " ***")
    print(vec)

# 重み
W = np.array([[0.1], [0.2]])
print_vec("重み", W)

# バイアス
b = 0.5
print_vec("バイアス", b)

# 入力値
x = np.array([2, 3])
print_vec("入力", x)

# 総入力
u = np.dot(x, W) + b
print_vec("総入力", u)

# 中間層出力
z = sigmoid(u)
print_vec("中間層出力", z)

【実行結果】
*** 重み ***
[[0.1]
[0.2]]
*** バイアス ***
0.5
*** 入力 ***
[2 3]
*** 総入力 ***
[1.3]
*** 中間層出力 ***
[0.78583498]

確認テスト

確認テスト1

• ディープラーニングは何をしようとしているか？
  →　明示的なプログラムの代わりに多数の中間層をもつニューラルネットワークを用いて、入力値から目的とする出力値に変換する数学モデルを構築すること。

• ディープラーニングは、何を最適化することが最終目的か？
  →　重み$[w]$とバイアス$[b]$

確認テスト2

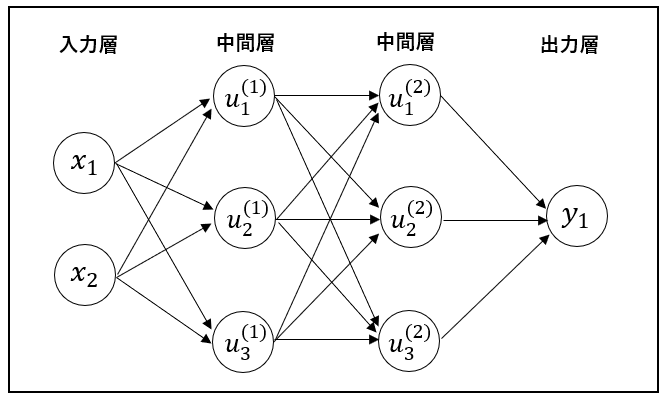
• 次のネットワークを記せ。
  • 入力層：2ノード1層
  • 中間層：3ノード2層
  • 出力層：1ノード1層

解答：

確認テスト3

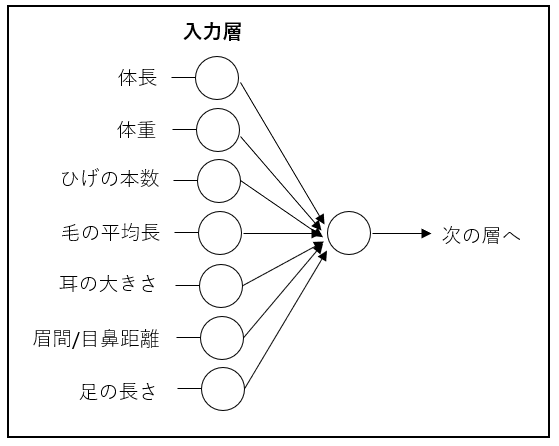
入力層～中間層の図式に動物分類の実例を入れる。

解答：

確認テスト4

次の数式をPythonで書け。

\begin{align}
u&=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+w_{4}x_{4}+b \\
 &=Wx+b
\end{align}

解答：

import numpy as np
u = np.dot(x, W) + b

確認テスト5

「1_1_forward_propagation.ipynb」から中間層の出力を定義しているソースを抜き出せ。

解答：

z2 = functions.relu(u2)

2. 活性化関数

概要

活性化関数は、ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数のことです。
入力の値によって、次の層への信号のON/OFFや強弱を定める働きをします。
それでは、代表的な活性化関数について説明します。

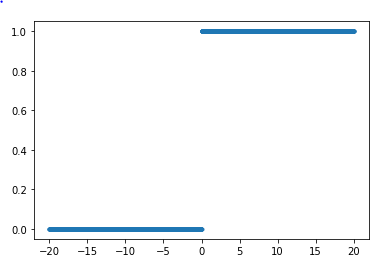
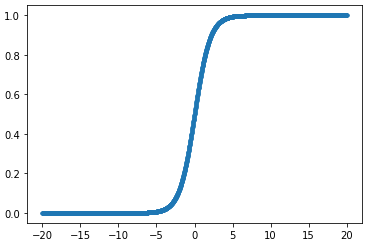
• ステップ関数
  閾値を超えたら発火する関数であり、出力は常に1か0になる。
  ニューラルネットワークの前身であるパーセプトロンでよく利用された関数。
  課題としては、0-1間の間を表現できず、線形分離可能なものしか学習ができない。

f(x)=
\begin{cases}
1 \ \ (x\ge0) \\
0 \ \ (x<0)
\end{cases}

ステップ関数のnumpyでの実装例は次のようになります。

ステップ関数の実装例

import numpy as np
import matplotlib.pyplot as plt

def step(x):
    return np.where( x > 0, 1, 0) 

x = np.array([range(-2000, 2000)])
x = x/100
y = step(x)

plt.scatter(x, y, marker='.')
plt.show()

【実行結果】

• シグモイド関数
  0～1の間を緩やかに変化する関数で、信号の強弱を伝えることができる。
  課題としては、大きな値では出力の変化が微小なため、勾配消失問題を引き起こすことがある。

f(x)=\frac{1}{1+e^{-x}}

シグモイド関数のnumpyでの実装例は次のようになります。

シグモイド関数の実装例

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.array([range(-2000, 2000)])
x = x/100
y = sigmoid(x)

plt.scatter(x, y, marker='.')
plt.show()

【実行結果】

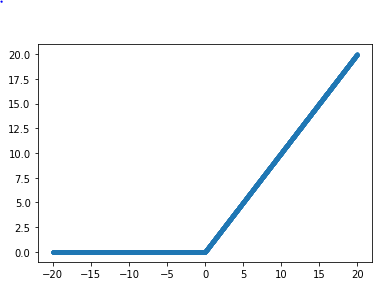
• ReLU関数
  入力が0より大きければそのまま出力し、0より小さければ0とする。
  勾配消失問題の回避やスパース化に貢献することでよい成果をもたらす。

f(x)=
\begin{cases}
x \ \ (x>0) \\
0 \ \ (x\le0)
\end{cases}

ReLU関数のnumpyでの実装例は次のようになります。

ReLU関数の実装例

import numpy as np
import matplotlib.pyplot as plt

def relu(x):
    return np.maximum(0, x)

x = np.array([range(-2000, 2000)])
x = x/100
y = relu(x)

plt.scatter(x, y, marker='.')
plt.show()

【実行結果】

確認テスト

確認テスト1

線形と非線形の違いを簡潔に説明せよ。

解答：

線形な関数は
・加法性：$f(x+y)=f(x)+f(y)$
・斉次性：$f(kx)=kf(x)$
を満たす。

非線形な関数は加法性、斉次性を満たさない。

確認テスト2

「1_1_forward_propagation.ipynb」から活性化関数を使っている箇所を抜き出せ。

解答：

# 1層の総出力
z1 = functions.relu(u1)

# 2層の総出力
z2 = functions.relu(u2)

3. 出力層

概要

出力層と中間層で利用される活性化関数は異なります。
中間層では、閾値の前後で信号の強弱を調整していましたが、出力層では信号の大きさ（比率）はそのままに変換します。
また、分類問題のタスクにおいては、出力層の出力は0～1の範囲に限定し、総和を1となるようにする必要があります。
各タスクにおいて、出力層に用いられる活性化関数、誤差関数についてまとめたものを以下表にまとめました。

	回帰	二値分類	多クラス分類
活性化関数	恒等写像	シグモイド関数	ソフトマックス関数
活性化関数(式)	$f(u)=u$	$f(u)=\frac{1}{1+e^{-u}}$	$f(i,u)=\frac{e^{u_i}}{\sum_{k=1}^K e^{u_k}}$
誤差関数	二乗誤差	交差エントロピー	交差エントロピー

• 2乗誤差

E_n(w)=\frac{1}{2} \sum_{i=1}^{I} (y_{i} - d_{i})^{2}

2乗誤差の実装例

def mean_squared_error(y, d):
  return np.mean(np.square(y-d)) / 2

• 交差エントロピー

E_{n}(w)=-\sum_{i=1}^{I}{d_{i}log\ y_{i}}

交差エントロピーの実装例

def cross_entropy_error(d, y):
  if y.ndim == 1:
    d = d.reshape(1, d.size)
    y = y.reshape(1, y.size)

  if d.size == y.size:
    d = d.argmax(axis=1)

  batch_size = y.shape[0]
  return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7) / batch_size

確認テスト

確認テスト1

• 今回用いた誤差関数に平均2乗誤差を用いたが、ぜ予測と目的変数を引き算だけでなく2乗するのか？
  →引き算を行うだけでは、各ラベルでの誤差で正負両方の値が発生し、全体の誤差を正しくあらわすのに都合が悪い。2乗してそれぞれのラベルでの誤差を正の値になるようにするため。

• 平均2乗誤差はなぜ1/2しているのか？
  →実際にネットワークを学習するときに行う誤差逆伝搬の計算で、誤差関数の微分を用いるが、その際の計算式を簡単にするため。本質的な意味はない。25

確認テスト2

ソフトマックス関数の数式に該当するコードについて1行ずつ処理の説明をせよ。

解答：

# ソフトマックス関数
def softmax(x):
    if x.ndim == 2: # ミニバッチとしてデータを取り扱うときに用いられる
        x = x.T # xを転置してデータ構造を整える
        x = x - np.max(x, axis=0) # オーバーフロー対策、プログラムの動きを安定させる
        y = np.exp(x) / np.sum(np.exp(x), axis=0) # ソフトマックス関数の計算部分
        return y.T # yを転置して出力のデータ構造を整える

    x = x - np.max(x) # オーバーフロー対策、プログラムの動きを安定させる
    return np.exp(x) / np.sum(np.exp(x)) # ソフトマックス関数の計算部分

確認テスト3

交差エントロピーの数式に該当するソースコードを示し、1行ずつ処理の説明をせよ。
（ ソフトマックス関数：　$E_{n}(w)=-\sum_{i=1}^{I}{d_{i}log\ y_{i}}$ ）

解答：

def cross_entropy_error(d, y):
  if y.ndim == 1:    # 1次元の場合。例えば(3,)みたいな形状。
    d = d.reshape(1, d.size)    # (1, 全要素数)のベクトルに変形
    y = y.reshape(1, y.size)    # (1, 全要素数)のベクトルに変形

  # 教師データが one-hot-vector の場合、正解ラベルのインデックスに変換
  if d.size == y.size:
    d = d.argmax(axis=1)  # argmaxで最大値(予測の最も確からしいクラス)のインデックスを取得

  batch_size = y.shape[0] # この場合は行の形状なので1
  return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7) / batch_size
  # 「/ batch_size」までが上記の式に該当(左記の部分は使い勝手を良くするためのもの)
  # np.arangeでバッチサイズ分取り出して対数関数に与えている。
  # 「1e-7」は対数関数の結果が0になることを回避するために極めて小さい値を与えている。

4. 勾配降下法

概要

深層学習の目的は、学習を通して誤差関数を最小にするネットワークを作成することです。
つまり、誤差$E(w)$を最小化するパラメータ$w$を発見することになります。
これは、勾配降下法を利用してパラメータを最適化することで実現します。

• 勾配降下法
  $$
  W^{(t+1)}=W^t-\epsilon\Delta E　　\epsilon\text{は学習率}
  $$

$$
\quad \nabla E = \frac{\partial E}{\partial W} = \Bigl[\frac{\partial E}{\partial w_1}…\frac{\partial E}{\partial w_M}\Bigl]
$$

学習率の値によって学習の効率は大きく異なります。
学習率が大きすぎた場合、最小値にいつまでもたどりつかず発散してしまいます。
学習率が小さい場合、発散することはないですが、小さすぎると収束するまでに時間が掛かってしまいます。

• 確率的勾配降下法（SGD）
  $$
  W^{(t+1)}=W^{(t)}-\epsilon\nabla{E_n}
  $$

$$
\quad \nabla E = \frac{\partial E}{\partial W} = \Bigl[\frac{\partial E}{\partial w_1}…\frac{\partial E}{\partial w_M}\Bigl]
$$

勾配降下法が全サンプルの平均誤差を計算していたのに対して、確率的勾配降下法はランダムに抽出したサンプルの誤差を用います。
メリットとしては、データが冗長な場合の計算コストの軽減、望まない局所極小値解に収束するリスクの軽減、オンライン学習ができること等があげられます。

SGDの実装例は次のようになります。

SGDの実装例

class SGD:
    def __init__(self, learning_rate=0.01):
        self.learning_rate = learning_rate

    def update(self, params, grad):
        for key in params.keys():
            params[key] -= self.learning_rate * grad[key] 

SGDのハイパーパラメータは学習率ϵ（self.learning_rate）です。このパラメータをによって学習の効率は大きく異なります。

• ミニバッチ勾配降下法
  $$
  W^{(t+1)}=W^{(t)}-\epsilon\nabla{E_t}
  $$
  $$
  E_t=\frac{1}{N_t}\sum_{n \in D_t}{E_n}
  $$
  $$
  N_t=|D_t|
  $$

ミニバッチ勾配降下法は、ランダムに分割したデータの集合（ミニバッチ）$D_t$に属するサンプルの平均誤差です。
確率的勾配降下法のメリットを損なわずに、計算機の計算資源を有効活用できます。例えば、CPUを利用したスレッド並列化やGPUを利用したSIMD並列化をすることができます。

確認テスト

確認テスト1

「1_3_stochastic_gradient_descent.ipynb」から勾配降下法の下記数式に該当するコードを抜き出せ。

W^{t+1}=W^{t}-\epsilon\Delta{E}

解答：

network[key] -= learning_rate * grad[key]

確認テスト2

オンライン学習とは何か？

解答：

学習データが入ってくるたびに都度パラメータを更新し、学習を進めていく方法。一方、バッチ学習では一度にすべての学習データを使ってパラメータ更新を行う。

確認テスト3

下記の数式の意味を図に書いて説明せよ。

w^{t+1}=w^{t}-\epsilon\Delta{E}

解答：

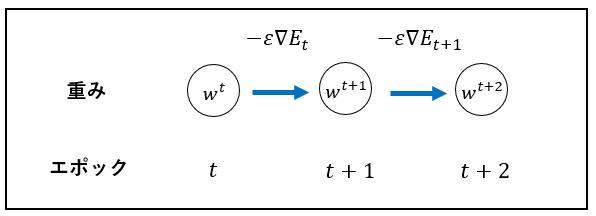
前のエポックの誤差を元に重みを修正（学習）していくことによって、データに適合した予測ができるようになっていく。

5. 誤差逆伝播法

概要

勾配降下法の誤差勾配の計算を各パラメータに対して数値微分で計算しようとすると、順伝播の計算を繰り返し行う必要があるため、負荷が大きくなります。
この問題を解決する方法が誤差逆伝播法になります。

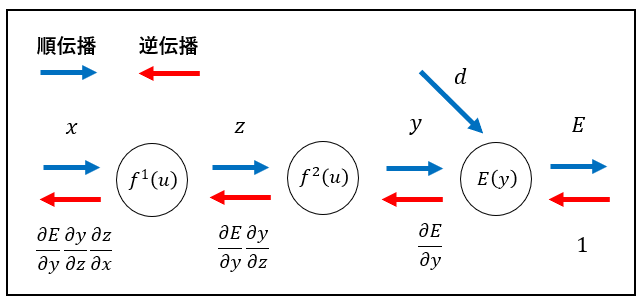
誤差逆伝播法では、算出された誤差を出力層側から順に微分し、前の層へと伝播させていきます。
最小限の計算で各パラメータの数値微分を解析的に計算することができます。

コード実装

誤差逆伝播法をnumpyで実装しました。
コードが少し長くなってしまったので、詳細はgithubをご覧ください。
重みが更新されていく様子を確認できると思います。
github：誤差逆伝播法のコード実装

確認テスト

確認テスト1

誤差逆伝播法では不要な再帰的処理を避ける事が出来る。
「1_3_stochastic_gradient_descent.ipynb」から既に行った計算結果を保持しているソースコードを抽出せよ。

解答：

# 誤差逆伝播
def backward(x, d, z1, y):
    # print("\n##### 誤差逆伝播開始 #####")    

    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    # 出力層でのデルタ(誤差関数を微分したもの)
    delta2 = functions.d_mean_squared_error(d, y)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 中間層でのデルタ
    #delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)

    ## 試してみよう
    # 誤差関数を微分した結果を前の層の計算にも使って戻していっている。
    delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)

    delta1 = delta1[np.newaxis, :]
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    x = x[np.newaxis, :]
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
    
    # print_vec("偏微分_重み1", grad["W1"])
    # print_vec("偏微分_重み2", grad["W2"])
    # print_vec("偏微分_バイアス1", grad["b1"])
    # print_vec("偏微分_バイアス2", grad["b2"])

    return grad

確認テスト2

以下の2つの数式に該当するソースコードを探せ。

数式1：

\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}

解答：

delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)

数式2：

\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\frac{\partial u}{\partial w_{ji}^{(2)}}

解答：

grad['W1'] = np.dot(x.T, delta1)

参考にした書籍

本記事を作成するにあたって以下の書籍を参考にしました。
非常にわかりやすく理解が深まりました。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
[[第3版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践]
(https://www.amazon.co.jp/%E7%AC%AC3%E7%89%88-Python%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E9%81%94%E4%BA%BA%E3%83%87%E3%83%BC%E3%82%BF%E3%82%B5%E3%82%A4%E3%82%A8%E3%83%B3%E3%83%86%E3%82%A3%E3%82%B9%E3%83%88%E3%81%AB%E3%82%88%E3%82%8B%E7%90%86%E8%AB%96%E3%81%A8%E5%AE%9F%E8%B7%B5-impress-gear/dp/4295010073/ref=asc_df_4295010073/?tag=jpgo-22&linkCode=df0&hvadid=342595526565&hvpos=&hvnetw=g&hvrand=15773796937735192064&hvpone=&hvptwo=&hvqmt=&hvdev=c&hvdvcmdl=&hvlocint=&hvlocphy=1009283&hvtargid=pla-934396349943&psc=1&th=1&psc=1)