フィンガープリントを可視化してみる～TopologicalTorsionFingerprint～

はじめに

こちらの続き。

前回の AtomPairFingerprint に続き、今回はさらに情報の少ないTopologicalTorsionFingerprintの可視化方法を検討したので共有したい。

#TopologicalTorsionFingerprintとは？
端的にいうと二面角に関するフィンガープリントだ。

二面角についてはこちらの定義を参照してほしい。
https://www.weblio.jp/wkpja/content/%E4%BA%8C%E9%9D%A2%E8%A7%92_%E5%8C%96%E5%AD%A6

フィンガープリントについては RDKitでフィンガープリントを使った分子類似性の判定 を見てほしい(またも丸投げ)

本記事の目的

本記事では、TopologicalTorsionFingerprintのビットとして「4303634976 」のようなコードが与えられたときに、そのコードが化合物のどの部分に該当するのかを可視化する方法をお伝えすることである。

#環境

• RDKit 2021.09.2
• cairosvg

#やり方

準備

例えば、

from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Descriptors, Draw
from rdkit.ML.Descriptors import MoleculeDescriptors
from rdkit.Chem.AtomPairs import Torsions

tt = Torsions.GetTopologicalTorsionFingerprint(mol)
for torsion in tt.GetNonzeroElements().keys():
    print(torsion, '\t', Torsions.ExplainPathScore(torsion), tt.GetNonzeroElements()[torsion])

のように、分子のTopologicalTorsionFingerprintを計算し、ExplainPathScore関数を使うと、

4303634976 	 (('C', 1, 0), ('C', 3, 0), ('C', 3, 0), ('C', 1, 0)) 1
4437590049 	 (('C', 2, 0), ('C', 2, 0), ('C', 2, 0), ('C', 2, 0)) 1
4437590560 	 (('C', 1, 0), ('C', 3, 0), ('C', 2, 0), ('C', 2, 0)) 2
4437852704 	 (('C', 1, 0), ('C', 3, 0), ('C', 3, 0), ('C', 2, 0)) 2
4437852705 	 (('C', 2, 0), ('C', 3, 0), ('C', 3, 0), ('C', 2, 0)) 1
4571807777 	 (('C', 2, 0), ('C', 2, 0), ('C', 2, 0), ('C', 3, 0)) 2
4572069921 	 (('C', 2, 0), ('C', 2, 0), ('C', 3, 0), ('C', 3, 0)) 2

のように、分子に含まれるTopologicalTorsionFingerprintのビットを表す各コードについて、それがどのような4つの原子コードから構成されているかを得ることができる。

4つの原子コードの内、真ん中の2つが、2組の3原子が共有する2原子と考えられるので、この真ん中の2つと分子中の全結合における両端の原子のコードを照合し、一致結合があった場合、1,4番目の原子コードと、結合の両端の原子それぞれの1つ先の原子のコードとを照合することで、コードに対応する二面角を構成する4原子を容易に特定できるのである。

実装コード

以下はkey「4303634976」に該当する二面角を構成する4原子を特定し、そのインデックス番号の一覧をresutlsに格納する処理である。molには可視化対象のRDKitのMOLオブジェクトが格納されている前提としている。
結果が複数ある場合もあるため、resutls　はリストのリストになっている。

key = 4303634976 
explained = Torsions.ExplainPathScore(key)

results = set()

# 全結合でループ
for i, bond in enumerate(mol.GetBonds()):
    #print(f"=={i}==")
    # 結合の両端の原子を取得
    atom1 = bond.GetBeginAtom()
    atom2 = bond.GetEndAtom()
    
    # 結合の両端の原子コードを取得
    explain1 = Utils.ExplainAtomCode(Utils.GetAtomCode(atom1))
    explain2 = Utils.ExplainAtomCode(Utils.GetAtomCode(atom2))
    
    # 結合の両端の原子が、explainの真ん中の2つの結合に一致する場合(ケース1)
    # 　atom1, 2の順にexplained[1], explained[2]とマッチした場合
    if (explain1 == explained[1]) and (explain2 == explained[2]):
        # atom1の結合の反対側の原子とexplain0を比較
        atom0s = []
        for tmpBond in atom1.GetBonds():
            if bond.GetIdx() != tmpBond.GetIdx():
                atom0 = tmpBond.GetOtherAtom(atom1)
                explain0 = Utils.ExplainAtomCode(Utils.GetAtomCode(atom0))
                if explain0 == explained[0]:
                    atom0s.append(atom0.GetIdx())

        # atom2の結合の反対側の原子とexplain3を比較                    
        atom3s = []
        for tmpBond in atom2.GetBonds():
            if bond.GetIdx() != tmpBond.GetIdx():
                atom3 = tmpBond.GetOtherAtom(atom2)
                explain3 = Utils.ExplainAtomCode(Utils.GetAtomCode(atom3))
                if explain3 == explained[3]:
                    atom3s.append(atom3.GetIdx())
        
        # 全ての原子の組合わせにより結果を生成
        for atom0_idx in atom0s:
            for atom3_idx in atom3s:     
                result = (atom0_idx, atom1.GetIdx(), atom2.GetIdx(), atom3_idx)
                result2 = tuple(sorted(result))
                results.add(result2)
        
    # 結合の両端の原子が、explainの真ん中の2つの結合に一致する場合(ケース2)        
    # 　atom2, 1の順にexplained[1], explained[2]とマッチした場合    
    if (explain2 == explained[1]) and (explain1 == explained[2]):
        # atom2の結合の反対側の原子とexplain0を比較
        atom0s = []
        for tmpBond in atom2.GetBonds():
            if bond.GetIdx() != tmpBond.GetIdx():
                atom0 = tmpBond.GetOtherAtom(atom2)
                explain0 = Utils.ExplainAtomCode(Utils.GetAtomCode(atom0))
                if explain0 == explained[0]:
                    atom0s.append(atom0.GetIdx())

        # atom1の結合の反対側の原子とexplain3を比較                    
        atom3s = []
        for tmpBond in atom1.GetBonds():
            if bond.GetIdx() != tmpBond.GetIdx():
                atom3 = tmpBond.GetOtherAtom(atom1)
                explain3 = Utils.ExplainAtomCode(Utils.GetAtomCode(atom3))
                if explain3 == explained[3]:
                    atom3s.append(atom3.GetIdx())
        
        # 全ての原子の組合わせにより結果を生成
        for atom0_idx in atom0s:
            for atom3_idx in atom3s:     
                result = (atom0_idx, atom2.GetIdx(), atom1.GetIdx(), atom3_idx)
                result2 = tuple(sorted(result))
                results.add(result2)

results = list(results)
print(results)      

これを実行すると次のように、results変数に「4303634976 」に該当する二面角を構成する4原子のリストが複数分格納される。

[(0, 1, 6, 7)]

該当箇所の原子が特定できたため、これを可視化してみよう。まず、可視化関数を用意する。

from rdkit.Chem.Draw import rdMolDraw2D
from IPython.display import SVG
from io import BytesIO
from PIL import Image
from cairosvg import svg2png

def generate_image(mol, highlight_atoms, size, isNumber=False):

    view = rdMolDraw2D.MolDraw2DSVG(size[0], size[1])
    tm = rdMolDraw2D.PrepareMolForDrawing(mol)
    
    option = view.drawOptions()    
    if isNumber:
        for atom in mol.GetAtoms():
            option.atomLabels[atom.GetIdx()] = atom.GetSymbol() + str(atom.GetIdx() + 1)    
    
    view.DrawMolecule(tm, highlightAtoms=highlight_atoms)
    view.FinishDrawing()
    svg = view.GetDrawingText()
    SVG(svg.replace('svg:', ''))
    ret = svg2png(bytestring=svg.encode('utf-8'))
    img = Image.open(BytesIO(ret))
    return img

次に、上の関数にresultsの0番目のリストを与えて可視化してみる。

img = generate_image(mol, results[0], (400,200), True)
img 

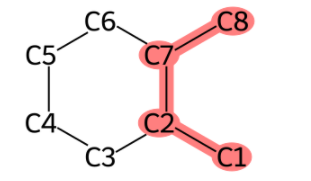
Jupyter Labであればこんな感じで表示されるはずだ。

これにより当該のリストが、ハイライトされている部分の2面角を示していることが一目に分かる。
同様にresults内の全リストについて色を変更する等して可視化すれば、分子中における「4303634976」に該当する全2面角を一目で表示させることができるはずだ。

#おわりに
今回、ロジックが複雑になってしまったが、RDkitの機能を使えばもっと楽ができそうな気がする。
もっとRDKitついて勉強せねば。