2次元ブラウン運動シミュレーション

この記事は フリュー Advent Calendar 2024の11日目の記事になります。

目次

• 背景
• 目的
• 理論的概要
  • ランダムウォークとモンテカルロ
  • ランダムワークモンテカルロ法の長所と短所
• 実装
  • 変数設定
  • 粒子の位置をランダムで更新
  • 各粒子の移動経路可視化
  • 時間に伴う移動距離と統計的な解析
  • 各ステップごとの平均位置と分散を計算
• シミュレーション結果
• 結論

背景

ブラウン運動は、液体や気体中で微小な粒子が無作為に動く現象であり、自然界や工学分野において広く観察される基本的な物理現象です。この現象は、1827年にロバート・ブラウンによって観察され、粒子が周囲の分子から受ける衝突によって引き起こされるランダムな運動として理解されています。ブラウン運動の理解は、統計力学や確率論の基礎を深めるだけでなく、材料科学、生物物理学、金融工学など多岐にわたる応用分野にも重要な影響を与えます。また、ブラウン運動はランダムウォークの数学的モデルとしても位置づけられ、確率過程の研究においても重要な役割を果たしています。

目的

本記事の目的は、モンテカルロ法を用いて多数の粒子が2次元空間でどのように動くかをシミュレーションし、その結果を可視化することで、ブラウン運動の特性を直感的に理解することです。具体的には、ランダムウォークモデルを基にしたシミュレーションを実装し、粒子の移動経路や統計的特性（平均位置、分散など）を解析することで、理論的な予測との整合性を確認します。さらに、シミュレーション結果を表示することで、ブラウン運動のランダム性と拡散性を明確に示します。

理論的概要

ランダムウォークとモンテカルロ

ブラウン運動は、粒子の無作為な動きを表現するためのランダムウォークモデルとして数学的に定式化されます。ランダムウォークは、各ステップで粒子がランダムな方向に一定の距離を移動する過程を示します。2次元ランダムウォークでは、粒子が2次元平面上で無作為に移動し、その位置は確率的に変化します。モンテカルロ法は、このランダムウォークを多数の粒子に適用し、統計的な特性を解析するための強力なツールとして利用されます。特に、ブラウン運動の拡散性や自己相関の解析において、モンテカルロシミュレーションは理論的予測を補完する重要な手法です。

ランダムワークモンテカルロ法の長所と短所

長所としては、シンプルな実装が挙げられます。ランダムウォークのシミュレーションは、比較的容易に実装でき、基本的な確率論と数値計算の知識があれば誰でも取り組むことができます。

短所としては、計算コストが挙げられます。粒子数やステップ数が増加すると、計算量も急激に増大します。

実装

変数設定

先ずは、シミュレーションに必要な主要なパラメータを設定します。ここでは、100個の粒子を500ステップにわたってシミュレーションします。そして、モデルの単純化のため温度、気圧などが場所によって変わらない安定的な環境で粒子運動すると想定し、各ステップで粒子がランダムの方向で1ユニットごとに移動するように設定しました。

# シミュレーションパラメータ
num_particles = 100  # Number of particles
num_steps = 500      # Number of simulation steps
step_size = 1        # Step size (average distance per step)

粒子の位置をランダムで更新

各粒子の位置を保存する配列を初期化し、各ステップごとにランダムな角度を生成します。次に、生成された角度に基づいてxおよびy方向の移動距離を計算し、累積和を取ることで各粒子の位置を更新します。

import numpy as np

# ランダムウォークシミュレーション
# 各粒子の位置を保存する配列を初期化（粒子数 x ステップ数 x 座標）
positions = np.zeros((num_particles, num_steps, 2))

# ランダムな角度を生成（0以上 ~ 2π未満）
angles = np.random.uniform(0, 2*np.pi, size=(num_particles, num_steps))

# xおよびy方向の移動距離を計算
dx = step_size * np.cos(angles)
dy = step_size * np.sin(angles)

# 各粒子の位置を更新
positions[:, 1:, 0] = np.cumsum(dx, axis=1)[:, :-1]
positions[:, 1:, 1] = np.cumsum(dy, axis=1)[:, :-1]

各粒子の移動経路可視化

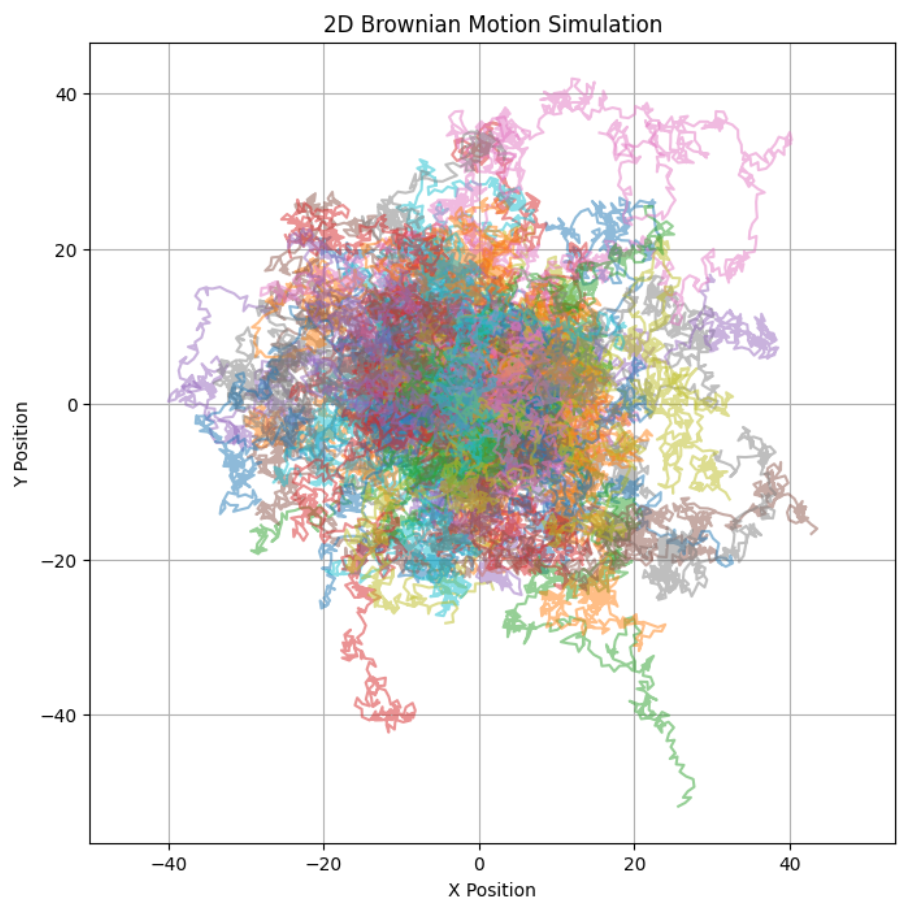
次は、ランダムで500ステップ移動した粒子の移動経路をプロットしてみました。
上で計算した配列をプロットすることで可視化できます。

import matplotlib.pyplot as plt

# 可視化の設定
plt.figure(figsize=(8, 8))
plt.title('2D Brownian Motion Simulation')
plt.xlabel('X Position')
plt.ylabel('Y Position')

# 各粒子の経路を描画
for i in range(num_particles):
    plt.plot(positions[i, :, 0], positions[i, :, 1], alpha=0.5)

plt.grid(True)
plt.axis('equal')
plt.show()

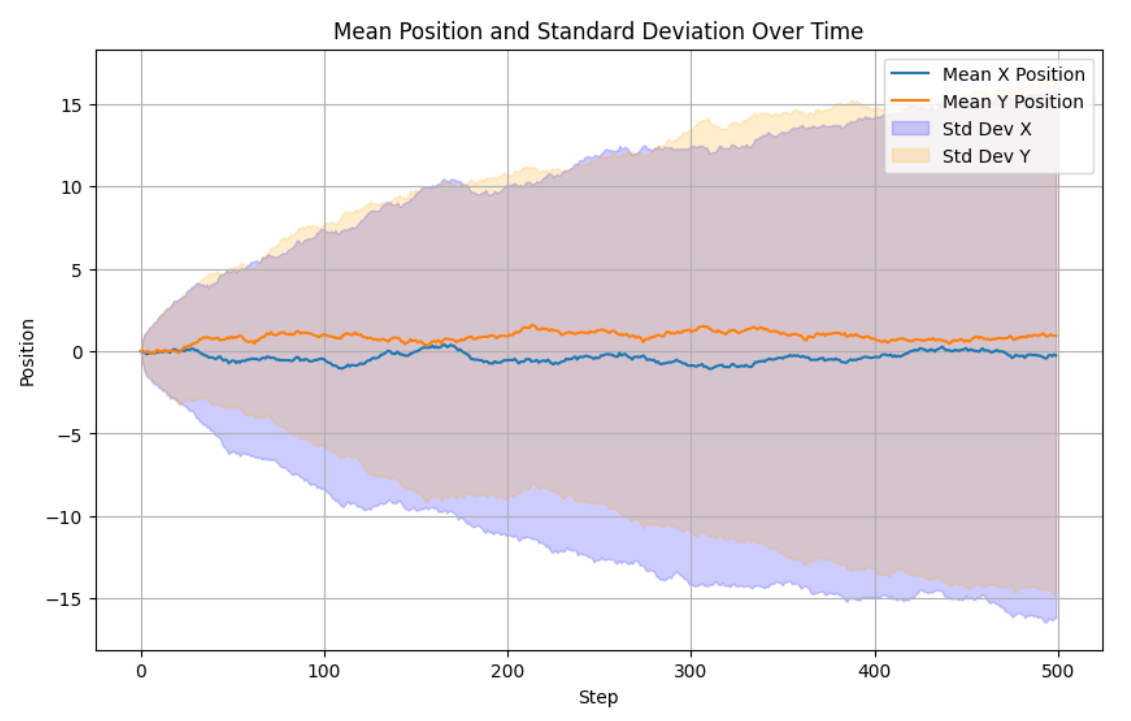
時間に伴う移動距離と統計的な解析

次に、粒子が時間とともにどのように分布するかを分析しました。各ステップごとに粒子の平均位置と標準偏差を計算し、それらをプロットすることで分布の変化を視覚化できます。

各ステップごとの平均位置と分散を計算

mean_positions = np.mean(positions, axis=0)  # ステップ数 x 2
std_positions = np.std(positions, axis=0)    # ステップ数 x 2

#### 可視化
plt.figure(figsize=(10,6))
plt.plot(mean_positions[:, 0], label='Mean X Position')
plt.plot(mean_positions[:, 1], label='Mean Y Position')
plt.fill_between(range(num_steps), 
                 mean_positions[:, 0] - std_positions[:, 0],
                 mean_positions[:, 0] + std_positions[:, 0],
                 color='blue', alpha=0.2, label='Std Dev X')
plt.fill_between(range(num_steps), 
                 mean_positions[:, 1] - std_positions[:, 1],
                 mean_positions[:, 1] + std_positions[:, 1],
                 color='orange', alpha=0.2, label='Std Dev Y')
plt.title('Mean Position and Standard Deviation Over Time')
plt.xlabel('Step')
plt.ylabel('Position')
plt.legend()
plt.grid(True)
plt.show()

結果を分析すると、粒子の移動経路がランダムに分散している様子が確認できます。粒子数が多いほど、全体的な分布がより均一になり、平均位置はほぼ原点付近に留まることがわかります。これは、ランダムな移動方向が均等に分布しているため、全体としての平均位置がゼロに近づきます。一方、標準偏差は時間とともに増加しており、これは粒子が徐々に広範囲に分散していることを示しています。

シミュレーション結果

アニメーションを通じて、粒子がリアルタイムでどのように移動しているかを視覚的に確認でき、ブラウン運動のランダム性と拡散性を直感的に理解するのに役立ちます。

# アニメーションの作成
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(np.min(positions[:,:,0])-10, np.max(positions[:,:,0])+10)
ax.set_ylim(np.min(positions[:,:,1])-10, np.max(positions[:,:,1])+10)
ax.set_title('2D Brownian Motion Animation')
ax.set_xlabel('X Position')
ax.set_ylabel('Y Position')
ax.grid(True)

# 粒子の初期位置
scat = ax.scatter(positions[:,0,0], positions[:,0,1], alpha=0.6)

def update(frame):
    scat.set_offsets(positions[:, frame, :])
    return scat,

# アニメーションの作成
ani = FuncAnimation(fig, update, frames=num_steps, interval=30, blit=True)

# アニメーションをGIFとして保存
ani.save('brownian_motion.gif', writer=PillowWriter(fps=30))

plt.show()

結論

本シミュレーションでは、モンテカルロ法を用いた2次元ブラウン運動のシミュレーションを実施し、その結果を解析しました。これにより、粒子のブラウン運動をモンテカルロ法で可視化する方法を学びました。

モンテカルロ法は、本記事で作成したシンプルなモデルから複雑なシステムまで、様々な分野で有用に活用されます。2次元ブラウン運動のシミュレーションはその一例に過ぎませんが、基本的な手法や考え方を習得することで、より高度なシミュレーションや解析にも応用することが可能です。

以上、ありがとうございました！