この記事は、R Advent Calendar 2016の10日目の記事です。
昨日はcallmekohei様のR言語を使ってロト6を当ててみる!でした。
intro
その昔、昆虫少年?だった時代は、$Amarygminae$という連中を相手にしていました。
上位分類が$Tenebrionidae$と言いまして、日本語ではゴミムシダマシと呼びます。
この他にも、カミキリモドキ、ニセマグソコガネとか、そーゆーのが大好きでした。
この系統の名前で文句無しのチャンピオンは、ニセハムシダマシでしょうね。
ハムシも、それに似たハムシダマシもちゃんといます。
ハムシダマシに似て非なるムシを見つけちゃったから、ニセハムシダマシ。
ちなみに、ハムシモドキという連中もいますが、
寡聞にして、ニセハムシモドキの存在は知りません。
ふふふ
オトナダマシ
えーと、何でしたっけ。
そう。
人前でプレゼンテーションをする機会、結構ありますよね。(ね!!)
そんな時に、ぐるぐる回ったり、ぐりぐり動いたり、モノスゴクカラフルだったり、そんなFigureを皆さん出されますよね。でも、実際のデータ分析において、3Dプロットを書いて凄く研究が進むのか?、ぐりぐり動かせると論文が書けるのか?と言われると、まぁ、無いと思いますね。
こうしたFigureが役に立つのは、緻密な論理を積み重ねて説明する場面ではなく、短時間で概要を直感的に理解してもらう(理解した気になってもらう)場面なので、通称、オトナダマシ、です。
今回は、微分方程式を分かったふりをする、というオトナダマシです。
そう言えば去年のRアドカレに書いた記事も動画でピカピカ系でした。
力学系 dynamical system
今回の教科書は、『生物リズムと力学系』です。(主に2章)
力学系という用語がキーワードですが、定義を引用(p.14)しておきます。
時間発展するありとあらゆる対象は力学系(dynamical systems)と呼ばれる. 力学系という日本語を聞くと力学の一種に感じるかもしれないが、英語からわかる通り時間発展するもの一般を取り扱う広い枠組みである.
時間発展する現象を数理的に記述する。
これは$T_n$から$T_{n+1}$の変化の法則を書き下す事になります。
オトナダマシの記事なので、厳密な定義は他に譲るとしますが、
$f(x)$を連続な関数として、未知関数$x=x(t)$について、
\frac{dx}{dt}=f(x)\tag{1}
というような、時間微分関数で現象を記述する数理モデル一般というイメージです。
右辺が従属変数$x$のみで表される方程式を自律系と呼びます。
今回は、いくつかの自律系の時間発展を**ヴィジュアライズ(笑)**する事で、分かったふりをしましょう。
packages
今回は、この3つを使いました。
全てinstall.packages("hoge")で落とせます。
コードをなぞる際は、事前にlibrary("hoge")でアクティベートしておきましょう。
{deSolve}: 今回のメイン。
{rgl}: お絵かき用です。
{animation}: ImageMagicが必要になります。
バージョン情報等詳細は、Appendixにて。
単純な例から
式(1)の最高にシンプルな例は、
\frac{dx}{dt}=kx
ですが、**ヴィジュアライズ(笑)**的にはもう少し複雑にして、
\frac{dx}{dt}=kx(1-x)\tag{2}
を考えます。
Rで微分方程式を解くためのパッケージが**{deSolve}**です。
まずは式(2)を決まった様式で書き下した関数を定義します。
X <- function(t, state, parameters){
with(as.list(c(state, parameters)),{
dx <- k*x*(1-x)
list(c(dx))
})
}
で、パラメータの値と時間軸と初期値を設定します。
parameters <- c(k=1)
times <- seq(0, 10, by=0.2)
initial <- c(x=0.5)
で、ドドンっと解いてしまいます。
out <- ode(y = initial, times = times, func = X, params = parameters)
もう、そのままplotでいけます。
plot(out)

計算できてそうですね。でも、これではダマせない。
そこで、オトナダマシ的にはですね、ゴジョゴジョやって…

こんな感じでしょうか。
出発地点(初期値)が$x_0<0$の時は、明らかに$⁻∞$に発散ですね。
$x_0=0$ならば、常に$x=0$
$x_0>0$ならば、$t→∞$の時、$x_∞→1$ですね。
え?式(2)から明らか?ええ。**ヴィジュアライズ(笑)**してみました。
このダマシ絵の書き方は、Appendixにて。
2変数の場合
ロトカ・ヴォルテラ方程式 Lotoka-Volterra equations
通称、喰うか喰われるか方程式です。
喰うチームXと、喰われるチームY (どっちでもいいですが)を考えて、その個体数変動を表現する数理モデルです。難しい話は教科書に譲ります。
教科書に習い、5つの正の実数$a, K, b, c, r$を用いて、書き下すと、
\begin{eqnarray}
\frac{dx}{dt}&=&a(1-x/K-by)x \\
\frac{dy}{dt}&=&(-r+cx)y \tag{3}
\end{eqnarray}
もう説明をすっ飛ばして、
X <- function(t, state, parameters){
with(as.list(c(state, parameters)),{
dx <- a * (1 - x/K - b*y)
dy <- (-r + c* x)*y
list(c(dx, dy))
})
}
parameters <- c(a = 1, K = 3, b = 0.2, r = 0.1, c = 0.05)
times <- seq(0, 100, 0.5)
initial <- c(x=3, y=1)
out <- ode(y = initial, times = times, func = X, parms = parameters)
plot(out)

お、平衡に落ちてそうですね。
で、エイや!!

どこを初期値に取っても、●の点に収束している様子がヴィジュアライズされましたね!
からの、ドォーン!!

喰う側も喰われる側も、そりゃぁ色々ありますわな。
酒は呑んでも呑まれるな(自戒)。
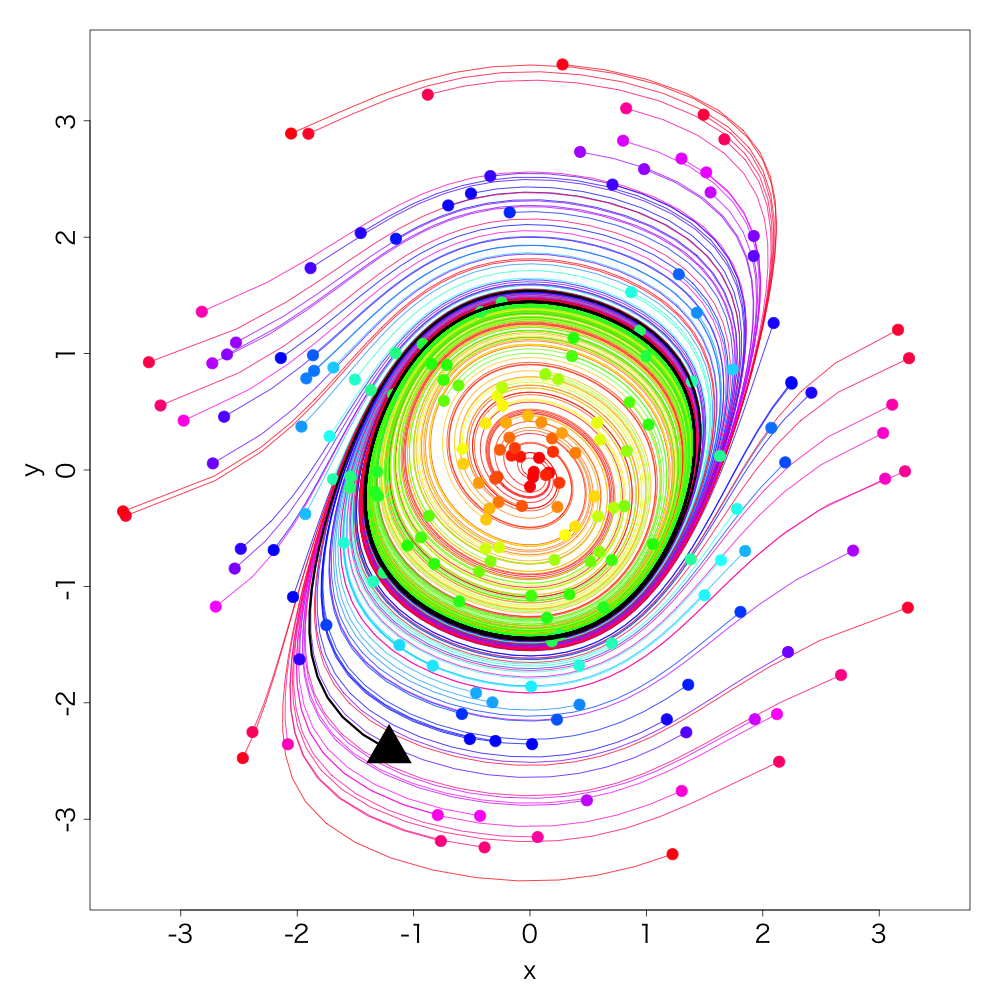
ファン・デア・ポル方程式 Van der Pol equations
電気回路の自励発振のモデル方程式、とか、そういう事は一切かまわず、
\begin{eqnarray}
\frac{dx}{dt}&=&ax+y-x^3/3\\
\frac{dy}{dt}&=&-x\tag{4}
\end{eqnarray}
よいしょ、
X <- function(t, state, parameters){
with(as.list(c(state, parameters)),{
dx <- a * x + y - x^3/3
dy <- -x
list(c(dx, dy))
})
}
times <- seq(0, 100, 0.1)
parameters <- c(a = 0.5)
initial <- c(x=3, y=1)
out <- ode(y = initial, times = times, func = X, parms = parameters)
からの、
plot(out)

おお。怪しい。
もう一声、
実にオトナダマシ感満載ですね。
こーゆー収束の仕方をリミットサイクルと呼びます。
酔っ払いトークは、リミットサイクルしないように気をつけましょう(自戒)。
最後はこれでしょう。
何も説明しないという暴挙。
いや、有名すぎて…。
それにしても美しい図形です(溜め息)。
X <- function(t, state, parameters){
with(as.list(c(state, parameters)),{
dx <- a*(y-x)
dy <- r*x-y-x*z
dz <- -b*z + x*y
list(c(dx, dy, dz))
})
}
parameters <- c(a = 10, b=8/3, r=40)
times <- seq(0, 200, 0.01)
initial <- c(x=0, y=0.1, z=0)
out <- ode(y = initial, times = times, func = X, parms = parameters)
Col <- colorRampPalette(c("#ff2800","#ff9900","#35a16b", "green"))
plot3d(out[,c("x", "y", "z")], type="n", box=F)
points3d(out[,c("x", "y", "z")], col=Col(length(times)))
このプロットを入れた.Rmdを{rmarkdown}で書きぃの、{knitr}で.html作りぃの、Githubに上げぇの、htmlPreviewでプレビューを出しぃの、さて、上手くリンク貼れたかどうか・・ここからどうぞ
グリグリして楽しんでください。
拡大縮小もできますよ。
あとがき
そういえば今回は、{ggplot2}を使わなかったです。
deSolve::odeの出力がdataframeではなくmatrixで出力されるためか、特に意識せずplotで書いちゃいました。
あ、そういえば{dplyr}も{tidyr}も出番がありませんでしたね。
Rアドカレのくせに...
ハドリヴァースの方角に43礼24拍37礼して、御神酒を備えておきますので許して下さい。
Enjoy!!
Appendix
環境
> sessionInfo()
R version 3.3.1 (2016-06-21)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: OS X 10.10.5 (Yosemite)
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] animation_2.4 rgl_0.96.0 deSolve_1.14
オトナダマシその1
# パッケージをアクティベート
library("deSolve")
# 微分方程式・初期値の設定
X <- function(t, state, parameters){
with(as.list(c(state, parameters)),{
dx <- k*x*(1-x)
list(c(dx))
})
}
parameters <- c(k = 1)
times <- seq(0, 10, 0.2)
# 初期値
N <- 100
x <- seq(0, 2, length=N)
# 微分方程式を解く
out <- NULL
for(i in 1:N){
initial <- c(x=x[i])
out[[i]] <- ode(y = initial, times = times, func = X, parms = parameters)
}
# ベクトル始点のY座標と角度
A <- seq(0, 2, by=0.1)
sita <- atan(A*(1-A))
# グラフィックスパラメータの準備
par(mgp=c(1.5, 0.3, 0), tcl=-0.2, mar=c(3,3,1,1))
# 画面の用意
plot(0,0, type="n", xlim=c(0, 10), ylim=c(0, 2), xlab="time", ylab="x")
# 矢印を書く。ゴリ押しです。もっと簡単にかけると思うけど…
for(i in 0:20){
for(j in 1:length(sita)){
if(0.4*abs(sin(sita[j])) < 0.1){
arrows(i/2, j*0.1-0.1, i/2 + 0.4*cos(sita[j]),
j*0.1 + 0.4*sin(sita[j])-0.1, length=0.15, col="darkgrey")
}else{
arrows(i/2, j*0.1-0.1, i/2 - 0.1*cos(sita[j])/sin(sita[j]),
j*0.1-0.2, length=0.15, col="darkgrey")
}
}}
# 線はカラフルにキめましょう。
for(i in 1:N){
lines(out[[i]], col=rainbow(N)[i])
}
オトナダマシその2
set.seed(1)
parameters <- c(a = 1, K = 3, b = 0.2, r = 0.1, c = 0.05)
X <- function(t, state, parameters){
with(as.list(c(state, parameters)),{
dx <- a * (1 - x/K - b*y)
dy <- (-r + c* x)*y
list(c(dx, dy))
})
}
# 始点の初期値。ここでちょっとバラつかせるのがオトナダマシ的テクニック
N <- 360
sita <- seq(0, 2*pi, length=N)
x <- 2 * cos(sita) + 2.1 +runif(N, 0, 0.5)
y <- 2 * sin(sita) + 2.1+runif(N, 0, 0.5)
times <- seq(0, 100, 0.5)
out <- NULL
for(i in 1:N){
initial <- c(x=x[i], y=y[i])
out[[i]] <- ode(y = initial, times = times, func = X, parms = parameters)
}
# 色はビカビカにキめよう。
plot(0, 0, xlim=c(0,4.5), ylim=c(0, 4.5), type="n", xlab="x", ylab="y")
for(i in 1:N)
lines(out[[i]][,2:3], col=rainbow(N)[i], lwd=1)
points(x,y, col=rainbow(N), pch=20, cex=1)
points(2, 5/3, pch=16, cex=1.5)
# 3dプロットはこんな感じ。
dat_x <- NULL
dat_y <- NULL
for(i in 1:N){
dat_x <- cbind(dat_x, out[[i]][,2])
dat_y <- cbind(dat_y, out[[i]][,3])
}
plot3d(0, 0, 0, xlim=c(0, 5), ylim=c(0,5), zlim=c(0,100), type="n", box=F,
xlab="x", ylab="y", zlab="")
points3d(dat_x[1,], dat_y[1,], rep(0, N), col=rainbow(N))
for(i in 1:N){
lines3d(dat_x[,i], dat_y[,i], times, col=rainbow(N)[i])
}
オトナダマシその3
set.seed(1)
# ここ大事
X <- function(t, state, parameters){
with(as.list(c(state, parameters)),{
dx <- a * x + y - x^3/3
dy <- -x
list(c(dx, dy))
})
}
# 準備
parameters <- c(a = 0.5)
N <- 200
times <- seq(0, 100, 0.1)
r <- seq(0, 3.5, length=N) + runif(N, 0, 0.1)
sita <- runif(N, 0, 2*pi)
x <- r * cos(sita)
y <- r * sin(sita)
Col <- rainbow(N)
# がんばる
out <- NULL
for(i in 1:N){
initial <- c(x=x[i], y=y[i])
out[[i]] <- ode(y = initial, times = times, func = X, parms = parameters)
}
# お絵かき
par(mgp=c(1.5, 0.3, 0), tcl=-0.2, mar=c(3,3,1,1))
plot(0, 0, xlim=c(-3.5, 3.5), ylim=c(-3.5, 3.5), type="n", xlab="x", ylab="y")
for(i in 1:N)
lines(out[[i]][,2:3], col=Col[i], lwd=1)
points(x,y, col=Col, pch=20, cex=1.5)
a <- sample(1:N,1)
lines(out[[a]][,2:3], lwd=3)
points(x[a], y[a], pch=17, cex=3)
dat_x <- NULL
dat_y <- NULL
for(i in 1:N){
dat_x <- cbind(dat_x, out[[i]][,2])
dat_y <- cbind(dat_y, out[[i]][,3])
}
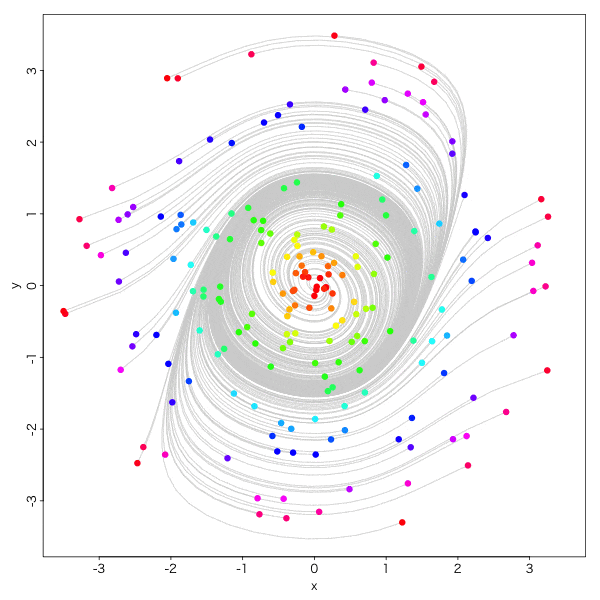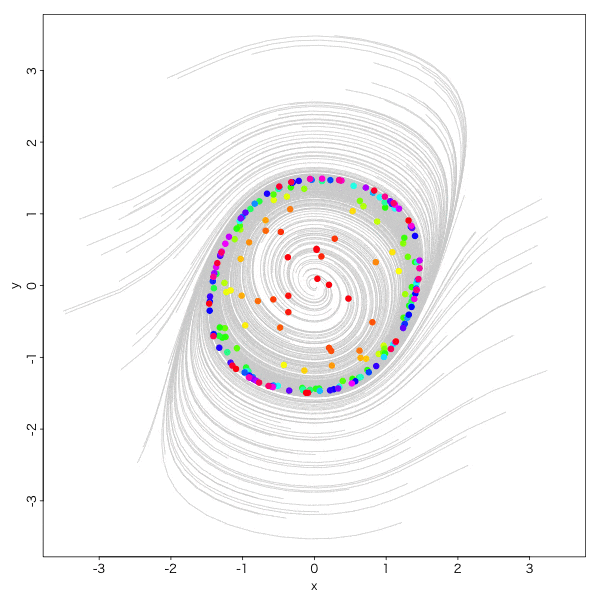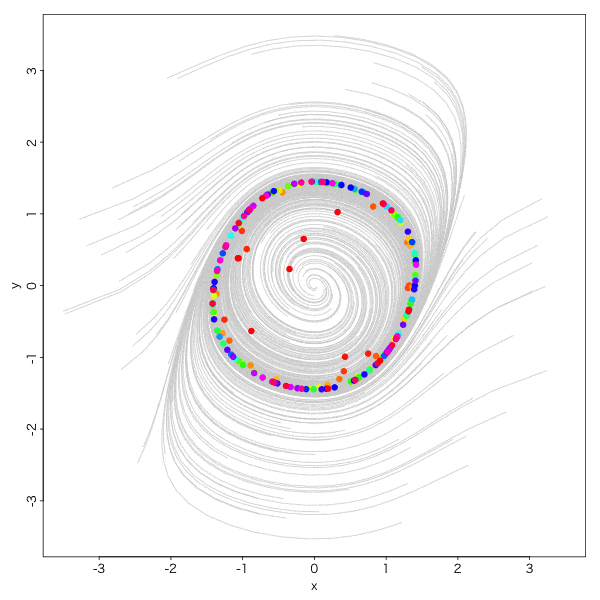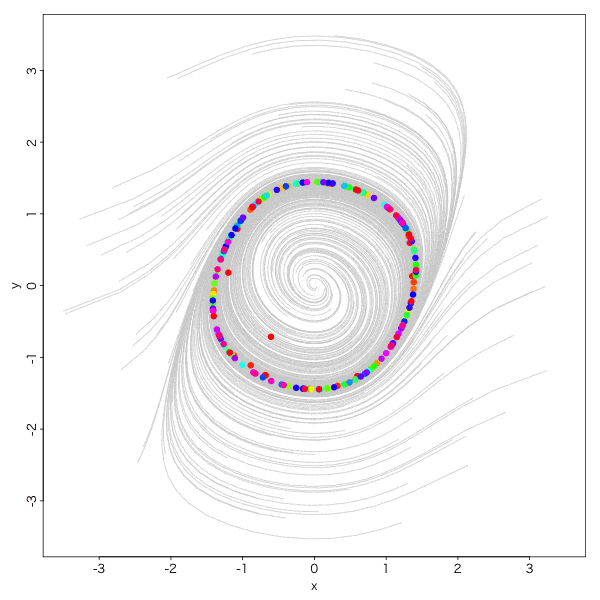
# {animation}です。
saveGIF({
ani.options(interval = 0.02,
convert = "/opt/ImageMagic/bin/convert")
# for(k in 1:length(times)){
for(k in 1:150){
par(mgp=c(1.5, 0.3, 0), tcl=-0.2, mar=c(3,3,1,1))
plot(0, 0, xlim=c(-3.5, 3.5), ylim=c(-3.5, 3.5), type="n", xlab="x", ylab="y")
for(i in 1:N){
lines(out[[i]][,2:3], col="lightgrey", lwd=1)
}
points(dat_x[k,], dat_y[k,], col=Col, pch=16, cex=1.2)
}},
movie.name = "VP1.gif",
ani.width=400, ani.height=400, clean=T
)