承前
・カーネルトリック
・R de 『カーネル多変量解析』
・R de 『カーネル多変量解析』-2
復習
$φ(x_i)φ(x_j)$の形で書ける関数はカーネル関数$k(x_i,x_j)$として扱え、
グラム行列$K$を求める事で、例えば無限の特徴量を考慮した近似が簡単に行えた。
(カーネルトリック)
これではまだ不便です。
前回に紹介したカーネル関数$k(x_i,x_j)$:ガウスカーネルと呼ばれます、や、それに対応する$φ(x)$は、空から降ってきたものです。
\begin{eqnarray}
k(x_i, x_j)&=&α\ \mathrm{exp}\left(-\beta\ ||x_i-x_j||^2\right)\tag{1}\\
φ(x)&=&\left(A\ \mathrm{exp}\left(-B(x-z)^2\right)\mid\ z\in\mathbb{R} \right) \tag{2}\\
\end{eqnarray}
このままだと、空から降ってきた特徴量ベクトルの内積を求めたり、空から降ってきた関数をなんらかの特徴ベクトルの内積に分解できるかを確かめないと、カーネル関数として使えない。
それは面倒。
カーネル関数が必ず満たす(かつ簡便に検証可能な)性質が明らかになれば、特徴量から離れて、いきなりカーネル関数かどうかを検証できる。
それが(半)正定値性と、再生性と呼ばれる性質。
再生性
内積の記号を少し変えます。
A^TB=\left<A,\ B\right>
特徴ベクトル$φ(x)$を、適当な関数$f$と任意の入力$\cdot$を用いて、
φ(x)=f(x,\ \cdot)
と表す時、カーネル関数は、特徴ベクトルの内積だから、
\begin{eqnarray}
k(x_i, x_j)&=&\left<φ(x_i),\ φ(x_j)\right>\\
&=&\left<f(x_i,\ \cdot),\ f(x_j,\ \cdot)\right>
\end{eqnarray}
関数$f$がカーネル関数$k$と一致する時、
\begin{eqnarray}
k(x_i, x_j)&=&\left<k(x_i,\ \cdot),\ k(x_j,\ \cdot)\right>\tag{3}\\
\end{eqnarray}
(3)をよく見ると、$g(x)=k(x_i,\ \cdot),\ x=x_j$として、
\begin{eqnarray}
g(x)&=&\left<g(\cdot),\ k(x,\ \cdot)\right>\tag{4}\\
&=&\left<g(\cdot),\ φ(x)\right>\tag{5}
\end{eqnarray}
この時、$φ(x)$が再生性を持つと言い、$φ(x)$を再生核と呼びます。
新しい関数$f'(x,\ \cdot)$を用意した時、カーネル関数として利用できるかどうかは、
再生性を持つかどうかで判断できる。
(※ ここではカーネル関数→再生核である事を示しており、
逆方向の証明:再生核→カーネル関数を割愛しています。)
正定値性
今、$φ(x)$が再生核であるとします。
ベクトル群$\left(φ(x_1),\ φ(x_2),...,\ φ(x_n)\right)$を基底とする空間中の任意の点$f(\cdot)$は、
\begin{eqnarray}
f&=&w_1φ(x_1)+w_2φ(x_2)+...+w_nφ(x_n)\\
&=&\sum_{i=1}^nw_i\ φ(x_i)\tag{6}
\end{eqnarray}
従って、任意の元$f(\cdot)$と$g(\cdot)$の内積は、再生性を用いて、
\begin{eqnarray}
\left<f(\cdot),g(\cdot)\right>
&=&\left<\sum_{i=1}^nα_i\ φ(x_i),
\sum_{i=1}^nβ_i\ φ(x_i)\right>\\
&=&\left<\sum_{i=1}^nα_i\ k(\cdot,x_i)
,\sum_{i=1}^nβ_i\ k(\cdot,x_i)\right> \\
&=&\sum_{i=1}^n\sum_{j=1}^nα_iβ_j\left<k(\cdot,\ x_i),\ k(\cdot,\ x_j)\right>\\
&=&\sum_{i=1}^n\sum_{j=1}^nα_iβ_j\ k(x_i,\ x_i) \tag{7}
\end{eqnarray}
ところで、内積は$≥0$をとるので、(7)右辺は正。
\sum_{i=1}^n\sum_{j=1}^nα_iβ_j\ k(x_i,\ x_i)≥0\tag{8}
グラム行列$K$の要素$k(x_i, x_j)$が式(8)を満たす時、
K=\left(k(x_i, x_j)\right)^n_{i, j=1}
=\left[\begin{array}{ccc}
k(x_1, x_1) & \ldots & k(x_1, x_n)\\
\vdots & \ddots & \vdots\\
k(x_n, x_1) & \ldots & k(x_n, x_n)\\
\end{array}
\right]\tag{9}
$K$が半正定値である、と言います。
という事は、
1. グラム行列$K$が正定値であれば、
2. その要素はカーネル関数$k(x_i, x_j)$として取り扱え、
3. カーネル関数$k$は再生性を満たすから計算楽勝。
こうしたカーネル関数を正定値カーネルと呼ぶ。
さらに言えば、
4. 正定値行列であれば上のロジックを満足するという事は、
5. 正定値性を崩さない範囲で行列$K$を$K'$に変換できれば、
6. いくらでも新しいカーネル関数が作り出せる。
正定値カーネルの変換
\begin{eqnarray}
k_{add}&=&k_1(x_i,x_j)+k_2(x_i,x_j)\\
k_{mul}&=&k_1(x_i,x_j)k_2(x_i,x_j)
\end{eqnarray}
2つの正定値カーネルの和$k_{add}$と積$k_{mul}$も正定値になる。
これを利用すると、
例えば、任意次元の$x$に対して、$x^Tx$は正定値である。
従って、定数加算・べき乗の変換を加えたカーネル関数
k(x_i,x_j)=(x_i^Tx_j+c)^p\tag{10}
は、正定値である。(多項式カーネルと呼ばれる)
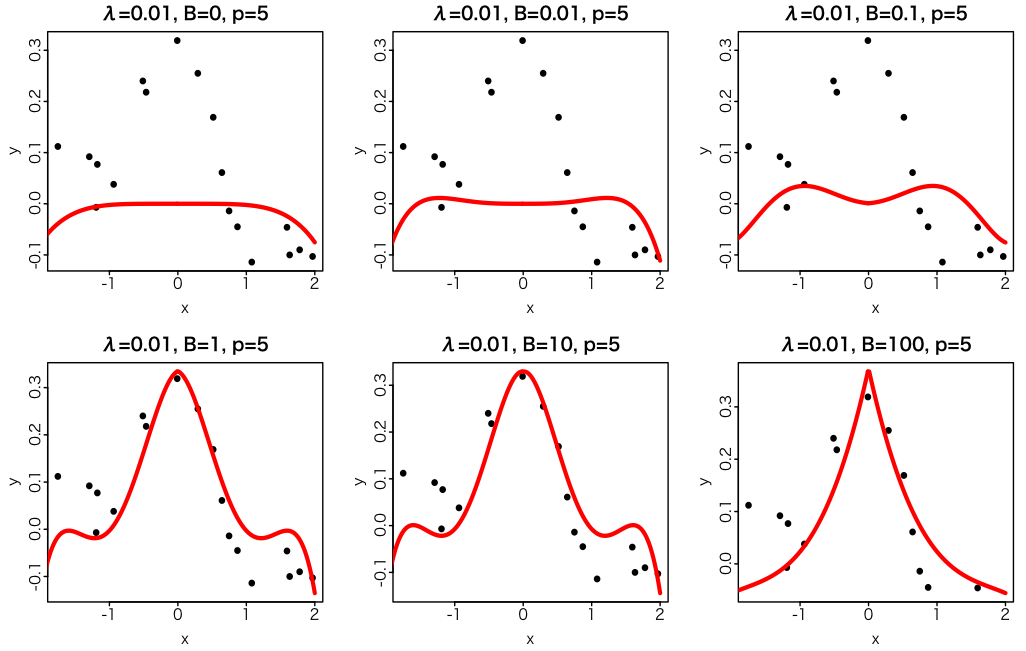
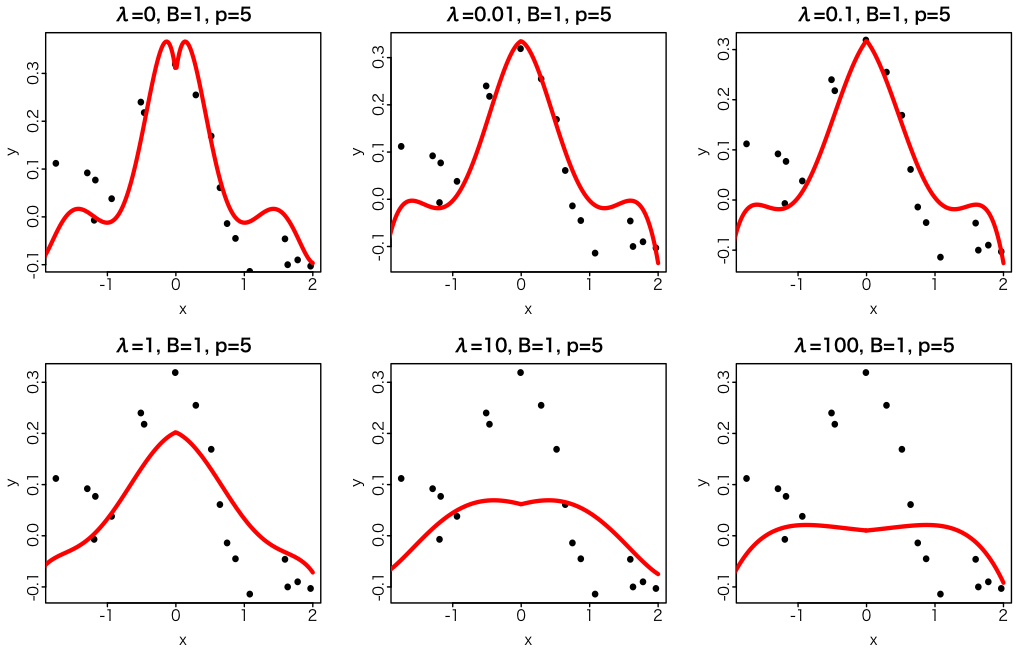
前々回のサンプルデータを用いて、
set.seed(1)
N <- 18
x <- runif(N,-2,2) # X座標
e <- rnorm(N, 0, 0.03) # 正規誤差
A <- 0.7 # 定義域の真ん中だけ凸にしたい
y <- rep(0, N)
y[abs(x)<A] <- -0.5*x[abs(x) < A]^2+0.3
y <- round(y -0.05*x + e, 3)

$p=5$として、
p <- 5
B <- 1
# Kを求める
K <- matrix(0, N, N)
for(i in 1:N)
for(j in 1:N)
K[i, j] <- (abs(x[i]*x[j])+B)^p
# 正規化項
lambda <- 0.01
w <- ginv(K+lambda*diag(N)) %*% t(y)
# predict
x_k <- seq(-2, 2, length=200)
y_k <- rep(0, length=200)
for(k in 1:200)
for(i in 1:N)
y_k[k] <- y_k[k]+w[i]*(abs(x[i]*x_k[k])+B)^p
あとはfor文でお絵描き。