ガウス過程まで行く予定が、カーネルトリックまでで1記事になってしまった…。
結果、話がまったく進まず。

承前
・R de 『カーネル多変量解析』
・R de 『カーネル多変量解析』-2

復習

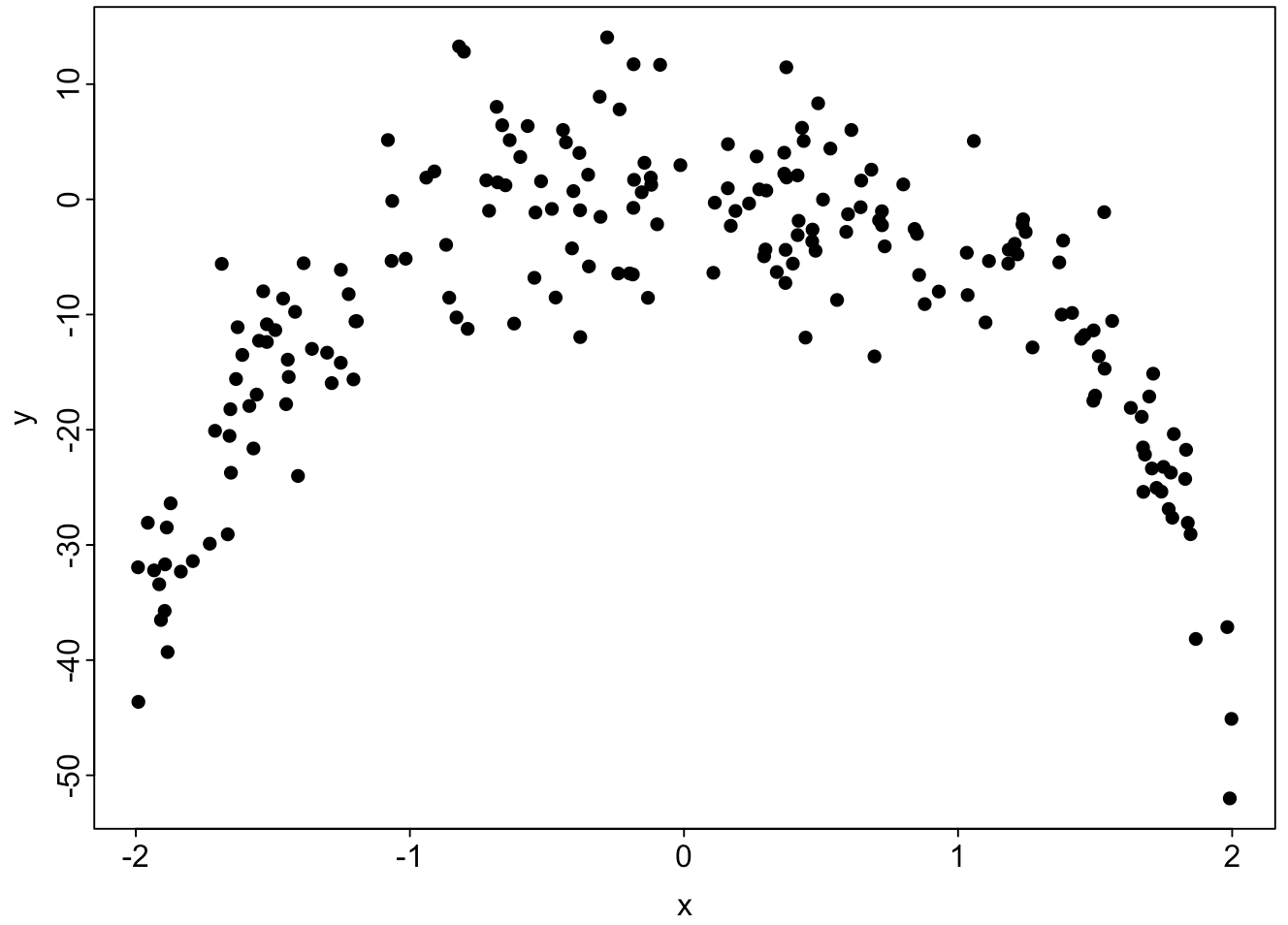
一次元の入力$X$に対する測定量$Y$が図のように得られた。

X=(X_1, X_2, ..., X_n)\\
Y=(Y_1, Y_2, ..., Y_n)

このデータから、任意の入力$x$に対する測定量$y$を導きたい。

y=f(x)

このためには２乗誤差が最小になる$f(x)$を求める。

\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\argmin_{f(x)}\ r_{square}=\sum_i^n \big(Y_i-f(X_i)\big)^2\tag{1}

$f(x)$を決定づけるパラメータを求めれば、$f(x)$は求まる。
これまでの議論から、特徴量空間の次元数$d$個のパラメータ$α$を推定すれば良い。

カーネル関数は、特徴ベクトルの内積として定義でき、
これを用いた近似ではデータ数$n$個のパラメータ$w$を推定する事になる。

\begin{eqnarray}
f(x)&=&\sum_{m=1}^d α_m\ φ_m(x) \tag{2}\\
&=&\sum_{i=1}^n w_i\ φ(X_i)^Tφ(x)\\
&=&\sum_{i=1}^n w_i\ k(X_i, x) \tag{3}\\
\end{eqnarray}

これをみると、(2)で考慮する特徴量$φ$の数が多ければ多いほど、(3)の方が有利だと分かる。

(1)(3)より、

\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\argmin_{w}\ r_{square}=\sum_j^n \big(Y_j-\sum_{i=1}^n w_i\ k(X_i, X_j)\big)^2\tag{4}

この$w$を求めればよい。

ここで$n×n$行列 $k(x_i, x_j)$をグラム行列$K$として、

K=\left(k(x_i, x_j)\right)^n_{i, j=1} 
=\left[\begin{array}{ccc}
k(x_1, x_1) & \ldots & k(x_1, x_n)\\
\vdots & \ddots & \vdots\\
k(x_n, x_1) & \ldots & k(x_n, x_n)\\
\end{array}
\right]\tag{5}

(4)(5)より、

\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\begin{eqnarray}
\argmin_{w}\ r_{square} &=& (Y-wK)^T(Y-wK)\\
w&=&(K^TK)^{-1}K^TY=K^{-1}Y\tag{6}
\end{eqnarray}

$K$が求まれば既知の$Y$から(1)を満たす$f(x)$を与える$w$が導ける。

ここまでは復習。

整理すると、
　　1.　$k$が求まる。
　　2.　$K$が求まる。　式(5)
　　3.　$w$が求まる。　式(6)　　
　　4.　$f(x)$が求まる。式(1)(3)

これまでの$k$の求め方は、
　　1-1. $d$個の特徴ベクトル$φ(x)$を定義する。
　　1-2. 全ての$x_i$について$φ(x_i)$を求める。
　　1-3. 特徴ベクトルの内積$k(x_i,x_j)=φ(x_i)^Tφ(x_j)$を求める。

これ、メンドーですよね。
一般に$d$は自明ではないですし、総当たり内積の計算コスト高いし。

例えば、例題のデータを多項式近似しようと思ったら次数をいくつにすれば良いか。
まぁ、偶関数なんでしょうけど、それ以上は分かりませんよね。
色々試してモデル選択、なんて考え出すと、はてしない物語になりかねない。

カーネルトリック

どうするのか。
$k(x_i, x_j)$は特徴ベクトル$φ(x_i)$と$φ(x_j)$で定義されていたので、

全てのk(x_i,x_j)は、φ(x_i)^Tφ(x_j)に変換できる。

これを逆立ちさせて、

φ(x_i)^Tφ(x_j)に変換できれば、全てk(x_i,x_j)。\tag{7}

と考えます。

例えば、前々回に紹介したカーネル関数、をジィーっと見つめます。

k(x_i, x_j)=α\ \mathrm{exp}\left(-\beta\ ||x_i-x_j||^2\right)\tag{8}

$x$を一次元として、特徴量ベクトル$φ(x)$を、

φ(x)=\left(A\ \mathrm{exp}\left(-B(x-z)^2\right)\mid\ z\in\mathbb{R} \right) \tag{9}\\

とします。
これは、無限個の実数$z$をあてはめた時の成分$φ_z(x)$の集合。

φ_z(x)=A\ \mathrm{exp}\left(-B(x-z)^2\right)\\

$φ_z(x)$同士の内積は、

φ_z(x_i)\ φ_z(x_j)=A^2\ \mathrm{exp}\left(-B(x_i-z)^2-B(x_j-z)^2\right)\\

$φ(x)$同士の内積にするために$z$について積分すると、

\begin{eqnarray}
φ(x_i)\ φ(x_j)
&=&\int_{-\infty}^{\infty}φ_z(x_i)\ φ_z(x_j)dz\\
&=&A^2\ \int_{-\infty}^{\infty}\mathrm{exp}\left(-B(x_i-z)^2-B(x_j-z)^2\right)\ dz\\
&=&A^2\sqrt{\frac{\pi}{2B}}\ \mathrm{exp}\left(-\frac{B}{2}(x_i-x_j)^2\right)\\
&=&α\ \mathrm{exp}\left(β(x_i-x_j)^2\right)\tag{A}\\

\end{eqnarray}

(8)の形になっている。

※ 式$(A)$の変形についてAppendixにて補足。(2019.09.18)

という事は、
・式(8)は$φ(x_i)^Tφ(x_j)$で書けるから、$k(x_i,x_j)$と見なして$K$が求まる。
・それは、無限の成分を持つ特徴ベクトル$φ(x)$を用いた近似と相同。
・無限個の$φ_z(x)$を求めて、全ての内積から$K$を求めるより遥かに楽。

どれぐらい楽かというと、たったn個のパラメータを推定するだけで、
無限の特徴量を考慮した回帰ができるぐらい楽。

もう、ものすごく楽なので、カーネルトリックと呼ばれています。

Rでの(ベタ打ち)実装は既に前々回でやっていますが、再掲。
$φ(x)$が姿を現さず、いきなり$k(x_i, x_j)$から計算が始まる(始められる)事に注意してください。

# サンプルサイズNのデータ(x, y)に対し、

# Kを求める
K <- matrix(0, N, N)
for(i in 1:N)
  for(j in 1:N)
    K[i, j] <- exp(-(x[i] - x[j])^2)

# 正規化項
lambda <- 0.01
w <- ginv(K+lambda*diag(N)) %*% t(y)

# predict
x_k <- seq(-2, 2, length=200)
y_k <- rep(0, length=200)
for(k in 1:200)
  for(i in 1:N)
    y_k[k] <- y_k[k]+w[i]*exp(-(x[i]-x_k[k])^2)

# plot
par(tcl=-0.2, mgp=c(1.5, 0.2, 0), mar=c(3,3,3,3))
plot(x,y, pch=16)
lines(x_k, y_k, col="Red", lwd=3)

Appendix

式$(A)$の変形について補足。(2019.09.18)

ガウス積分の公式

\int_0^{\infty}\mathrm{exp}\left[-ax^2\right]dx=\frac{1}{2}\sqrt{\frac{\pi}{a}}

より、

\int_{-\infty}^{\infty}\mathrm{exp}\left[-ax^2\right]dx=\sqrt{\frac{\pi}{a}}

これを使って、

\begin{eqnarray}
φ(x_i)\ φ(x_j)
&=&\int_{-\infty}^{\infty}φ_z(x_i)\ φ_z(x_j)dz\\
&=&A^2\ \int_{-\infty}^{\infty}\mathrm{exp}\left[-B(x_i-z)^2-B(x_j-z)^2\right]\ dz\\
&=&A^2\ \int_{-\infty}^{\infty}\mathrm{exp}\left[-2B\left(z^2 - (x_i + x_j)z \right)-B(x_i^2 + x_j^2)\right]\ dz\\
&=&A^2\ \int_{-\infty}^{\infty}\mathrm{exp}\left[-2B\left(z - \frac{1}{2}(x_i + x_j) \right)^2  +\frac{B}{2}(x_i + x_j)^2-B(x_i^2 + x_j^2)\right]\ dz\\
&=&A^2\ \int_{-\infty}^{\infty}\mathrm{exp}\left[-2B\left(z - \frac{1}{2}(x_i + x_j) \right)^2  -\frac{B}{2}(x_i - x_j)^2\right]\ dz\\
&=&A^2\  \int_{-\infty}^{\infty}\mathrm{exp}\left[-2B\left(z - \frac{1}{2}(x_i + x_j) \right)^2  \right]\mathrm{exp}\left[-\frac{B}{2}(x_i-x_j)^2\right]\ dz\\
&=&A^2\ \mathrm{exp}\left[-\frac{B}{2}(x_i-x_j)^2\right] \int_{-\infty}^{\infty}\mathrm{exp}\left[-2B\left(z - \frac{1}{2}(x_i + x_j) \right)^2  \right]\ dz\\
&=&A^2\sqrt{\frac{\pi}{2B}}\ \mathrm{exp}\left[-\frac{B}{2}(x_i-x_j)^2\right]\\
&=&α\ \mathrm{exp}\left(β(x_i-x_j)^2\right)\\

\end{eqnarray}