はじめに

状態空間モデルは時系列分析の１手法。時系列での変動を複数の成分に分解してモデリングできるため、解釈性が高い。近年、状態空間モデルについて分かりやすく解説している書籍が複数出版されている。

この記事で解説しないこと

状態空間モデル、カルマンフィルターとは？
RのKFAS、dlmでの実装
statsmodelsの基本的な使い方

下記の参考書籍や解説記事を参照。

この記事で解説すること

statsmodelsのMLEModelを使って、自由に状態空間モデルを実装する方法
実装したモデルのサンプルデータへの適用

状態空間モデルの参考文献

時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装
紹介する３冊の中で一番数式が少なく、平易に書かれている。とりあえず状態空間モデルのイメージをつかんで、Rで実装できるようになれば良い、という人におすすめ。RのKFASによる実装が中心だが、dlmにも触れている。
基礎からわかる時系列分析 ―Rで実践するカルマンフィルタ・MCMC・粒子フィルター
ボリュームだっぷりの１冊。他の本には記載のないウィーナーフィルタなどにも触れている。コードがたっぷりで応用的なモデルの実装も学べる。Rのdlmライブラリを使用。
カルマンフィルタ ―Rを使った時系列予測と状態空間モデル―
数式ベースでの解説が一番丁寧な一冊。タイトルの通り、カルマンフィルタの理解には一番おすすめ。粒子フィルタの解説もある。KFASのサンプルコードも載っている。

いずれも数式での解説からRのコードまで載っており、かなり参考になった。
一方で、最近はPythonでの実装が求められることもあるのではないか。

Pythonで状態空間モデルというとstatsmodelsというライブラリが使われるが、いかんせん公式リファレンスの説明が少なすぎて、いまいち使い方が分かりづらい。
statsmodelsによる状態空間モデルの基本については、こちらの記事に解説がある。

本記事ではstatsmodelsのもう少し発展的な使い方を解説する。

statsmodelsによる一般ガウス状態空間モデル

一般ガウス状態空間モデルは下式で表される。
<更新予定>

一番基本的な状態空間モデルであるローカルレベルモデルは全ての係数行列が単位行列のモデル。
係数行列を適切に指定することで、トレンド成分モデル、周期成分モデルなど様々なモデルを表現することができる。
RのKFASやPythonのstatsmodelsでは、係数行列を直接指定してモデルを構築することができる。

ただし、基本的なモデルはもっと簡単に実装する方法が用意されている。

UnobservedComponentsクラス

statsmodelsでトレンドや周期成分、回帰成分などを組み込んだモデルを実装する場合、基本的にはUnobservedComponentsというクラスを使う。

ただし、UnobservedComponentsでは、時変の係数を用いた回帰成分モデルが設定できない、複数の周期成分を組み込めない、既知の値で状態を初期化できないなど、モデリングの自由度は低い。

例えば、カルマンフィルタの利点は逐次的な予測ができることであり、実用上はオンライン予測を行うことも多いはず。その場合、まず一定期間のデータでカルマンフィルタを実行後、新たに得られたデータで再度フィルタリングを行うことになる。その際、前回のカルマンフィルタの最終時点の状態予測値に基づいて、次のフィルタリングに用いる状態の初期値や予測誤差分散を決定することになる。

ところが、UnobservedComponentsでは近似的な散漫初期化（簡単に言うと、初期状態についてまったく手がかりがないと考えること）がデフォルトになっており、既知の値で初期化することができない。
こうしたケースでは、MLEModelを使う必要がある。

MLEModelクラス

自分で好きなモデルを設定する場合は、公式リファレンスに説明がある通り、MLEModelというクラスを使えば良い。
ローカル線系トレンドモデルの実装方法について、公式サイトに解説がある。ただし、このモデルの場合はUnobservedComponentsで実装できる。

ここでは、UnobservedComponentsでは実現できない下記２点を満たすモデルの実装を紹介する。

回帰係数が時変の回帰成分モデル
初期化の方法が選択可能

CustomizeMLEmodel.py

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

"""
Regression Model
"""
class StateSpaceRegression(sm.tsa.statespace.MLEModel):
    def __init__(self, endog, exog, initialization, initial_state=None, initial_state_cov=None):
        # Model order
        # k_state:  状態の次元
        # k_posdef: 過程誤差分散行列の次元
        k_states = k_posdef = 2

        # Initialize the statespace
        super(StateSpaceRegression, self).__init__(
            endog, exog=exog, k_states=k_states, k_posdef=k_posdef,
            initialization=initialization, initial_state=initial_state, initial_state_cov=initial_state_cov,
            loglikelihood_burn=k_states
        )

        # Initialize the matrices
        # 時間変化するdesign matirxで説明変数を表す。
        n_obs = len(exog)
        self.ssm['design'] = np.vstack((np.repeat(1, n_obs), exog))[np.newaxis, :, :]

        self.ssm['transition'] = self.ssm['selection'] = np.eye(k_states)

        # updateでself.ssmにstate_covの値をセットするために用いる
        self._state_cov_idx = ('state_cov',) + np.diag_indices(k_posdef)

    @property
    def param_names(self):
        return ['sigma2.measurement', 'sigma2.intercept', 'sigma2.coefficient']

    @property
    #  パラメータの最尤推定の際の初期値
    def start_params(self):
        return [np.std(self.endog)]*3

    def transform_params(self, unconstrained):
        return unconstrained**2

    def untransform_params(self, constrained):
        return constrained**0.5

    def update(self, params, *args, **kwargs):
        params = super(StateSpaceRegression, self).update(params, *args, **kwargs)

        # Observation covariance
        self.ssm['obs_cov',0,0] = params[0]

        # State covariance
        self.ssm[self._state_cov_idx] = params[1:]

ポイントは下記の通り。

k_state, k_posdef: 状態ベクトルと過程誤差分散行列の次元。目的変数（観測値）の次元はデータから推測されるので与える必要がない。
update: fitメソッドでパラメータを最尤推定する際に用いられる。パラメータを受け取り、適切な状態空間行列を設定する。
statespace matrices: デフォルトでは全ての行列がゼロ行列となっている。単位行列でないことに注意。時間変化する場合はupdateメソッドで設定する必要がある。self.ssmに格納されている。
start params: 分散パラメータの最尤推定の際の初期値
initialization: 状態ベクトルの初期分布の平均値と分散を設定する必要がある。初期分布が既知の場合はinitialize_known、不明の場合はinitialize_approximate_diffuse(近似的な散漫初期化)を用いる。
transform: デフォルトでは制約なしでパラメータ推定が行われるが、transform_paramsを設定することで、正値をとる分散のように制約付きのパラメータに変換することができる。
param_names: 推定するパラメータに名前をつけられる。

実データへの適用

上記3冊目の参考文献のサポートサイトから入手できるサンプルデータを使って実験した結果を載せる。

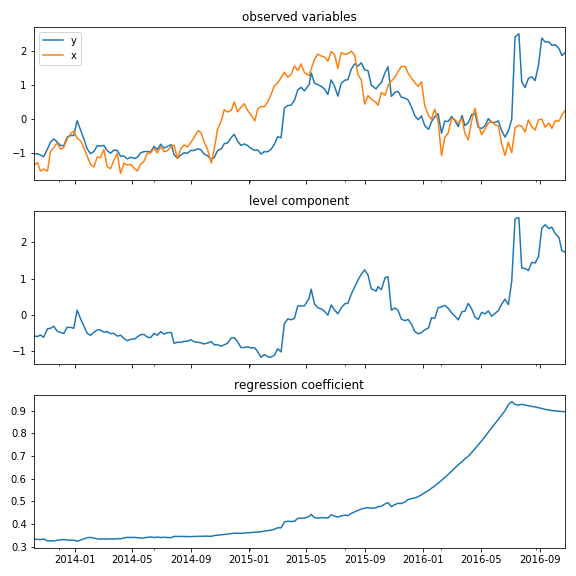
最初のプロットは実測値。$x$（オレンジ）を説明変数とした時変係数の回帰成分モデルで$y$（ブルー）を予測している。
２番目のプロットは水準成分、３番目のプロットは回帰係数を表している。
このデータの場合、期間後半になるほど回帰係数が増加傾向にあることが分かる。

コードはこちら。

nintendo = pd.read_csv('data/NINTENDO.csv', index_col=0, parse_dates=[0])
nikkei = pd.read_csv('data/NIKKEI225.csv', index_col=0, parse_dates=[0])

def scaler(s):
    return (s - s.mean()) / s.std()

endog, exog = scaler(nintendo.Close), scaler(nikkei.Close)

# 時変回帰係数のモデル
mod_reg = StateSpaceRegression(endog, exog, initialization='approximate_diffuse')

res_mod_reg = mod_reg.fit()
res_mod_reg.summary()

# 状態の一期先予測
mu_pred, beta_pred  = res_mod_reg.predicted_state
# 平滑化状態
mu_smoothed, beta_smoothed = res_mod_reg.smoothed_state


fig, axes = plt.subplots(3, 1, figsize=(8, 8), sharex=True)
endog.plot(ax=axes[0], label='y')
exog.plot(ax=axes[0], label='x')
axes[0].set_title('observed variables')
axes[0].legend()

axes[1].plot(endog.index, mu_smoothed)
axes[1].set_title('level component')

axes[2].plot(endog.index, beta_smoothed)
axes[2].set_title('regression coefficient')

おまけ： TensorFlow Probabilityという選択肢

statsmodelsを使う場合は、最尤法＋カルマンフィルタでパラメータを点推定することになるが、ベイジアンモデリングにできると、自在なモデルを構築、推定可能で、予測の確信度も自然に定量化できるという利点がある。

ベイズ状態空間モデルの実装にはStanを使うのがスタンダードなようだが、どうしてもコーディングの労力がかかってしまう。また、pystanもあるものの、Rで使うことが多い気もする。

Pythonでベイズ状態空間モデルを実装するとき、新たな選択肢としてTensorFlow Probability（TFP）のstsモジュールがある。公式記事参照。

ただ、2019.12現在、TFPは絶賛開発中ということもあり、まだ安定して使える感じではない。今後に期待！

Pythonで一般ガウス状態空間モデル