ベイジアンモデリングをしていると、多変量正規分布の分散共分散行列の事前分布を設定したいというシチュエーションがある。
普通の(単変量)正規分布の標準偏差の事前分布を設定する場合は、パラメータの条件としては正の値を取ることだけなので逆ガンマ分布、半コーシー分布、半正規分布などの正の値しか取らない確率分布を適当に設定すれば良い。
一方、共分散行列の事前分布を設定する場合、半正定値行列を返すような確率分布ではならない。半正定値行列とは固有値が全て0以上の行列のことである。共分散行列がなぜ必ず半正定値行列なのかについての証明はこちらのページが参考になる。
分散共分散行列の事前分布としては逆ウィシャート分布が挙げられるが、PyMC3のドキュメントいわく、moden Bayesian computational methodには適していないらしい。その代わり、相関係数の事前分布である「LKJ分布」を用いることが推奨されている。
LKJ分布の確率密度関数は下記の通り。LKJというのは論文の著者3名のイニシャルらしい。
$$f(\Sigma;\eta)=Z(\eta)\dot \rm{det} (\Sigma)^{\eta-1}$$
パラメータ$\eta$は正値であり、PyMC3, Stanではshape parameter, TensoFlow Probability ではconcentration parameterと呼ばれている。また、$Z(\eta)$は正規化定数($f$の全範囲に渡る積分が1になるよう調整するための定数)である。
$\eta$=1の場合はUniform distributionとなる。また、$\eta$が大きいほど変数間の相関が小さくなり、$\eta$が小さいほど相関が大きくなる。
...と言われてもいまいちイメージが湧かない。そこで相関行列を可視化することを考える。
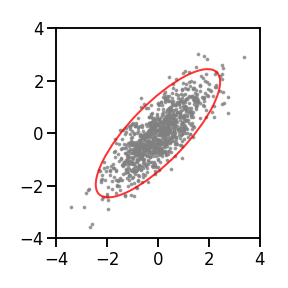
例えば、
$$\mu=(0,0),\quad \Sigma = \begin{pmatrix}1.0 & 0.8 \\ 0.8 & 1.0 \end{pmatrix}$$
とした二変量正規分布からサンプルを取得し、グレーの点で表示すると下図のようになる。こちらは相関係数0.8と、2変数の相関の高い例である。このグレーの点の分布の形状を表すために、95%信頼区間を赤線で表している。
このように、LKJ分布から得られたサンプル$\Sigma$を用いた二変量正規分布について、赤い楕円をプロットしていけば、相関行列を可視化することができる。
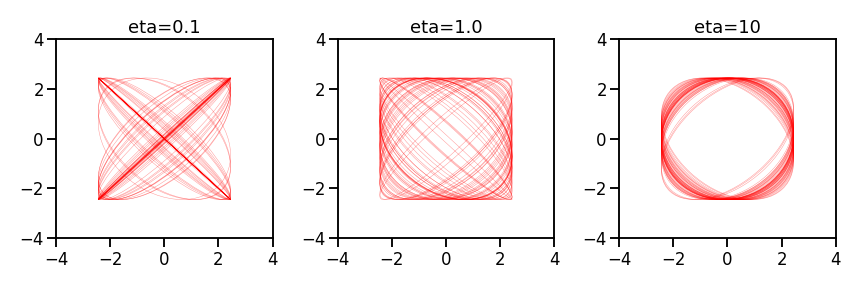
以下に、平均(0, 0)、共分散行列をLKJ分布からのサンプルとした二変量正規分布の95%信頼区間を表示する。$\eta=0.1, 1.0, 10$のLKJ分布から相関行列をそれぞれ50個サンプリングし、重ね書きしている。
$\eta=0.1$の場合は斜めを向いた楕円が多く、相関係数の絶対値が大きい行列が得られやすいことが分かる。$\eta=1$の場合はUniform distributionなので、相関が高いケースから低いケースまで均等にサンプルが得られている。また、$\eta=10$の場合は真円に近く、相関係数が低い相関行列が得られやすいことが分かる。
なお、通常はLKJ分布から相関行列を直接サンプリングすることはなく、コレスキー分解した行列Lをサンプリングする。コレスキー分解では下三角行列$L$とその転置行列の積で共分散行列を表す。
多変量正規分布の計算では共分散行列$\Sigma$の逆行列が必要になるが、その際、コレスキー分解した行列$L$を用いた方が計算が早く数値的にも安定するらしい。
Stanのドキュメントにも相関行列のサンプリングは「実行速度が遅く、メモリ消費量が増え、数値上のエラーが発生する危険が高いコードを書きたいときに使う」との記載がある。笑
PyMC3, Stan, TFPでLKJ分布からコレスキー分解された相関行列(共分散行列)を得る方法をまとめてみた。
| フレームワーク | 名称 | 備考 |
|---|---|---|
| PyMC3 | pymc3.distributions.multivariate.LKJCholeskyCov | sd_dist引数に標準偏差の確率分布を与えることで、共分散行列のサンプリングが可能。 |
| Stan | lkj_corr_cholesky | |
| TFP | tfp.distributions.LKJ | コレスキー分解した行列を得るためには、input_output_cholesky=Trueとする必要がある。 |
また、共分散行列の話がいつの間にか相関行列に変わっているが、例えば二変量の場合、両者は下記のように変換できる。ここで、$\sigma_1, \sigma_2$は各変数の標準偏差、$\sigma_{12}$は共分散、$\rho_{12}$は相関係数である。
$$\begin{pmatrix} \sigma_1^2 & \sigma_{12} \\ \sigma_{12} & \sigma_2^2 \end{pmatrix}=\begin{pmatrix}\sigma_1 & 0 \\ 0 & \sigma_2 \end{pmatrix} \begin{pmatrix}1.0 & \rho_{12} \\ \rho_{12} & 1.0 \end{pmatrix} \begin{pmatrix}\sigma_1 & 0 \\ 0 & \sigma_2 \end{pmatrix}$$
つまり、相関行列に加えて、標準偏差もサンプリングしておくことで、任意の共分散行列が表せることになる。PyMC3のLKJCholeskyCovはこの操作をまとめて行ってくれるので便利そう。
可視化に用いたコードはこちら。TensorFlow Probabilityを使用している。
from matplotlib.patches import Ellipse
from matplotlib import pyplot as plt
import seaborn as sns
import numpy as np
from scipy import stats
import tensorflow as tf
import tensorflow_probability as tfp
sns.set_context('talk')
# draw 95% confidence interval of multivariate normal distribution
def draw_ellipse(cov, ax):
var, U = np.linalg.eig(cov)
angle = 180. / np.pi * np.arctan(U[0, 0]/ U[1, 0])
e = Ellipse(np.zeros(2), 2 * np.sqrt(5.991 * var[0]), 2 * np.sqrt(5.991 * var[1]),
angle=angle, facecolor='none', edgecolor='r', linewidth=0.5, alpha=0.4)
ax.add_artist(e)
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
# visualize samples from LKJ prior
def visualize_LKJ(eta, n_sample, ax):
dist = tfp.distributions.LKJ(dimension=2, concentration=eta)
sample = dist.sample(sample_shape=n_sample, seed=42)
with tf.Session() as sess:
cov_samples = sess.run(sample)
for cov in cov_samples:
draw_ellipse(cov, ax)
ax.set_title(f'eta={eta}')
eta_list = [0.1, 1.0, 10]
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
for i, eta in enumerate(eta_list):
visualize_LKJ(eta, 50, axes[i])
plt.tight_layout()
# plt.savefig('LKJ_sample.png')