概要
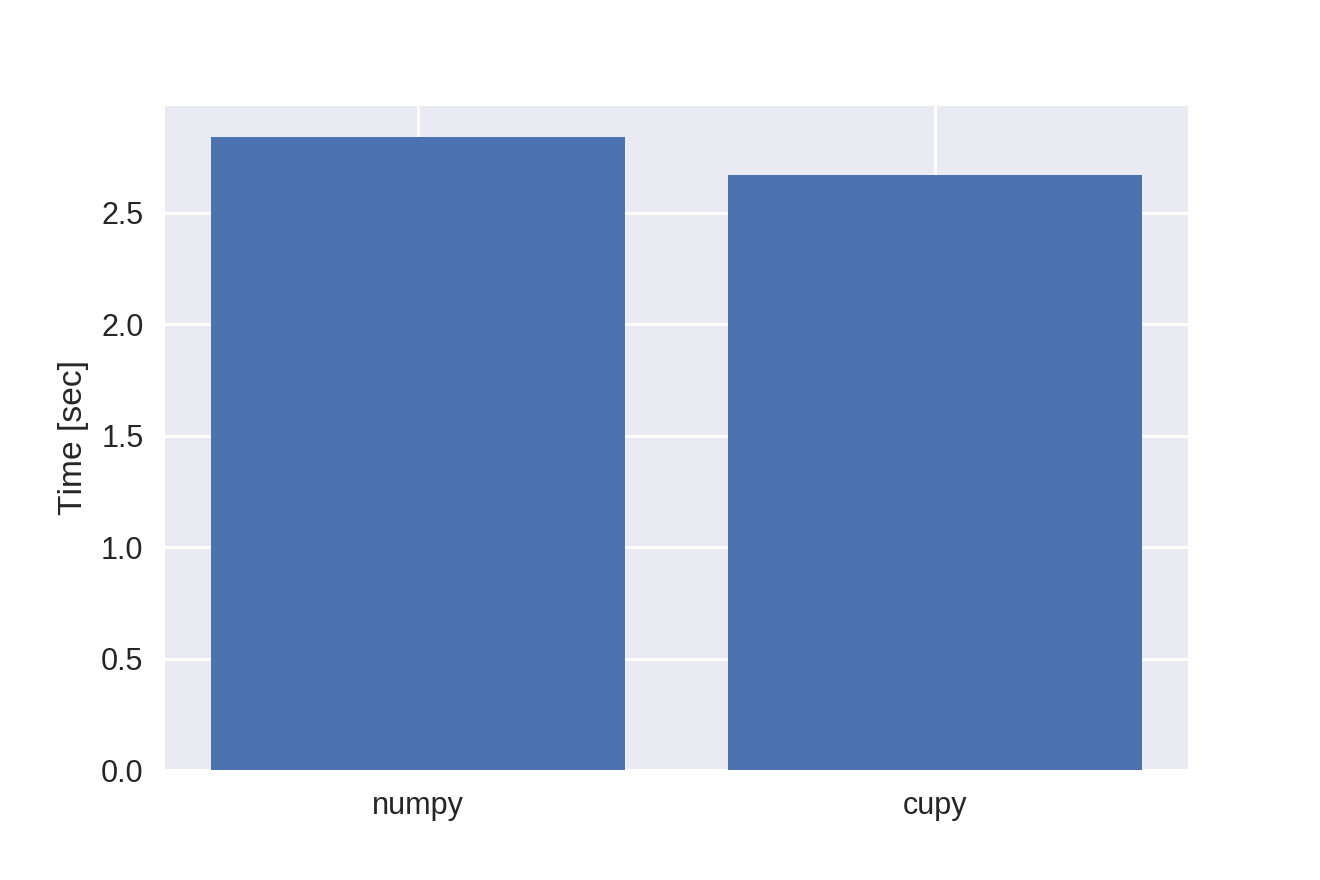
主双対近接分離法による全変動最小化に基づく画像復元をnumpy、cupyで実装し、処理速度を比較しました。
Google ColaboratoryのランタイムのGPUで計測しました。
計算時間が94%に減少しました。
残念ながら、あまり速くなりませんでした…
CuPyのインストール
!apt -y install libcusparse8.0 libnvrtc8.0 libnvtoolsext1
!ln -snf /usr/lib/x86_64-linux-gnu/libnvrtc-builtins.so.8.0 /usr/lib/x86_64-linux-gnu/libnvrtc-builtins.so
!pip install https://github.com/kmaehashi/chainer-colab/releases/download/2018-02-06/cupy_cuda80-4.0.0b3-cp36-cp36m-linux_x86_64.whl
!pip install 'chainer==4.0.0b3'
インポート、パラメータ
import numpy as np
import cupy as cp
import matplotlib.pyplot as plt
%matplotlib inline
lambda_ = 500
gamma1 = 0.003
gamma2 = 1 / (8 * gamma1)
maxIter = 1000
stopcri = 0.01
cmap = 'gray'
# numpy or cupy
# xp = np
xp = cp
xp = np/cpでnumpyとcupyを切り替えます。
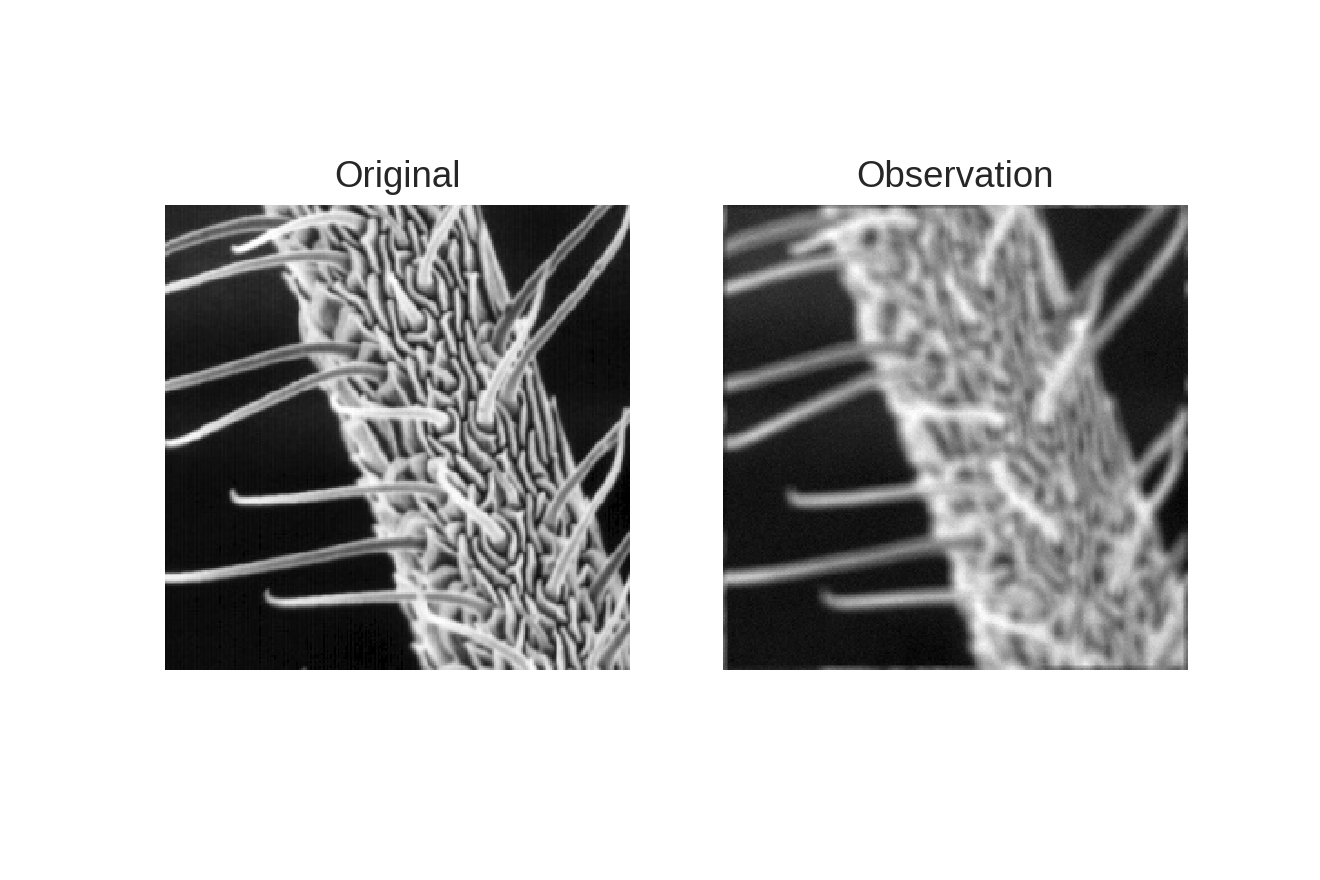
観測データの生成
from skimage.io import imread
u_org = imread("Culicoidae256.png", as_grey=True) / 255.
u_org = xp.array(u_org)
rows, cols = u_org.shape
N = rows * cols
# blur operator
psfsize = 7
psf = xp.ones((psfsize, psfsize))
psf /= xp.sum(psf)
blu = xp.zeros(u_org.shape)
blu[:psf.shape[0], :psf.shape[1]] = psf
blu = xp.roll(blu, -(psfsize//2), 0)
blu = xp.roll(blu, -(psfsize//2), 1)
bluf = xp.fft.fft2(blu)
bluft = xp.conj(bluf)
Phi = lambda z: xp.fft.ifft2(xp.fft.fft2(z) * bluf).real
Phit = lambda z: xp.fft.ifft2(xp.fft.fft2(z) * bluft).real
sigma = 2.5 / 255 # noise standard deviation
xp.random.seed(42)
v = Phi(u_org) + sigma * xp.random.randn(rows, cols)
fig, ax = plt.subplots(1, 2)
ax = ax.flatten()
if xp == cp:
ax[0].imshow(cp.asnumpy(u_org), cmap=cmap)
ax[1].imshow(cp.asnumpy(v), cmap=cmap)
else:
ax[0].imshow(u_org, cmap=cmap)
ax[1].imshow(v, cmap=cmap)
ax[0].set_title('Original')
ax[1].set_title('Observation')
for a in ax:
a.axis('off')
plt.savefig("data.png", dpi=220)
Primal Dual Splitting
from skimage.measure import compare_psnr
import time
# difference operator
D = lambda z: xp.dstack((xp.roll(z, -1, 0) - z, xp.roll(z, -1, 1) - z))
Dt = lambda z: xp.r_[-z[:1, :, 0] + z[-1:, :, 0], -z[1:, :, 0] + z[:-1, :, 0]] + xp.c_[-z[:, :1, 1] + z[:, -1:, 1], -z[:, 1:, 1] + z[:, :-1, 1]]
# variables
u = v
z = D(v)
start = time.time()
for i in range(maxIter):
upre = u.copy()
# update u
nablaF = lambda_ * Phit(Phi(u) - v)
u = u - gamma1 * (nablaF + Dt(z))
u[u > 1] = 1
u[u < 0] = 0
# update z
z = z + gamma2 * D(2 * u - upre)
temp = z / gamma2
onemat = xp.ones((rows, cols))
thresh = 1 / xp.sqrt(xp.sum(temp ** 2, 2)) / gamma2
thresh[thresh > 1] = 1
coef = onemat - thresh
temp = xp.dstack((coef, coef)) * temp
z = z - gamma2 * temp
# stopping condition
error = u - upre
error = xp.linalg.norm(error)
# print(compare_psnr(u_org, u))
if error < stopcri:
break
print(time.time() - start)
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
ax = ax.flatten()
if xp == cp:
ax[0].imshow(cp.asnumpy(u_org), cmap=cmap)
ax[1].imshow(cp.asnumpy(v), cmap=cmap)
ax[2].imshow(cp.asnumpy(u), cmap=cmap)
else:
ax[0].imshow(u_org, cmap=cmap)
ax[1].imshow(v, cmap=cmap)
ax[2].imshow(u, cmap=cmap)
ax[0].set_title('Original\nPSNR [dB]')
if xp == cp:
ax[1].set_title('Observation\n{:.2f}'.format(compare_psnr(cp.asnumpy(u_org), cp.asnumpy(v))))
ax[2].set_title('Restored\n{:.2f}'.format(compare_psnr(cp.asnumpy(u_org), cp.asnumpy(u))))
else:
ax[1].set_title('Observation\n{:.2f}'.format(compare_psnr(u_org, v)))
ax[2].set_title('Restored\n{:.2f}'.format(compare_psnr(u_org, u)))
for a in ax:
a.axis('off')
plt.savefig("result.png", dpi=220)
考察
- 複数枚の画像を同時に処理すれば加速できるかも
- 凸最適化、圧縮センシングを手軽にGPUで走らせられるのはよい
- ラドン変換がcupyに入れば、画像再構成をGPUでできるんだけどな〜(^_-)