生物学データの次元削減・可視化手法PHATEを使ってみる

PHATE（Moon, K.R., van Dijk, D., Wang, Z. et al. Nature Biotechnology 37, 1482–1492 (2019))を使ってみる。

生物学の論文で使われる次元削減の手法は山のようにあるけど、どの手法も一長一短。代表的なものとしてたとえば以下のような手法がよく使われる。
1. PCA: 主成分分析。分散最大の軸を取り出す。他の手法にはない色んな利点があるけど、特に可視化に使う場合には、非線形な特徴が捉えられない、分布の大域的特徴を良く反映するぶん局所的な構造がノイズとしてつぶれがち、などの欠点がある。
2. t-SNE（およびUMAP）: それぞれの点についてlocal neighborhoodとの距離関係が保存されるように低次元の配置を探索する。なのでデータ分布の局所的構造がよく保存された可視化となる。データが複数のクラスタから構成されている場合などはそれらのクラスタを良く反映した可視化となるが、連続的な「軌道」などは適当に分割されてしまいがち。また長距離の関係性をほとんど見ないので、複数のクラスタ間の相対的な距離関係は乱数によってもコロコロ変わる。
3. MDS: 多次元尺度構成法。データ点間の全対全の距離関係を保存するように配置。データの「構造」を直接は見ないので、ノイズに弱い（ノイズと、クラスタや軌道といった特徴的な構造を区別しない）
4. Diffusion map: データ点間の距離から遷移確率行列を構成して、diffusion process（データのグラフ構造上のランダムウォーク）を作用させる。tステップ後の分布は遷移確率行列のt乗で得られる。その分布の違いをユークリッド距離として反映するような低次元座標を得たいのだけど、それが遷移確率行列のt乗の固有ベクトルとして得られる、という手法。ノイズに強い、ステップ数tによって局所的な特徴から大域的構造まで対応できる、「軌道」のような構造を見つけやすい、など色んな利点があるけど、異なる軌道を異なる次元に圧縮しがち。つまり二次元、三次元などの低次元での可視化には向かない。
5. Monocle2などのTrajectory inference: 木構造を推定する手法なので、その前提が成り立つのかどうか、事前にはよくわからない。また推定も不安定。

などなど。こういった欠点を解消しようと開発されたのが、PHATE (Potential of Heat diffusion for Affinity-based Transition Embedding)という手法。

また、より一般的なテンソルの埋め込みとして、PHATEを拡張したM-PHATEも開発されている。こっちは同一の集団の時間発展を含むようなデータ（ニューラルネットワークのエポックごとの重みの情報など）を低次元可視化する手法。

インストールは簡単で、pip install phateとすればOK.

Rバージョン、MatlabバージョンなどはPHATEのレポジトリ参照。

木構造データの可視化

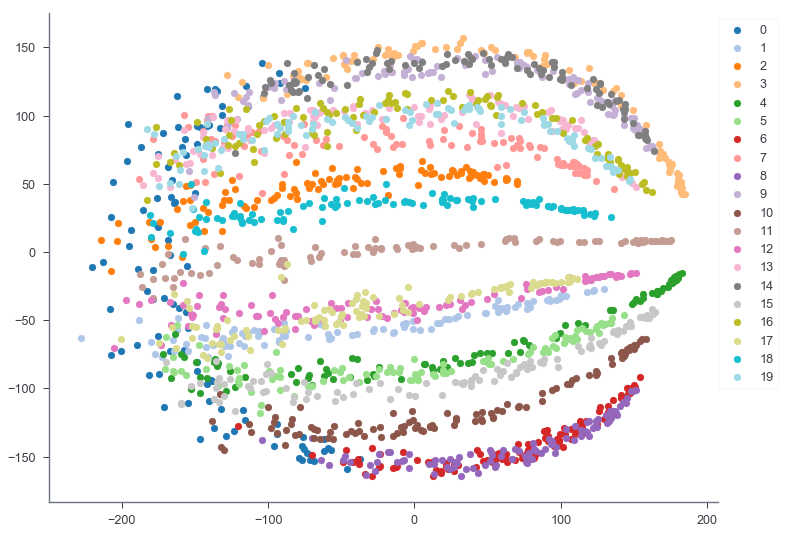
PHATEが提供している100次元の木構造データ（+ノイズ）で実験してみる。20本の「枝」から構成され、データ点の数は合計2,000。構造としては、一本目の枝の様々なところからランダムに、残り19本の枝が生えているデータ。それぞれの枝は100次元空間で様々な方向を向いている。

import phate

tree_data, tree_clusters = phate.tree.gen_dla(seed=108)

使い方はscikit-learnのモデルと同じ。まずパラメータ設定してモデルのインスタンスを作って、fit_transformでデータを変換する。

主要なパラメータはknn, decay, tの三つ。tはデータから自動決定もできる。詳細は後述。

phate_operator = phate.PHATE(knn=15, decay=40, t=100)

tree_phated = phate_operator.fit_transform(tree_data)

    Calculating PHATE...
      Running PHATE on 2000 cells and 100 genes.
      Calculating graph and diffusion operator...
        Calculating KNN search...
        Calculated KNN search in 0.50 seconds.
        Calculating affinities...
        Calculated affinities in 0.05 seconds.
      Calculated graph and diffusion operator in 0.56 seconds.
      Calculating diffusion potential...
      Calculated diffusion potential in 0.41 seconds.
      Calculating metric MDS...
      Calculated metric MDS in 10.43 seconds.
    Calculated PHATE in 11.41 seconds.

二次元に圧縮した。結果をプロットしてみる。

import matplotlib.pyplot as plt
import seaborn as sns

def plot_2d(coords, clusters, ax):
    for c, color in zip(sorted(list(set(clusters))), plt.cm.tab20.colors):
        samples = clusters == c
        ax.scatter(coords[samples, 0], coords[samples, 1], \
                   label=c, color=color)
    ax.legend(loc='upper right', bbox_to_anchor=(1.1, 1))
    sns.despine()

fig, ax = plt.subplots(figsize=(12, 9))
plot_2d(tree_phated, tree_clusters, ax=ax)
plt.show()

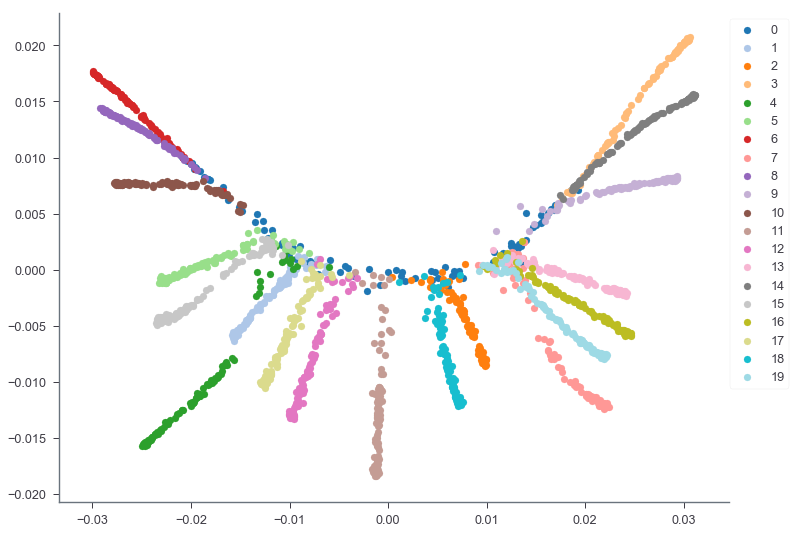
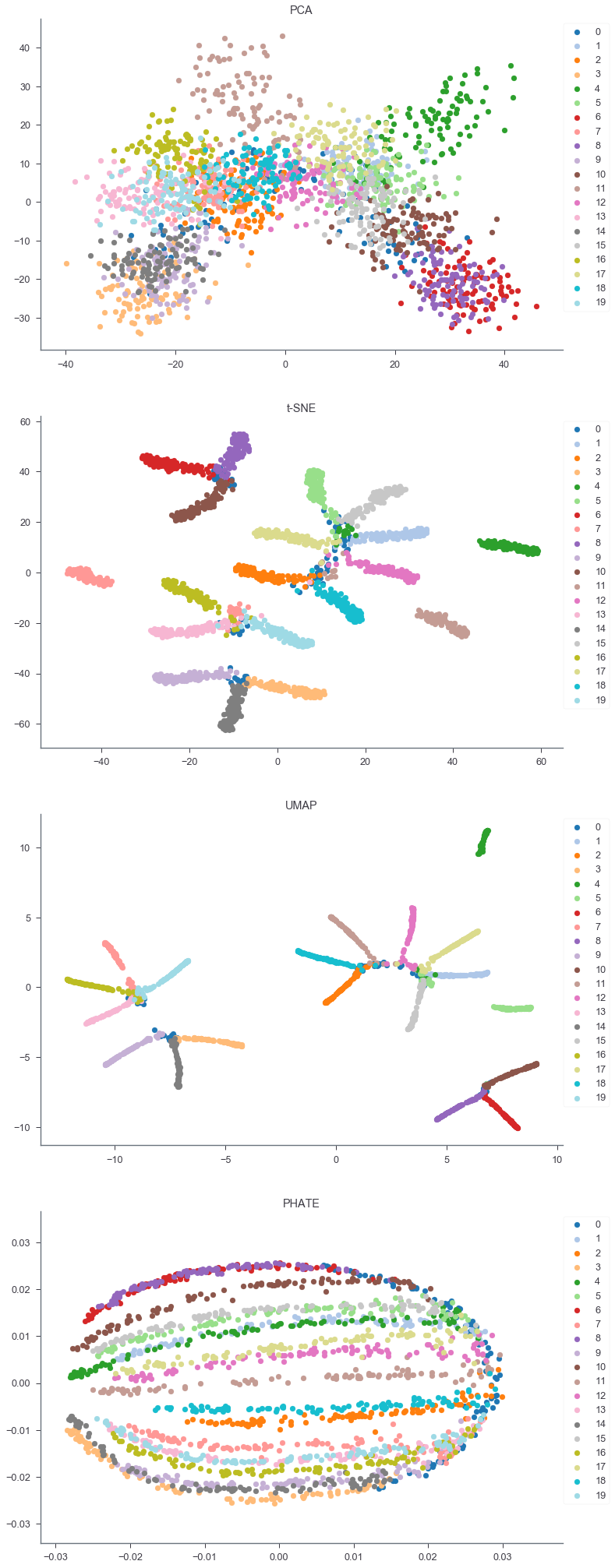
このように、データの構造を保ってちゃんとそれぞれの枝を分離して可視化できている。同じデータでPCA, t-SNE, UMAP, PHATEの可視化を比較してみる。

from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
from umap import UMAP

def compare_vis(data, clusters, pca_init_dim=100):
    print('Running PCA...')
    pca_op = PCA(n_components=2)
    data_pca = pca_op.fit_transform(data)
    print('Running t-SNE...')
    pca_init_op = PCA(n_components=pca_init_dim)
    tsne_op = TSNE(n_components=2)
    data_tsne = tsne_op.fit_transform(pca_init_op.fit_transform(data))
    print('Running UMAP...')
    pca_init_op = PCA(n_components=pca_init_dim)
    umap_op = UMAP(n_components=2)
    data_umap = umap_op.fit_transform(pca_init_op.fit_transform(data))
    print('Running PHATE...')
    phate_op = phate.PHATE(n_components=2)
    data_phated = phate_op.fit_transform(data)
    fig, axes = plt.subplots(figsize=(12, 36), nrows=4)
    plot_2d(data_pca, clusters, ax=axes[0])
    plot_2d(data_tsne, clusters, ax=axes[1])
    plot_2d(data_umap, clusters, ax=axes[2])
    plot_2d(data_phated, clusters, ax=axes[3])
    axes[0].set_title('PCA'); axes[1].set_title('t-SNE')
    axes[2].set_title('UMAP'); axes[3].set_title('PHATE')
    plt.show()    

compare_vis(tree_data, tree_clusters)

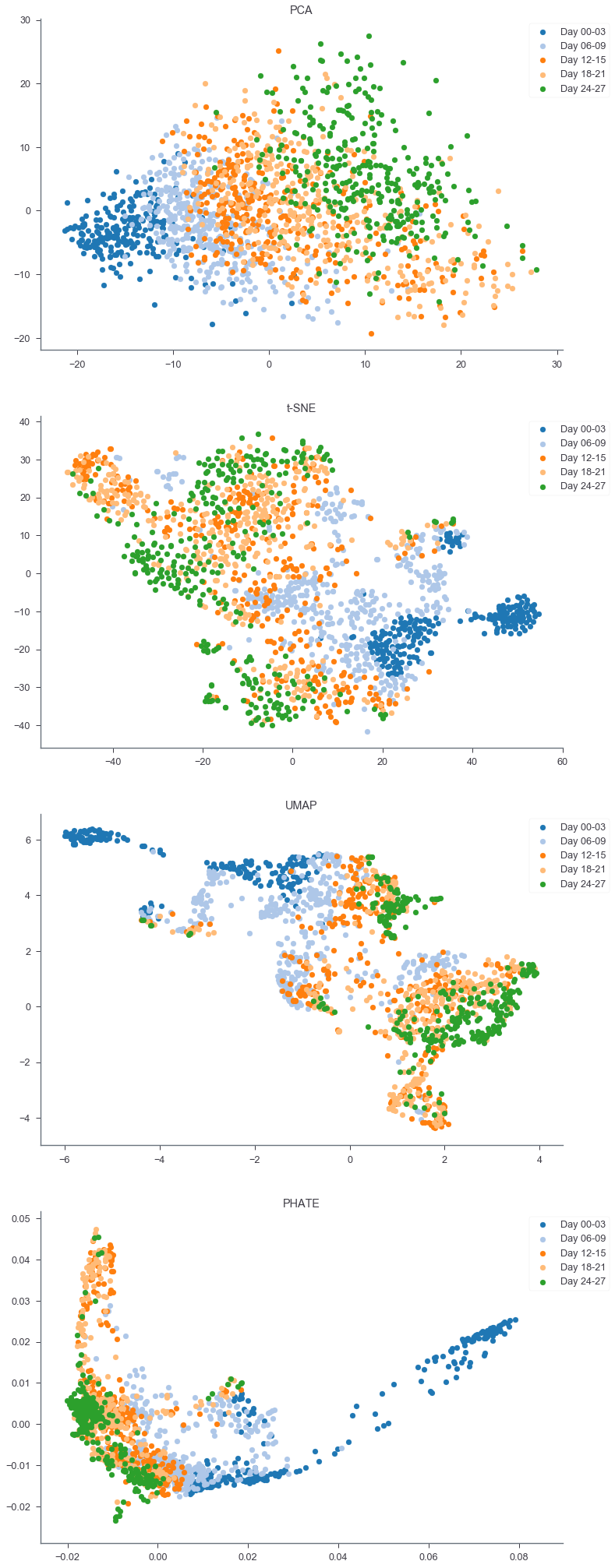
PCAでは（ノイズの影響が大きいため）木構造がよくわからず、t-SNEやUMAPでは適当にクラスタを分割してしまっている。

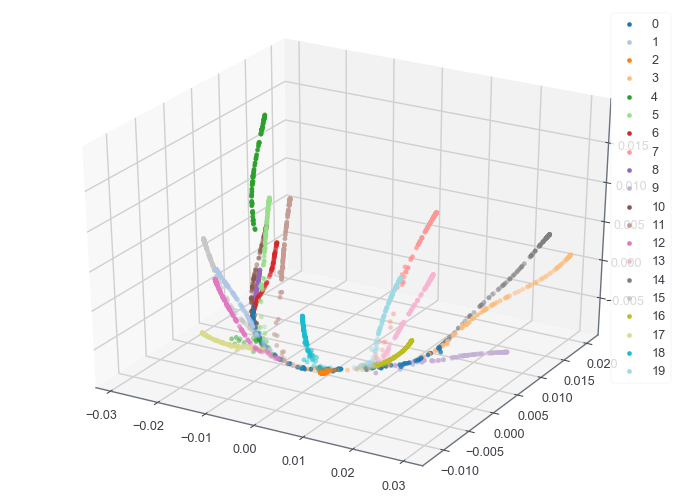
３次元への埋め込みも見てみる。後述するがPHATEのアルゴリズムにおいて、最終的に埋め込む次元は最後のMDS計算にしか関わらないので、全体を再計算する必要はなく、パラメータ（n_components）をアップデートしてtransformすれば最終ステップだけ実行してくれる。

%matplotlib notebook
from mpl_toolkits.mplot3d import axes3d

def plot_3d(coords, clusters, fig):
    ax = fig.gca(projection='3d')
    for c, color in zip(sorted(list(set(clusters))), plt.cm.tab20.colors):
        samples = clusters == c
        ax.scatter(coords[samples, 0], coords[samples, 1], coords[samples, 2], \
                   label=c, color=color)
    ax.legend()

phate_operator.set_params(n_components=3)
tree_phated = phate_operator.transform()

fig = plt.figure(figsize=(12, 9))
plot_3d(tree_phated, tree_clusters, fig)

scRNA-seqデータの可視化

論文でデモンストレーションに使用されている胚様体のscRNA-seqデータで試してみる。

ちょっとデータが大きすぎるのと、ダウンサンプリングしたときの結果の安定性の評価も兼ねて、全体の10%だけランダムに細胞をサンプリングして、いくつか普通の前処理を実行した結果を事前に作った。

scRNA-seqのデータ前処理や、PCA, t-SNE, UMAPなどのアルゴリズムの詳細については講習会の動画など参照。

import numpy as np
import pandas as pd
import scipy

cells = np.genfromtxt('./data/cell_names.tsv', dtype='str', delimiter='\t')
genes = np.genfromtxt('./data/gene_names.tsv', dtype='str', delimiter='\t')
arr = scipy.io.mmread('./data/matrix.mtx')

EBData = pd.DataFrame(arr.todense(), index=cells, columns=genes)
EBData.head()

1,679細胞、12,993遺伝子の遺伝子発現量テーブル。

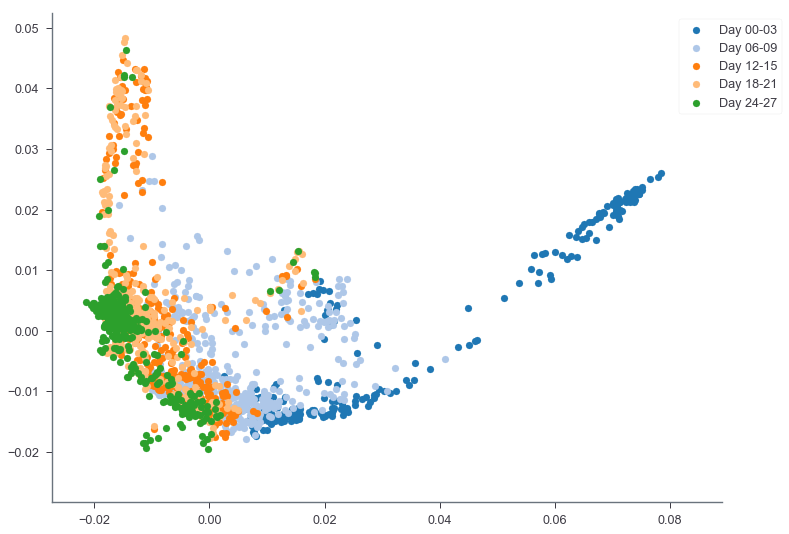
各細胞は以下のようにラベリングされている。27日目まで3日ごとにとられているため、分化の時系列が観測できるはず。

sample_labels = EBData.index.map(lambda x:x.split('_')[1]).values
print(sample_labels)

    array(['Day 00-03', 'Day 00-03', 'Day 00-03', ..., 'Day 24-27',
           'Day 24-27', 'Day 24-27'], dtype=object)

phate_op = phate.PHATE()
EBData_phated = phate_op.fit_transform(EBData)

%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 9))
plot_2d(EBData_phated, sample_labels, ax=ax)
plt.show()

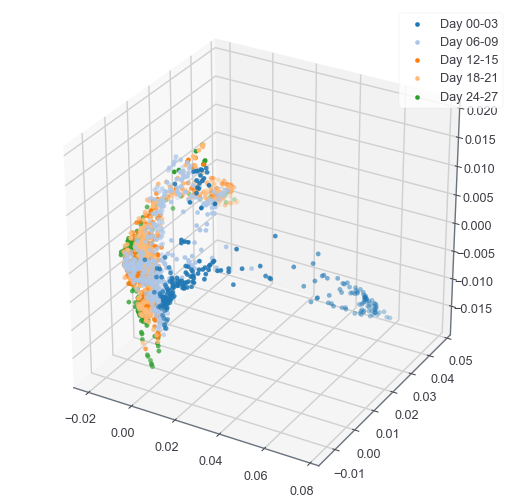
PHATEによる次元削減＋可視化では分化のプロセスがよくわかる。とくに、18日目から27日目にかけての多様性の広がりとか。こんな感じで、軌道があるときはちゃんと軌道として、クラスタがあるときはちゃんとクラスタらしく、さらにクラスタの広がりについても相互に比較可能な可視化を実行してくれるのがPHATEのいいところ。また、全データの10%しか使っていないにも関わらず、数万細胞を使って次元圧縮した論文の図（論文のFig.1c）とほとんど同じ描画をしてくれていることから、サンプルサイズにもある程度ロバストであることがわかる。

３次元もやってみる。

phate_op.set_params(n_components=3)
EBData_phated = phate_op.transform()
fig = plt.figure(figsize=(9, 9))
plot_3d(EBData_phated, sample_labels, fig)
plt.show()

同じscRNA-seqのデータでPCA, t-SNE, UMAPなどと比較してみる。

compare_vis(EBData.values, sample_labels)

t-SNEやUMAPはやっぱりクラスタ感が強く出てしまって、軌道がわかりにくい。

PHATEの実装

論文のメソッドにしたがってPHATEを実装してみる。

いろんな手法を合体させて全体が構成されているので、どこの部分の処理が可視化の改善に決定的な寄与をしているのかよくわからない。なので、いくつかのステップに区切って実装してみる。正直実装してみても各ステップの重要度というか、必然性がよくわからないけど...というかこの実装であってるのかどうかもよくわからないけど...

大きくは以下の4ステップからなる。Diffusion mapを知っている人は、ステップ2まではほとんど同じなので飲み込みやすいかもしれない。
1. Diffusion operatorの計算
* 距離行列への変換、カーネルかませて局所的アフィニティを計算、1ステップ分の遷移確率行列=diffusion operatorを構成する
2. 拡散タイムスケール"t"の決定
* 何ステップぶん拡散を進行させるかを、diffusion operatorのt乗に含まれる情報量から決定する
3. 拡散プロセスを実行し、"potential distances"を計算
* 拡散後の距離をDiffusion mapのようにDiffusion distanceで測るのではなく、新たに提案したPotential distanceで計算する。
4. Potential distanceをMDSで低次元埋め込み
* MDS(多次元尺度構成法)をつかってpotential distanceの距離関係を任意の低次元座標の距離関係に移す。

1. Diffusion operatorの計算

まず、データ全体のユークリッド距離行列を計算する。

それぞれのデータ点について、t-SNEやUMAPと同じような適応的なカーネルを作用させて、近い距離にあるデータ点どうしは大きな重み（=affinity）に、遠いデータ点どうしは小さな重みになるようなグラフ構造を作る。

ここで、全体の結果に大きく影響するパラメータ、knnとalpha（phateのオリジナル実装ではdecayと呼ばれている）が出てくる。

カーネルは普通のガウシアンカーネルだけど、t-SNEにおけるperplexity, UMAPにおけるn_neighborsのように、データ近傍の密度に合わせて適応的にバンド幅を変える。

PHATEの場合はこの適応的バンド幅を単純に、それぞれのデータ点からknn番目に近いデータ点との距離$\epsilon_k$とする。

もうひとつの工夫は、$\alpha$-decaying kernelとよばれるもの。バンド幅だけを変えると、幅が広いときかなり遠くの点までaffinityが残ってしまう（heavy-tail）。そうすると、密度の低い領域からとられた点は、他の全ての点とのaffinityがほとんど同じ値になってしまう。これを防ぐために、以下のようなカーネルを使って、パラメータ$\alpha$によってaffinityのdecayをコントロールする。

$$K_{k, \alpha}(x,y)=\frac{1}{2}exp\left( -\left(\frac{|x-y|_2}{\epsilon_k(x)}\right)^{\alpha}\right) + \frac{1}{2}exp\left( -\left(\frac{|x-y|_2}{\epsilon_k(y)}\right)^{\alpha}\right)$$

$\alpha=2$の場合、通常のガウシアンカーネルだが、$\alpha$が大きいとより急速にaffinityが減少していく。

knnと$\alpha$はどちらもグラフのつながり具合に影響を与えるので、慎重に決定する必要がある。knnが小さすぎ、あるいは$\alpha$が大きすぎてグラフがあまりにスパースだと、拡散プロセスがうまく進行しない。一方、knnが大きすぎ、あるいは$\alpha$があまりに小さすぎると、全体が均等な重みでつながってしまい、構造を捉えられなくなる。一応、PHATEはパラメータの違いにわりとロバストだと主張されているけど、どちらかを固定していろいろと実験してみたほうがいいと思う。

import numpy as np
from scipy.spatial.distance import pdist, squareform

def diffusion_operator(data, knn=5, alpha=40):
    # ユークリッド距離行列の構成
    dist = squareform(pdist(data))
    # 適応的バンド幅epsilonの計算。距離行列をソートしてknn番目の値。
    epsilons = np.sort(dist, axis=1)[:, knn]
    # alpha-decaying kernel
    kernel_mtx = np.exp(-1.* np.power(dist / epsilons[:, np.newaxis], alpha))
    # L1-normで正規化。行ごとに確率分布となる。
    l1norm_kernel_mtx = kernel_mtx / np.abs(kernel_mtx).sum(axis=1)[:, np.newaxis]
    # 対称化。
    transition_mtx = 0.5 * l1norm_kernel_mtx + 0.5 * l1norm_kernel_mtx.T
    return transition_mtx

2. 拡散タイムスケール"t"の決定

最後の重要なパラメータは拡散のタイムスケールを決める"t".

affinityに基づくランダムウォークを何ステップぶん進行させるか（=diffusion operatorを何乗するか）を決める。

拡散プロセスはデータのノイズ除去の役割も果たす。高いaffinityの短いパスでつながりあったデータ点はランダムウォークでお互いに訪れる確率が高く、低いaffinityのパスしかないような外れ値的な点は訪れる確率が低いので、拡散ステップが進むたびに前者が強調される。なので、拡散タイムスケールはノイズ除去の度合いと見ることもできて、小さすぎるとノイズがたくさん残ってしまうし、大きすぎると重要なシグナルがノイズとして除去されてしまうかもしれない。

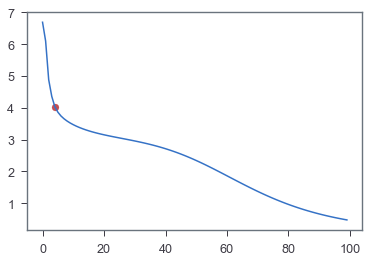
PHATEでは、データから拡散タイムスケール t を自動決定する手法として、さまざまなtでdiffusion operatorのt乗に含まれる「情報量」を調べることにより、ノイズが除去し終わって、その一方、データの本来の構造はつぶさないようなタイミングを見計らってtを決定する。

具体的には、diffusion operatorのt乗それぞれ（のsymmetric conjugate）について固有値を計算してvon Neumann entropy(VNE)を算出する。tが大きくなるとVNEは小さくなっていく。初期のVNE減少はノイズ除去によるもので、重要でない固有値は急速にゼロになる。データの構造を反映した固有値はもっとゆっくり減少していく。なので、減少率が切り替わるタイミングのtを選べば、ノイズは除去され、かつ構造はつぶれないようなtが自動的に選べる。

ここでは様々なtでVNEを計算したあと、それぞれのtの左側、右側で二本の線形回帰を実行して、合計のエラーが少なくなる点を選ぶことによってプロットの"knee point"を検出する。

from tqdm import tqdm_notebook as tqdm

def von_Neumann_entropy(P):
    # symmetric conjugate (diffusion affinity matrix)の計算
    norm_factor = np.sqrt(P.sum(axis=1))
    A = P / norm_factor[:, np.newaxis] / norm_factor
    # 固有値分解
    eig, _ = np.linalg.eigh(A)
    eig = eig[eig > 0]
    eig /= eig.sum()
    # VNEは正規化した固有値のシャノンエントロピー
    VNE = -1.0 * (eig * np.log(eig)).sum()
    return VNE

def find_knee_point(vals):
    y = vals
    x = np.arange(len(y))
    candidates = x[2:len(y) - 2]
    errors = np.zeros(len(candidates))
    errors[:] = np.nan
    # 各tごとに、左側、右側それぞれで線形回帰して、エラーを計算
    # もっとうまいやり方がありそうだけどここでは愚直にひとつずつ計算...
    for i, pnt in enumerate(candidates):
        # left area linear regression (y = ax + b)
        # 点の左側で教科書通りの最小二乗法を計算する。
        x_mean = x[:pnt].mean()
        y_mean = y[:pnt].mean()
        a = ((x[:pnt] - x_mean) * (y[:pnt] - y_mean)).sum() / np.power(x[:pnt] - x_mean, 2).sum()
        b = y_mean - a * x_mean
        left_err = (a * x[:pnt] + b) - y[:pnt]
        # right area linear regression
        x_mean = x[pnt:].mean()
        y_mean = y[pnt:].mean()
        a = ((x[pnt:] - x_mean) * (y[pnt:] - y_mean)).sum() / np.power(x[pnt:] - x_mean, 2).sum()
        b = y_mean - a * x_mean
        right_err = (a * x[pnt:] + b) - y[pnt:]
        # total error
        errors[i] = np.abs(left_err).sum() + np.abs(right_err).sum()
    # エラー最小の点をknee pointとする
    knee_ind = candidates[np.nanargmin(errors)]
    return knee_ind

def find_optimal_timescale(P, max_t=100):
    VNEs = np.zeros(max_t)
    for t in tqdm(range(1, max_t+1)):
        # それぞれのtごとにdiffusion operatorのt乗とVNEを計算。
        Pt = np.linalg.matrix_power(P, t)
        VNEs[t-1] = von_Neumann_entropy(Pt)
    knee_point_ind = find_knee_point(VNEs)
    optimal_t = knee_point_ind + 1
    fig, ax = plt.subplots()
    ax.plot(range(len(VNEs)), VNEs)
    ax.scatter(knee_point_ind, VNEs[knee_point_ind], marker='o', color='r')
    plt.show()
    return optimal_t

3. 拡散プロセスを実行し、"potential distances"を計算

Diffusion mapの場合は、diffusion operatorを固有値分解するとそのまま、diffusion distance（tステップ後確率分布の点ごとの二乗距離）を反映する座標が得られる。

だがこの距離計算だと、低い確率値の感度が低いため、遠い点どうしの距離（データの大域的構造）の情報が反映されにくい。

そこで、tステップ拡散後のdiffusion operatorについて対数変換してからユークリッド距離を計算する。これを"potential distance"と呼ぶ。新たに導入されたこの距離指標が物理的にどのような意味を持つのか、論文で詳しく説明されている（が、よくわからなかった）

def potential_distances(P, t):
    # diffusion operatorをt乗する
    Pt = np.linalg.matrix_power(P, t)
    # -log(P^t)に変換してユークリッド距離を計算
    return squareform(pdist(-1.0 * np.log(Pt + 1e-7)))

4. Potential distanceをMDSで低次元埋め込み

Diffusion mapのように固有値分解するかわりに、3で計算したpotential distanceをMDS(多次元尺度構成法)で可視化に適した低次元に移す。

まずclassical MDS(=PCoA)を使って低次元座標を計算して、それを初期値としてmetric MDSを計算する。

metric MDSはscikit-learnのSMACOFアルゴリズムで実行。

from sklearn.manifold import smacof

def mds(dist, n_components=2):
    # classical multidimensional scaling (= PCoA)
    n = len(dist)
    J = np.eye(n) - np.ones((n, n))/n
    B = -J.dot(dist**2).dot(J)/2
    evals, evecs = np.linalg.eigh(B)
    idx   = np.argsort(evals)[::-1]
    evals = evals[idx]
    evecs = evecs[:,idx]
    pos = np.where(evals > 0)[0]
    initial_coords  = evecs[:,pos].dot(np.diag(np.sqrt(evals[pos])))[:, :n_components]
    # metric multidimensional scaling (SMACOF algorithm)
    coords = smacof(dist, n_components=n_components, init=initial_coords, n_init=1)[0]
    return coords

以上のステップを実際に木構造データで実行してみる。

diffop = diffusion_operator(tree_data, knn=15, alpha=40)
optimal_t = find_optimal_timescale(diffop)
print(optimal_t)

potential_dist = potential_distances(diffop, optimal_t)
coords = mds(potential_dist)

fig, ax = plt.subplots(figsize=(12, 9))
plot_2d(coords, tree_clusters, ax=ax)
plt.show()

オリジナル実装と似たような結果が得られた。

実際はそれぞれのステップでの数値計算の安定性を高める工夫がなされていたり、省メモリかつ高速に計算するためのさまざまな工夫が施されて上記のアルゴリズムそのものが計算されているわけではなく近似的な計算をしているらしいけど、大枠としてはこんな感じっぽい。