この記事はデータ構造とアルゴリズム Advent Calendar 2019 16日目の記事です。
15日目は@minaminaoさんによる「すごいTrie」です。
17日目は@takilogさんによる「Fréchet距離の計算アルゴリズム」です。
はじめに
この記事では有名なデータ構造である赤黒木がなぜあのようなトリッキーな定義になっているのかその本質について解説します。
赤黒木の定義を見てトリッキーと思うかどうかは個人差あるかと思いますが、少なくとも僕が初めて赤黒木を学んだ時はなぜこのような定義になっているのか、そしてどうやって思いついたのか見当がつかずとても不思議に感じました。
しかし、その後赤黒木の成り立ちやその基になったデータ構造について知ると、トリッキーに見えた定義がとても自然であることを実感しました。
おそらく知っている人は当たり前に知っている内容だとは思いますが、知らない人も多くいると思いますので、この記事ではそんな赤黒木の理解を深める赤黒木の本質について紹介したいと思います。
前提知識は特にいらないですのでご安心してください(計算量の概念は少し出てきますが、この記事ではそこまで重要ではないです)。
赤黒木も定義から説明します!
赤黒木とは
赤黒木とはkey集合を保存する平衡二分探索木の1つです(高さが$O(\log n)$となるサイズ$n$の木を平衡木といいます)。
サイズ$n$のkey集合について、keyの探索、挿入、削除を$O(\log n)$時間で実行することが出来ます。
赤黒木は以下の5つの性質を満たす二分木と定義されます。
- 各ノードは赤と黒のいずれかに塗られている
- rootノードは黒
- 葉は黒(対応するkeyはnilで仮想的な葉)
- 赤ノード同士は親子にならない(以下のように言い換えることも出来る)
- 赤ノードの親は必ず黒ノード
- 赤ノードの子供は必ず黒ノード
- rootから任意の葉ノードまでのパス上の黒ノードの数はすべて一致する

画像はRed–black tree - Wikipediaより引用
上記の性質により、rootから任意の葉までのパス長を考えると、一番長いパス長は一番短いパス帳の高々2倍になることがわかります(一番短いパスは黒ノードのみを辿るパス、一番長いパスは赤ノードをたくさん辿る、黒、赤、黒、赤、となるようなパスです)。
このことから要素数$n$の赤黒木の高さは$O(\log n)$になることが示すことが出来、keyの探索を$O(\log n)$時間で実行することが出来ます。
(この記事では省略しますが、挿入、削除も$O(\log n)$時間で実行できます)
たしかにこの定義から赤黒木が平衡木となることは簡単に分かるのですが、なぜこのようなデータ構造を思いついたのか or 思いつくことが出来たのか読み取ることはとても難しいです。
赤黒木の本質は2-3-4木
結論から先に述べると、赤黒木の本質は2-3-4木です。
赤黒木は平衡木の1つである(ただし二分木ではない)2-3-4木を二分木でシミュレーションするデータ構造として誕生しました。
2-3-4木は赤黒木に比べて定義や各種操作が極めて単純で明快です。
2-3-4木を二分木でシミュレーションする上で、赤と黒に塗り分けたり、赤を連続しないという定義にすると色々と都合が良いので赤黒木はあのような定義になったのです。
2-3-4木とはなにか、赤黒木と2-3-4木はどう対応するのかを知ると赤黒木の定義の妥当性が見えてきます。
それでは2-3-4木とはなにか、赤黒木と2-3-4木はどう対応するのかについて迫っていきましょう。
2-3-4木とは
2-3-4木は平衡木であるB木の一種です。
B木は以下のように定義され、パラメータ$t=2$のときのB木を2-3-4木と呼びます。
- パラメータ$t \geq 2$を持つ
- 各ノードが保持する内部key数に上限、下限がある
- 上限:高々$2t-1$の内部keyを持つ
- 下限:少なくとも$t-1$の内部keyを持つ(rootノードは例外)
- 各ノードは内部キー数+1の子をソートした状態で持つ
- 全ての葉は同じ深さを持つ
- 木をin-orderで辿ったときのkeyの列はソートされている
- つまり任意のノードが保持するkey列(key1, key2, ...)、child列(child1, child2, ...)があったとき次のように辿ったkey列がソートされている
- child1をin-orderで再帰的に辿る, key1, child2をin-orderで辿る, key2, ...
(B木の定義はアルゴリズムイントロダクションに記載の定義を簡略化して記載しています)
2-3-4木の例。
この木をin-orderで辿ったkey列はB, C, D, F, ...とソートされている。
*上記のB木の定義はアルゴリズムイントロダクションに記載の定義を簡略化しており、また図の例のインスタンスも同書籍から拝借しています。
定義より2-3-4木の木の高さは$O(\log n)$であり、探索時間は$O(\log n)$時間で実行できることが簡単に分かると思います。
省略しますが同様に挿入、削除も$O(\log n)$時間で行なえ、その操作もAVL木や赤黒木といった平衡二分探索木の操作に比べ格段に単純な操作で実現できます。
2-3-4木は定義も実装も単純という良い点を持ちますが、B木やその他の平衡二分探索木に比べ知名度は劣ります、2-3-4木が実現場で採用されているという話も聞きません。
少し不思議ですね。
これは僕の推測ですが、2-3-4木は各ノードにおいてkeyを1-3、子を2-4持つだけの領域を確保する必要があるなど領域面で二分探索木に劣るのがあまり使われていない理由ではないかと思います。
もし、こういう場面で採用されているよという実例があったらぜひ教えて下さい。
赤黒木と2-3-4木の対応
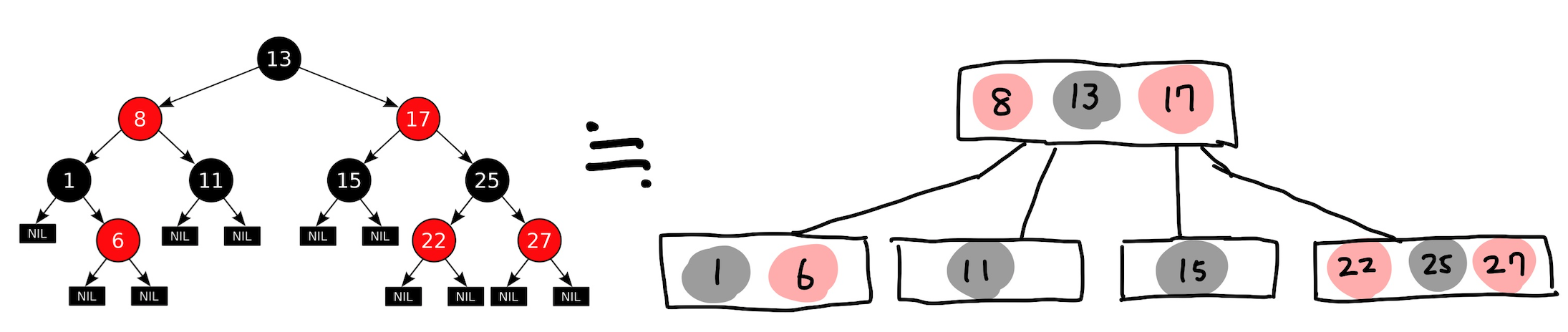
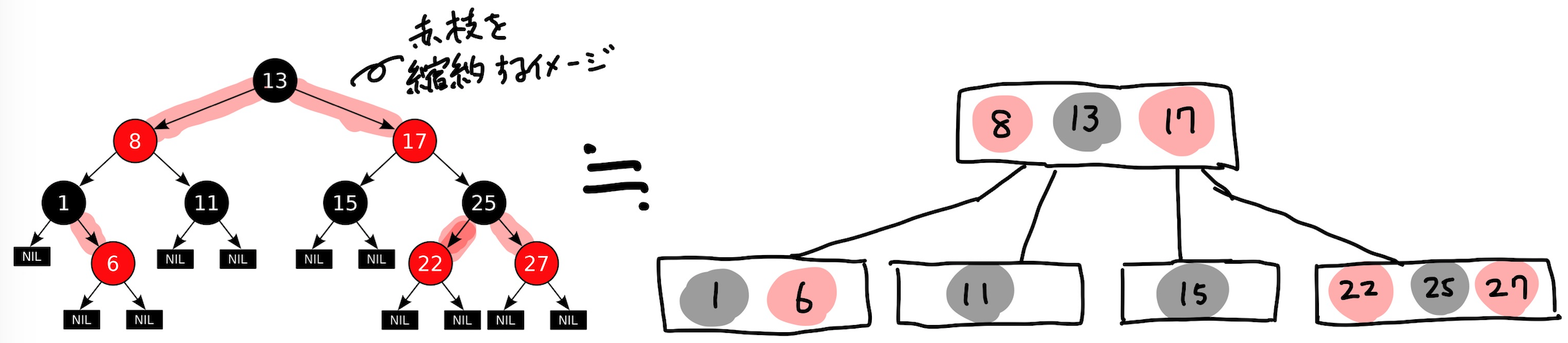
任意の赤黒木は赤ノードの親枝を縮約することにより2-3-4木に変換することが出来ます。
たとえば図の「8」と「17」の赤ノードに着目します。
これらの親枝を縮約するとrootノード「13」に近づいていき、最終的に「8」と「17」がrootノードに取り込まれるイメージです。
そうすると、変換した木では各ノードは必ず黒ノードを1つ含み、内部keyが高々1から3、子ノードが2から4となります。
また赤黒木の性質からこの木の全ての葉までの深さは一致します。
以上から任意の赤黒木について、この変換を行って得られた木は2-3-4木になることが導かれます。
つまり、赤黒木の赤ノードは2-3-4木の各ノードを二分木へと変換し、2-3-4木をシミュレーションするために仮想的に作られたノードだったのです。
おわりに
どうでしょうか、赤黒木の定義は一見トリッキーに見えますが、2-3-4木を学び、赤黒木が2-3-4木を二分木上でシミュレーションしているという本質を捉えると、その定義はとても自然に見えてくるのではないでしょうか。
本質を捉えることはとても重要であり、本質を知ることで応用範囲も広がります。
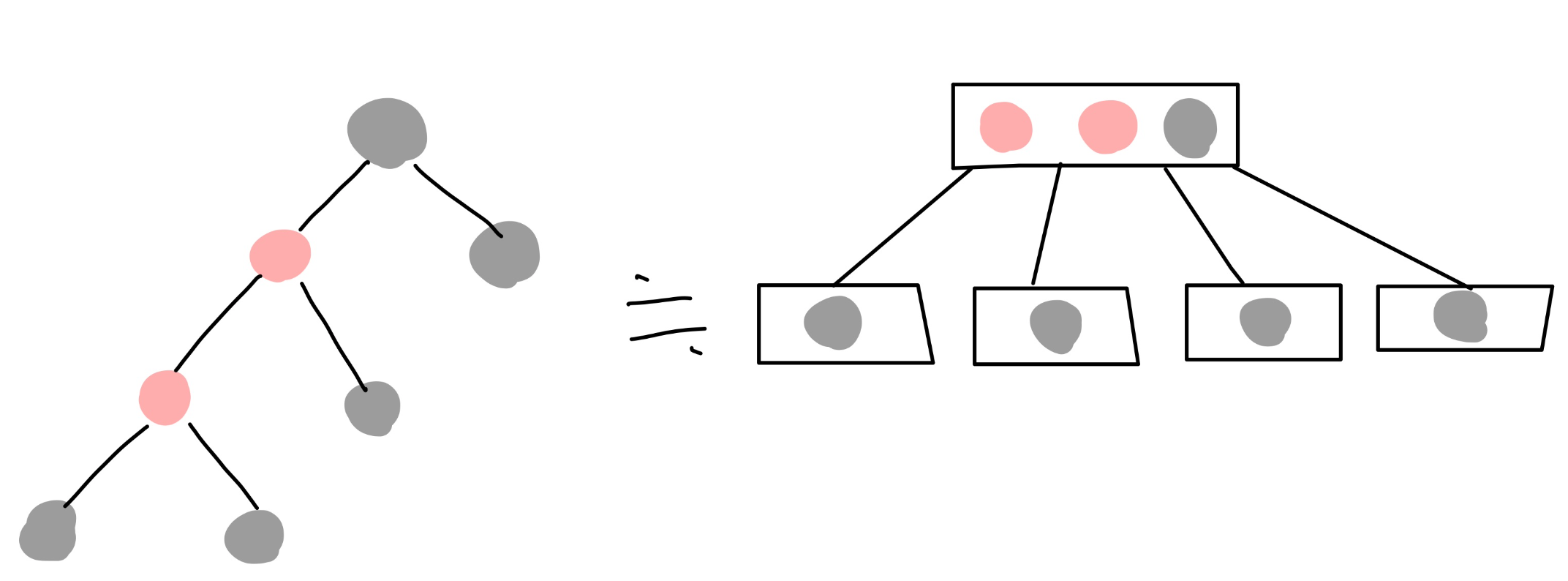
例えば、2-3-4木を二分木でシミュレーションすることが本質であれば、以下のような赤ノードが連続する構造を許容しても平衡木になることがわかります。
実際にこの構造は赤黒木をよりシンプルにした左傾赤黒木にて採用されていました1(現在は更新されこの構造は採用されていないそうです)。
二分探索木は奥が深くとてもおもしろいデータ構造です。
良い二分探索木の研究は今でもホットな研究2ですので、興味があればぜひ取り組んでみて下さい。
おまけ:周りと差をつける赤黒木の作図法とトリビア
おまけとして、上記説明した赤黒木の本質がとても分かる赤黒木の作図法とトリビアを説明したいと思います。
今から説明する作図法は僕が発明したわけではなく、赤黒木の原著論文2つにそれぞれ書いてあることです。
ただし、あまり採用されていないように思えるので、この作図法を意識すると周りと差をつける(?)ことが出来るかもしれません。
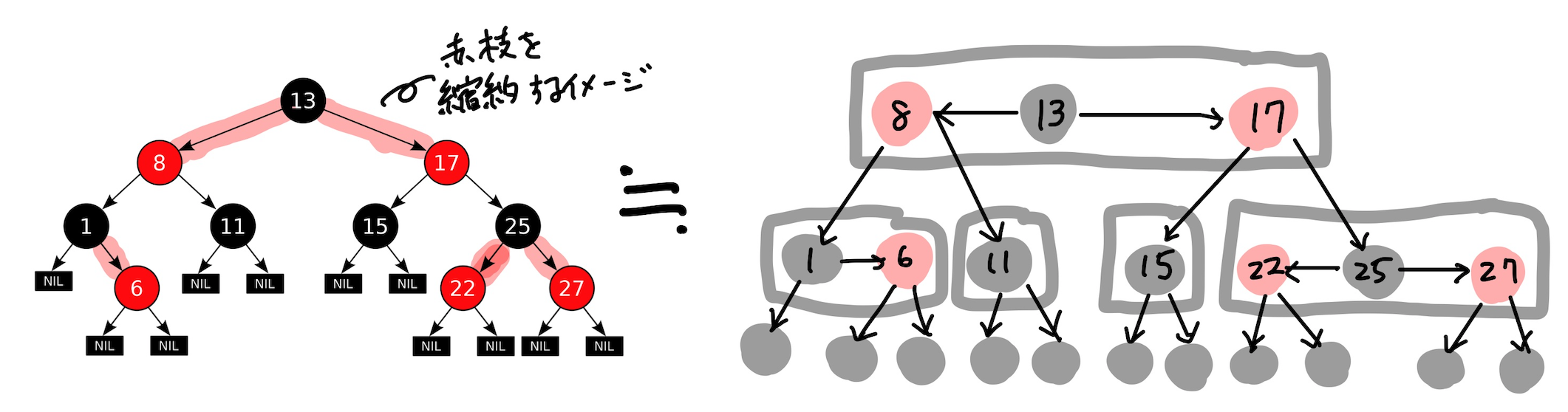
ノードを赤黒に塗るだけでなくその親枝も同じ色で塗る(Guibas and Sedgewick 1978)
原著論文でも以下のように記述されています。
It is more convenient to draw colored links than colored nodes.
(a dichromatic framework for balanced trees, Leo J. Guibas and Robert Sedgewick)
この様に表現すると赤枝を縮約することで2-3-4木に変換できることがより意識づけ出来ます。
赤枝は親黒ノードから平行に伸ばす(Bayer 1972)
rootから各ノードまでに出現する黒ノードの数を黒深さとすると、この表現にすることで黒深さが一致するノードはすべて平行に並ぶようになり、赤黒木が平衡木であることがより強調されます。
同時に、赤黒木が2-3-4木をシミュレーションしていることもよく分かる表現となっています。
赤黒木の発明者はだれ?
赤黒木の発明者はBayer(1972)だと紹介される場合とGuibas and Sedgewick(1978)だと紹介される場合があります。
どちらも正しいですし、提案されたデータ構造の本質は同じです。
提案したのはBayerが先ですが、ノードを赤黒に塗り分け赤黒木と名付けたのはGuibas and Sedgewickです。
Bayerは2-3-4木の各ノードを下方向に伸ばす枝と水平方向に伸ばす枝に変換することで二分木でシミュレーションする方法を提案しました。
つまり上記「赤枝は親黒ノードから平行に伸ばす」で述べた表現法を用いたのです。
各ノードを赤黒に塗り替えてはいませんが、赤黒木の本質はBayerが見出しました。
Guibas and SedgewickはBayerの手法をより洗練させ、赤黒に塗る方法を提案しました。
また挿入、削除時に必要な木の操作を「木の回転操作」で実現する方法も提案しました(Bayerは回転操作を用いていなかった)。
なぜ色は赤と黒が選ばれたのか
著者らが所属していたXeroxが製造するプリンタで印刷したときに赤が一番見栄えが良かったからだそうです(黒が選ばれた理由については言及されていないですが最も使われるデフォルトの色だからでしょう)。