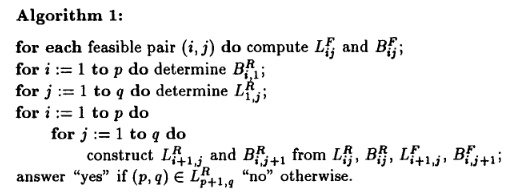LoginSignup
32
21

More than 3 years have passed since last update.

データ構造とアルゴリズムAdvent Calendar 2019Day 17
@takilog(たきたき)

Fréchet距離の計算アルゴリズム

Posted at

この記事はデータ構造とアルゴリズム Advent Calendar 2019 17日目の記事です．
16日目は @kgoto さんが「赤黒木の本質」について書かれていました．
18日目は @Akazawa_Naoki さんが担当です．

アルゴリズム系の話がガッツリと続いていますが，今日はフワっとした話です．記事中のコードはJuliaで書いています．需要はないと思いますが，一応こちらに置いてあります．

はじめに

世の中で様々な軌跡データ(GPSなど)が得られるようになって久しいですが，論文[1]を読んでいるときに，いくつかの生軌跡(細い線)を単純化した線を中心とするクラスタ(色)に分けるという手法を知りました．

クラスタリング自体は $k$-means (wikipedia) のような手法を使うとして，曲線同士の距離が分かると良いなという気持ちになりました．この記事では，そのような曲線間の距離として「Fréchet Distance」が使われていたので，計算アルゴについてまとめていくものです．

ここでは次のような問題を考えていきます．

  • 入力: 2つの曲線$P, Q$ (線分の列)，パラメータ$\epsilon$
  • 出力: frechet距離 $d_F(P, Q) \leq \epsilon$ かどうか

距離$d_F$の定義は，文献によって表記が微妙に異なりますが，だいたい次のような形です．曲線$P$と$Q$上を点が移動していき，その点を$P$から$Q$に写像させる対応関係$f$を考えます．そのinfとsupを計算するというのが距離計算の雰囲気です．曲線上の点同士の距離($||\cdot ||$の部分)は，簡単化のために平面上のユークリッド距離にしておきます．

$$
d_F(P, Q) := \inf_{f:[0,1]\to[0,1]} \sup_{t\in[0, 1]} ||P(t) - Q(f(t))||
$$

Fréchet距離は，数式は置いておくとしても，以下のような（よく分からない）例で説明されることもあります．下の図は論文[4]で著者が書いていた図です．犬の首がヤバそうですね．

find the largest distance between the man and its dog as they walk along their respective path; finally, keep the smallest distance found among these maximum distances.

もしDTW(Dynamic Time Warping)や編集距離という言葉を聞いたことがあれば，だいたいイメージできると思います．こちらのブログはDTWの計算をアニメーション化したものです．

ここからは計算方法を見ていきたいと思います．読んだ論文自体は[4]ですが，大事なのは基本的なアルゴリズムの方なので，基本アルゴリズムを論文[6]から学んで解説します．その後で，論文[4]の開発(engineering)について説明します．

アルゴリズム (Alt and Godau)

論文[6]で提案された基本アルゴリズムは，Fréchet距離の実装的な研究でよく参照されています．このアルゴリズムはおおよそ，次のような計算を行うものです．

  1. $P, Q$の各線分$P_i, Q_j$のペア毎に free-space と呼ばれる情報を計算する
  2. free-spaceを組合せ，$P$と$Q$の間のfree-spaceとする
  3. もしfree-spaceの上で$(0, 0)$から$(|P|, |Q|)$まで，monotone curveを引くことができれば，上の問題の出力としてYesを返す

3.の要件はこの業界ではwell-knownだそうです．具体的に1.や2.を計算するには，計算幾何的な計算や，離散化したあとでDP的に計算したり，再帰関数で計算したりします．とりあえずここからは，この手続きで問題が解けると信じることにします．その上で，free-spaceというものについて見ていきます．

その1. 線分同士の free-space 計算

ここでは一番簡単な場合として，線分同士の計算を考えてみます．これは次の図のような状況です．左側が線分の例，右側に描かれているものが今計算したいfree-spaceを可視化したものです．

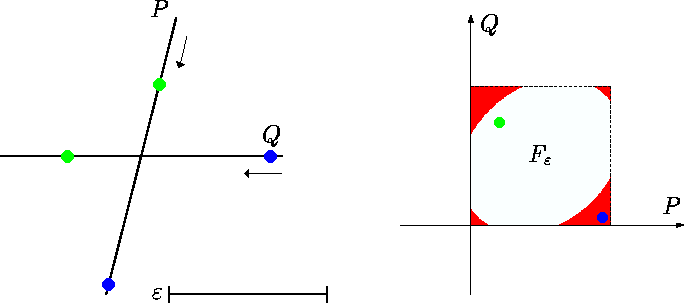
線分$P$と$Q$に対して，free-spaceは次のように定義されます．

$$F_\epsilon := \{(t_1, t_2)\in [0, 1]^2 \mid d(P(t_1), P(t_2)) \leq \epsilon\}$$

簡単ですね！図で赤くなっているところの気持ちを説明します．Fréchet距離では$\inf \sup (\cdot)$という形だったので，もしfree-spaceを計算したときに$(t_1, t_2)$に対応した頂点同士の距離が既に$\epsilon$を超えていれば，どんなに頑張って$\inf(\cdot)$を計算してもダメそうですね．そのためfree-spaceを用いて最悪のケースだった場合の情報を収集し，白い部分を見ていけば，上の決定問題が解けそう，というのがアルゴリズムの考え方です．

具体的に$F_\epsilon$を計算する場合は離散化するか，点と線分の距離を計算幾何的に求めて$\epsilon$-近傍に線分や頂点が含まれるかなどを使って判定するようです (あまり詳細は書かれていませんが)．

とりあえず幾何は怖いので，離散化してペアワイズに計算してみます．こうなると，ほとんどDTWですね．おそらくアドベントカレンダーを読むような人だと「やるだけ」の実装でしょう．ここでは上の図を模擬した曲線を作ってやっています．

# P, Q
x = 0.3;
P = [(x, 1.0), (-x, -1.0)];
Q = [(1.0, 0.0), (-1.0, 0.0)];
ϵ = 1.08;

# 離散化
n = 20;
δ1 = (L1[end][1] - L1[1][1], L1[end][2] - L1[1][2]) ./ n
δ2 = (L2[end][1] - L2[1][1], L2[end][2] - L2[1][2]) ./ n
Fϵ = zeros(Float16, n + 1, n + 1);
lx = [(L1[1][1] + δ1[1] * i, L1[1][2] + δ1[2] * i) for i in 0:n]
ly = [(L2[1][1] + δ2[1] * i, L2[1][2] + δ2[2] * i) for i in 0:n]

for dx in 1:n+1
    xi = lx[dx]
    for dy in 1:n+1
        yi = ly[dy]
        diffx = xi[1] - yi[1]
        diffy = xi[2] - yi[2]
        dxy = sqrt(diffx ^ 2 + diffy ^ 2)
        Fϵ[dx, dy] = dxy <= ϵ ? 0.0 : 1.0
    end
end
F = transpose(Fϵ);  # heatmapで可視化するために転地した

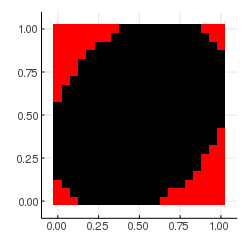
こうして計算した$F_\delta$を可視化すると次のようになりました．だいたい再現することができましたね．

その2. 曲線同士の計算

上に線分同士の$F_\epsilon$を計算することができたので，これを$P, Q$を構成する線分の個数$|P|, |Q|$分だけ繰り返してつなげていけば，曲線$P$と$Q$の間のfree-spaceを計算できます．各セルでの計算を離散化してしまったので，単純にfor文で繰り返すだけですね．

まず先に，論文などで出てくる繰り返して計算した結果のfree-spceをチラ見してみます．

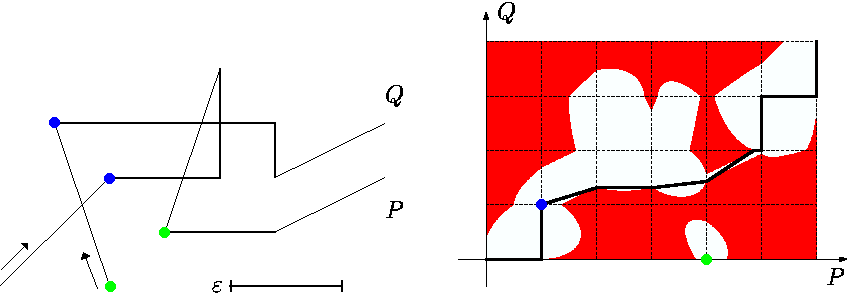
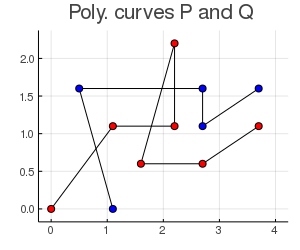
  • 左: $P, Q$
  • 右: 赤白の領域 (free-space)，$(0, 0)$から$(|P|, |Q|)$までのmonotone curveの例（黒線)，これが存在するので，この場合は$\delta_F(P, Q) \leq \delta$という判定．

上の実装を利用して，似た例題を模擬して再現した実装の結果を並べてみます．若干離散化が雑な気がしますが，離散化を細かくするとだいたい同じような図になりそうですね，めでたしめでたし．

入力 (論文をマネ) 出力 (free-space)

3. free-space上でのmonotone curve判定

ここまでで必要そうな情報は計算し終えました．次はこれを使って決定問題を解きたいです．今，信じている我々の考え方によれば，「free-spaceにおいて左下から右上に到達し，赤色の領域に踏み込まないようなmonotone curveがあるかどうか」によって，決定問題を解くことができます．

なおいくつかの論文では，この領域をreachable spaceと呼んでいます．定義はだいたい次のように書いてあります．

$$
R = \{(p, q) \in F\mid \text{there exists a monotone path from }(1, 1)\text{ to }(p, q)\}
$$

繰り返しになりますが，我々の信じていることは以下の命題です．

$$
d_F(P, Q) \leq \delta \text{ iff } (|P|, |Q|)\in R
$$

これまでの計算で，上の式の$F$は計算が終わっているので，後は$R$を計算して，上の判定式を実装すれば良いことになります．$F$から$R$を計算する操作は，正直どの論文にも詳しく疑似コードレベルでは書いていないので困ります (もしわかりやすい説明がある資料を見つけた人は，twitter @cocomoff まで教えてくださると喜びます)．

仕方ないので，$R$の計算について論文で出てくる図を見てみることにします．

この□はある線分ペア$(i, j)$に関するfree-spaceです．既存の$R$を計算するアルゴリズムは次のように構成されているようです．

  1. セルの左側($L_{i,j}$)，下側($B_{i,j}$)，右側($L_{i+1,j}$)，上側($B_{i,j+1}$)を求める
  2. セル左側・下側のreachableな線分を求める (これを入力と呼ぶ)
  3. 1.と2.で得られた6つの情報から，右側と上側のreachableな線分を求める (これを出力と呼ぶ)
  4. このような計算を左下から右上へ繰り返す (入力から出力を求めていく)．

難しくなってきました (弱い)．実際のアルゴリズムは次のように書かれています．この3.の操作ですが，論文によってはcell propagationなどの名前がついています．もう少し書いておいてほしいです．

3'. 再現実装

残念ながら論文や世の中の実装だけではcell propagationの実装がよく分かりませんでした．そのためここは想像で補った適当な実装をやります．各セルの$F$の計算は離散化されており，既にfree-spaceが求まっていることから，行列上に$d(P(t_1), Q(t_2))$などが格納されています．

これを眺めて，次のような気持ちで実装しました．今知りたいのはmonotone curveによって今考えている点に到着できるかどうかです．つまり$x$軸，$y$軸について減少するような曲線でなければOKなはずなので，

  • 左側がreachableであれば，右側もreachable ($x$軸方向に+1)
  • 下側がreachableであれば，上側もreachable ($y$軸方向に+1)
  • 左下がreachableであれば，右上もreachable ($x$軸と$y$軸ともに+1)

という風に考えればたぶんそこそこ合っているでしょう．論文の図を確認すると，考え方はそんなに間違ってなさそうです．左がfree-space，右がreachable spaceです．

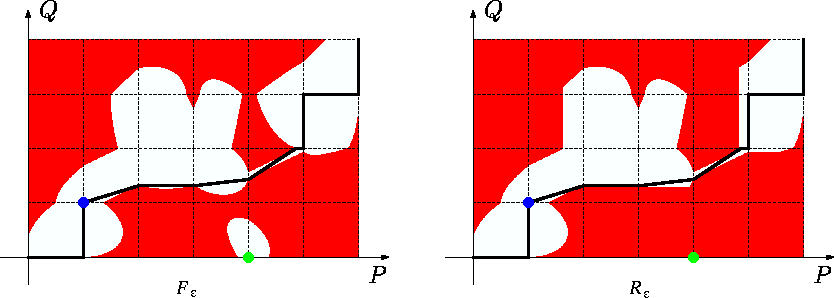
これを実装すると次の結果が得られました．色が雑ですが，左側が計算したfree space，右側が計算したreachable spaceで，論文の図とだいたい合っていてOKっぽいですね．信じましょう．

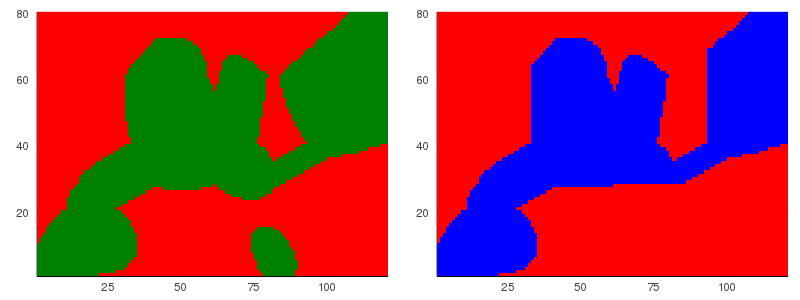
ところでここまででの計算では，線分$P_i, Q_j$のペアについてセル計算を行っていました．私は離散化して計算したのでこのような形の実装ですが，上に述べたとおり似たような感じで再帰関数としてこれは実装できます．つまり入力$P, Q$を受け取り，これを適当に半分ずつぐらいに分割しながら計算をすれば良いです．たぶんね．

ちなみに再帰呼び出し実装を行った際，現在の入力を一般にボックスと呼び（矩形領域のこと），もしボックスが再帰の末端である$(i, j)$ペアに相当する地点であるとき，これをセルと呼びます．そのため，上のあるペアに対する厳密計算をcell propagationと呼ぶのですね．

アルゴリズム・エンジニアリング (Bringmann et al. 2019)

ここまででFréchet距離の計算について完全に理解したので，最新の手法の一つである[4]を見ていきましょう．ただしここからは実装ではなく，雰囲気だけ解説していきます (実装はなし)．[4]では上に説明したとおり，$P, Q$が与えられたときにこのreachable spaceの計算を再帰的に部分曲線に対して呼び出します．そのため，

  • 呼び出された部分呼び出しが，もし意味のないセルであれば，計算を怠けたい
  • あるセルの入力がreachableでなければ，出力はreachableでない

など，事前に不必要な計算をやらないという処理を行います．このような開発(そのためタイトルにengineeringとついている)を真面目に行って，良い手法を構築してベンチマークしたというのが[4]の内容です．ここでは，上のアイデアを図を見ながら見ていきます．

フィルタリングその1

上の方でcell propagationという話がありましたが，cellの入力が空集合であるとき，monotone curveは発生しようがないとは上に述べたとおりです．分かりやすい例が論文のFigure3にあるため，見てみます．

  • 左上のボックス: 入力(左)と入力(下)が赤色 = 空集合．そのため出力(上)と出力(右)も赤色になる．
  • 右のボックス: 同様

image.png

フィルタリングその2

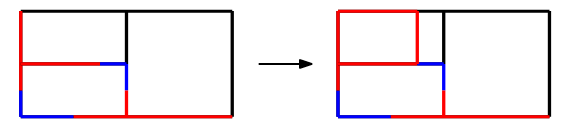
上の話だと都合よく入力が空になっているボックスがあったので助かりましたが，実際はボックスの左側，下側の表す範囲の中間地点から入力が入ってくる (これはmonotone pathが引けそうな場所がある，という意味です) ことがあります．

このとき，ボックスをうまく分割し直すと，計算範囲が縮まって有利になります．このように，現在再帰呼び出しで呼び出されたボックスを計算し直す操作がルールその2です．Figure4を見ると雰囲気が分かると思います．左上のボックスは，ボックスをshrinkしたことで，赤色のボックスが誕生しました．

フィルタリングその3

だんだん難しくなります．

これまではボックスをまるごと考えていましたが，これまでの例を思い返すと，本当に計算に寄与しているのはボックスではなく入力や出力の部分な気がします．これを（そのままですが）インターバルと呼びます．数式で書くと${p}\times [q, q']$や$[q, q']\times {p}$のようになっている潰れたボックスがインターバルですね．当たり前ですが，全てのボックスやセルは4つのインターバルで構成されています．

今，$F$を持っています（私の実装では離散化されていますが，とりあえず$F$です)．そこで，$F$とインターバル$\mathcal{I}$の共通部分を考えます．もし$\mathcal{I}\cap F$が再びインターバルになるとき，これをsimpleなインターバルと呼びます．なぜこのような考え方が重要になるのでしょうか？正確には分からないので推測ですが，フィルタリングその1やその2で見たように，今考えているボックスが「ちょうどよく切れていれば」「周辺のインターバルが既にreachable or notが計算されていれば」，余計な計算が少なくなりそうな傾向があります．そのため，今持っているボックスをうまく切り分けたい．そして「どのインターバルがまだ決まっていないのか（freeなのか）」を決定したい．これがルール3の背景だと予想しています．

さて具体的なルールを見てみます．ルール3は3つの操作があります．またここでは上の出力に位置するインターバルだけを見ていますが，右の出力についても同様に計算します．まずは論文の図Figure6を貼ってから意味を見ていきます．

  • aは，上の出力が空の場合です．上に出力が出ていかないとすぐに分かりました．
  • bは決まっていない点と，決まっている点がインターバルに混ざっている場合です (緑色が決まっていない=free)．再帰呼び出しの中で左側は既に計算されるようになっているため，この情報を用いて上のインターバルを左からreachableに埋めます．
  • cはインターバルの途中にfreeが入っている場合の状態です．bと似た形で，既に以前の再帰呼び出しで下側の計算が終わっているとします．そこで上の緑色の部分を青く塗るためには，その左端の真下に相当する入力が青色である必要があります (monotoneでつなぐ必要があります)．

以上です．このように見ていくと，上でした離散化実装もだいたい合っている気がしてきますね！（合っててくれ！）．

どうなるか

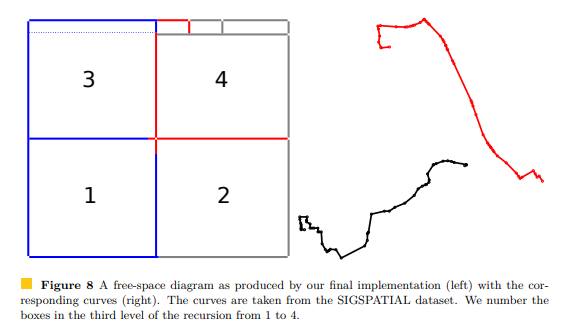
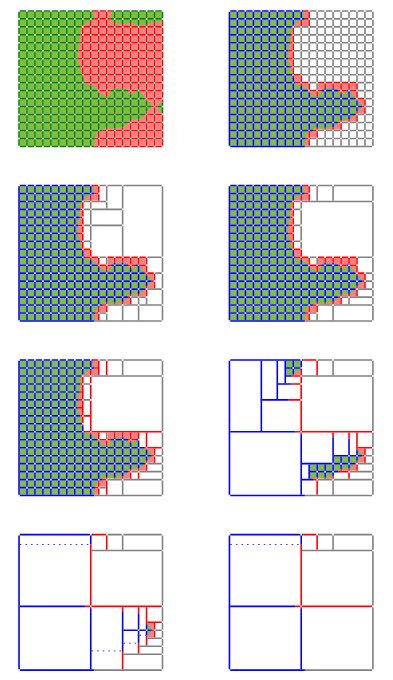
ここまでで，ボックスを再帰呼び出しで切ったりスキップしたりしながら計算する手法のアイデアを説明しました．具体的な計算がどのようなボックスの分割で行われるのか，例を論文から持ってきて終わりたいと思います．例題はFigure 8のものです．ちなみに左側の番号は再帰計算の順番です．左下から右上へのmonotone curve判定を行うので，左と下と左下は先に計算しておく必要があります．まぁDPのDTWと一緒ですね．

fig8.png

この例に対して，

  • free space
  • reachable space
  • ルール1
  • ルール2
  • ルール3a
  • ルール3b
  • ルール3c
  • ルール4

を順番に適用した結果，再帰呼び出しの計算で実際に計算判定される様子が次のFigure 9になります．徐々に再帰呼び出しの回数が減っていくことが分かります．つまり，セルが細かく区切られる前に，計算が諦められています．左上と右下を比べると，だいぶキュっとしました．

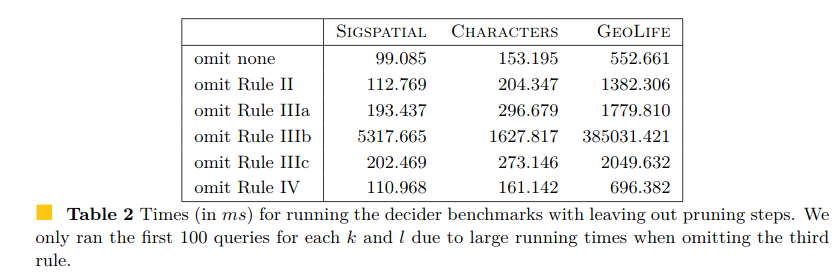
結果まとめ

論文の内容は他にもありますが，上の話でそれぞれのルールがどれぐらい効率化に寄与したかを見てみます．論文のTable 2です．全てのルールを適用した結果 (omitting none)と比較すると，ルール3が計算時間の減少によく効いているようですね．

まとめ

これで曲線の距離計算(の一部)のプロになりました (嘘です)．

参考文献

32
21
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
32
21