14日目の記事は @niuez_ さんの「動的木上の最小シュタイナー木をtoptreeで解く」でした。
16日目の記事は @kgoto さんの「赤黒木の本質」です。
はじめに
こんにちは。この記事では、コンピュータの至るところで使われている木構造 trie について紹介します。ざっくり言うと、trie は文字列の集合を木構造として表すことで高速に検索ができるデータ構造です。キーバリューストアとしても使われます。
今回は trie の応用例として、Merkle Patricia trie も簡単に紹介します。trie を省メモリ化した Patricia trie に、分散システムでデータの改変を効率的に検出するために用いられる木構造 Merkle tree を組み合わせたものです。
数学的な難しい話はほぼありません。
Trie (Prefix Tree)
突然ですが、みなさん検索エンジン使ってますよね。
例えば、「アルゴリズム」と検索するとき、「アルゴ」まで打つと「アルゴリズム」「アルゴリズム体操」「アルゴンガス」などの単語がサジェストされます。
この自動補完、trie で出来てます。
自動補完は他にも、スマホの予測変換やブラウザのアドレスバー、ターミナルでのコマンド、IDEでも見ますね。前方一致検索とも呼ばれます。
自動補完以外にも、
- URLやIPアドレスのルーティング
- スペルチェック
- 形態素解析器
- データ改変の検出
などなど様々なところに使われます。
文字列処理に欠かせない trie ですが、構造自体はとてもシンプルです。Pythonで20行くらいで実装できます。
例
例えば、以下のようなキーとバリューのペアを決めます。
| to | tea | ted | ten | A | i | in | inn |
|---|---|---|---|---|---|---|---|
| 7 | 3 | 4 | 12 | 15 | 11 | 5 | 9 |
「to」がキーで「7」がバリューです。これを trie で表すと下図のようになります。
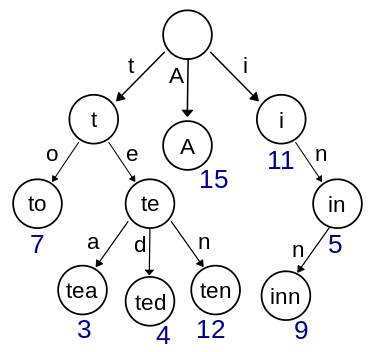
Trie - Wikipediaより引用
ノードの中に書かれている「tea」や「in」がキーであり、ノードの下に書かれている「3」や「5」がキーに対応する値です。
あるノードのキーは、その親ノードのキーに、親ノードから伸びる有向辺に書かれている文字を、付け足した文字列です。実際には、ノードには直接キーが保存されず、そのノードに到達するまでの辺のラベルの列がキーになってます。
接頭辞がノードと対応するので prefix tree とも呼ばれます。
計算量
計算量は色々な表現をすることが可能ですが、ノードの分岐は高々アルファベットの種類数なのでこれを定数とすれば、$ m $を文字列の長さとして以下の操作が$ O(m) $で出来ます。(アルファベットの種類数を考慮すると$\log$が付きます。)
- 文字列の検索
- 文字列の挿入
- 文字列の削除
- 辞書順で前・次の文字列は何か
空間計算量は挿入された文字列の長さの総和を$ M $として$ O(M) $です
どれだけ文字列を挿入しても検索・挿入・削除の計算量は変わりません。
コード
あくまでイメージとしてですが、Pythonのソースコードは、以下のようになります(Pythonのdictionaryはソートされないので注意です)。
class Node(object):
def __init__(self) -> None:
self.children = {}
self.value = None
def find(node, key):
for c in key:
if c not in node.children:
return False
node = node.children[c]
return node.value
def insert(node, key, value):
for c in key:
if c not in node.children:
node.children[c] = Node()
node = node.children[c]
node.value = value
Trieに関する基本事項は以上になります。
応用
以下、応用例を3つ紹介します。
正規表現から置き換え
キーワードリンクとは、文章にあるキーワードが含まれていたらリンクする機能のことです。はてなブログなどで使われていますね。このキーワードリンクは trie で高速に実現できます。
ちなみに、ISUCONというWebサービスの高速化を競うコンテストがありますが、ISUCON6の予選で出題されたサービスにキーワードリンク機能がありました。初期実装ではキーワードリンクが正規表現で実装されており、その処理がボトルネックになっていたので、その処理をtrieに置き換えることで高いスコアを得れました。
また、URLルーティングにも使えます。Webサービスにおいて、以下のようなURLのパターンリストがあり、
/posts/posts/:id/items/:id
あるパターンにマッチするURLを検出したいときが多々あります。簡単なものであれば正規表現で十分ですが、パターン数が多くなってくると、そのパターン数の数に応じて処理時間が多くなります。Trie を使えば、パターン数が増えても高速に処理することができます。
Binary trie
競プロだと、以下の機能を要求する問題がよく出題されます。(例: B - XOR Spread)
- $ \mathrm{insert}(x) $: 集合に非負整数$ x $を追加する
- $ \mathrm{find}(y) $: 集合の中で非負整数$ y$ とXORして最も小さくなるような要素を見つける
これは非負整数を2進数の文字列としてみて構築した trie を用いることで出来ます。Binary trie とも呼ばれます。
Binary trie は、さらに、
- 連続する部分列のうち要素を全てXORした値が最大になるようなものを見つける
- 連続する部分列のうち要素を全てXORした値が、ある値Kより小さいものの個数を見つける
などができます。
Merkle Patricia Trie
Patricia trie と Merkle tree を組み合わせたものが Merkle Patricia trie です。
Patricia Trie (Radix Tree)
Patricia trie は trie における無駄な頂点をまとめたものです。
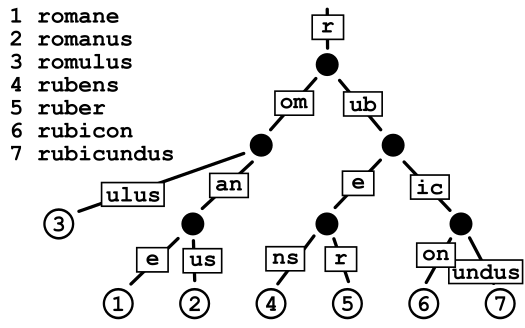
Radix tree - Wikipediaより引用
例えば、rubicundus の ulus の辺が、trie だと一文字ずつバラバラに表現されますが、Patricia trie ではまとめられます。これにより省メモリ化が実現できます。
Merkle Tree
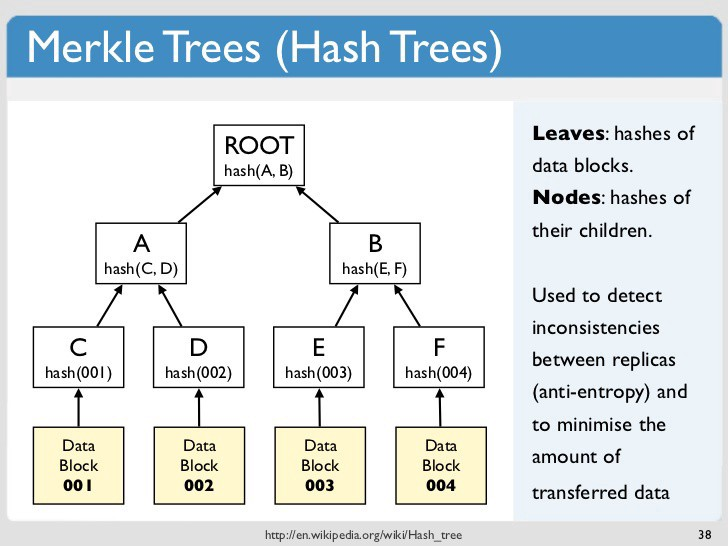
Merkle tree は、データが完全であるか(攻撃者によって改竄されていないか・偶発的な事故により改変されていないか)を低コストで検証できる木構造です。P2Pネットワークなどの分散システムなどで用いられます。ブロックチェーンでトランザクションの検証をしたいのであれば、トランザクション全てを含むブロックの情報を丸々使うこと無く、Merkle tree の情報の一部とブロックチェーンのブロックヘッダー(と呼ばれるブロックの概要みたいなもの)を用いるだけでトランザクションの検証ができます。
一番下にある黄色いブロックがデータです。このデータブロックをハッシュ化したものがC,D,E,Fの値になります。$ C = \mathrm{hash}(001) $です。Merkle tree はこれを葉とした二分木を構成します。C,D,E,Fより上のノードは子を2つ持ち、子のハッシュを結合したものを更にハッシュ化したものがノードの値になります。$ A = \mathrm{hash}(C || D) $です($||$は結合)。この処理を根まで続けます。根のハッシュのことをルートハッシュと呼びます。
ブロックチェーンでは、ルートハッシュがブロックヘッダーに刻まれます。ブロックヘッダーの情報が正しいと保証するなら、あるトランザクションがブロックに含まれるかを検証したいときは、そのトランザクションに関連のあるハッシュのみ入手し、ルートハッシュを計算し一致するか確認することで、検証できます。
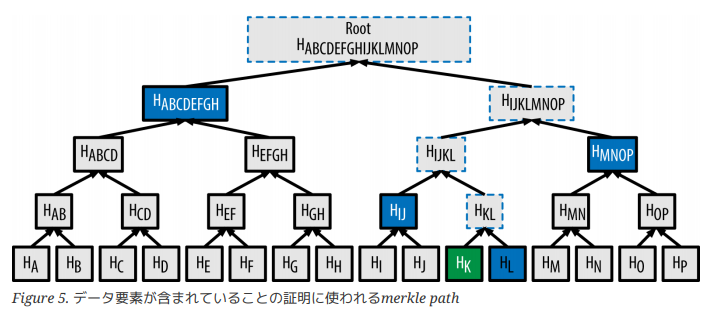
Mastering Bitcoin より引用
上の図だと、緑のハッシュの検証の際、青のハッシュのみでルートハッシュを計算できます。
ブロックチェーンをちょっとだけ利用したいのに、何百GBにもなるデータをダウンロードして使わなければいけないのは嫌なので、このような仕組みが重宝されます。
Merkle tree はWeb上に詳しい資料がたくさん転がってるので詳しく知りたい方はそちらを参照してください。
Patricia Trie + Merkle Tree
Patricia trie はキーバリューストアとしても使えました。この Patricia trie を分散システムで用いるとき、データが改変されていないかを高速に検証できるようにしたいです。Patricia trie の各ノードに対して Merkle tree のようにハッシュを計算することでこれを実現できます。Merkle Patricia trie と呼ばれ、Ethereum で使われています。
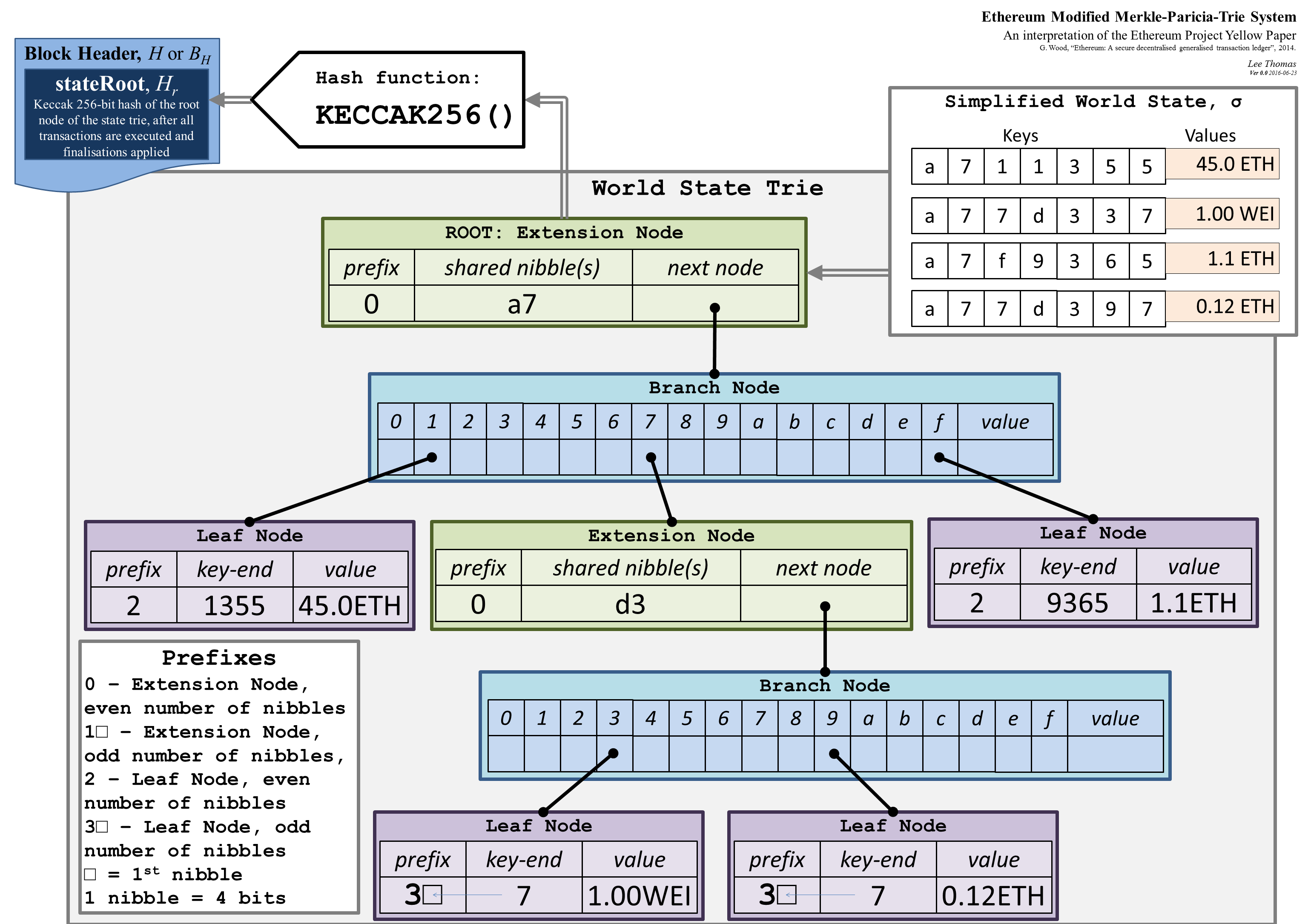
https://i.stack.imgur.com/YZGxe.png より引用
Ethereum では、トランザクションはブロックチェーンの状態など様々なデータを Merkle Patricia trie で管理します。厳密には、extension node という新しいノードタイプを加えた modified Merkle Patricia trie と呼ばれるデータ構造が使われています。
図は、キーをアカウントのアドレス、バリューをアカウントの状態とした modified Merkle Patricia trie です。world state trie と呼ばれます。キー「a711355」に対しては「45.0 ETH」が、「a77d337」に対しては「1.00 WEI」が対応しています。ブロックチェーンには world state trie の情報は自体は書き込まれず、ルートをkeccak256でハッシュ化された値がブロックヘッダーに書き込まれます。他にもトランザクションやトランザクションレシート、ストレージなどの管理に trie が使われています。
おわりに
良い感じの図をいっぱい作って良い感じに説明しようと思ったんですが、色んな〆切に追われて出来ませんでした。あとで足すかもしれません。
Trie が関連するアルゴリズムは他にも沢山あります。Aho–Corasick algorithm、x-fast trie、簡潔trie、オートマトンとの関係とか面白いです。あと Patricia trie だけでなく他のデータ構造を Merkle 化したらどうなるか考えるのも面白いかもしれません。
最後まで読んで頂きありがとうございました。