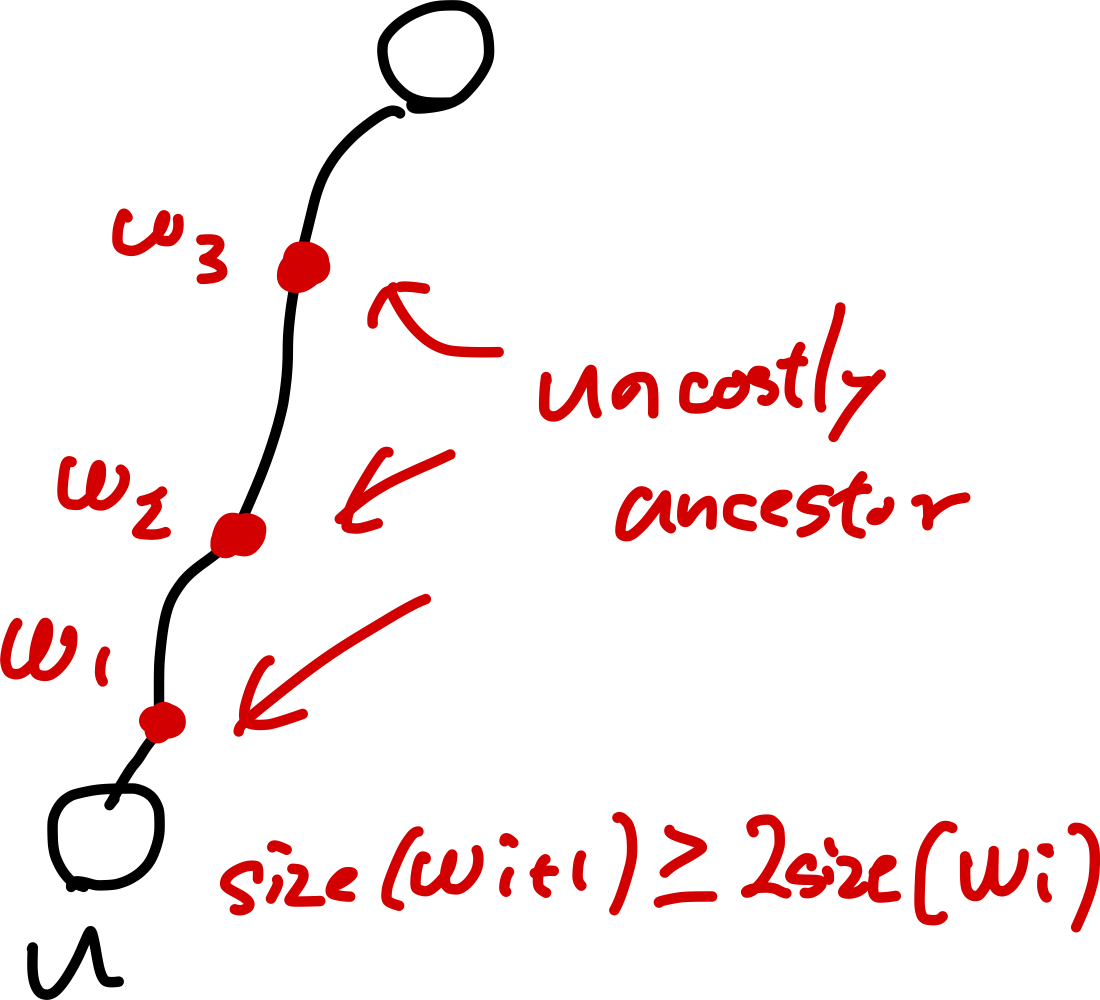注：この記事は以前勉強会で使った資料をほぼそのままで公開しています。
あまり読ませるような文章にはなっていないのでご注意ください。
はじめに
- この記事ではLCP配列の色々な構築アルゴリズムの紹介と、アルゴリズムで使われているreducible, irreducibleという面白い性質を紹介する
- この性質を使うことで次のようなメリットが有る
- LCP配列を高速に計算できる
- LCP配列を簡潔に表現できる
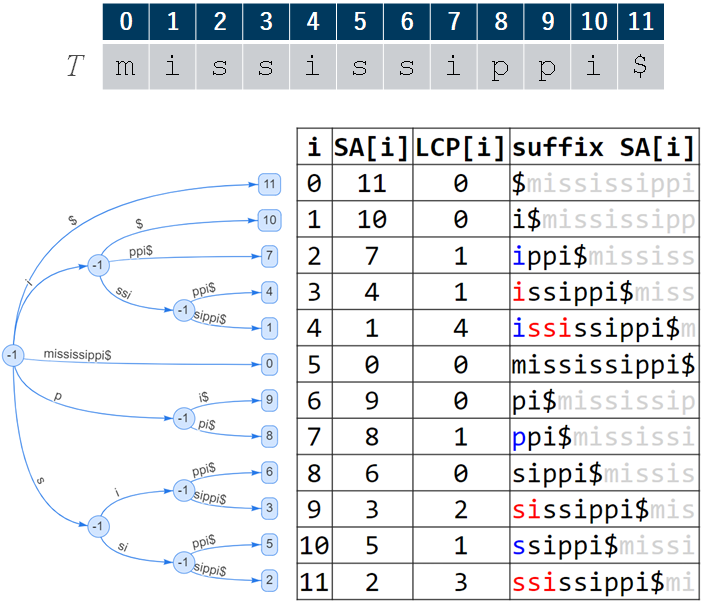
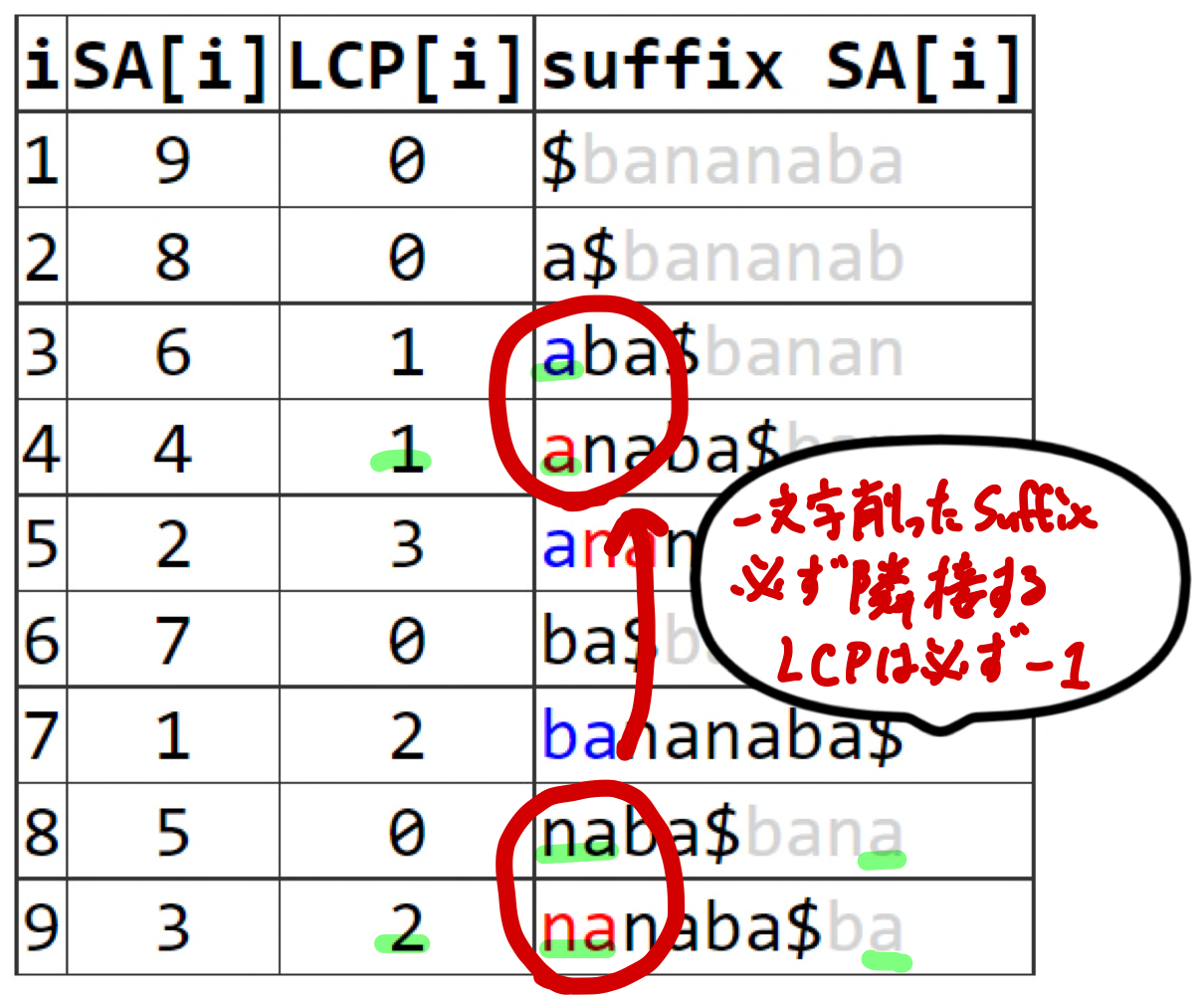
Longest Common Prefix Array
$$LCP[i]=lcp(T_{SA[i]}, T_{SA[i-1]})$$
- LCP配列：Suffix Array (SA)上の隣接するsuffixのlcpの長さを保存した配列
- ここで$T_i=T[i\ldots n]$
- $lcp(x, y)$: $x$, $y$のlongest common prefixの長さ
- Suffix Tree (ST) ≒ SA + LCP
- Suffix Treeは強力だが$T$の数十倍の領域を必要とする
-
SA + LCPはSTと同等の機能でSTよりも省領域でうれしい！
- といっても$T$の10倍ぐらいの領域が必要だし、Suffix Treeと本当の意味で同等の機能を得るためにはRMQなど他の補助データ構造が必要だったりするので領域はそれなりに必要
- 実用的にはSA, LCPをベタな整数配列として保存するのではなく、簡潔表現として保存し使ったりする
- ということでSA, LCPを高速、省領域で計算することはとても重要
- この記事ではSAがgivenとしてLCP配列の構築方法を取り扱う
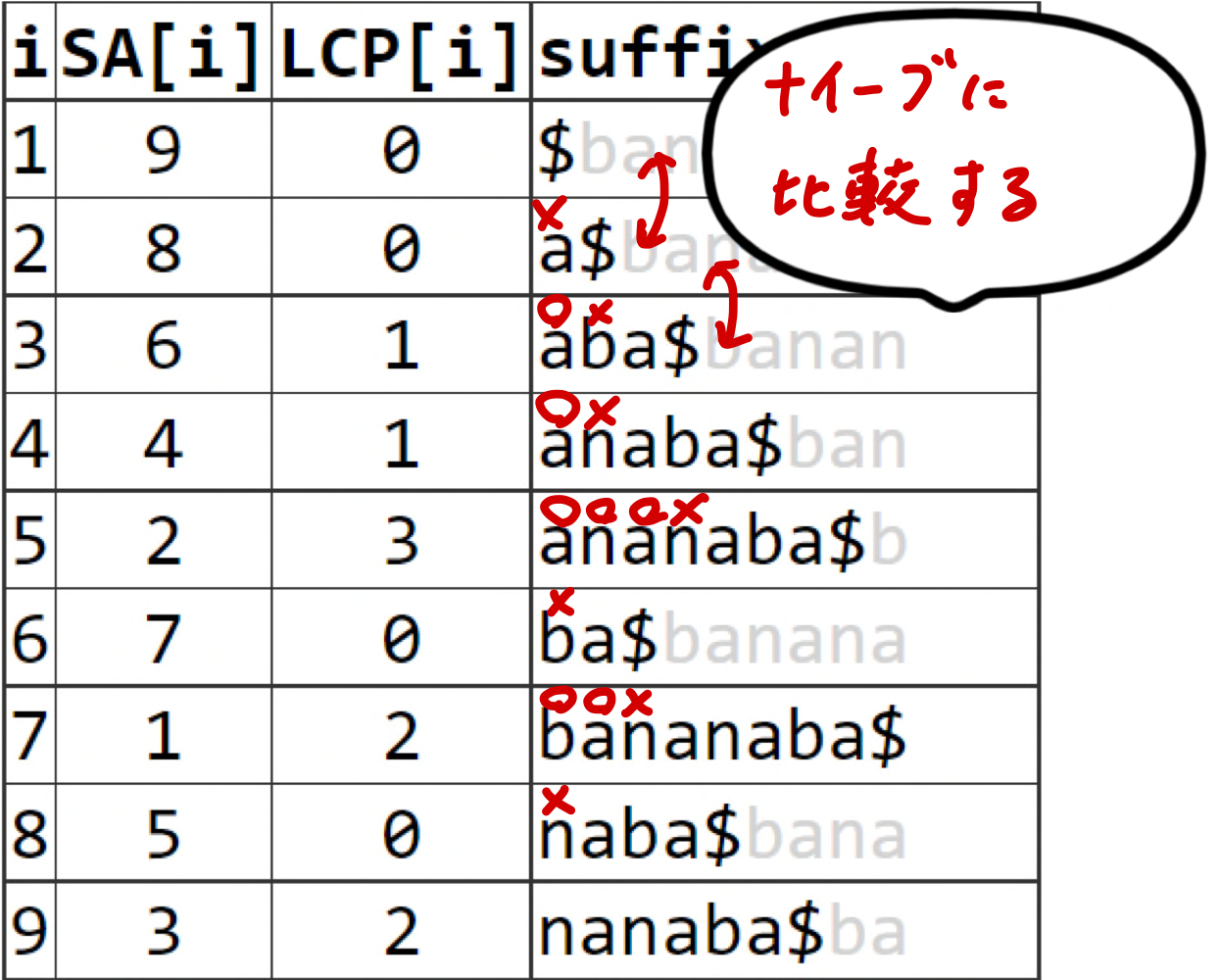
ナイーブアルゴリズム
- $LCP[i]$を先頭から順番に計算する
- $LCP[i]$の計算は$O(n)$なので全体で$O(n^2)$時間
- おそい！
# LCP配列の構築
# ここでTは文字列、SAはTのSuffix Array
def lcp_naive(T, SA):
n = len(T)
LCP = [0 for _ in range(n)]
for i in range(1, n):
i1, i2, l = SA[i - 1], SA[i], 0
while i1 + l < n and i2 + l < n and T[i1 + l] == T[i2 + l]:
l += 1
LCP[i] = l
return LCP
# Suffix Arrayの構築
def sa_naive(T):
sa = list(range(len(T)))
sa.sort(key=lambda i: T[i:])
return sa
- 高速に計算するためにはどうすればいい？？
- うまい性質を見つけて$LCP[i]$の計算の一部またはすべてを省略する
Kasaiアルゴリズム (Kasai+, 2001)
Suffix Treeを経由しないでLCP配列を線形時間で構築できることを示した初めてのアルゴリズム
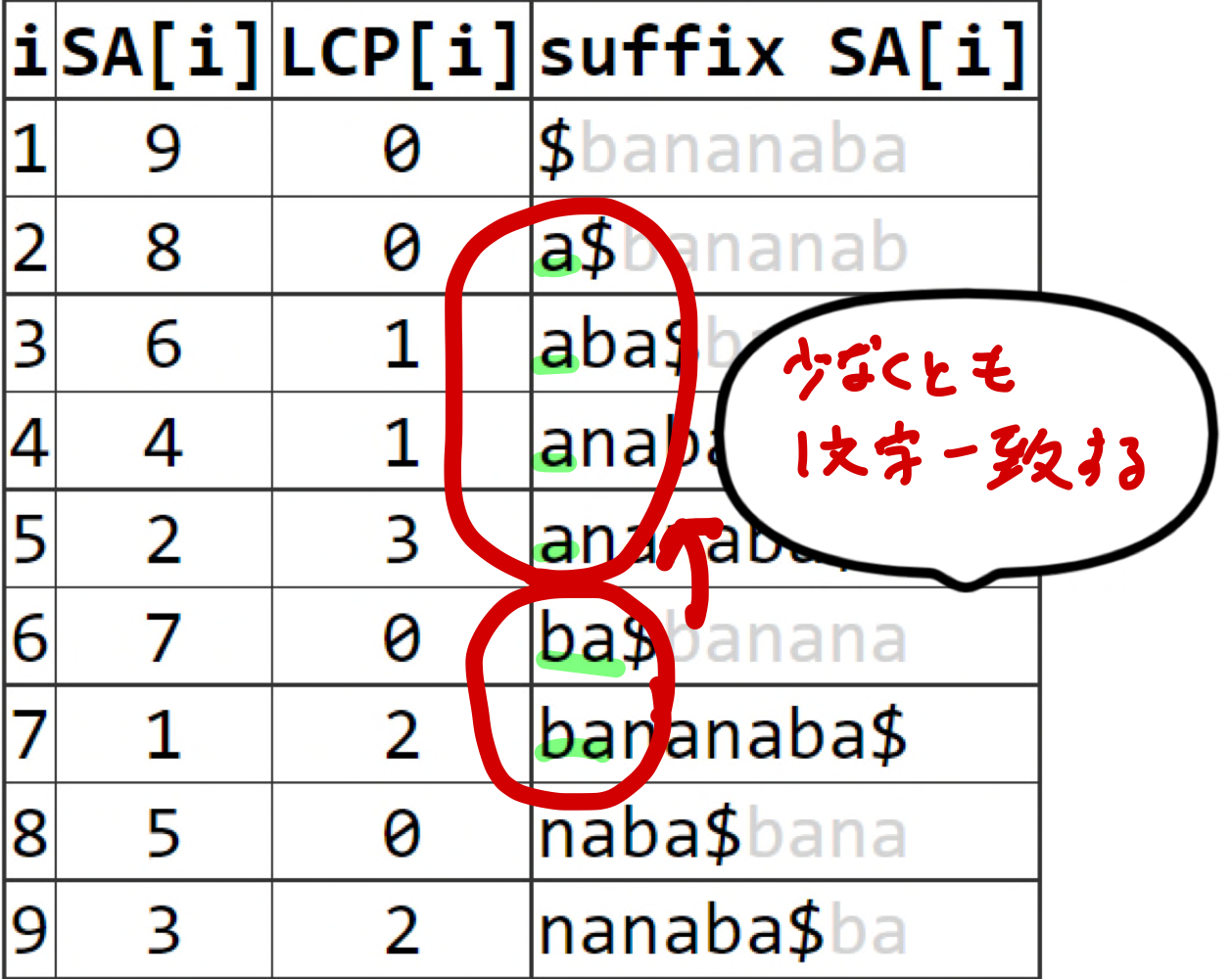
- 重要な性質
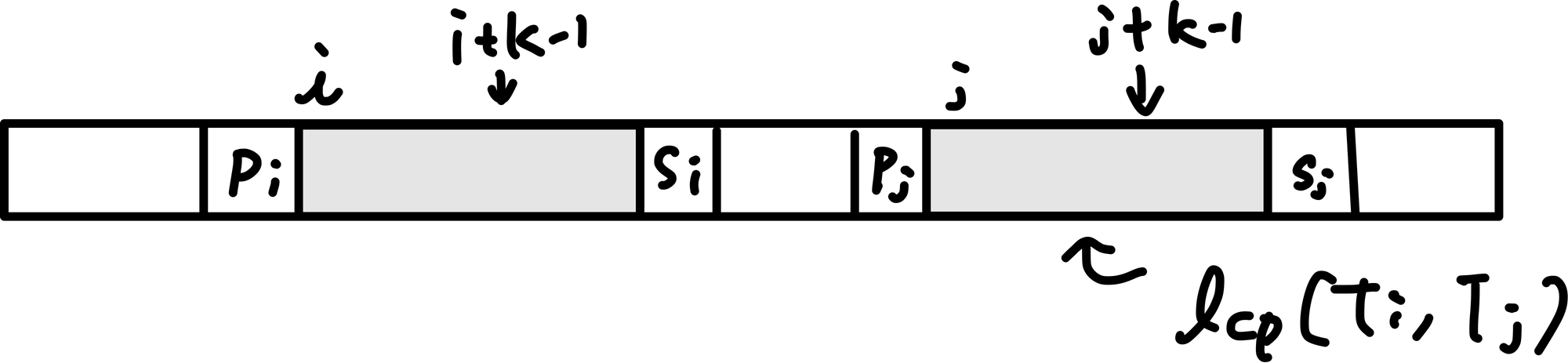
- $lcp(T_{i+1}, T_{j+1}) \geq lcp(T_i, T_j)-1$
- 先頭1文字削った文字列の$lcp$は削る前の$lcp-1$以上になる
- lcpの計算を一部省略できる！
- アルゴリズム
- $SA[i]=T_j$について、$rank[j]=i$となるようなランク配列を予め計算しておく
- $LCP[rank[i]]=lcp(T_i, T_{SA[rank[i]-1]})$の計算を$i=1$から順番に計算する
- これは$T_i$と辞書順が１つ前の（$SA$上で$T_i$と隣接する）suffix $T_{SA[rank[i]-1]}$との$lcp$を計算し、$LCP[rank[i]]$に保存している
- このとき、重要な性質を使って計算しなくても良い部分は計算しない
def lcp_kasai(T, SA):
n = len(T)
LCP = [0 for _ in range(n)]
rank = [0 for _ in range(n)]
for i, sa in enumerate(SA):
rank[sa] = i
l = 0
for i in range(n):
i1, i2 = i, SA[rank[i] - 1]
while i1 + l < n and i2 + l < n and T[i1 + l] == T[i2 + l]:
l += 1
LCP[rank[i]] = l
l = max(0, l - 1)
return LCP
- Kasaiアルゴリズムの計算時間は$O(n)$
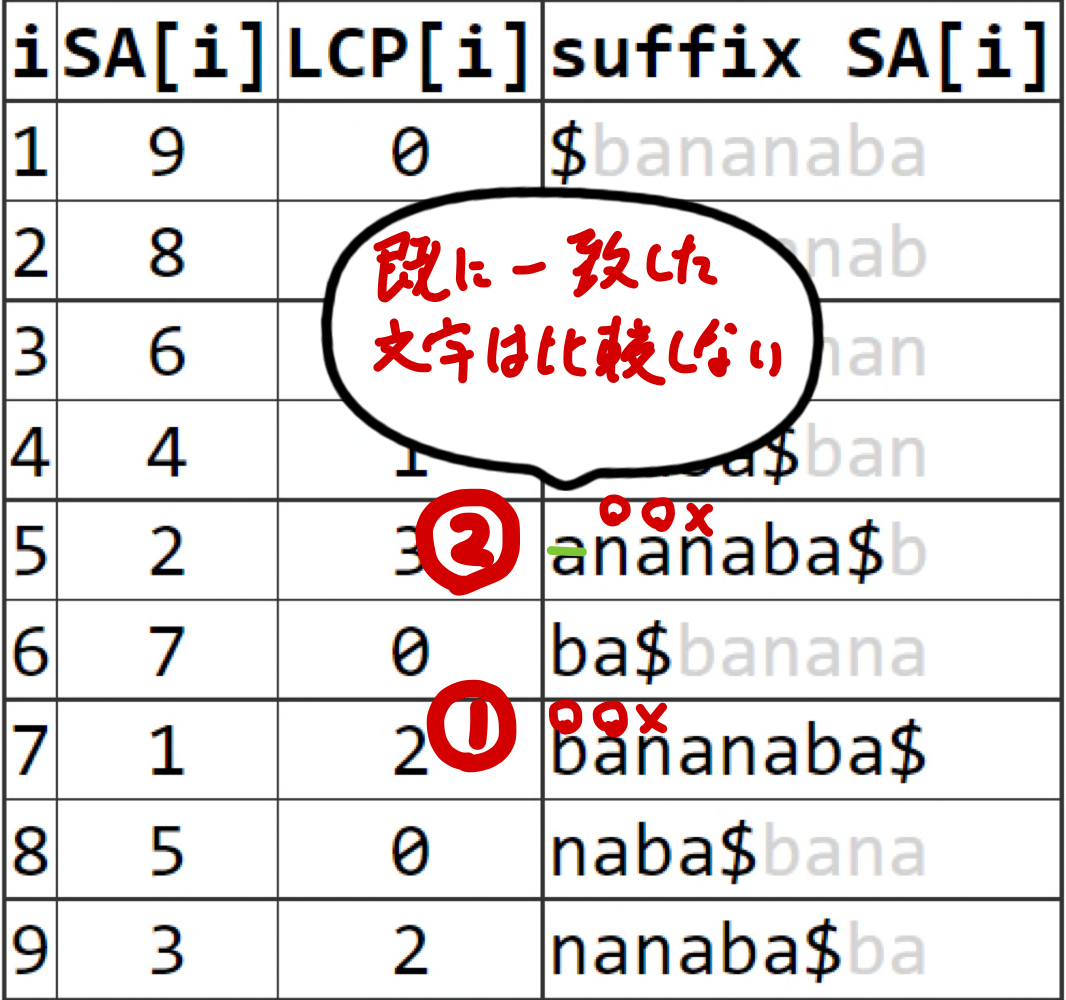
- アルゴリズムが比較する文字の数を数える
- アルゴリズムは$T$上でポインタ$i$をleft-to-rightにone-passで動かして$T[i]$が対応する文字と一致するかどうかを比較している点に注意
- 一致する数は全体で$n$回
- left-to-rightにone-passするだけ
- 一度一致した文字は二度と比較しない
- 不一致の数は全体で$n$回
- 不一致は$LCP[i]$の計算で1回しか起こらない
- アルゴリズムが比較する文字の数を数える
Permuted LCP Array
(Sadakane 2002, Khmelev 2004, Karkkainen+, 2009)
$$PLCP[i]=LCP[rank[i]]$$
- PLCP配列はLCP配列をランク順ではなくテキスト順に並べた配列
- PLCP配列はLCP配列の順列となる
- なぜPLCP配列を考えるのか？
- 簡潔に記述できる（たったの$2n$ bits！！）
- 整数配列として表現すると1要素あたり4バイト使用し全体で$4n$ bytes
- 簡潔な表現方法
- Kasaiアルゴリズムを走らせ、一致したときに1、不一致のとき0と記述する
- 1, 0の数はそれぞれ$n$個なので$2n$ bitsで表現できる
- $LCP[i]$が取り出せなくては困るのでは？
- PLCPの簡潔表現上でrank, selectデータ構造を構築すれば$LCP[i]=PLCP[SA[i]]$を$O(1)$で取り出すことができる
- LCP配列を計算するよりも（実用的に）高速にPLCP配列を計算することができる
- Kasaiアルゴリズムは$SA, rank, LCP$をランダムアクセスしキャッシュ効率が悪い
- SAから直接LCPを計算するよりSAからPLCPを経由してLCPを計算するほうが早い
- 簡潔に記述できる（たったの$2n$ bits！！）
KasaiアルゴリズムのPLCP計算 (Karkkainen+, 2009)
- （再掲）Kasaiアルゴリズムは$SA, rank, LCP$をランダムアクセスしキャッシュ効率が悪い
- $SA, rank, LCP$の3役をこなす$\Phi$を使ってキャッシュ効率を高める（ついでに領域も削減できる）
- ここで$\Phi[i]=SA[rank[i]-1]$
- $\Phi[i]$は$SA$上で$T_i$に隣接するsuffixのindexを指す
- （再掲 Kasaiアルゴリズム）$LCP[rank[i]]=lcp(T_i, T_{SA[rank[i]-1]})$の計算を$i=1$から順番に計算する
- $PLCP[i]=LCP[rank[i]]=lcp(T_i, T_{\Phi[i]})$
- この時点で1台2役
- Kasaiアルゴリズムで$\Phi$を使った$PLCP$の計算ができる
- さらに$\Phi[i]$は1回しか使われない
- $\Phi[i]$を使ったら、不要となった$\Phi[i]$に$PLCP[i]$の値を保存する
- 1台3役！！
- $PLCP[i]=LCP[rank[i]]=lcp(T_i, T_{\Phi[i]})$
def plcp_phi_inplace(T, SA):
n = len(T)
Phi = [0 for _ in range(n)]
for i in range(1, n):
Phi[SA[i]] = SA[i - 1]
l = 0
for i in range(n):
j = Phi[i]
while i + l < n and j + l < n and T[i + l] == T[j + l]:
l += 1
Phi[i] = l
l = max(0, l - 1)
return Phi
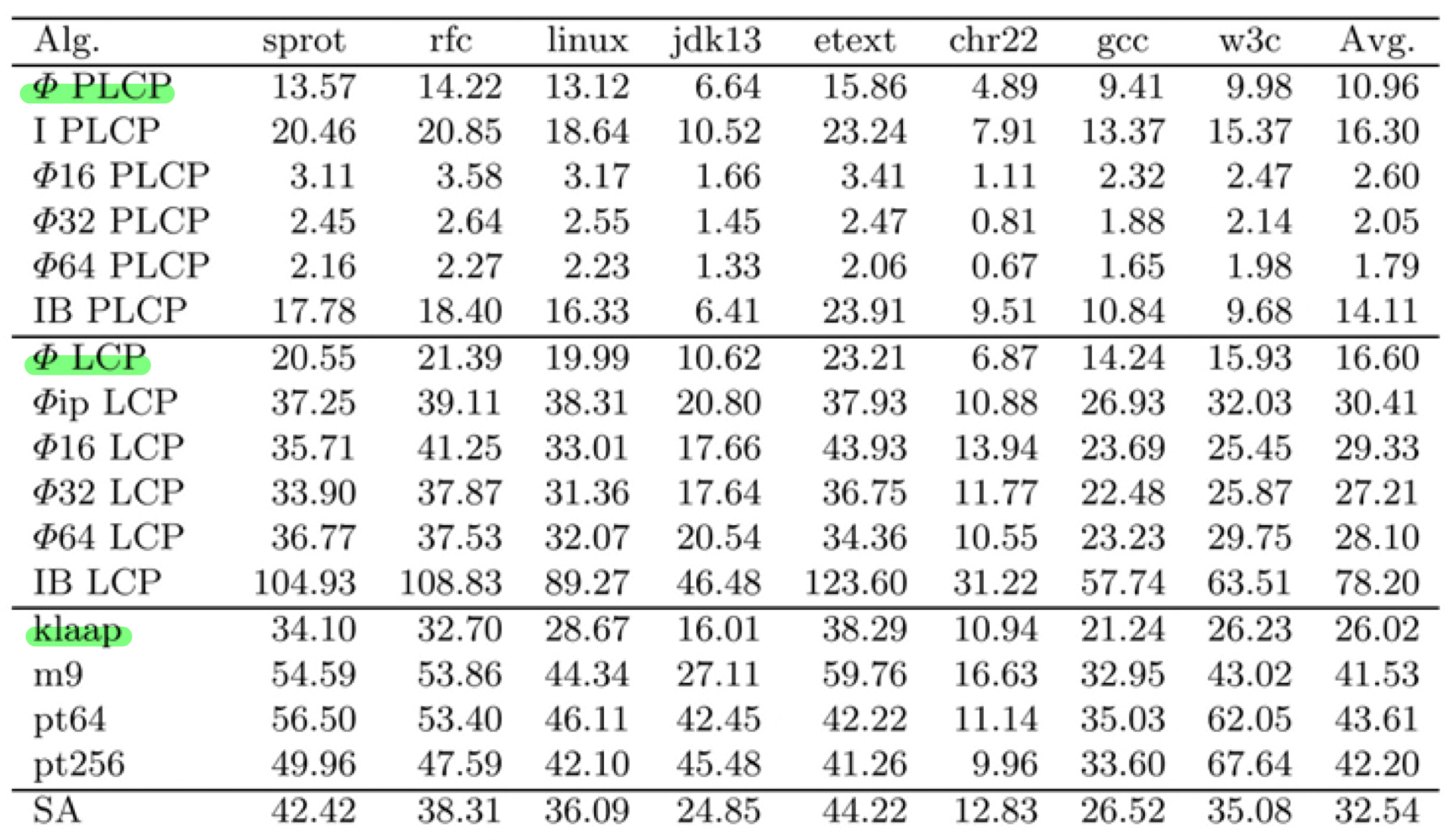
- 実行時間の比較 (Karkkainen+, 2009)
- PLCPの構築(ΦPLCP)はKasaiアルゴリズム(klaap)よりも約2倍高速
- PLCPを構築してからLCP配列を計算 (ΦLCP) してもKasaiアルゴリズムよりも高速
Irreducibleの性質を使ったPLCPの計算
(Khmelev 2004, Karkkainen+, 2009)
- 重要な性質
- $j = SA[rank[i]-1]$としたとき
- $T[i-1] = T[j-1]$ならば$PLCP[i]=PLCP[i-1]-1$となる
- このとき$PLCP[i]$をreducibleと呼ぶ（そうでない場合irreducibleと呼ぶ）
- $PLCP[i]$がreducibleで$PLCP[i-1]$の値が既知ならば$PLCP[i]$の計算を全て省略できる！
- なぜそうなるかというと、比較対象の文字列が同じで不一致箇所も同じになるので
- $T_i$と$T_j$は$SA$上で隣接し、$T_{i-1}$と$T_{j-1}$も必ず隣接する
- アルゴリズム
- Irreducibleな$PLCP[i]$のみをナイーブに計算する
- PLCP配列をleft-to-rightにone-passしてreducible LCPを計算する
def plcp_irreducible(T, SA):
n = len(T)
PLCP = [0 for _ in range(n)]
for i in range(n):
i1, i2 = SA[i], SA[i - 1]
if i1 == 0 or i2 == 0 or T[i1 - 1] != T[i2 - 1]:
l = 0
while i1 + l < n and i2 + l < n and T[i1 + l] == T[i2 + l]:
l += 1
PLCP[i1] = l
for i in range(1, n):
PLCP[i] = max(PLCP[i], PLCP[i - 1] - 1)
return PLCP
- PLCP構築の計算時間は$O(n+K)$ ここで$K$はirreducible lcpsの総和
- $K \in O(n^2)$が自明な上界だがもう少し良さそうに見える
（次の項目で示すように実際に高速）
- $K \in O(n^2)$が自明な上界だがもう少し良さそうに見える
Irreducible LCP予想 (Khmelev, 2004)
- 今回は定理 (Karkkainen+, 2009) の証明を説明する
定理 (Karkkainen+, 2009) の証明
- $PLCP[i]=lcp(T_i, T_j)$の$k$文字目、$T[i+k-1]$をカウントすることを考える
- ここで$j=\Phi[i]$
- カウント対象は上記のような$(i, k)$のペアの個数であることに注意（ここ大事）
- ただし上から抑えたいので数え方を工夫する
- $T$の逆文字列のSuffix Treeを考える
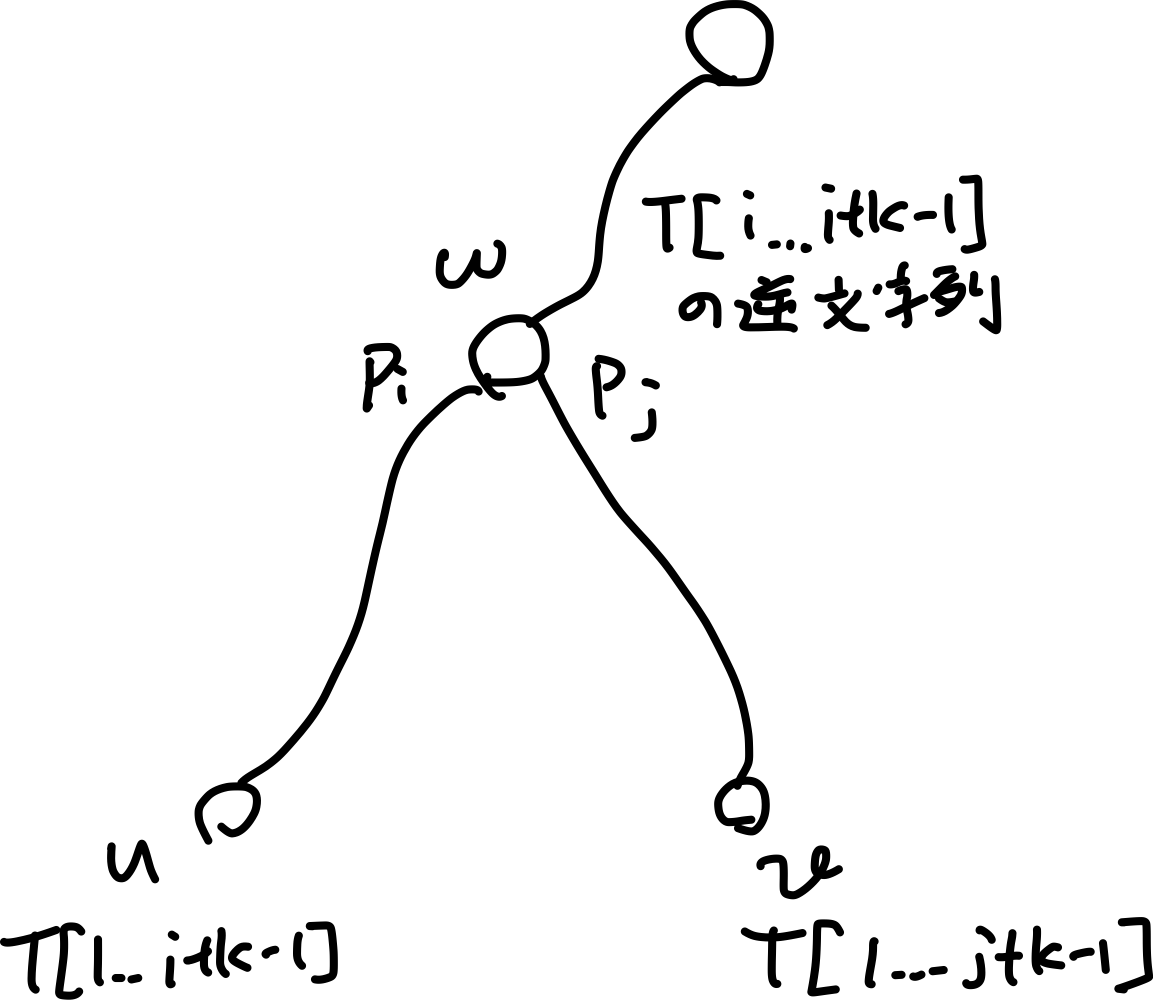
- $T[i..i+k-1]$を葉$u=T[1..i+k-1]$、$v=T[j..j+k-1]$を葉$T[1..j+k-1]$に対応付ける
- $u, v$のlowest common ancestorを$w=lca(u, v)$とする
- このとき$T_i$の$k$文字目$T[i+k-1]$をカウントするコスト1を
$w$の子供で$u$を含む部分木、$v$を含む部分木のうち小さい方の葉に割り当てる- これは$PLCP[i]=lcp(T_i, T_j)$の$k$文字目をカウントするときに、$(i, k)$としてカウントするべきところを、代わりに$(j, k)$としてカウントする（かもしれない）ことを意味している
- 何をしているかと言うと（繰り返しになるが）
数えやすいようにコストを分配している
- $u$にコストが割り当てられるとき
- $w$を$u$のcostly ancestor
- $v$を$u$のcostly cousinと呼ぶ
- $u$に割り当てられる最大コストを見積もりたければ、対応するcostly ancestor $w$とcostly cousin $v$の最大数を見積もれば良い
-
補題：1つの葉に割り当てられるコストは高々$2 \log n$
-
これが成り立つならトータルのコストは高々$2n \log n$となり定理が成り立つ
-
補題：$u$は高々$\log n$個のcostly ancestorを持つ
- $w$の部分木サイズは$u$を含む$w$の子供の部分木のサイズの2倍以上となる
- つまり$u$のcostly ancestorをサイズ順に並べると倍々になっていく
- よって$u$のcostly ancestorは高々$\log n$個しか存在しない
-
補題：$u, w$を固定したとき、$u$は高々2個のcostly cousinを持つ
- $u$, $w$を固定すると$u$に対応するsuffix $T_i$とカウント対象の文字$T[i+k-1]$がユニークに対応する
- なぜか？
- $u$は逆文字列のsuffix treeの葉なのでprefix $T[1..x]$に対応する
- $w$はカウント対象のsuffixの$k$文字目までのprefixに対応する
- $u$はsuffix $T_i=T_{x-k+1}$に対応する
- $T_i$の$k$文字目としてカウントされるのは
$PLCP[i]=lcp(T_i, T_j)$と$PLCP[j]=lcp(T_j,T_i)$の高々2通りしかない- ここで$j$は$j=\Phi[i]$もしくは$i=\Phi[j]$
- $SA$上で$T_i$に隣接するsuffixは2通り
- なぜか？
- $u$, $w$を固定すると$u$に対応するsuffix $T_i$とカウント対象の文字$T[i+k-1]$がユニークに対応する
-
よって**葉に割り当てられるコストは高々$2 \log n$**となる
-