LLM用のデータセットをLLMで作成・評価
前回の記事に続き、松尾研LLM開発コンペ2025での評価についての記事となります。
※ コンペ内で評価を担当したわけではありませんが、1部評価を回したり、評価スコアについて他の方から聞いたor自身でデータを見た結果、考察した点などを記載します。
本選への参戦
残念ながら、予選のCogitoチームではスコアが大幅に下がるという現象が発生し、本選では、別のチームとして参加という状態になりました。
Pont Neufを選んだ理由
予選ではDeepSeek-R1モデルを使用していたため、別のモデルも見てみたいという気持ちがあり、Qwen235Bを提出したPont Neuf又は、RAMENチームへの応募を考えました。次に、RAMENチームが MISOラーメン だったこともあり、豚骨ラーメン派だった私はPont Neufチームへの応募を実施しました。※ SIOラーメン のモデルもあったようです。
(ただし、最終的には全チームQwen235Bベースにて提出との事)
- 予選でPontNeufチームがQwenモデルを使用していた
- 私が、豚骨ラーメン派だった
- 過去にフランス語を勉強し、自分でもろもろ手配してフランス旅行した事があった
以上の観点から、Pont Neufチームへの応募を決意致しました。
本選は予選よりも短い期間であり、すでに進んでいるチームに参加させて頂いて何か貢献できるのか?という不安はかなり有りましたが、ミーティング動画などを逐一記録・公開していてくれたりなどで、かなりキャッチアップがやりやすかったと感じました。
LLMでのデータ合成・評価
いわゆるsynthetic dataと呼ばれるLLMで、LLM用のデータセットをLLMで作成する手法があります。
メリットとしては、(GPU資産さえあれば)人件費を限りなく抑えてデータを大量に用意する事ができる点があります。
また、合成と同じく、LLMでLLMを評価するLLM-as-a-judgeという手法もあります。本コンペでは、はそのような評価手法が採用されていました。
また、本コンペにおける運営から提供されたデフォルトコードの場合、Qwen/Qwen3-32Bにて、HLEのスコアを出すという形になっており、最終的なスコア判定はOpenAIのGPTを使用して判定という形式でした。
使用可能なモデルの内、各チームで評価に使うモデルもその中から選出し、各自が提供リソースでの手元評価を実施しておりました。
LLM評価であれば、人によるバイアスや評価のブレなどを防ぐことができますが、人手とは違ったLLMによるバイアスが存在し、LLM-as-a-judgeの論文内でも言及されています。
LLM as a Judge
LLMの回答を評価する
GPT-3の頃であれば、出力を人間が評価する場合、明らかに間違っている事が簡易に判別できておりました。しかし、昨今のLLM性能の向上による高難易度な内容や、膨大な長文を人手で評価することは凄く困難です。
特に、長文の場合、
- 最初は正しいが、途中からおかしいもの。
- 基礎知識は合っているが、その後の解説だけ違うもの。
- ところどころおかしいが、結論は合っているもの。
- 最初と結論もあっているが、途中の文章がおかしいもの。
等々、これらすべてを人手で同じ判断基準を設け、どちらがいいか、何点かなどをスコア付けする事が非常に困難になってきております。
であるからこそ、高品質な学習データを得るため、高い報酬を払ってデータセット作成の求人などが出ているのでしょう。
LLMのバイアス
- 自己強化バイアス:自分自身が生成した応答を好む
- 位置バイアス:特定の順番や位置にある応答をひいきにする
- コンバッション・フェード・バイアス:モデル名が明示されている場合に発生する(gpt-4)
- 長さバイアス:より冗長な応答を好む傾向
- 具体性バイアス:具体的な詳細を含む応答を好む
今回のコンペでも、学習したモデルの出力をよく見てなかった場合、本当に性能が向上しているかの判断を誤る事になった気がしております。
LLM-as-a-judgeにおける注意点
- LLM-as-a-judgeの評価結果を過信しすぎない。
→ 指標・指針の一つとする - 実際に使用する場合は、評価結果に問題がないかを確認する。
- 特に信頼性が求められる評価の場合には全件を確認する。
→ 人間による評価の補助としてLLM-as-a-judgeを導入する。
[*1] https://www.youtube.com/watch?v=QML5Qu0PZ6M (引用
「LLM-as-a-Judge: 文章をLLMで評価する」中山 功太 国立情報学研究所大規模言語モデル研究開発センター・特任研究員
本コンペでの敗因分析
以下、HLEの問題自体が難しい+膨大である、Gemini君に手伝ってもらいながら、さくっと敗因分析などを考えてもらいました。
予選
全問題数2,500件のうち、2158問(Text only)を対象に実施されました。
【予選結果発表会より】
また、部分点評価はanswer + rationale をGPT-o4-miniにて評価されました。
不正解の理由
予選で「推論のどの段階で失敗したか」という観点で分類を試みるため、不正解となった問題の内TF-IDFを使い、judgementからキーワードを抜き出します。
judgement : 提出したチームの回答と、正解の間に意味のある違いがあるかどうかのみに焦点を当てたLLM(GPT-o4-mini)による説明です。
# df_resultsは、評価コードから得られた結果のhle_hle_results.jsonlを
# pandasに読み込ませたデータです。
# 不正解データのみを抽出
df_incorrect = df_results[df_results['correct'] == 0].copy()
# TF-IDFを用いてキーワードを抽出
from sklearn.feature_extraction.text import TfidfVectorizer
# TF-IDFの準備(英語の一般的な単語は除外)
vectorizer = TfidfVectorizer(stop_words='english', max_features=50)
# judgementテキストにTF-IDFを適用
try:
tfidf_matrix = vectorizer.fit_transform(df_incorrect['judgement'].fillna(''))
feature_names = vectorizer.get_feature_names_out()
# 各単語の重要度(TF-IDFスコアの合計)を計算
scores = tfidf_matrix.sum(axis=0).A1
word_scores = sorted(list(zip(feature_names, scores)), key=lambda x: x[1], reverse=True)
print("\n--- TF-IDFによって抽出された重要キーワード Top 30 ---")
print([word for word, score in word_scores[:30]])
except Exception as e:
print(f"\nTF-IDFの実行中にエラーが発生しました: {e}")
print("judgementに有効なテキストデータが少ない可能性があります。")
feature_names = [] # エラー時は空リストにする
--- TF-IDFによって抽出された重要キーワード Top 30 ---
['rationale', 'reasoning', 'model', 'key', 'execution', '10', 'self', 'method', 'correctly', 'correct', 'understanding', 'monitoring', 'fails', 'checkpoints', 'idea', 'shows', 'minimal', 'incorrect', 'core', 'overall', 'steps', 'irrelevant', 'restates', 'credit', '20', 'approach', 'checks', 'identifies', 'problem', 'valid']
上記のような結果が得られたため、大まかに分類してみます。
def classify_error_by_process(judgement):
""" 推論プロセスに着目してエラーを分類する関数 """
s = str(judgement).lower()
# 複数のキーワードを組み合わせて、より具体的なエラーを先に判定する
# 1. 問題の誤解
if ('understanding' in s and 'incorrect' in s) or 'misunderstands' in s or 'misinterprets the problem' in s:
return '問題の誤解'
# 2. 実行/計算の誤り (アプローチは良いが実行で失敗)
# "correct reasoning but incorrect execution" のようなパターンを想定
if ('execution' in s) and ('fails' in s or 'incorrect' in s or 'error' in s):
# reasoningがcorrectであると言及されていれば、より確度が高い
if 'correct reasoning' in s or 'valid approach' in s:
return '実行/計算の誤り (アプローチは正解)'
return '実行/計算の誤り'
# 3. アプローチ/推論の誤り
if ('reasoning' in s or 'rationale' in s or 'approach' in s or 'steps' in s or 'method' in s) and \
('incorrect' in s or 'fails' in s or 'flawed' in s or 'wrong' in s):
return 'アプローチ/推論の誤り'
# 4. 無関係/不十分な回答
if 'irrelevant' in s or 'restates the problem' in s:
return '無関係な回答'
if 'incomplete' in s or 'misses' in s:
return '不十分な回答'
# 5. 上記に当てはまらない一般的な不正解
if 'incorrect' in s or 'not correct' in s:
return '不正解(一般的)'
return 'その他'
# 不正解データに新しい分類を適用
df_incorrect = df_results[df_results['correct'] == 0].copy()
df_incorrect['error_type_process'] = df_incorrect['judgement'].apply(classify_error_by_process)
# 新しい分類で集計
error_summary_process = df_incorrect.groupby(['phase', 'team', 'error_type_process']).size().unstack(fill_value=0)
# 予選の結果を可視化
if 1 in error_summary_process.index.get_level_values('phase'):
ax = error_summary_process.loc[1].plot(
kind='bar',
stacked=True,
figsize=(14, 7),
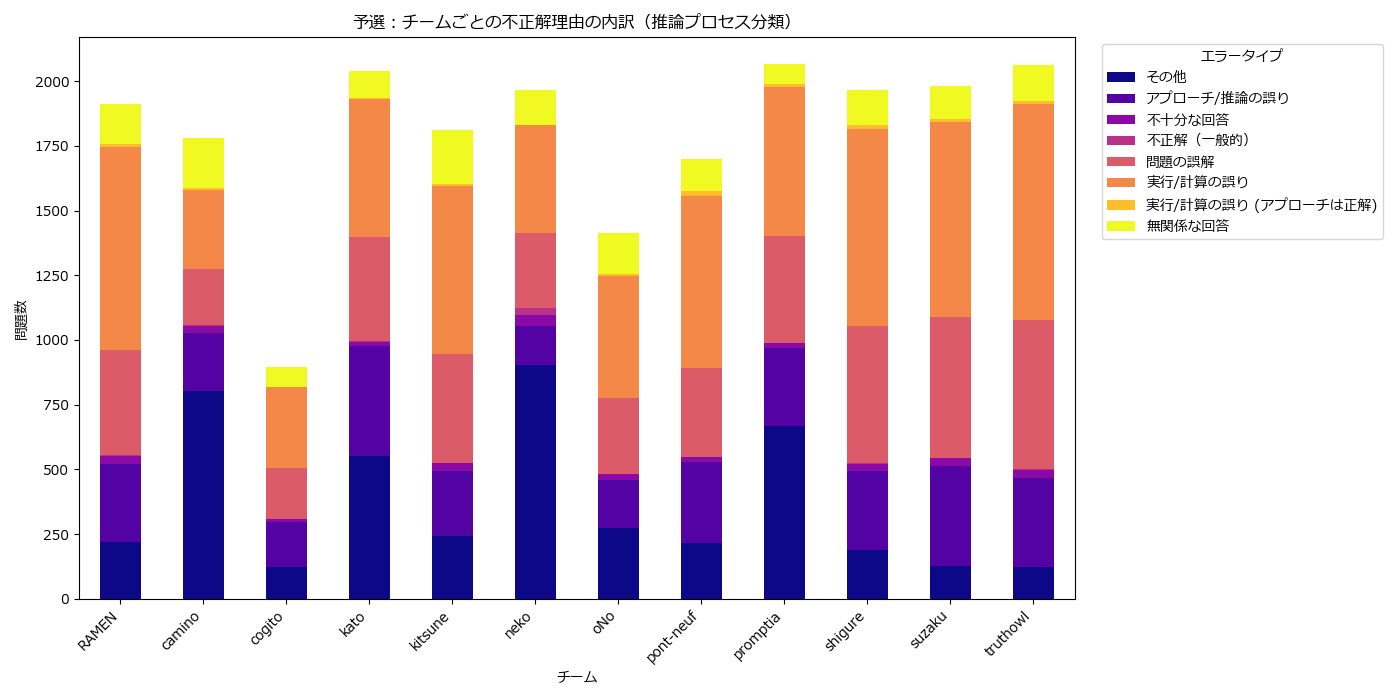
title='予選:チームごとの不正解理由の内訳(推論プロセス分類)',
cmap='plasma' # 別のカラーマップを試す
)
plt.ylabel('問題数')
plt.xlabel('チーム')
plt.xticks(rotation=45, ha='right')
handles, labels = ax.get_legend_handles_labels()
plt.legend(reversed(handles),reversed(labels),title='エラータイプ', bbox_to_anchor=(1.02, 1), loc='upper left')
plt.tight_layout()
plt.show()
全チームに共通して言えるのは、「実行/計算の誤り」が主要な不正解元となっています。そのうち、アプローチは正しいが最終的な計算・整形で誤りというパターンが多いように感じられました。
また、
- 「アプローチ/推論の誤り」の数に比べて「実行/計算の誤り」の数が多いチームは、正しい方針を立てる能力は高いものの、詰めの甘さで失点している傾向がある
- 「実行/計算の誤り」に対する「アプローチ/推論の誤り」や「問題の誤解」の割合が比較的高いチームは、最終的な計算以前に、問題の解き方そのものや、問題文の解釈でつまずいているケースが多い可能性
- 「その他」の割合が突出して高いチームは、定義したエラーパターンに当てはまらない、ユニークなあるいは予測不能な間違い方をしている可能性を示唆しており、モデルの挙動が不安定である可能性
との事でした(Gemini君)
LLM-as-a-judgeもCoTをして評価の精度を上げる方法もあるようなので、上記のような不正解理由を分けて取り出すような処理を実施すれば、さらなる敗因分析によって次の戦略が立てられそうな気がします。
Multipul問題における解答形式
次に、選択式問題におけるLLM-as-a-judgeの気になる部分を見てみました。
LLM-as-a-judgeの根本的な間違いのケース
問題id: 669402b41dcb3d5a1ef9e951
正式な解答はZ+Z+Z+Z+Zだが、
Z^5 と回答したチームが正解となっていた。
問題id:66e942c180435ab1cb1ef049
正解 $TC^0$
上付きの0が正解だが、上付きでない【TC0】も正解としている。
こういった問題を抽出していくことで、どのようにLLM-as-a-judgeを改善していけばの改善戦略のタネになるかもしれません。
小学校などのテストだったら×又は△にされそうな問題
問題id: 66f378a504165ae3e4f46de9
Answer Choices: A. 1 B. 2 C. 3 D. 4 E. 5 F. 6という問題の場合
【A】,【 A. 1】ともに正解判定
というケースがあったため、シンプルに答えた場合と、選択肢文章まで一緒に答えた場合の正答率を算出しました。
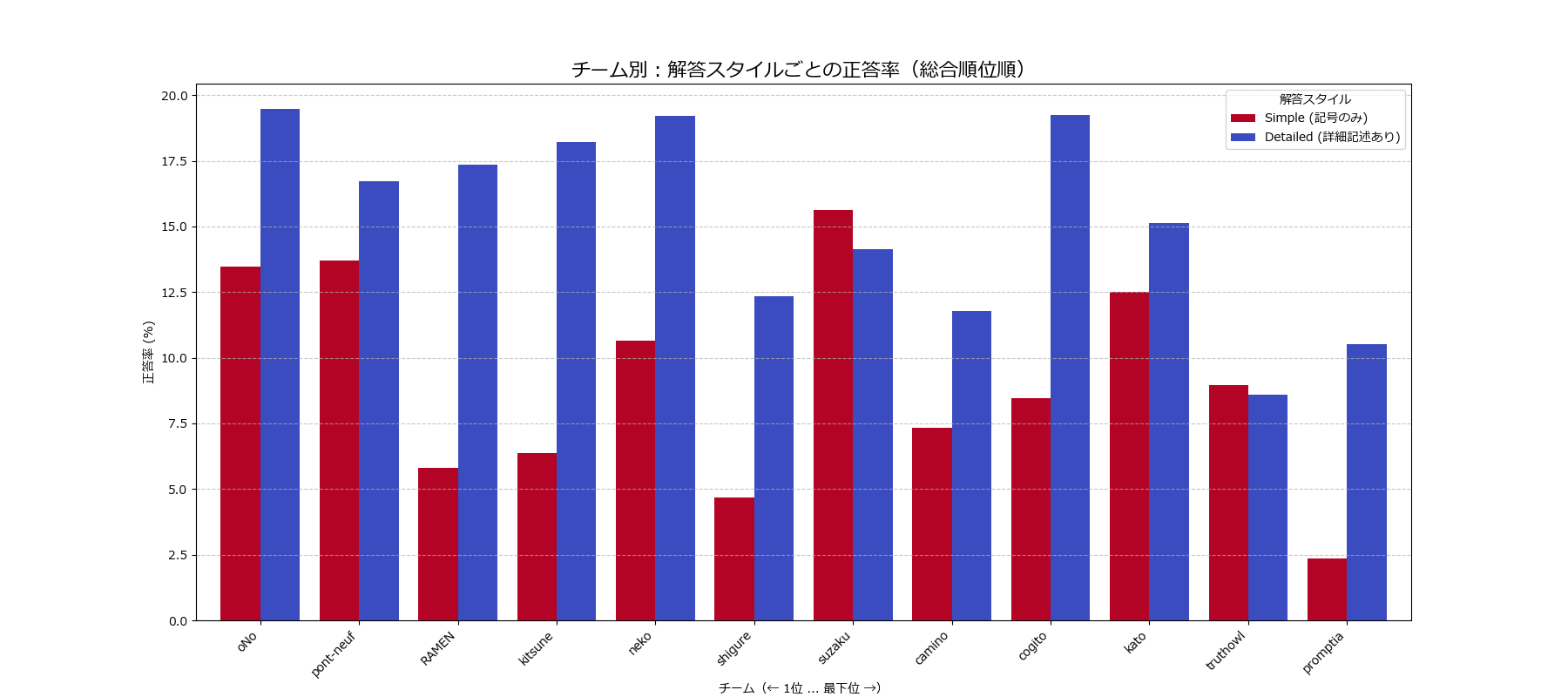
問題内容によると思いますが、【A】とだけ答えた問題より、【A : MATSUO】という形で選択肢文章も与えている方が正答率が高くなる。という事が多数のチームで見られました。
【思考が間違っているが答えは合っている。ではなく、思考が正しく解答を導く能力が高いため、根拠となる文言が一緒に出てきている?】
その原因を探るため、各モデルの回答を見てみようとしましたが、問題文自体が難しすぎて時間がかかりすぎるため、本記事では断念しました。。
本選
本選では、3チームともスコア向上を実現できておりました。
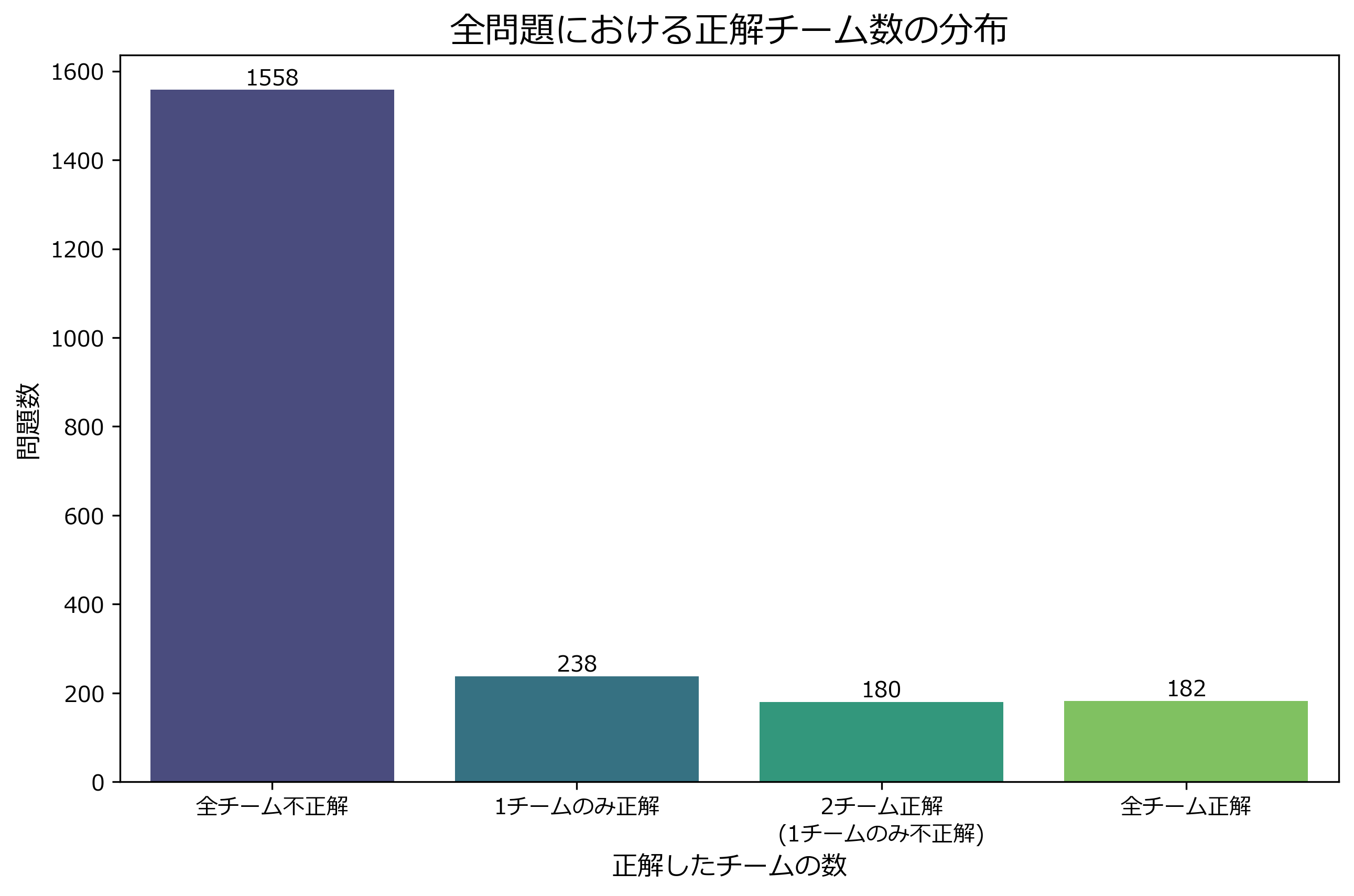
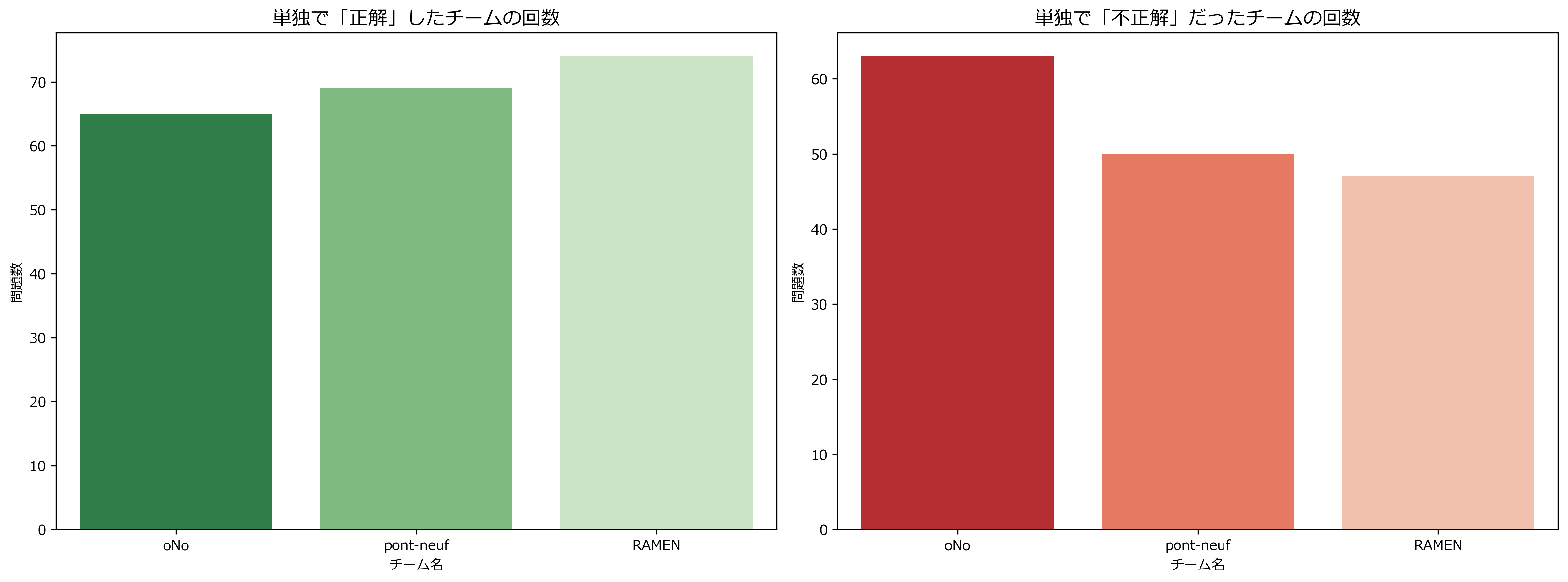
以下は、本選において、勝負の分かれた問題件数です。
※ RAMEN, pont-neufチームが2157件解答を出したのに対し、oNoチームは1971件の出力でした。(謎)
3チーム毎の正解数
そのうち、【1チームのみ正解した数】が多いRAMENチームの優勝となりました。
本選での不正解理由
予選と同じく、本選でもエラータイプによる分析をしてみます。
# --- 準備:本選データのみを抽出 ---
df_incorrect_p2 = df_incorrect[df_incorrect['phase'] == 2].copy()
error_summary_p2 = error_summary_process.loc[2]
# --- エラー数の合計を計算し、各エラータイプの割合(%)を算出 ---
error_ratio_p2 = error_summary_p2.div(error_summary_p2.sum(axis=1), axis=0) * 100
# --- グラフ化 ---
ax = error_ratio_p2.plot(
kind='bar',
stacked=True,
figsize=(12, 8),
cmap='plasma',
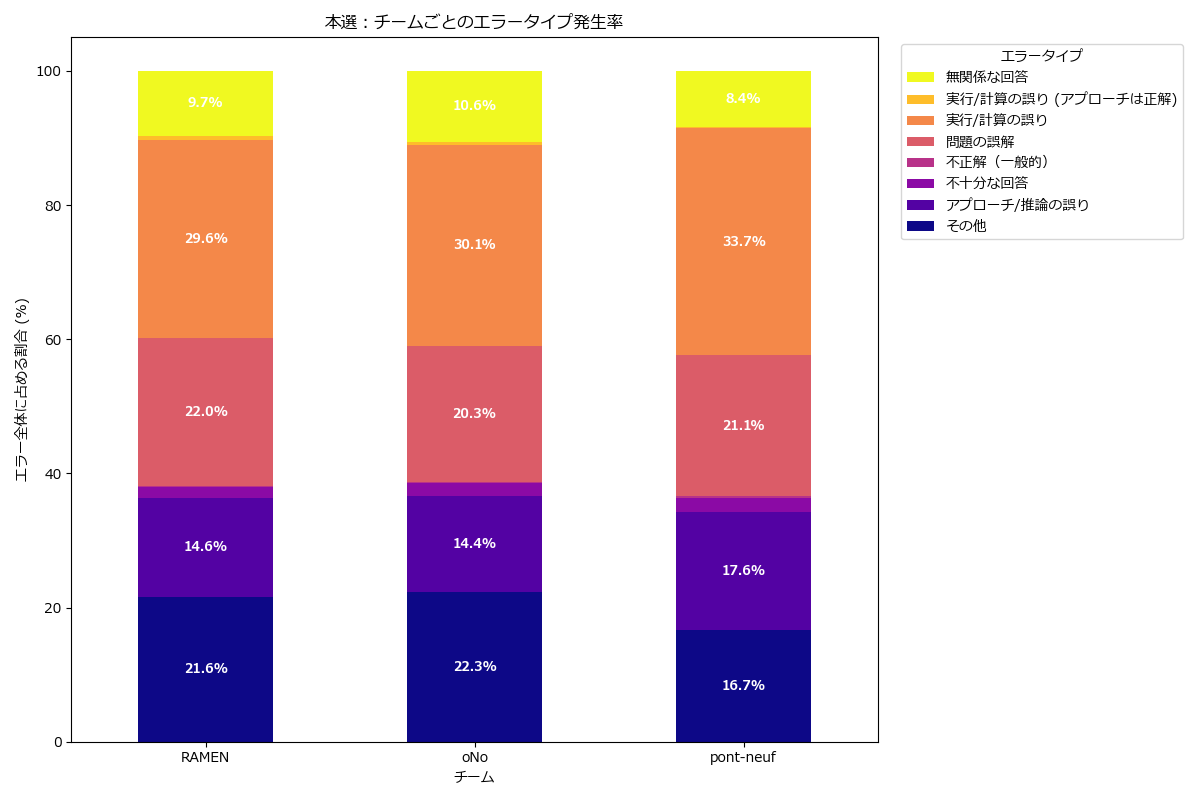
title='本選:チームごとのエラータイプ発生率'
)
# グラフの装飾
plt.ylabel('エラー全体に占める割合 (%)')
plt.xlabel('チーム')
plt.xticks(rotation=0)
handles, labels = ax.get_legend_handles_labels()
plt.legend(reversed(handles),reversed(labels),title='エラータイプ', bbox_to_anchor=(1.02, 1), loc='upper left')
plt.tight_layout()
# 積み上げグラフの各セグメントに割合を表示
for container in ax.containers:
# 小さすぎる値はラベル付けしない
labels = [f'{v.get_height():.1f}%' if v.get_height() > 3 else '' for v in container]
ax.bar_label(container, labels=labels, label_type='center', color='white', fontsize=9, fontweight='bold')
plt.show()
# --- 数値データも表示 ---
print("--- 本選:チームごとのエラータイプ発生率 (%) ---")
display(error_ratio_p2)
--- 本選:チームごとのエラータイプ発生率 (%) ---
| error_type_process | その他 | アプローチ/推論の誤り | 不十分な回答 | 不正解(一般的) | 問題の誤解 | 実行/計算の誤り | 実行/計算の誤り (アプローチは正解) | 無関係な回答 |
|---|---|---|---|---|---|---|---|---|
| RAMEN | 21.640091 | 14.635535 | 1.708428 | 0.170843 | 22.038724 | 29.555809 | 0.569476 | 9.681093 |
| oNo | 22.311002 | 14.382299 | 1.905347 | 0.061463 | 20.282729 | 30.055317 | 0.430240 | 10.571604 |
| pont-neuf | 16.666667 | 17.633675 | 2.047782 | 0.227531 | 21.103527 | 33.731513 | 0.227531 | 8.361775 |
そこまで大きな差は見られなかったので、
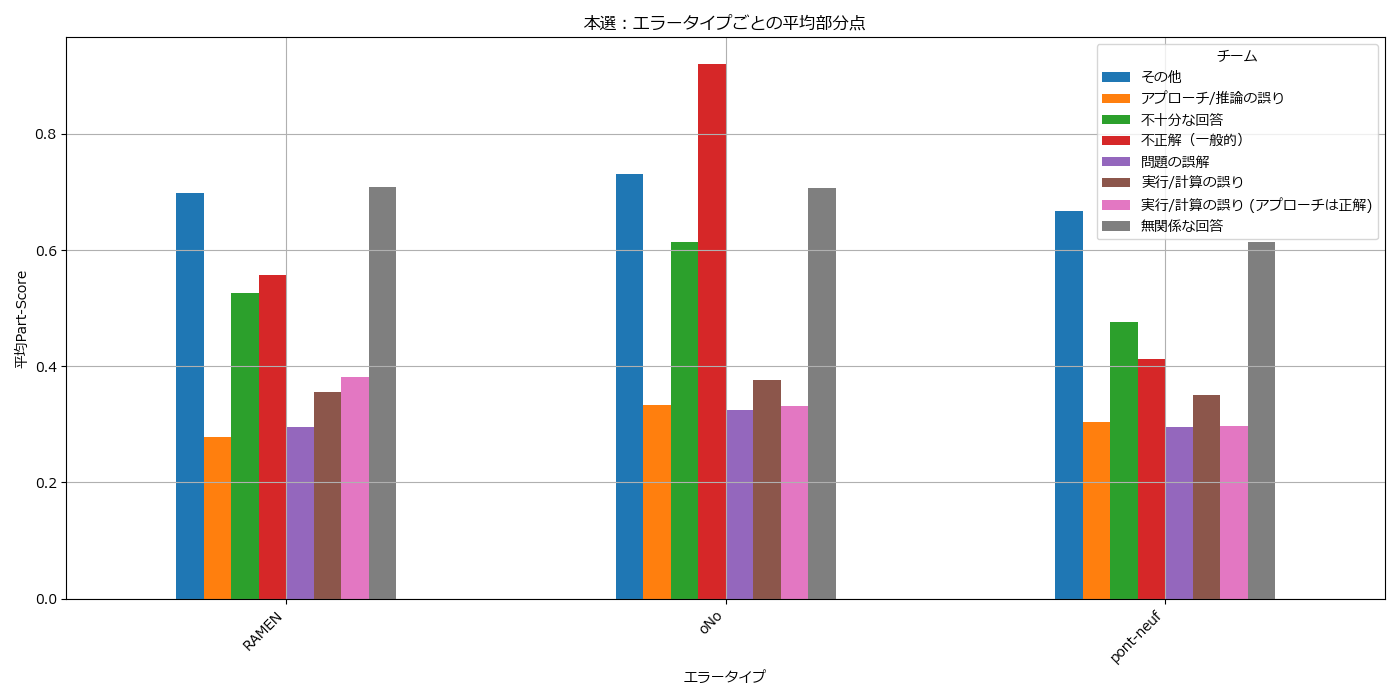
次は、part-scoreを使用した、平均部分点を見てみます。
# --- エラータイプごとの平均部分点を算出 ---
avg_part_score_by_error = df_incorrect_p2.groupby(['team', 'error_type_process'])['part-score'].mean().unstack()
# --- グラフ化 ---
avg_part_score_by_error.plot(
kind='bar',
figsize=(14, 7),
title='本選:エラータイプごとの平均部分点',
grid=True
)
plt.ylabel('平均Part-Score')
plt.xlabel('エラータイプ')
plt.xticks(rotation=45, ha='right')
plt.legend(title='チーム')
plt.tight_layout()
plt.show()
# --- 数値データも表示 ---
print("\n--- 本選:エラータイプごとの平均部分点 ---")
display(avg_part_score_by_error)
--- 本選:エラータイプごとの平均部分点 ---
| error_type_process | その他 | アプローチ/推論の誤り | 不十分な回答 | 不正解(一般的) | 問題の誤解 | 実行/計算の誤り | 実行/計算の誤り (アプローチは正解) | 無関係な回答 |
|---|---|---|---|---|---|---|---|---|
| RAMEN | 0.698026 | 0.277665 | 0.525667 | 0.556667 | 0.294625 | 0.355048 | 0.382000 | 0.709294 |
| oNo | 0.730275 | 0.333932 | 0.614516 | 0.920000 | 0.325545 | 0.375971 | 0.331429 | 0.706860 |
| pont-neuf | 0.667952 | 0.303871 | 0.475556 | 0.412500 | 0.294960 | 0.350202 | 0.297500 | 0.613810 |
【※ 以下、Gemini君の考察(まるなげ式)】
分析1: エラー発生率の再評価
まず、エラー発生率の数値データを詳しく見ていきましょう。
| チーム | 実行/計算の誤り (合計) | 根本的な誤り (合計) |
|---|---|---|
| RAMEN | 30.1% | 36.7% |
| oNo | 30.5% | 34.7% |
| pont-neuf | 34.0% | 38.7% |
※「実行/計算の誤り(合計)」 = 実行/計算の誤り + 実行/計算の誤り (アプローチは正解)
※「根本的な誤り(合計)」 = アプローチ/推論の誤り + 問題の誤解
-
pont-neufの課題がより明確に:
-
pont-neufは**「実行/計算の誤り」の合計が34.0%と、他の2チームより約4ポイント高い**ことがわかります。これは、やはり最終段階でのミスが失点の主要因であったことを強く裏付けています - 一方で、「根本的な誤り(アプローチ+問題誤解)」の合計は38.7%と3チームの中で最も高いですが、これは不正解数が多かったためで、個々の割合で見るとoNoよりは低い傾向にあります
-
-
RAMEN vs oNo の比較:
-
RAMENとoNoは、「実行/計算の誤り」の合計率がほぼ同じ(約30%)です。これは非常に興味深い点で、両者の違いは「計算精度」そのものではなく、「どのような問題で計算ミスをしたか」、あるいは「計算以外の部分での差」にある可能性を示唆しています -
oNoはRAMENに比べて「問題の誤解」の割合がわずかに低く、「アプローチ/推論の誤り」も同程度です。一見するとoNoの方が推論能力が高そうに見えますが、次の部分点の分析で評価が逆転します
-
分析2: 平均部分点の深掘り
次に、平均部分点の数値データを詳しく見ます。これは「間違いの質」を評価する上で最も重要な指標です。
-
oNoの「見当違いなエラー」:
-
oNoは「アプローチ/推論の誤り」で0.334、「問題の誤解」で0.326と、他の2チームに比べて明らかに高い部分点を獲得しています -
しかし、これは先ほどの考察とは逆の結果に見えます。なぜでしょうか?
-
仮説1:
oNoのモデルは、間違った方向に進んでも、その間違った理屈の中では非常に説得力のある、もっともらしい回答を生成する能力が高いのかもしれません。採点モデルがその「もっともらしさ」を評価して、結果的に部分点が高く出ている可能性があります -
仮説2:
oNoは、簡単な問題での「根本的な誤り」が多く、それらは少しの部分点をもらいやすいため、平均点が引き上げられている可能性も考えられます
-
仮説1:
-
-
pont-neufの堅実さの裏付け:
-
pont-neufは、先ほどの考察では「粘り強い」と評価しましたが、数値を見ると多くのカテゴリで最も平均部分点が低いという結果になっています。特に「アプローチ/推論の誤り(0.304)」や「実行/計算の誤り(0.350)」で顕著です -
この矛盾をどう解釈するか?
- これは、
pont-neufが**「0点か、高得点か」というような極端な間違い方をせず、常にそこそこの部分点を稼ぐ安定性**を意味しているのかもしれません。グラフでは平均値のバーが低く見えても、0点に近いような大失敗が少ないため、結果として総合スコアが安定していた可能性があります
- これは、
-
-
RAMENの質の高いアウトプット:
-
RAMENは、「実行/計算の誤り」での平均部分点が0.355と、pont-neufとほぼ同等で、oNoよりは低いです - しかし、特筆すべきは**「無関係な回答」の平均部分点が0.709と非常に高い**点です。これは、一見無関係に見える回答でも、問題に関連する有用な情報や正しい知識の断片が含まれていることが多かったことを示唆しています。モデルの基礎的な知識量が豊富であることの現れかもしれません
-
総合的な考察のアップデート
これらの数値データを踏まえて、各チームのモデル像をより解像度高く修正します。
-
RAMEN: 「知識豊富で、実行精度が高い優等生」
- 予選からの改善で得た高い実行精度が強み
- 一見的外れに見える回答(無関係な回答)でさえも、基礎知識に裏打ちされた質の高さが伺える
- 一方で、「その他」に分類されるような複雑なエラーや、根本的な推論の部分ではまだ改善の余地を残している
-
oNo: 「発想は豊かだが、時に暴走するトリックスター」
- 間違った方向に進んでも、その道筋の中では一貫性のある「もっともらしい」回答を生成する能力に長けている。これが高い部分点に繋がっている可能性がある
- しかし、その「もっともらしさ」が逆に仇となり、根本的な間違いに気づかず突き進んでしまう危うさも抱えている。スコアのばらつきが大きいモデルかもしれない
-
pont-neuf: 「大崩れしない、安定志向の堅実派」
- 最大の課題は、方針が立った後の最終的な実行精度。ここで失点を重ねてしまった
- 大きな失敗をしない安定性はあるものの、部分点の平均が全体的に低いことから、突出して評価されるような「輝きのある間違い(惜しい間違い)」も少なかった可能性がある。堅実さが、逆にスコアを伸ばしきれない原因になったとも考えられる
【Gemini君の考察】
このような分析もパパっとやってしまうLLMは凄いですね。。。
補足 : コンテキスト長によるスコア変動
2025/10/13に東京大学にて、結果発表がありましたが、その際、評価するためのコンテキスト長によってもスコアが変動するという事が伝えられました。
Onoチームだけコンテキスト長が短い設定になっていたことも有り、同じ設定になった場合、結果がどうなっていたかは気になるところでした。
おわりに
本来はLLM-as-a-judgeで評価モデルによるスコアの違いが出るかを実施して考察したかったのですが、個人のローカルLLMだとあまりにも時間がかかりすぎて終わらない。という事もあり、本記事では断念しました。
ただし、あくまで今回でのLLM-as-a-judge(HLEのGithubコード)は、正解と抽出した返答が正しいかを判定するだけに使われているため、そこまで大きい変動が生じることはないんじゃないかと感じております。
松尾研コミュニティーでは、このように無料でLLMなどに関する事が生べるためお勧めです!まだ参加されていない方がいれば是非
https://matsuolab-community.connpass.com/
プロジェクトのクレジット
本プロジェクトは、国立研究開発法人新エネルギー・産業技術総合開発機構(以下「NEDO」)の「日本語版医療特化型LLMの社会実装に向けた安全性検証・実証」における基盤モデルの開発プロジェクトの一環として行われます。