はじめに
最近、不均衡データを扱うことがあり、その対処方法を少し勉強しました。
不均衡データとは、正例と負例の比率が 「0.01:0.99」のような比率の偏った学習データのこと言います。
これほどの偏ったデータの場合、全てのデータを「負例」と予測すれば正答率(Accuracy)は**99%**となります。
精度だけみると、素晴らしい分類器のように見えます。
しかし、混合行列で見ると問題は一目瞭然です。
| Positive | Negative | |
|---|---|---|
| True | 0 | 10 |
| False | 0 | 990 |
| ※正例が10件、負例が990件のデータ |
この分類器は**正例データを1件も正例と予測していません。**つまり、感度(正例を正しく正例と判定する確率)は「0%」です。
疾患の有無を判別する検査の例で考えた場合、正答率を高めるために「ほとんどの人は疾患がないので、みんな疾患なし」と判別しているようなものです。もはや、検査の意味がないですね。。
何も工夫しない場合、上記のような問題が起こる可能性が高くなります。
主な対処手法としては、
- データ数の調整(オーバーサンプリング・アンダーサンプリング等)
- 学習時にクラスの重みを調整
に大別されるようです。
両方とも対処方法としては直感的であり理にかなっていると思いました。
詳しいことはこちらのSlideShareに分かりやすく書いていました。
不均衡データのクラス分類
今回は、「学習時のクラスの重みを調整」について簡単な実験をしてみました。
重みの調整
誤差関数にクラスの重みを加えて、正例を負例と誤分類した場合のペナルティを重くします。
これにより、正例の検出感度を高めます。
今回はロジスティック回帰(2値分類)の例で考えます。
ロジスティック回帰のモデルは以下で表されます。
P(y_i=1|x_i)=\frac{\exp(\beta_0+\beta^Tx_i)}{1+\exp(\beta_0+\beta^Tx_i)}
また、尤度は以下のように書けます。
L(\beta)=\prod_{i=1}^N\frac{\exp\{y_i(\beta_0+\beta^Tx_i)\}}{1+\exp(\beta_0+\beta^Tx_i)}
負の対数尤度は以下の通りです。
L(\beta)=-\sum_{i=1}^N\{y_i(\beta_0+\beta^Tx_i)-\log(1+\exp(\beta_0+\beta^Tx_i))\}
これは誤差関数と等価であり、$\beta$ を更新してこれを最小化します。(以降、誤差関数と呼びます。)
誤差関数は、正例での値
y_i(\beta_0+\beta^Tx_i)-\log(1+\exp(\beta_0+\beta^Tx_i) \tag{1}
と、負例での値
-\log(1+\exp(\beta_0+\beta^Tx_i) \tag{2}
に分かれます。( $y_i=0$ の場合、(1)の左辺は0になるので省略)
総和の外側でマイナスを掛けているので、総和自体は最大化することが目的です。
学習データが $y_i=1$ (正例)の場合、どうすれば総和が大きくなるでしょうか。
実際に計算してみます。
import numpy as np
z = 1
print(z-np.log(1+np.exp(z)))
> -0.313261687518
z = 5
print(z-np.log(1+np.exp(z)))
> -0.00671534848912
z = 10
print(z-np.log(1+np.exp(z)))
> -4.53988992177e-05
(1)は必ず負の値を取りますが、回帰式
\beta_0+\beta^Tx_i
が大きいほど、その値は大きくなります。(0に近づきます。)
次に、学習データが $y_i=0$ (負例)の場合を考えます。
これは、先頭にマイナスが付いているので、回帰式の最小化が値の最大化となります。
正例と負例の誤差で回帰式を調整することで、誤差関数を最小化します。
表にまとめると以下の通りです。
| 回帰式 | 正例の誤差 | 負例の誤差 |
|---|---|---|
| 大 | 小 | 大 |
| 小 | 大 | 小 |
では、不均衡データの場合はどうなるでしょうか。
データのほとんどが $y_i=0$ (負例)なので、回帰式を最小化するようにばかり学習が進みます。
まれに $y_i=1$ (正例)が出現しますが、この誤差は全体でみると小さいので学習にほとんど影響しません。
表にまとめると以下の通りです。
| 回帰式 | 正例の誤差 | 負例の誤差 |
|---|---|---|
| 小 | 大 | 小 |
| ※学習時、正例の誤差を小さくするモチベーションはほとんどありません。 |
重みの調整というアイデアは、「正例の誤差を小さくするモチベーションを大きくする」というものです。
同時に、「負例の誤差を小さくするモチベーションを小さくする」ことも行います。
具体的には、誤差関数を以下のように変形します。
-\sum_{i=1}^N\{y_i(\beta_0+\beta^Tx_i){\bf w_1}-\log(1+\exp(\beta_0+\beta^Tx_i)){\bf w_0}\}
${\bf w_0,w_1}$ が各クラスの重みです。
${\bf w_1}>1$ の時、正例の誤差が全体に与える影響が大きくなります。
${\bf w_0}<1$ の時、負例の誤差が全体に与える影響が小さくなります。
こうすることで、不均衡データの場合に「全データを負例と分類すれば良い」ということを防ぎます。
クラスの重み
誤差関数にクラス毎に重みを掛けてクラスの誤差を調整すれば良いということが分かりました。
では、どのような重みの値が良いのでしょうか。
これに関しては、絶対的な正解はありませんが、「比率の逆数」が1つの目安となります。
例えば、正例が10件、負例が990件のデータの場合、以下のように調整します。
{\bf w_0}=\frac{1000}{990}=1.01\\
{\bf w_1}=\frac{1000}{10}=100
実験例
sklearnで実験してみました。
sklearnの場合、下記のようにオプション1つで重みの自動調整が可能です。
clf = LogisticRegression(class_weight='balanced')
ドキュメントによると、n_samples / (n_classes * np.bincount(y))の値で重みが調整されるようです。
sklearn.linear_model.LogisticRegression
正例が10件、負例が990件のデータの場合、以下のように調整されます。
{\bf w_0}=\frac{1000}{2\times990}=0.505\\
{\bf w_1}=\frac{1000}{2\times10}=50
まず、以下で人工的な不均衡データを作成します。
import numpy as np
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=1000,
n_classes=2,
weights=[0.99, 0.01],
random_state=1)
念のため確認します。
print len(np.where(y==0)[0])
> 985
print len(np.where(y==1)[0])
> 15
1)重み調整なし
今回、各種ハイパーパラメータはデフォルトとします。
clf = LogisticRegression()
clf.fit(X, y)
y_pred = clf.predict(X)
結果は以下の通りです。
from sklearn.metrics import confusion_matrix
print(clf.score(X, y))
> 0.985
print(confusion_matrix(y, y_pred))
[[985 15]
[ 0 0]]
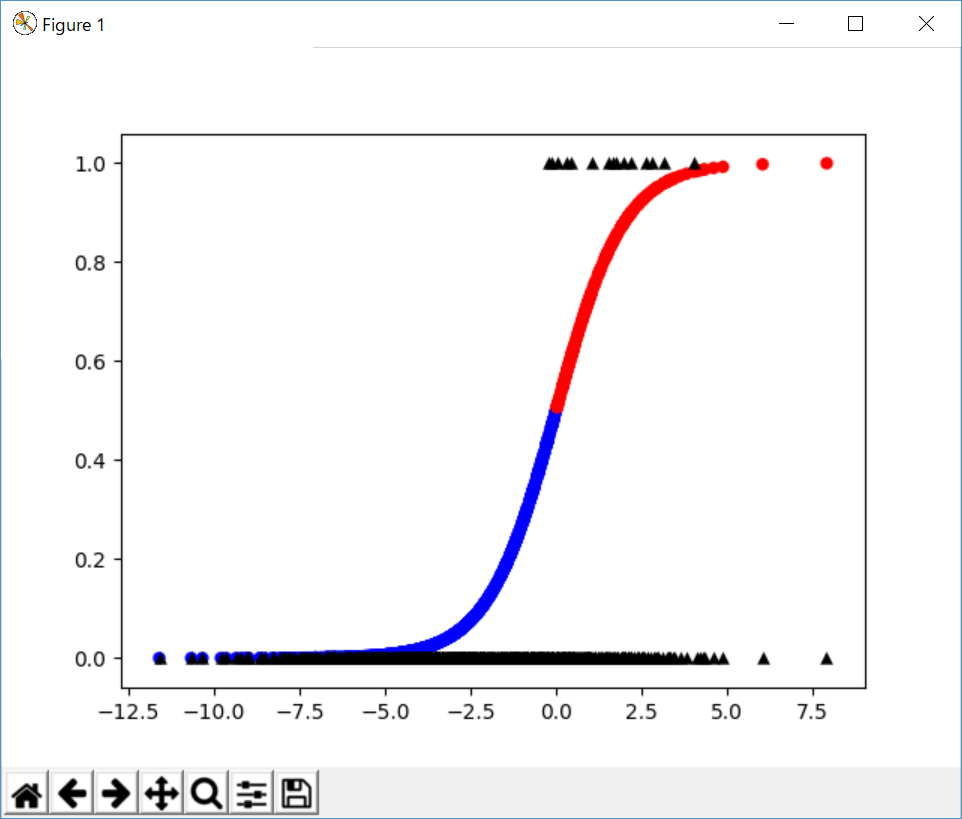
精度は98.5%と非常に高いですが、15件の正例は1つも正解してません。
プロットすると分かりますが、$P(y_i=1|x_i)>0.5$ 以上のデータが1つもありません。
z = np.dot(X, clf.coef_.T) + clf.intercept_
logit = lambda z: 1 / (1 + np.exp(-z))
import matplotlib.pyplot as plt
linewidths = 0.1
plt.scatter(z, logit(z), c=y_pred, cmap='bwr', linewidths=linewidths)
plt.scatter(z, y, c="black", marker='^', linewidths=linewidths)
plt.show()

2)重み調整あり
次に、重み調整結果を確認します。
インスタンス生成時にclass_weight='balanced'を指定するだけです。
clf = LogisticRegression(class_weight='balanced')
clf.fit(X, y)
y_pred = clf.predict(X)
結果は以下の通りです。
from sklearn.metrics import confusion_matrix
print(clf.score(X, y))
> 0.803
print(confusion_matrix(y, y_pred))
[[790 195]
[ 2 13]]
精度は低下していますが、15件の正例のうち、13件正解しています。
重み調整の問題
結果の混同行列を見れば分かりますが、負例のうち、195件を誤って正例と判断しています。
つまり、重み調整なしと比べて、特異度は低下していることになります。
※プロットから分かりますが、そもそも正例・負例が回帰直線で分けることができないので、今回のデータに関してはロジスティック回帰では仕方ない点かもしれません・・
一般に重みの比率を高めるほど、正例の検出感度は上昇します。
※比率を小さくする(「1:1」に近づける)ほど、負例の検出感度は上昇します。
このあたりは問題というより、解きたいタスクに依存する部分かもしれません。
さいごに
今回は不均衡データの重み調整に関して簡単な実験をしました。
重み調整(数が少ない正例の誤差を数が多い負例の誤差と同程度になるよう調整する)が分かれば、データ数の調整(オーバーサンプリング・アンダーサンプリング等)も目的は同じであるということが想像がつきます。
大したものではありませんが、今回のプログラムはここに置きました。