概要
このバズっている認めたくないものだな… Neural Networkの力学系表現というものをに感化され、ODENetについて少しだけ調べておもしれええってなったので備忘録的にまとめます。自分の書いてる内容は薄いです。読める人は原論文読みましょう！
大手のAI研究者は実装もやりつつ、いろんなキャッチアップもしててやはり優秀な方が多いですね！！さすが！！
サクッとなにがすごいのか
参考文献にも出しますが、いろいろなまとめがもうすでに上がっており、非常に勉強になったのでとりあえず細かいところはそちらにリンクを飛ばして、自分の浅はかにもちょっとかじれたところだけを書いていきます。
この辺が素晴らしいのでぜひご覧ください。
- とりあえずの原論文Neural Ordinary Differential Equations
- 論文紹介: Neural Ordinary Differential Equations
- NIPS 2018最優秀賞論文 トロント大学発 ： 中間層を微分可能な連続空間で連結させる、まったく新しいNeural Networkモデル
もうこの画像が全て（ではないけど）ある意味使い古されている原論文[Neural Ordinary Differential Equations](https://arxiv.org/pdf/1806.07366.pdf)の図になります。
もともとニューラルネットは隠れ層をいくつか用意して、ある意味離散的に各層に情報を伝達するような、「とぎれとぎれ」の近似を行なっていたわけです。例えば ResNetでいうと
この更新式ってオイラー近似（時刻$t$ の常微分方程式を解くときのオイラー法）に似てない？となったわけでして、
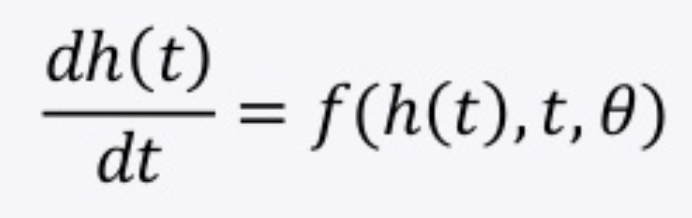この上の常微分方程式をオイラー法で解く際の、$t$を連続的な層情報とすれば、「連続的な」層を持つようなNNが学習できるんじゃ？となったのがODENetになります。
このとき、常微分方程式を解く際の計算量はもちろんどれだけ$t$の幅を細かくとるか、が関わってくるのですが、これは連続的な層をどれだけ粗くとるか、ということと計算量のトレードオフになっています。
論文の提案では、学習の際、バックプロパゲーションをするときに計算グラフをメモリ上に全て保持しなければならなかった従来のニューラルネットの学習ではなく、ODENetを使うことによって計算グラフの保持の必要がなく、常微分方程式のソルバーを使うことでニューラルネット学習しようよ、ということになっています。
論文の１つのメインポイントは、素直にこれを実行した時にやはり保持しないといけない計算グラフを、adjoint-methodを使うことで保持の必要を無くしたというところです。
学習の際に小さくしたいロス関数は、
になりますが、これをパラメータで微分したときの挙動が知りたいわけで、
それをajointと呼ばれる
が従う微分方程式
をソルバーを使って解くことで、メモリに計算グラフを置く必要性を解消しています。
常微分方程式で定式化されるニューラルネット
この解釈めちゃくちゃおもしろいですね！！
原論文の式の導出なども含め、もう少し深入りできるように頑張ります！
おわり。