認めたくないものだな… Neural Networkの力学系表現というものを

この記事は、NTTコミュニケーションズ Advent Calendar 2019の18日目の記事です。
昨日は @yusuke84 さんの記事、WebRTC Platform SkyWayのサポートについて考えていること でした。
メリークリスマス！

はじめに

会社のAdvent Calendarということで、当初はある程度流れに忖度して技術的なTipsを書こう！
とか考えて、Neural Networkについてネタ探ししてたのですが、結局自分が興味のある話、それも実装よりも理論一辺倒な話に落ち着いてしまった、本記事はそんな成れの果てです。
（まあ１人くらい暴走しても良いですよね、きっと）

というわけで、Neural Networkを用いた物理系の表現について、少し前から気になってる話をツラツラと書いていきます。そのうちに、この辺の話を端緒に新規性のある手法を論文化するから、それ相応の評価を会社から頂戴したい、そんなことを妄想しております。（チラッ

※まだまだ期待してますよっ（チラッ（チラッ

おまえ誰やねん！？

普段は技術開発部でデータサイエンス＆AIに資する基礎技術を研究開発している入社２年目社員です。
本垢（ほぼROM専）の方が汚染されているため、こちらの垢@BootCamp_2019からの投稿です。

こちらの垢名から察するに、弊社の社内研修である「BootCamp」の、本年度データサイエンス＆AIコースの講師をしていました。

あとはコトあるごとに「統計検定１級」「数学検定１級」とか、研究業界では差して役に立たない資格を見せびらかしてるアイツです。

会社では多変量時系列解析、スパース推定、要因分析などをメインに研究開発していますが、個人的には非線形力学、縮約理論、情報統計力学とかが好きです。

本記事も結果的に個人の趣味に立脚したものになってしまいました。（てへぺろ

モチベ

最近、いえ少し前から、様々な分野でDeep Learningの応用が議論されるようになってきました。
これは大変喜ばしいコトで、元々数理科学の理論系にいた自分にとってはDeep Learningに本腰を入れる素晴らしいモチベーションになります。
異分野で大切にされている理論やスキームをDeep Learningに取り込むことは、一部で幻滅期に入ったと噂？されるDeep Learningに新しい風を取り込むことと同義であり、多くの視点で次の進化を模索できる素敵なことだと思います。

本記事は、その辺を少し共感して欲しくて書いたものです。

できるだけ平易なモデルと説明でまとめたつもりなので、雰囲気面白いと思ってもらえればありがたいです。
（よく知ってる方は、ぜひ多体位相振動子モデルのHamilton力学を教えてください。今一番気になっています。）

Neural Networkを使った力学系表現

Neural Networkと微分方程式

世界は微分方程式でできている。

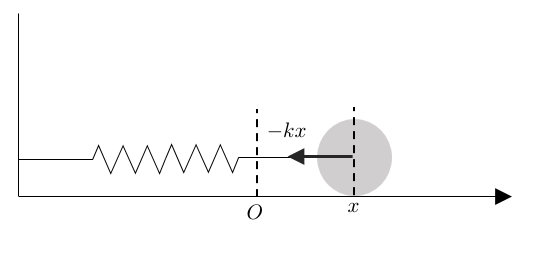
例えば、高校物理で学ぶバネ単振動の運動方程式は以下のように記述されます。
（$m$は質量、$a$は加速度、$k$はバネ定数、$x$は物体の位置で、釣り合いの位置は原点の、シンプルな１次元運動を考えるとします。）
$$
ma = -kx
$$
¹

この先、実はもう少し深く掘り下げて学習すると、物体の速度$v$は位置$x$の１階時間微分であり、また加速度$a$は速度$v$の１階時間微分を意味することを学びます。すなわち、加速度$a$は位置$x$の２階時間微分を意味します。
これを位置が時間の関数$x(t)$であることを明示し丁寧に記述すると、先ほどの運動方程式は以下のように書き直すことができます。
$$
m\frac{d^2x(t)}{dt^2} = -kx(t)
$$

微分方程式（Differential Equation）とは、未知関数とその導関数の関係式として記述される関数方程式のことです。バネ単振動の運動方程式もまさに微分方程式です。

より良い物理現象の理論的解釈には、より良い数学モデルが必要不可欠です。
微分方程式を用いることで、現実世界の現象を（何らかの仮定と近似に基づいて）数学の問題として定式化することができ、その問題の解の意味を解釈することで、元の現象それ自体に理論的な解釈を与えることができます。

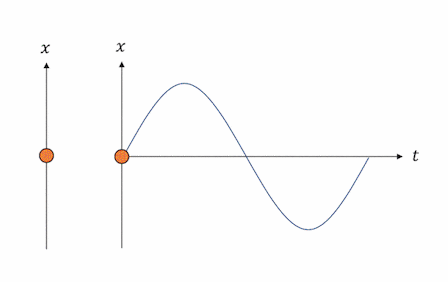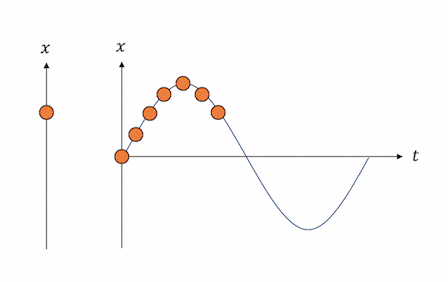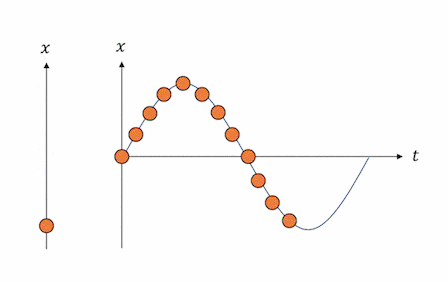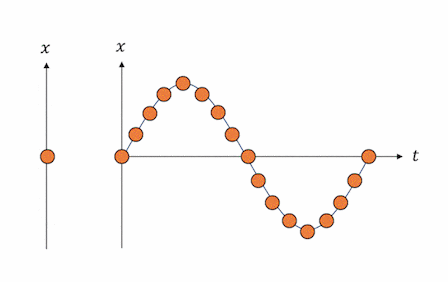
例えば、先ほどのバネ単振動を表現する微分方程式を数学的に解くと、以下のような解を得ます。
（ただし、$A$は振幅、$\alpha$は初期位相で、いずれも初期位置$x(0)$と初期速度$v(0)$から決定されます。）
$$
x(t)=A\sin\left(\sqrt{\frac{k}{m}} t +\alpha\right)
$$
そしてこの解は、下図のように時間$t$と位置$x$の平面でプロットすると、実際の単振動の挙動と見事に一致することが見て取れます。

²

実は微分方程式を用いた数学モデルへの定式化は、何も物理現象のみが対象というわけではなく、生物、化学、政治、経済、社会といった多岐に渡る現象に有用です。
言い換えれば、世の中的な現象は意外すぎるほど微分方程式で表現でき、逆に妥当な微分方程式の発見は現象の理論的解釈と等価な問題と言うことができます。（夢を持って言い切って良いはず！）

とは言え、残念なことに日本の高等教育では、微分方程式の解き方は教えても、微分方程式の作り方はあまり教えられません。解くのは適当なツールを使えば誰でも簡単にできる一方、新しく作り出すのは大変難しく、解くことよりよっぽど重要です。
微分方程式作りに興味のある方は、こちらの書籍³がおすすめです。応用例が非常に多く掲載され、モデル・ビルディングの訓練にも最適な良書です。

微分方程式とResNet

言い忘れましたが本記事で取り扱う微分方程式は、厳密には常微分方程式と呼ばれるグループです。しかし、常微分方程式が何たるか？は長くなるので他所に譲り、メンドくさいので以降も常微分方程式を微分方程式と連呼することとします。

さて、基本の１階微分方程式は一般に以下の形式で与えられます。
$$
\frac{dx(t)}{dt}=f(x(t))
$$
ところで微分は、その定義より以下の極限で求めることができます。
$$
\frac{dx(t)}{dt}=\lim_{\Delta t\to0}\frac{x(t+\Delta t)-x(t)}{\Delta t}
$$
なので微分方程式の挙動を計算機でシミュレーションしたい場合、最も単純には以下のように時間を$\Delta t$間隔で離散化して、離散時刻$t_n=n\Delta t$に基づいて数値計算を行います。
$$
\frac{x(t_{n+1})-x(t_n)}{\Delta t}=f(x(t_n))
$$
これを少し式変形します。
$$
x(t_{n+1})=x(t_n)+f(x(t_n))\Delta t
$$
そして少々天下り的ですが$g(x(t_n))=f(x(t_n))\Delta t$と新しく置き直せば、最終的に以下のように表現することができます。
$$
x(t_{n+1})=x(t_n)+g(x(t_n))
$$
この形式、勘の良いディープラーニング術者はどこかで見たことありませんか？
実はこれ、じっと睨めば画像認識タスクで一世を風靡したResNet⁴と同じ形式の方程式と見ることができます。

逆にニューラルネットワーク側から、順を追ってこの方程式に辿り着いてみます。

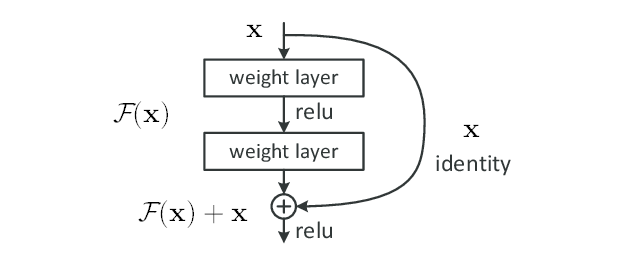
以下はResNet⁴のFigure 2.から引用した図です。

任意のアーキテクチャの各層では、結局のところ何某かの入力$x$に対して、線形変換（Afiine変換など）と非線形変換（活性化関数など）を適当に組み合わせて構成されている、柔軟な非線形変換$\mathcal{F}(x)$を出力とし、次の層へ伝播しています。
図の中央鉛直矢印の伝播経路は、まさにこれを模式的に示しています。（図はReluとありますが、一般にはRelu以外も可です。）

ResNetの肝は右側の「$x$ identity」と記載された伝播経路（迂回路）にあります。
詳細は原論文⁴に譲りますが、この伝播経路（迂回路）は恒等写像で、入力をそのまま出力に合流させます。
それにより、非常に層数の多いネットワークでも効率的に学習を進むことが知られており、その理由は誤差逆伝播が効率的に進むからではないかと考えられています。

ここで、$n$番目ResNetブロックについて入力を$x_n$、出力を$x_{n+1}$とすると、先ほどの図は以下のように書き直すこともできます。

$$
x_{n+1}=x_n+\mathcal{F}^{(n)}(x_n)
$$

これはまさに、先ほど示した離散化された微分方程式そのものと同じ形式の方程式だと言えます。
より明示的に示せば微分方程式内の$x(t_n)$とResNetブロックの$x_n$を対応させれば、わかりやすいと思います。

さらにResNetの一般化として知られるRevNet⁵では、各ブロックは以下のような対称的な構造をしています。

$$
\begin{eqnarray}
x_{n+1}&=&x_n+\mathcal{F}(y_n)\
y_{n+1}&=&y_n+\mathcal{G}(x_n)
\end{eqnarray}
$$
先ほどまでと同様の議論で考えれば、これは次の連立微分方程式を離散化したものとなっていることがわかります。
$$
\begin{eqnarray}
\frac{dx(t)}{dt}&=&f(y(t))\
\frac{dy(t)}{dt}&=&g(x(t))
\end{eqnarray}
$$

ここまでの議論から察するに、ResNet（あるいはRevNet）で全ての微分方程式を記述できるわけではないことに注意が必要です。
この辺の詳細は、最近巷を賑わせているこちらの書籍⁶が詳しいです。この書籍は非常に良書なので、ディープラーニングと物理学の深淵なる関係を探求したい方は、ぜひ手に取ってもらえたら嬉しいです。
特に本記事では議論の簡単化のために、ユニット数などについての考察を端折ったので、こちらの書籍などで詳細は確認してください。

ODENet (Neural Ordinary Differential Equations)

NeurIPS 2018⁷のベストペーパーに選ばれたこちらの論文⁸は、まさに微分方程式で駆動される時間発展方程式とニューラルネットワークを結びつける画期的な手法を提案しています。なお著者実装がGithub⁹で公開されています。

ODENetでは、ResNetやRNNの隠れ層などの層毎の処理を、時間方向に連続極限を取った時間発展方程式と考え、それを（常）微分方程式として陽に解くことでニューラルネットワークを構築するお話です。
連続化することで、深層学習の層という概念がなくなり、メモリや計算量の効率が良く、またBack Propagationに相当する最適化として、（常）微分方程式のソルバーが使えるなど、様々な革新的な手法を提案しています。

こちらはODENet⁸のFigure 1.から引用した図です。左図は通常のResNetで離散的な時間発展を記述している一方で、右図のODENetでは連続的な時間発展を表現できています。そこにはもはや離散的な層の概念がありません。（雰囲気矢印（ベクトル場）多いなあ、と感じていただけると完璧です。）

他にも、 Normalizing Flow¹⁰（NF）を拡張した手法Continuous Normalizing Flow（CNF）で効率的に確率密度が学習できたり、潜在変数の時間発展を連続化することで時系列データを効率的に学習する手法が提案されています。

ODENetについての細かい理論説明はこちらのサイト¹¹¹²¹³がわかりやすいので、ぜひ参照してください。

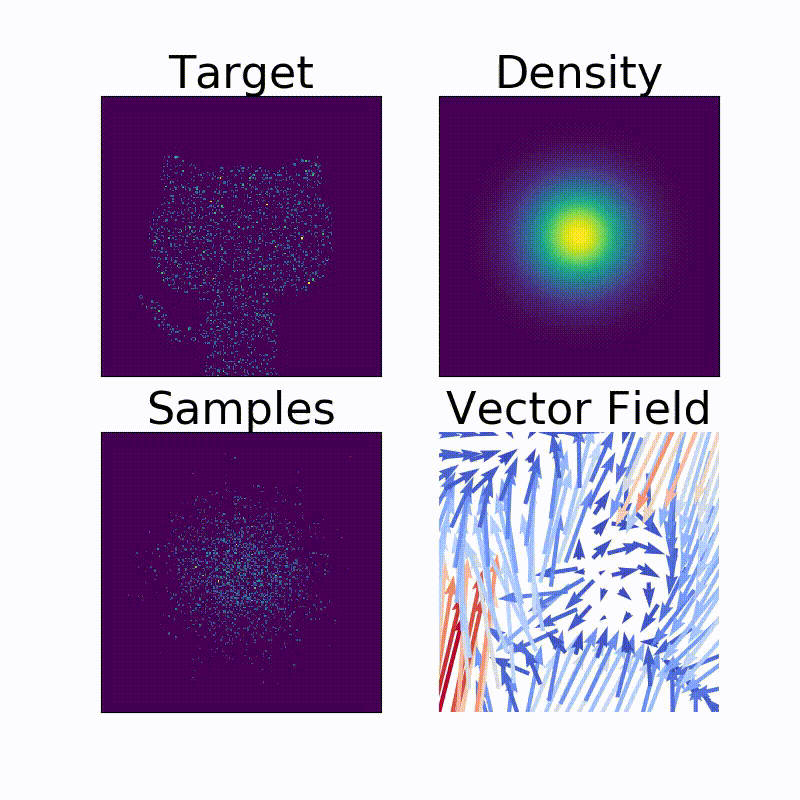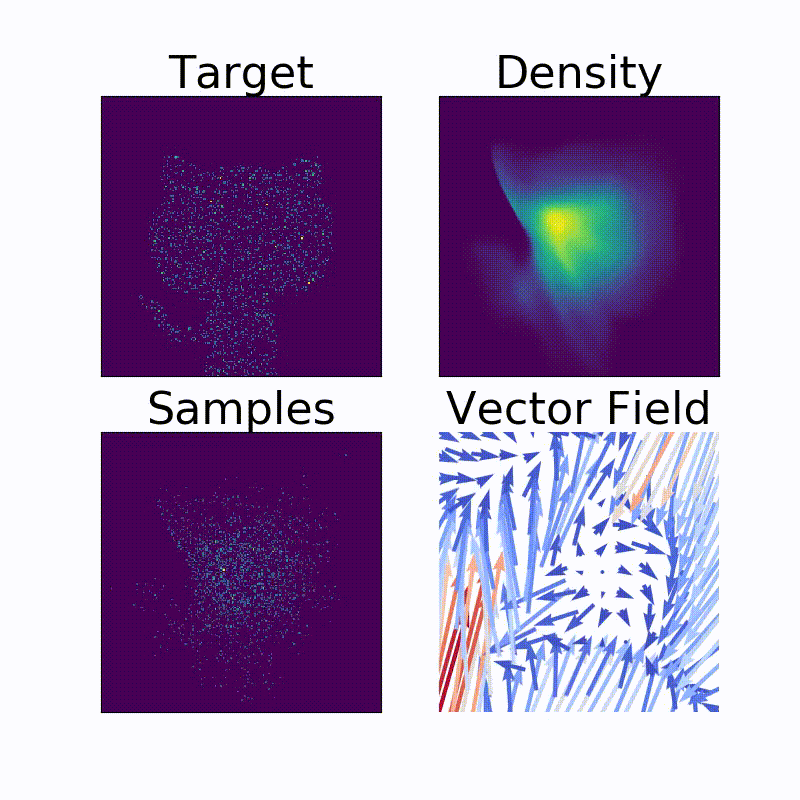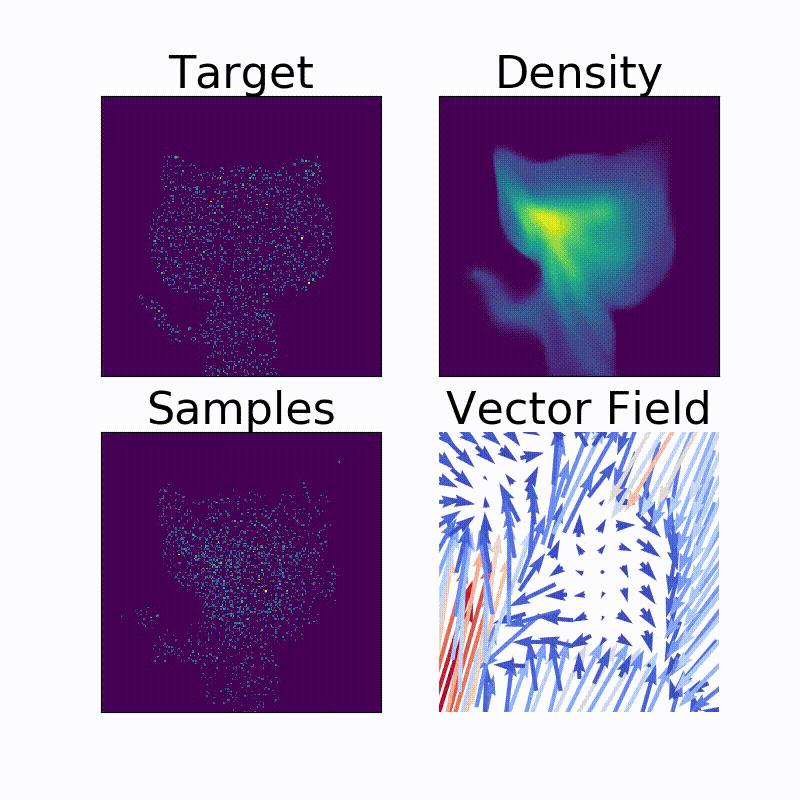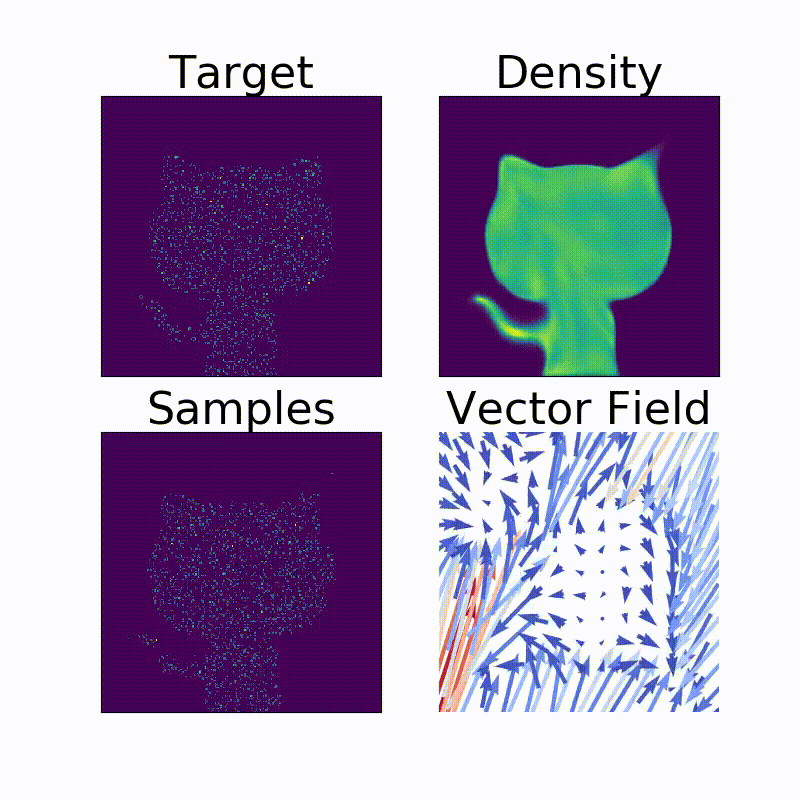
余談ですが、このNormalizing Flow、同じ著者の別のレポジトリ¹⁴でコードが公開されています。実際にヘンテコな確率密度を構成してみると楽しいです。

例えば、我々をいつも暖かく見守ってくれるアイツの確率密度も、こんな風にわりときれいに求めることができます。

Neural NetworkとHamilton力学

Hamilton力学ってなんぞ

Hamilton力学とはHamiltonianという不思議な特性関数を用いて、現象を解析する解析力学の一形式です。
Hamiltonianは物理学におけるエネルギーに相当する物理量であり、物理系の持つ多くの性質をHamiltonianで記述することができます。
（Hamiltonianは必ずしも物理現象のみに限定される概念ではないですが、物理現象を題材にした方が以降の議論がイメージしやすいので、ここではエネルギーだとか言ってます。）

まあ難しい話は棚上げして、高校物理の全エネルギーと等価な物理量だと思うことにします。
すなわち、Hamiltonianと運動エネルギー＆ポテンシャルエネルギーをそれぞれ$\mathcal{H}, \mathcal{K}, \mathcal{U}$と表記すると、以下のように関係性にあります。

$$
\mathcal{H}=\mathcal{K}+\mathcal{U}
$$

もうひとつ重要な概念として、Hamilton力学では一般化座標と一般化運動量が登場します。
とは言え、ここでは簡単に一般化座標は通常の座標、一般化運動量は通常の運動量（質量と速度の積）と考えれば十分です。これらをそれぞれ、$q,p$と表記すると、通常の物理量とは以下の関係で表記できます。

$$
\begin{eqnarray}
q(t)&=&x(t)\
p(t)&=&mv(t)
\end{eqnarray}
$$

とても天下り的ですが、そんな酔狂な表記もあるんだなくらいに思っていただいて、実際にバネ単振動の微分方程式についてのHamiltonianを求めてみます。

これはとても簡単で、運動エネルギーとポテンシャルエネルギーをそれぞれ一般化座標と一般化運動量を用いて、以下のように書き直すだけで十分です。
$$
\begin{eqnarray}
\mathcal{K}&=&\frac{1}{2}mv^2(t)=\frac{1}{2m}p^2(t)\
\mathcal{U}&=&\frac{1}{2}kx^2(t)=\frac{1}{2}kq^2(t)
\end{eqnarray}
$$
すなわち、バネ単振動のHamiltonianは以下のような感じです。
$$
\mathcal{H}=\frac{1}{2m}p^2(t)+\frac{1}{2}kq^2(t)
$$

ではなぜ、Hamiltonianなどという量を導入するのかというと、正準変換や正準方程式という対称性が美しく、然れども便利な関係性があるからです。
もどかしいですが、こちらも詳細は他に譲り、ここでは以下のような関係があると信じることとします。
$$
\begin{eqnarray}
\frac{dq(t)}{dt}&=&\frac{\partial \mathcal{H}}{\partial p}\
\frac{dp(t)}{dt}&=&-\frac{\partial \mathcal{H}}{\partial q}
\end{eqnarray}
$$

そして例として、ひとまずバネ単振動のHamiltonianを適用してみます。
$$
\begin{eqnarray}
\frac{dq(t)}{dt}&=&\frac{\partial \mathcal{H}}{\partial p}=\frac{p(t)}{m}\
\frac{dp(t)}{dt}&=&-\frac{\partial \mathcal{H}}{\partial q}=-kq(t)
\end{eqnarray}
$$

このままでは少しわかりにくいので、一般化座標及び一般化運動量を元の物理量に戻します。
$$
\begin{eqnarray}
\frac{dx(t)}{dt}&=&\frac{mv(t)}{m}=v(t)\
m\frac{dv(t)}{dt}&=&-kx(t)
\end{eqnarray}
$$

最初の関係式は速度が位置の時間微分であることが表現されています。
問題は２つめの関係式ですが、これは実は元のバネ単振動の運動方程式そのものとなっています。
実際に速度が位置の時間微分（最初の関係式）であることを代入してみると、本記事で冒頭に取り上げたバネ単振動の運動方程式と一致することが詳かになります。
$$
m\frac{dv(t)}{dt}=m\frac{d^2x(t)}{dt^2}=-kx(t)
$$

実はHamiltonianには現象を記述する重要な情報が過分に含まれており、（若干の語弊を許せば）Hamiltonianの視点で現象を解析することが、まさにHamilton力学の真髄と言えるでしょう。
ここではバネ単振動の単体運動を取り扱ったのでありがたみが伝わりにくいですが、多体運動や相互結合など複雑な現象になると本領が発揮されてきます。

Hamiltonian（及びLagrangian）については、まずはこの辺¹⁵を読んでみるのが良いかもしれません。

Hamilton Neural Network

ここでは現象を表現するNeural Networkのうち、先ほど紹介したODENetとはまた異なるアプローチを紹介します。
こちらの手法もNeurIPS 2019⁷に採択されており、こちらの原論文¹⁶と著者実装¹⁷で、すぐにお試ししてみることができます。

こちらの手法は直感的には非常にシンプルで分かりやすいです。
Hamilton力学の肝となる正準方程式をそのまま損失関数とすることで、一般化座標と一般化運動量の入力からHamiltonianをうまく表現するようなNeural Networkを学習しています。

ここでポイントとなるのは、良いか悪いかは別として必ずしもHamiltonianそのものを学習しているわけではなく、Hamiltonianに類する何かを学習している点が重要です。
そのため、現象の具体的なHamiltonianが未知の場合でも、その時間発展を上手く表現できるNeural Networkを構成できるものと期待できるのです。

Hamilton Neural Networkの学習の大まかな流れは以下のような感じです。

(1) 時間方向に離散化された一般化座標と一般化運動量を入力データとする。

(2) Neural Networkはパラメタ$ \theta $で特徴付けられているものとする

(3) 順伝播でスカラー値$\mathcal{H}_{\theta}$を出力する（この出力の段階でHamiltonianという要請は特に入れていないことに注意）。

(4) 自動微分を用いた逆伝播で以下の値を算出する。
$$
\frac{\partial \mathcal{H}_\theta}{\partial p},\:\frac{\partial \mathcal{H}_\theta}{\partial q}
$$

(5) 一つ先の時刻の情報を使って一般化座標と一般化運動量の時間微分を求める（これが教師データに相当）。
$$
\frac{dq(t)}{dt},\:\frac{dp(t)}{dt}
$$

(6) 正準方程式に基づいて、以下の損失関数を最小化するように学習する。
$$
L_{HNN}=\left(\frac{\partial \mathcal{H}_\theta}{\partial p}-\frac{dq(t)}{dt}\right)^2+\left(\frac{\partial \mathcal{H}_\theta}{\partial q}+\frac{dp(t)}{dt}\right)^2
$$

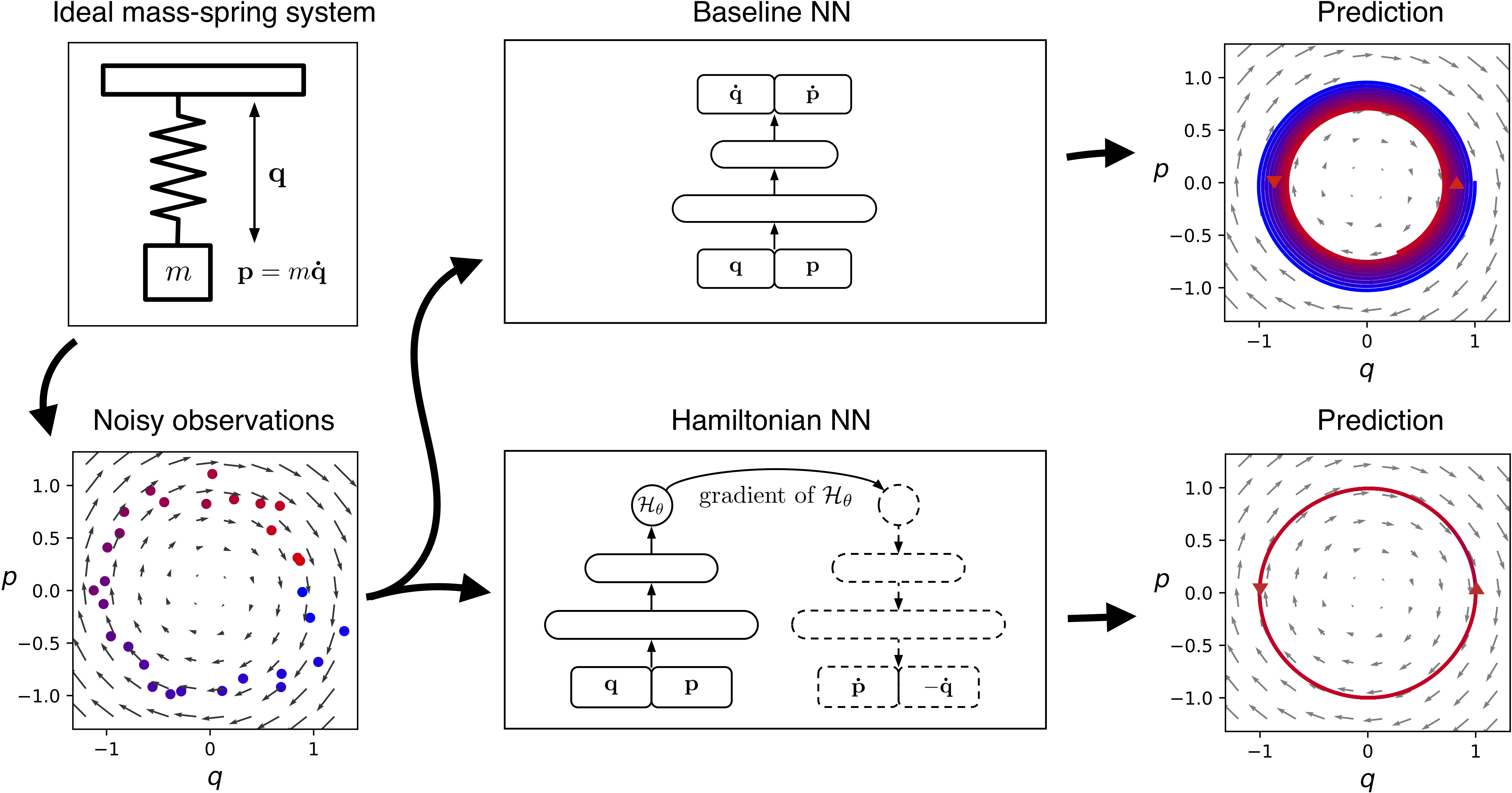
以下はHamiltonian Network¹⁶のFigure 1.から引用した図です。

BaselineとされているシンプルなNeural Networkと比較して、提案手法は元の物理現象の挙動をうまく表現できていることがわかります。

面白い応用としては以下のFigure 4.のように、物理現象の画像データのみを入力としても、現象を上手く再現できているあたりでしょうか。

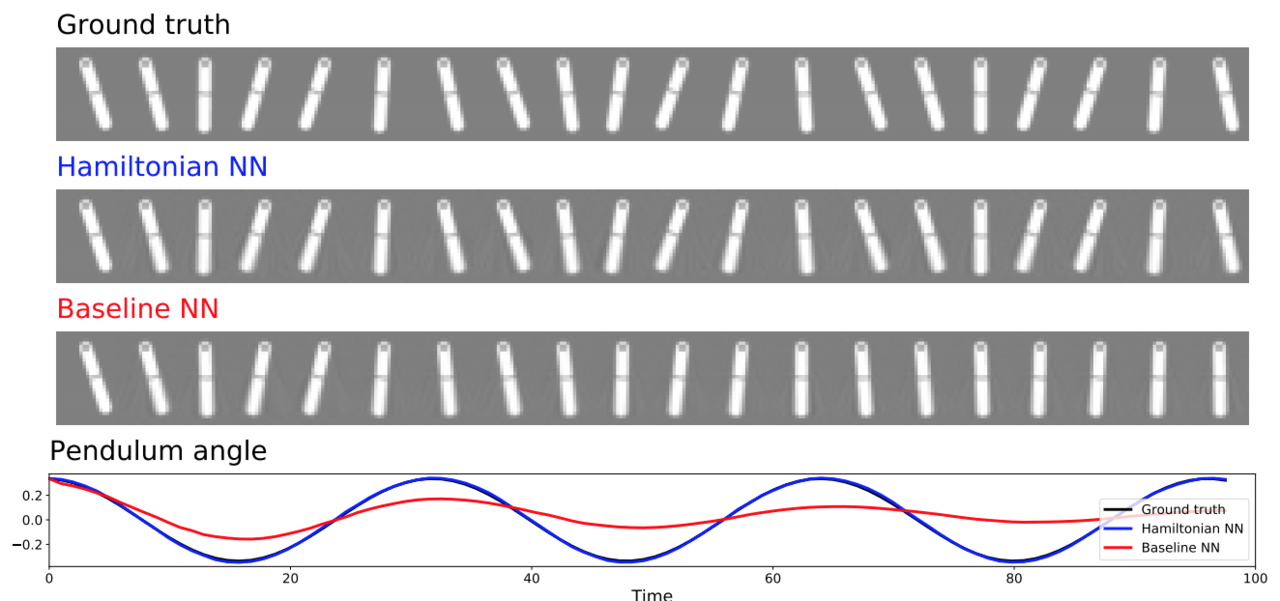
ただ問題としては、単体運動は比較的実測値と等価なものを表現できている一方で、相互作用の働く多体運動に対してはあまり上手く学習できていません。

以下のFigure B.3.を見ると明らかなように、３体運動ではわりと初期の段階から挙動が崩壊しています。（お互いの引力で衝突しそうです。。。）
もっともBaselineと比較すれば、円軌道を保とうとしてる雰囲気を感じられるので比較的よろしいかと思います。

とは言え、とても直感的でシンプルなNeural Networkであるにも関わらず、特に単体運動を具体的に表現できているのは大変興味深いです。まだまだ発展の余地があると思うので、研究開発が捗りますね。

こちらの論文についてはこの辺のサイト¹⁸¹⁹の解説がわかりやすいので適宜参照してください。

まとめ

そんな感じで刺さる人には刺さる内容をまとめた記事でした。
徳の高いまとめを書こうと思ったのですが、今ちょうど会社の開発合宿で南紀白浜に来ており、しかも夕飯食べに行く集合時間まで残り10分を切ってるので、また今度、覚えていたらにしようと思います！お腹空きました。。。

弊チームの神も大浴場から戻られたようなので、一旦ここまでで。

明日は同じチーム＆同じ大学の偉大な先輩@kirikeiさんの大変徳の高い記事です！！！
正座してお待ちしております！！！勉強します！！！

1. わからない物理 運動方程式の解法【単振動】から一部引用。単振動を例に、テイラー展開、指数関数、保存量といった多角的な解法を示し比較している。 ↩

2. 受験メモ 力学の最難関！単振動とは？東大院生が徹底解説！【高校物理】から一部引用。単振動の理論を満遍なく網羅し、図もわかりやすい。 ↩

3. 微分方程式で数学モデルを作ろう, 日本評論社 (1990/4/9). ↩

4. Deep Residual Learning for Image Recognition, Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun, 2015. ↩ ↩² ↩³

5. The Reversible Residual Network: Backpropagation Without Storing Activations, Aidan N. Gomez, Mengye Ren, Raquel Urtasun, and Roger B. Grosse, 2017. ↩

6. ディープラーニングと物理学 原理がわかる、応用ができる, 講談社 (2019/6/22). ↩

7. Neural Information Processing Systems、略してNeurIPS。未だに旧略称NIPSの方がしっくりくる今日この頃。 ↩ ↩²

8. Neural Ordinary Differential Equations, Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, and David Duvenaud, 2018. ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶

9. Github rtqichen/torchdiffeq PyTorch Implementation of Differentiable ODE Solvers、論文⁸の著者実装。 ↩

10. Eric Jang Normalizing Flows Tutorial, Part 1: Distributions and Determinantsがわかりやすい。 ↩

11. SlideShare [DL輪読会]Neural Ordinary Differential Equations、論文⁸の内容が体系的にまとめられている。 ↩

12. Github yoheikikuta/paper-reading [2018] Neural Ordinary Differential Equations、論文⁸の内容についてこちらもわかりやすい。 ↩

13. AINOW 【NIPS 2018最優秀賞論文】トロント大学発 ： 中間層を微分可能な連続空間で連結させる、まったく新しいNeural Networkモデル、論文⁸の内容をとても噛み砕いてイメージさせてくれる。 ↩

14. Github rtqichen/ffjord code for "FFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Models".。こちらはFFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Modelsの著者実装である。 ↩

15. 宇宙に入ったカマキリ 解析力学 ラグランジュ形式とハミルトン形式を適宜参照。特にラグランジュ形式との比較がわかりやすい。
    ちなみに、それ以前の高校物理みたいな話はNewton力学と呼んだりします。 ↩

16. Hamiltonian Neural Networks, Sam Greydanus, Misko Dzamba, and Jason Yosinski, 2019. ↩ ↩² ↩³

17. Github greydanus/hamiltonian-nn Hamiltonian Neural Networks、論文¹⁶の著者実装である。 ↩

18. AI-SCHOLAR エネルギー保存則を満足する物体運動の予測を可能とする Hamiltonian Neural Networks、いつもお世話になっております。 ↩

19. Github yoheikikuta/paper-reading [2019] Hamiltonian Neural Networks、相変わらずわかりやすいです。 ↩