kenmaroです。
秘密計算、準同型暗号などの記事について投稿しています。
秘密計算に関連するまとめの記事に関しては以下をご覧ください。
概要
以前記事にした、格子暗号で新ブレイクスルー!! プログラマブルブートストラップを解説!!
では、プログラマブルブートストラップを実装したCGGI形式の格子暗号を
Zama形式(CGGI亜種)
として紹介しました。
また、記事の最後にはZama ai の開発するライブラリ、
について紹介しました。
今回は、私の理解力(及び低いコーディング力)の範囲内で
このZama形式のモックアップを作ってみた備忘録とし
まとめていきたいと思います。
背景を今一度
プログラマブルブートストラップは、以前の記事ではブレイクスルーであるなどと仰々しく書きましたが、研究の流れからはとても自然に(論文をあと読みすると)想起されたものでした。
実際はCGGI形式と呼ばれる格子暗号をベースに、
BITを対象としていた暗号から実数も暗号上にエンコードできるようなエンコーダを整備し、
実数に対しての関数処理をルックアップテーブルの形でも評価できるようなブートストラップを実装したものでした。(LUT以外の線形的な演算ももちろん可能)
少しわかりにくいですが、ルックアップテーブルを暗号状態で参照することで、
非線形関数をCKKS形式やBFV形式などより簡単に通すことができます。
(しかしながらノイズが上乗せされるのでパラメータの選定は難しい)
オリジナルのCGGI形式に関しては、[0, 1] のビット値をトーラス上にエンコードしていました。これにより、任意の演算をBIT回路まで落とし込み、全てのゲートを暗号状態で準同型的に実行することで、任意の入力に対して任意の関数を準同型評価することを可能にしていました。
ブートストラップは、もともとはノイズが蓄積した格子暗号のサンプルに対し、暗号文を平文に戻すことなくノイズを低減させる、という目的のために使われていました。
それに対してCGGI方式においては、ブートストラップを利用してBITのゲート(たとえばANDや、NORなど)を評価することができ、出力されたビットのノイズの大きさは一定のものに決まっているため、任意回数このようなBITゲートを評価できる、という点でとても画期的でした。
Zama形式で提唱されたプログラマブルブートストラップは、これを実数に(自然に)拡張し、実数の取り扱いを比較的容易にした、というところに新規性があったように思います。また、CKKS方式やBFV方式などではテイラー展開的に近似するしかなかった非線形関数において、LUTを用いて一定の時間で参照評価できる、というところはとても実装側を考えると魅力的でした。
ReLU関数、Max関数などの暗号同士の大小を比較するような関数も、LUTを用いることで評価できるため、AIモデルの推論を準同型暗号を用いて評価するユースケースなどにおいても、とても魅力的だなあと感じていました。
今回やったこと
今回は、後述のCGGI形式ライブラリを軸にし、
実数へのエンコーダ、LUTを評価するプログラマブルブートストラップの処理関数
などをC++で実装してみて、
そのときにZama形式についての実装方法や、実際の取り扱い方などで自分なりに考えたことを書いていきたいと思います。
注意:
私はC++に関しても歴は2年程度、暗号についても専門ではありません、
もしかするといろいろと間違った記述もあるかと思いますがご了承ください。
ベースにしたライブラリ
昨年あたりからキメラ方式
(CGGI方式で使われるトーラス上で、CKKSやBFV方式なども記述し、これらの暗号方式を一般化しようとするもの)
について勉強していた際、virtualsecureplatform というgitレポジトリがあるのを拝見していました。
その当時は一通りソースを読んだりしましたが、CKKS方式などがSEALライブラリで運用されディベロップメントが活発な中、キメラ方式にメリットがあるのかどうか読みきれず、一旦放置していました。
しかしながら、私からしてみれば非常にわかりやすく記述され、かつ使い勝手の良い(比較的触りやすそうな?)CGGI形式のライブラリとして、すばらしいなあと感じていました。
また、彼らが管理されている実装上の講義資料ノート(gitにリンクあり)など、とても理解が深まり感銘を受けました。
今回はプログラマブルブートストラップの文脈において、CGGIベースの暗号についてまた取り組んでみたいと考え、
このTFHEppをベースに、実数へのエンコーダ部分だけでも自分で書いてみようと思い、取り組んでみました。
また、TFHEppは、cuFHE という、
cuda でGPGPUを用いた高速化も開発されており、そこの高速化の恩恵も非常に魅力的だったところも、今回TFHEppを使ってみた理由でした。(私の環境では、GPGPUによるNANDゲートの20倍程度の高速化を確認しました、すごい、、)
結局のところ実装するのはエンコーダ
結局のところ、暗号部分(LWEペアを生成するところ)や、計算部分(FFTなどをいかにエレガントに処理するか)、とてもテクニカルな部分(ブートストラップ鍵の生成や、GSWとLWEの掛け算のところなど)は全てとてもエレガントに実装されているため、
プログラマブルブートストラップを処理するために必要な部分というのは、
実数へのエンコーダエンコーダを加味した準同型演算の関数
のところ(だけ)でした。
もちろん、実装していく中で理解度が足りずに苦戦したところもありましたが、
ベースとなるブートストラップのところまでの実装がしっかりしていたため、
そこには踏み込むことなく上位レイヤとして開発できるのはとてもありがたかったです。
エンコーダの実装
エンコーダの実装に関しても、Zamaの論文
Programmable Bootstrapping Enables Efficient Homomorphic Inference of Deep Neural Networks
を参考にしました。
上の論文と照らし合わせながら実装のポイントなどをまとめます。
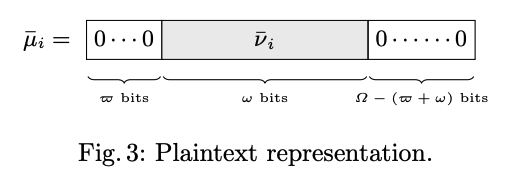
P6に記載の図
のように、Plaintextは、3つのセクションから構成されています。
-
ノイズに使うビット( $ \Omega - (\bar{\omega} + \omega) $ ) ビット -
エンコードする実数(論文ではCleartextと記載)の精度ビット( $\omega$ ) ビット -
パディングビット( $\bar{\omega} $ ) ビット
この$\mu_i $ を論文ではPlaintextと呼び、
実際にエンコードされる実数はCleartextとし、明確に区別しています。
例えばですが、32ビット(uint32_t)を使ってトーラスを記載するのであれば、
(パディングビット、精度ビット、ノイズビット)= (4, 10, 18)
のような設定(一例)となります。
ノイズビットをいくつ使うかはセキュリティパラメータに依存しますし、
パディングビットに関しても、後述の準同型演算、ブートストラップで必要となる(消費される)ため、
いくつパディングビットを持たせるか、というのはパラメータ調整になります。
必要なノイズビットと、パディングビットを使用できるビット数(32、64、128など)から引き算して残ったものがCleartextの精度ビットとなります。
そのため、デフォルトで128ビット長の整数をタイプとして持つRustでの実装(concreteの実装)にも利点があります。
これまでの一連の流れ実装上このようになります。
いくつかの定義
- padding_bit = パディングに何ビット使うか
- $a, b \in \mathbb{R}, a < b $ エンコードするCleartextの範囲
- $ x_c \in [a, b] $ エンコードされるCleartext
- $ x_d \in [0, 1] $ トーラス(0〜1)にエンコードされたCleartext
- $ x_t \in [0, 2^{\Omega - paddingbit}-1 ] \in \mathbb{Z}_q$ トーラス(0〜max(unit32_t) にエンコードされたCleatext)
- $ \mu \in \mathbb{Z}_q$ x_tにノイズなどを加味したPlaintext
エンコード手順
実装上の流れは概ね以下のようになります。
- Cleartextの取る範囲を設定 [a, b] (a,b はdouble)
- x_c $ \in [a, b] $ (エンコード対象のCleartext ) をトーラス上の点 x_d $ \in [0, 1] $ にマッピング
- x_t $ \in [0, 1] $ に $2^{\Omega - paddingbit} $ を掛け算 して x_t $\in \mathbb{Z}_q$ にマッピング
- x_t, 設定したビットにしたがってPlaintextを生成 ( $x_t$ )
- Upper関数によってトーラス上(uint32_t、もしくはunint64_t 上の整数)にマッピング ( $\mu$ )
すなわち、
$ x_c \in [a, b] \longrightarrow p_t \in \mathbb{Z}_q$
にマッピングします。
デコーダの実装
エンコーダの逆となる操作を実装するだけです。
すなわち、
$ \mu \rightarrow x_c $
にマッピングします。
このとき、準同型で評価した関数や、ノイズの大きさに寄与したround する時の誤差が発生しますが、
それは CKKS形式と同じように計算で発生した(浮動小数点を使った計算と同じような)誤差として解釈します。
具体例
例えば、$Encoder(a=-10, b=10, padding_bit=1)$
で設定した場合、$\Omega = 32$ として、
plaintext の取る値は $[0, 2^{31} - 1 ] $ となります。
もしエンコードしたいCleartext が $x_c = 2$ だった場合、
$ x_d = 2/20 = 0.1 $
$ x_t = round(2^{31} * 0.1) = 214748365 $
となります。これにノイズ( $\in [0, 2^{noisebit}-1] $ ) を加えたものがPlaintext $\mu $ となります。
$p_t$ のとりうる範囲
$x_t$ にノイズを付与した値を$p_t$とし、
これがPlaintextとして実際に暗号化されます。
この時の$p_t$の値が、暗号文のPhaseと呼ばれるわけですが、
このPhaseは前述の通りトーラス上で定義されています。
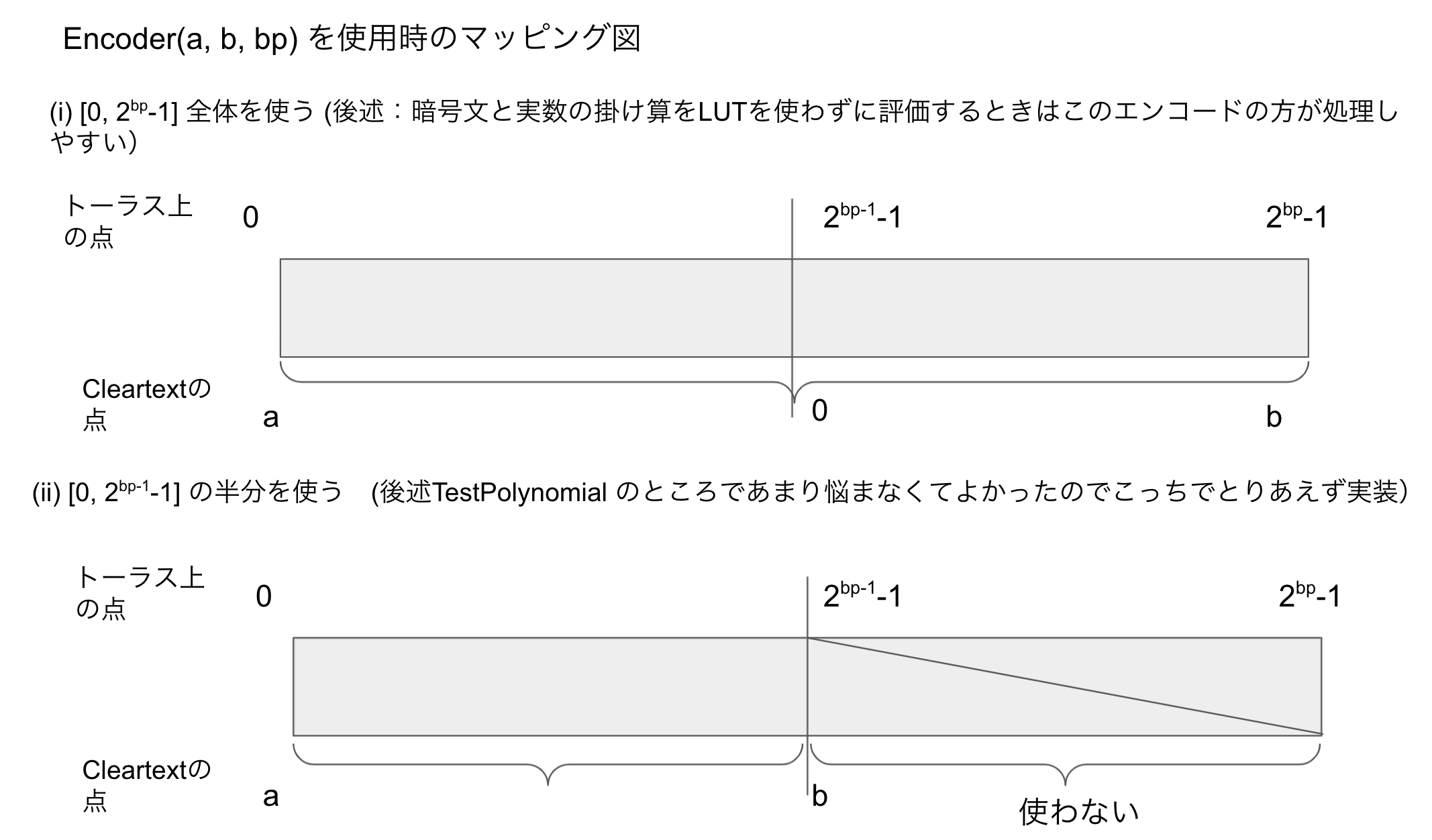
エンコーダのbpを、$x_t$ がとりうる$\in [0, 2^{bp} -1]$と対応させた図が上図となります。
Zamaの実装では(i)のマッピングがされています。
今回は後々TestPolynomialの作り方で詰まったので、(ii)のエンコーダを使っています。
このエンコーダの書き方に関しては簡単に変更ができるので、まあとりあえず(ii)を使ってみました。
暗号化、復号などの処理
$ \mu $ が生成されたあとは、もうトーラス上の点にマッピングされていることから、
すでにCGGI形式で実装されているLWEペア生成などをいつも通りに実行することで
暗号化、復号ができます。
なぜパディングビットを使うのか
暗号文同士の足し算や引き算
パディングビットを使う(padding_bit > 0) ということは、
x_t のとりうる範囲を使っているuint32_tなどの整数全体ではなく、 $ [0, 2^{paddingbit} - 1] $ に限定しています。
これがなぜ必要かというと、暗号文に対して加算乗算などをLUTを使わずに行うとき、
padding_bit を消費する必要があるからです。
暗号文同士の足し算や引き算を行う時、パディングビットを1消費し、
encoderのa, b を拡張します。
たとえば $x_c \in [-10, 10]$, $x_c2 \in [-10, 10]$ の足し算をするのであれば、
結果は $x_cadd \in [-20, 20]$ に落ちてくる可能性があるので、
エンコーダのa, b を(-20, 20)に再設定します。
また、$x_t1 \in [0, 2^{\Omega-paddingbit}-1]$, $x_t2 \in [0, 2^{\Omega-paddingbit}-1]$
どうしの足し算が行われるので、結果の $x_tadd$ はもちろん $[0, 2^{\Omega-paddingbit}]$ をとり得ます。
したがって、足し算、引き算をする時のためにパディングビットは設計されている必要があります。
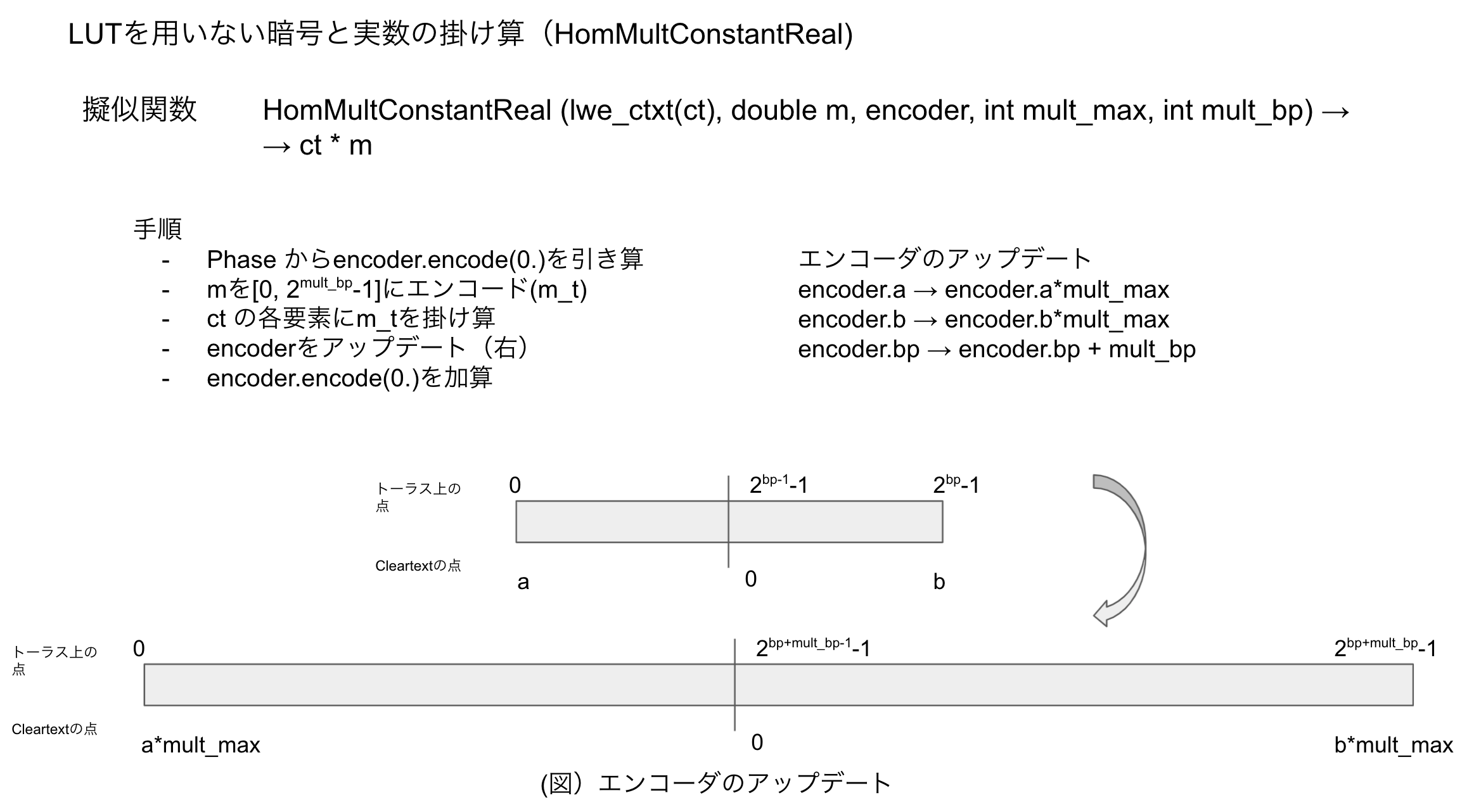
暗号文に実数(平文)を乗算する時
実数を掛け算したい時、たとえば1.2を掛けたい時などは、パディングビットを一定数消費する必要があります。
やっていることはとても単純で、
新しくPhaseが使用するbitをpadding_bitを消費することで確保し、エンコーダを書き換えます。
- 掛け算する実数のmax値 (mult_max)
- 掛け算するときに消費するビット数 (mult_bp)
- 掛け算する実数 x
を用意します
初めに、対象となるTLWEのPhaseを $encoder.encode(0.0) $ だけずらします(引き算)。
次に、xを以下のようにマッピングします。
$x \rightarrow x_t$
where $ x/max \in [0, 1] \rightarrow x_t = x/max* 2^{multbp} \in [0, 2^{multbp} - 1] $
その後、LWE暗号文の全ての要素に $x_t$ を掛け算します。
最後に、エンコーダをアップデートし、$encoder.encode(0.0)$ 分だけTLWEのPhaseをずらし直します(足し算)。
プログラマブルブートストラップの手順
TestPolynomialの作り方
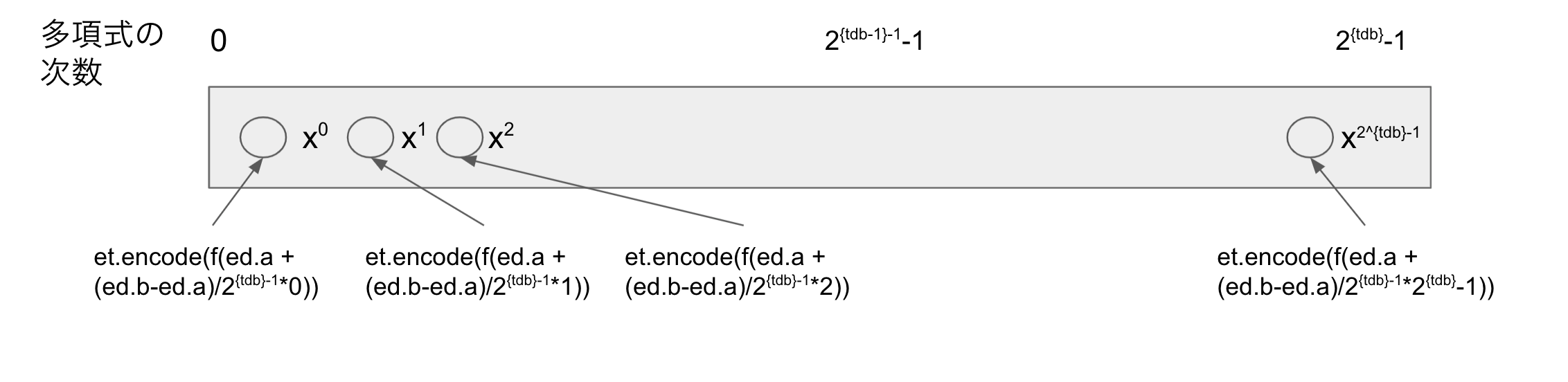
TestPolynomialは、暗号状態で参照するLook Up Table (LUT) です。
生成には、LUTの対象となるLWE暗号文に付随するエンコーダ(encoder_domain) と、
プログラマブルブートストラップ後のLWE暗号文に付随するエンコーダ(encoder_target)を対応させる必要があります。
つまり、encoder_domainが許容する $x_d$ の範囲 $ \in [a,b]$ が、encoder_targetでの $x_t \in [0, 2^{target.bp}-1]$ にどう対応するかをマッピングする必要があります。
実際に多項式を生成するときは、function f を施した数が、
encoder_targetでの $x_t \in [0, 2^{target.bp}-1]$
にどうマッピングされるかを、encoder_domainの範囲$ \in [a,b]$ にしたがって係数に挿入します。
気をつけること
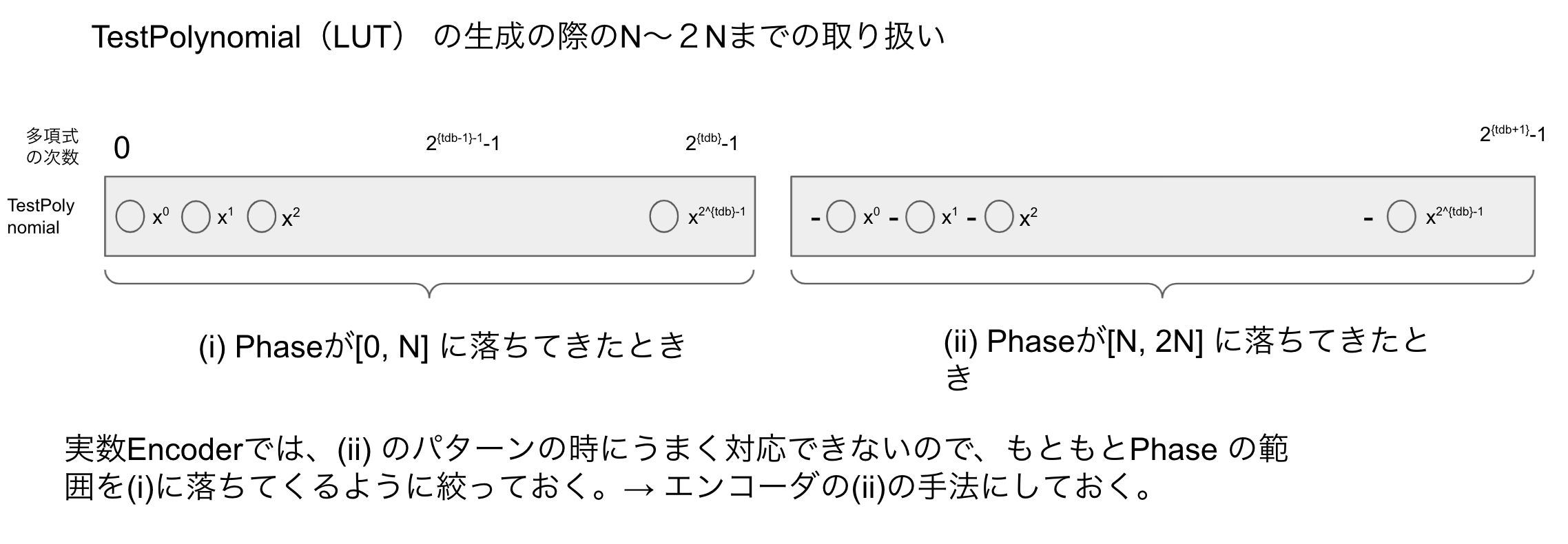
Zamaの論文では、TestPolynomialのサイズが N と表記されています。
ここでは $N=2^{tbp}$ としています。
BlindRotateをした時に、Phaseが[0, N] で落ちてくればマイナスはつかないのですが、
[N, 2*N] で落ちてきた時には、係数にマイナスがかかっていることになります。
(これは $ X^{N} + 1 $ で割った時の剰余多項式環を格子として使用しているため。)
したがって、マイナスがついてしまうと実数エンコードの時には対応できない(不本意な値がPBSの結果として得られてしまう)ため、もともとPhaseが[0, N]にしか落ちてこないようにエンコーダが使用する範囲を絞っておく必要がある。
今回では、Encoderの使用を(ii)の仕様にしました。
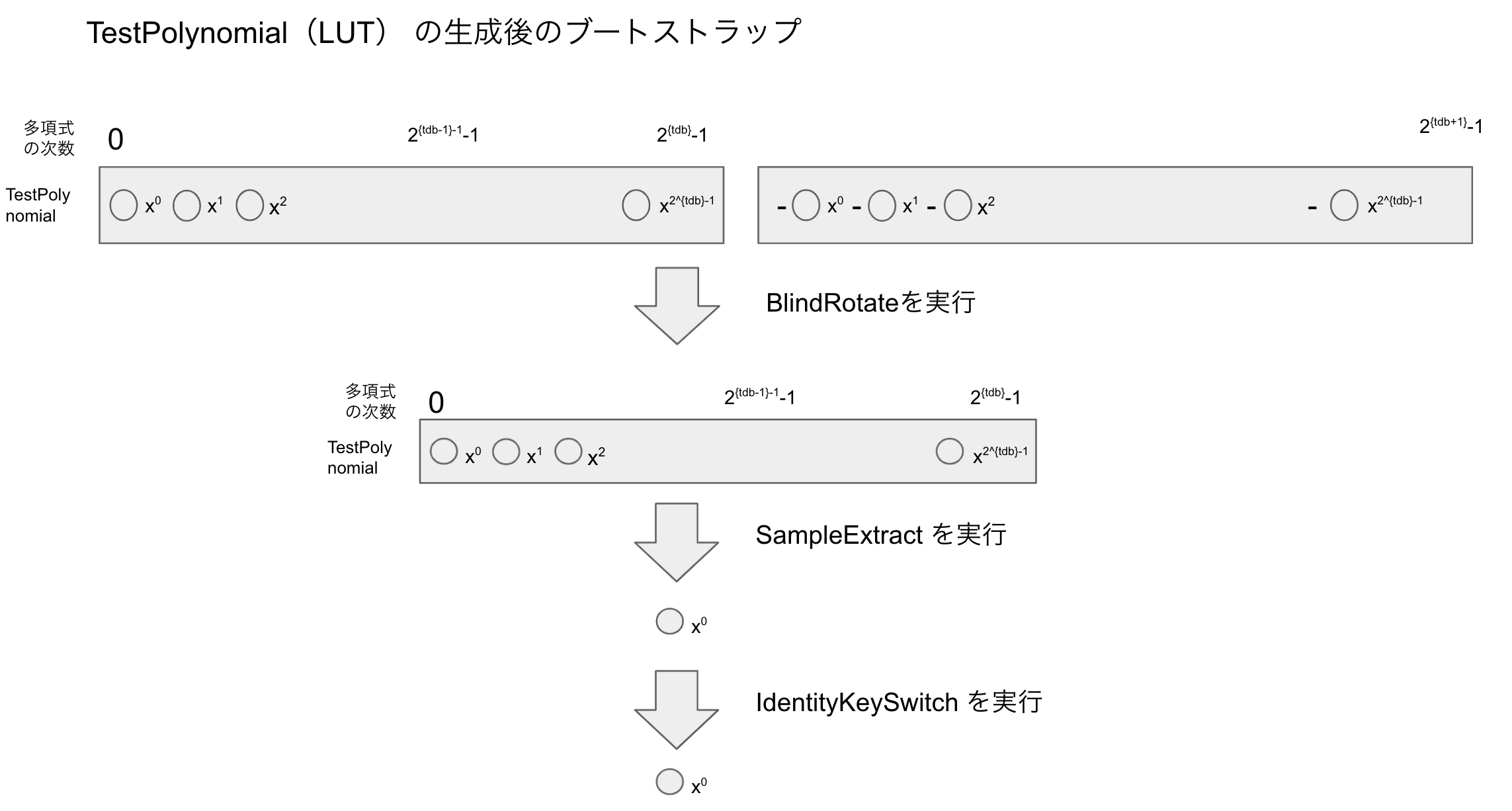
ブートストラップの実行
これはTFHEppに実装されているものをそのまま実行する形でした。
BlindRotate後、SampleExtractを実行、IdentitiyKeySwitch を実行することで、
鍵をオリジナルなものに戻し、ブートストラップの全体が完了となります。
(ブートストラップにはもともとの鍵を暗号化する2つ目の鍵を使うため、SampleExtractしたあとの暗号文は暗号鍵2で暗号化されたものになっています。したがって、IdentityKeySwitchを実行することで、暗号鍵1で復号できるように暗号文を改変します。)
いくつかの注意点
もしかすると改善できるのに気づいていない可能性がありますが、
とりあえず注意する点について書き出します。
ブートストラップ後はパディングビットが0になる
ブートストラップを実行すると、phaseは
$phase \in [0, 2^{Omega}-1] $
すなわちパディングビットは0になります。
つまり、ブートストラップ後にパディングを消費するような演算は不可能になってしまいます。
したがって、ブートストラップ後に演算を行いたい場合は、全てLUT経由の演算になります。
もしくは、padding_bitを消費しないような演算であれば可能。
トーラス上の点 $x_t$ の整数部分に注意
トーラス上の点(x_t) をx_dに変換するとき、
$x_d \in [0, 1]$ がきちんと守られているかどうかチェックする必要があります。
もし $x_d \in R$ になっている際は、HomMultRealなどの演算をする時に値が保存しないので、バグの原因となります。
実装したコード
ここにフォークレポジトリを上げています。
あくまでテスト実装ですので、とても汚いコードになってしまっていますが、
少しきれいにしようかと思っています。
tutorial/mytest4.cpp
などを見ていただければ、何をやろうとしているのかは理解できるかと思います。
//mytest4.cpp の抜粋
int main(){
printf("hello, world\n\n");
// ブートストラップ用のエンコーダ設定(前述のように、BSの後はpadding_bitが0になるため、bp=32)を使用。(トーラスは128.hppの設定によってunit32_tで記述されている)
double encoder_a = -100.;
double encoder_b = 100.;
int bs_bp = 32;
TFHEpp::Encoder encoder_bs(encoder_a, encoder_b, bs_bp);
// generate a random key
std::unique_ptr<TFHEpp::SecretKey> sk =
std::make_unique<TFHEpp::SecretKey>();
// Identity Key Switch において、encoder情報が必要なため、それを加味してKey Switch Keyを生成する。
std::unique_ptr<TFHEpp::GateKey> gk =
std::make_unique<TFHEpp::GateKey>(*sk, encoder_bs);
double x = 1.6;
double x2 = 0.6;
double d, mult;
// c1 に付随するエンコーダ encoder
Encoder encoder(-100,100,32);
// c2 に付随するエンコーダ encoder2
Encoder encoder2(-100,100,32);
// エンコードしてPlaintextを暗号化
TLWE<lvl0param> c1, c2, c3;
c1 = TFHEpp::tlweSymEncodeEncrypt<lvl0param>(x, lvl0param::alpha, sk->key.lvl0, encoder);
c2 = TFHEpp::tlweSymEncodeEncrypt<lvl0param>(x2, lvl0param::alpha, sk->key.lvl0, encoder);
// 復号してデコードすることで実数を得る。
d = TFHEpp::tlweSymDecryptDecode<lvl0param>(c1, sk->key.lvl0, encoder);
printf("original %f = %f\n",x, d);
encoder.print();
// Decode(Decrypt(Encrypt(Encode(x)))) と x の比較
printf("\n===============================\n");
for(int i=i; i<20; i++){
double x = encoder_a + encoder.d/2./20.*double(i);
TLWE<lvl0param> c1 = TFHEpp::tlweSymEncodeEncrypt<lvl0param>(x, lvl0param::alpha, sk->key.lvl0, encoder);
double d = TFHEpp::tlweSymDecryptDecode<lvl0param>(c1, sk->key.lvl0, encoder);
printf("x %f = %f\n",x, d);
}
// 10回暗号文に対してブートストラップをかけ、driftエラーの大きさを見てみる。
printf("\n===============================\n");
for(int i=0; i<10; i++){
if(i == 0){
TFHEpp::ProgrammableBootstrapping(c1, c1, *gk.get(), encoder, encoder_bs, my_identity_function);
d = TFHEpp::tlweSymDecryptDecode<lvl0param>(c1, sk->key.lvl0, encoder_bs);
printf("bs %f = %f\n",x, d);
TFHEpp::ProgrammableBootstrapping(c2, c2, *gk.get(), encoder, encoder_bs, my_identity_function);
d = TFHEpp::tlweSymDecryptDecode<lvl0param>(c2, sk->key.lvl0, encoder_bs);
printf("bs %f = %f\n",x2, d);
}else{
TFHEpp::ProgrammableBootstrapping(c1, c1, *gk.get(), encoder_bs, encoder_bs, my_identity_function);
d = TFHEpp::tlweSymDecryptDecode<lvl0param>(c1, sk->key.lvl0, encoder_bs);
printf("bs %f = %f\n",x, d);
encoder_bs.print();
}
}
// プログラマブルブートストラップを使用して、平文の定数(0.9)と掛け算を行ってみる
//printf("\n===============================\n");
//for(int i=0; i<5; i++){
// mult = 0.9;
// TFHEpp::ProgrammableBootstrapping(c1, c1, *gk.get(), encoder_bs, encoder_bs, my_multiply_function, mult);
// d = TFHEpp::tlweSymDecryptDecode<lvl0param>(c1, sk->key.lvl0, encoder_bs);
// printf("mult %f = %f\n",x*pow(mult,i+1), d);
//}
// プログラマブルブートストラップを用いて、Max(c1, c2)を計算してみる
TLWE<lvl0param> test1;
//TFHEpp::HomADDFixedEncoder(test1, c1, c2, encoder_bs, encoder_bs);
//TFHEpp::HomSUBFixedEncoder(test1, c1, c2, encoder_bs, encoder_bs);
TFHEpp::HomMAX(test1, c1, c2, encoder_bs, encoder_bs, encoder_bs, *gk.get());
d = TFHEpp::tlweSymDecryptDecode<lvl0param>(test1, sk->key.lvl0, encoder_bs);
printf("max of (%f, %f) = %f\n",x,x2, d);
//printf("sum of (%f, %f) = %f\n",x,x2, d);
return 0;
}
現状
Zama の論文では、BSを行った時の丸め誤差のことをdriftエラーと呼んでいますが、
128.hppに設定されているパラメータだと、driftが大きくなりすぎています。
パラメータによってこれをまだ改善できるのかまだよくわかっていません。
これがもう少し小さくできれば実用できそうな気もします。
まとめ
今回はVirtualSecurePlatform の開発する
TFHEpp(トーラスベースの暗号ライブラリ)を低レイヤとして、
Zama方式のエンコーダを
実装する上でどのようなことが必要なのかを理解するために実装してみた、
というような内容でまとめてみました。
セキュリティビット128だとdriftエラーが非常に大きい(現状)ため、
パラメータのことや、内部の実装のところなどもう少し精査してみたいと思いつつ、
ここまでで結構疲れたので一旦記事にさせていただきました。
プログラマブルブートストラップについて実装、もしくは使ってもっと上位レイヤの開発を考えている方、
concreteをひとまず触ってみるのもありですし、CGGI形式のライブラリを軸に、自分でエンコーダ部分を書いてみるのもありだと思います。(書いてみると理解が深まります。。)
今回はこの辺で。
kenmaro