@kenmaroです。
普段は主に秘密計算、準同型暗号などの記事について投稿しています。
秘密計算に関連するまとめの記事に関しては以下をご覧ください。
概要
SVRを準同型暗号を使って推論しようとしたとき、
あれ、SVRってどのようなアルゴリズムだったっけ、、
となってしまい、調べてみたのでわかったことを簡単にまとめようと思います。
このように、Scikitlearnでは1行で書けるようなプログラムであっても、
いざ暗号を適用しようとすると、その内部アルゴリズムを学び直す機会が必要となり、
あー、案外何もわかってなかったなぁ、となったり、
以前勉強したはずだったけどほとんど忘れてた、、
となったりする毎日です。
また、以下の記事を(2年前か、、)に書いた時のことを思い出しながらこの記事も書いてみようと思います。
ResNet なんて全く理解していないだけの人生だった(序)
上の記事は「ResNetの少し普通とは違う角度からの捉え方」
について非常に面白いな、と思ってまとめてみたものでした。
SVRについても似たように、ちょっと違う角度から捉えられるかもしれない、
と思ったところ、とても細部まで解説してある文献を見つけたので、そこで学んだことをまとめていければと思います。
証明や式等はその文献をみていただければと思います。
筑波大学の高野先生が書かれた文献です。
では、始めます。(最後に秘密計算での応用もちょっとだけ書きます。)
SVM と SVR
SVMは言わずと知れたサポートベクターマシンであり、
2値分類をする際によく使われる手法です。
SVRはサポートベクター回帰であり、コアとなるカーネル関数を用いたモデルであるというところは同じです。
回帰なので連続値を(たとえば身長とか、気温とか、)を推論するようなモデルの、サポートベクターマシンの拡張版と言っていいでしょう。
カーネルについて
SVMについての解説記事等はたくさん存在し、とてもわかりやすいものが転がっているため、
そちらを参考にされることがいいと思いますが、
本質的に大事なのは「カーネル関数」(証明まで読みたい人は「表現定理」も)となります。
SVMでは2値の分類をする際に、もともとの説明変数を特徴量空間へと「非線形に」変換することが必要であり、どのような変換をすれば2値分類をできるような超平面を引くことができるだろうか?
というところに焦点を当てています。
超平面を引くことでその平面で分断される空間の片方に存在するデータ点は推論値0、
もう片方に存在するデータ点は推論値1、というふうに2値分類を行うことができるわけです。
目的関数の最大化(最小化)
SVMについても、SVRについても、機械学習モデルには、最少化すべき目的関数(ロス関数)
が存在し、SVMでは、超平面と、分けられたデータ点との(平面と一番近いデータ点の)距離を最大化するという条件、
SVRでは回帰結果で出てくる値の差異をなるべく小さくする、
という条件を制約条件とともに書き出したものが目的関数になっています。
特徴量空間とカーネル関数
上記の目的関数を定義するのは、説明変数を非線形変換した後の「特徴量空間」においてでした。
非線形変換をする、ということは、説明変数の2乗の項や、3乗の項、
各変数を掛け合わせたものなど、いろいろな組み合わせを生成し、それらの線形和を用いて、
特徴量空間を定義し、その空間にマッピングをするということですが、
どの組み合わせがいいのかを無限次元までの組み合わせで考えることになってしまいます。
これは不可能ではないですが、計算量が膨大になってしまう、という問題がありました。
ここで、「特徴量空間上での二点の内積」を表現するような関数を「カーネル関数」が登場します。
初めはカーネル関数を定義するとなにがおいしいの?
と思っていましたが、このカーネル関数を定義することで、先ほどの目的関数の最少化、
という問題が驚くほどシンプルな式でかけることになります。
表現定理によるすり替え
そもそも、目的関数は特徴量空間で記載されるため、目的変数の最小化、というのはまずどのような特徴量空間にマッピングすればいいか、を初めに考えないと始まらないものであったのですが、
カーネル関数を登場させることで、実際にどのような特徴量空間にマッピングすればいいかを考えることなく、目的関数の最小化を考えることができることになります。
この問題の「すりかえ」ができることを証明するのが「表現定理」であり、
興味のある方はぜひ証明も追ってみてください。
SVRの別の角度からの見方
カーネル関数とは結局、、?
結局のところ、「表現定理」を用いた後に出てくる式は、
目的の推論を実行する式、つまりもともとの説明変数を入力とし、正解ラベル(もしくは正解値)を当てるような最適な式
というのは、n個の学習データに対して、入力データとのカーネル関数をそれぞれ計算し、重ね合わせた値となる、ということになります。
この記事に言及されていますが、結局のところカーネル関数は、入力データに対して、学習サンプル一つ一つと類似度を計算し、その類似度の重ね合わせを持って推論値を叩き出すような式になっています。
kNNと似てるのでは??
学習サンプルともし入力データの類似度が高ければ、推論値もその学習サンプルのラベル値と近くなるはず、
というのは感覚的にもわかりますし、それを全サンプルに対して調べるわけですから、
ある種のkNN(k近傍法)的な考え方と近いのでは??
と思うわけです。
特徴量空間ってNNでも作れるのでは?
また、もう一つ視点から考えてみると、結局のところ、カーネル関数を考えることにより
非線形空間にマッピングしているんでしょ?ということは普通にニューラルネットで特徴量空間へと全結合層を使ってマッピングし、その空間から線型空間を担当する1層の全結合を介するNNと何が違うんだろう?
と思いますよね?
kNN, SVR, NN のつながりを見る
上で出てきた、
- なんかカーネル関数は結局のところ学習サンプルと入力データの類似度をとっていることが本質だよね、
とか、 - 非線形空間に一度マッピングを行い、その空間の中で線形変換を行うという本質のあるSVRは、結局のところNNと同じでは?
という疑問に対して、高野先生の文献はそこにも言及しています。
端的にまとめると、
SVRを考える際の、カーネル関数を特殊なもの(1/K と言う定数、Kはクラスタ数)にし、
カーネル関数の重ね合わせに出てくる係数(文献ではアルファ)については学習サンプルのラベル値を採用すると、その特定のカーネルで考えられたSVRは、
kNNそのものになります。
また、隠れ層一層の簡単なNNを考えた際に、
隠れ層の次元をサンプル数と同じにし、活性化関数をシグモイドにすると、そのNNは
カーネル関数をシグモイドカーネルで定義した時のSVRと同じものになります。
言われてみればいや、そんなの当たり前だよ、と思う方も多いかもしれませんが、
私としてはなにか複数のアルゴリズムが線でつながったような気がしてとてもスッキリしました、笑
せっかくなので少しだけ準同型暗号での実装について
このようにSVRとはなんぞや、と言う理解が深まったところで終わってもいいのですが、
せっかくなのでこれを準同型暗号(格子暗号)を用いてどうやって実装するか、というフロー図だけ簡単に解説して終わろうと思います。
Scikitlearnを用いると1行で完了してしまう推論処理ですが、
暗号を使うとなると、内部で実際にどのような処理をしているかを一度分解処理する必要が出てきます。
Sklearn ではpython にてこのクラスをインポートすることでSVRを実装することができます。
from sklearn.svm import SVR
上が公式のSVRのドキュメントですが、
推論時にはどのような処理が走っているのでしょうか。
regr = SVR(C=gridsearch.best_params_["C"], epsilon=gridsearch.best_params_["epsilon"])
このような感じでSVRのインスタンスを立ち上げ、 fit すると学習自体は簡単に実行することができます。
このあと、
regr.support_vectors_.shape
を実行すると、
(サポートベクターの数、入力データ説明変数の次元)
が得られます。
これは、推論時に使うのですが、
カーネル関数を「学習サンプル全て」と計算するのではなく、「サポートベクターのみと」計算することになります。
したがって、predict 関数を使わないようにしてSVRの推論を行う際は、
# 訓練データを基準に標準化(平均、標準偏差で標準化)
scaler = StandardScaler()
X_norm = scaler.fit_transform(X)
# テストデータも標準化
Xtest_norm = scaler.transform(Xtest)
# ここから推論パート(暗号化した状態で以下を行う)
def rbf(x1, x2, gamma):
tmp = x1 - x2
tmp2 = np.dot(tmp, tmp) * gamma
tmp3 = np.exp(-tmp2)
return tmp3
def rbfs(x1, xs, gamma, num_sv):
assert len(xs) == num_sv
res = []
for i in range(num_sv):
res.append(rbf(x1, xs[i], gamma))
return np.array(res)
gamma = 1 / (X_norm.shape[1]* X_norm[train_indices, :].var())
# take rbf (kind of mapping using exp) between data and model's support vector
# 非線形マッピングで特徴量をカーネル関数から作る作業。
tmp1 = rbfs(X_norm[0, :], regr.support_vectors_ , gamma, regr.support_vectors_.shape[0])
# use tmp1 (non-linear features) to map to target
# 非線形特徴量を後は線形回帰してクラシフィケーションを行う作業
tmp2 = np.dot(regr.dual_coef_, tmp1) + regr.intercept_
# 上の分解された作業とScikitLearnのpredict API で同じ結果が得られることを確認する作業
# just to compare the result with Scikitlearn API prediction
pre = regr.predict(X_norm[0:1, :])
pre.shape
このような処理を行うことになります。
ポイントは、上記の通り
- 特徴量空間へのマッピングを行う
- 特徴量空間の次元は、サポートベクターの数と等しくなること
- 特徴量空間へマップした後は線形回帰すること
となります。これでprediction関数と同じ結果が得られます。
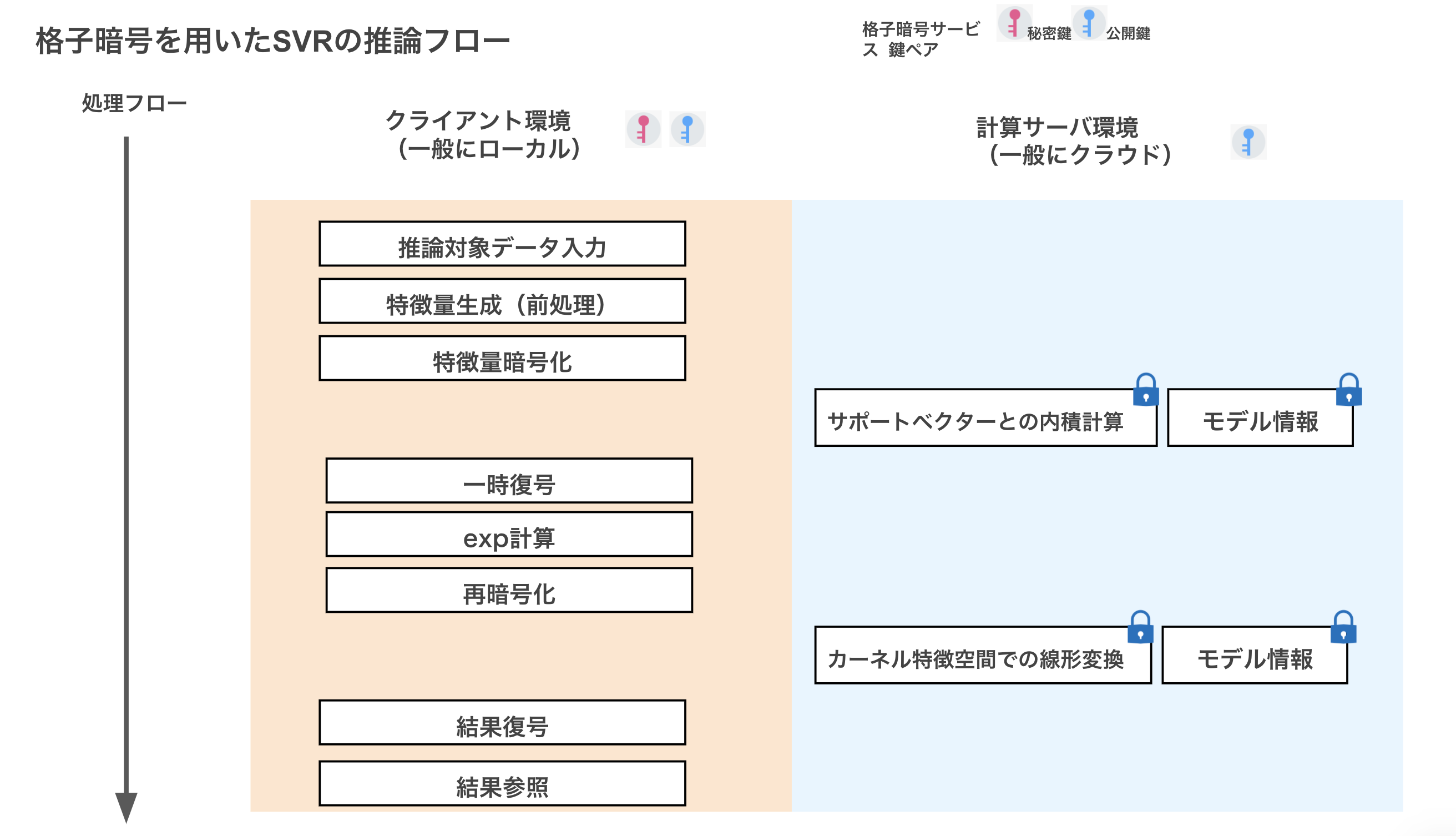
格子暗号を用いた処理フロー
今までいろいろとCKKS形式の格子暗号を用いた機械学習への応用を紹介してきました。
今回は簡単に処理フローを書くにとどめておきますが、SVRをCKKSを用いて処理しようとするとこのような処理フローとなります。
もちろん非線形関数をテイラー近似することで途中の通信は必要ではなくなりますし、
そこらへんは実装上の工夫やユーザの条件などにもよると思います。
まとめ
今回は、SVRについてまとめ、
SVRについて少し違う視点から捉えられたのではないかと思います。
いろいろなアルゴリズムがある機械学習ですが、
個人的にはいろいろな知識が繋がった瞬間というのはなにかテンションが上がる瞬間だなと思っています。
そのような捉え方ができるようにもう少し機会学習勉強してみようと思います。
今回はこの辺で。