概要
これは、前記事の続きになります。
量子耐性を持つと言われ、アメリカの標準技術機構NISTが数年のうちに安全性を評価し、標準化するという風に実際にもう動いている暗号は、大きく3つのカテゴリに分けられるようです。
- 符号理論に基づいた暗号
- 有限体上の多変数多項式の求解問題に基づいた暗号
- 格子理論に基づいた暗号
となりますが、このうちの3.格子理論に基づいた暗号のうち、
- NTRU暗号
- LWE(Ring-LWE)暗号
についてまとめていきます。
参考文献は、
小柴薫居さんの論文:多変数多項式環を用いた NTRU 暗号の拡張や、
NTRUのウィキペディア
id:u874072e藍屋えんさんのはてなブログの記事:暗号のしくみ~格子暗号編(NTRU)~
深瀬道晴さんの論文:格子と暗号に関する研究動向について
-暗号攻撃、格子暗号、完全準同型暗号
makoさんのブログ:SageMathでRing-LWEによる鍵共有
などです。日本には素晴らしい技術者、研究者の方がいらっしゃいますね。
NTRU暗号
NTRじゃないです。NTRUです。
格子暗号の中で唯一標準化されている暗号がこの NTRU暗号になります。

このときのfが秘密鍵になるのですが、fの逆元が暗号化の時にかけられているのを利用して、fを復号時にかけることで、埋め込まれた(足された)平文多項式の最近房の格子を求めることができます。
ここはやり方は違えど考え方は次のLWE形式とも同じです。
LWE(Ring-LWE)暗号
Learning with Error という問題を安全性の基点としており、Regevさんが提唱したのでRegev暗号とも呼ばれています。
LWE(Learning with Errors)問題とは、誤差を付加した多元連立一次方程式を解く問題です。 簡単に説明すると、Zq 上の誤差 e を付加した連立方程式について、行列 A,b が与えられたときに、秘密 s を求める問題です。
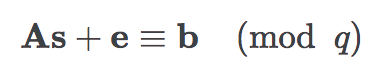
このとき、NTRUの時と同じように、イデアルをとる作業がこのsと掛け算をするときの作業であり、SVPもしくはCVPを求める問題に帰着させるためにノイズであるeを足したものが格子点として公開されます。
誤差がない場合の線型方程式はガウスの消去法などを用いて容易に解けますが、誤差が加わった線形方程式を効率的に解くアルゴリズムは現時点で見つかっていません。
LWE暗号に対して特筆すべきはその完全準同型性でしょう。LWE格子暗号では、素数qを法とする有限体上での演算のもとでの格子を考えます。 また、LWE格子暗号には暗号文のまま演算ができるという性質があり、このような性質を持つ暗号は準同型暗号と呼ばれます。
Ring-LWE
Ring-LWE(RLWE)問題とは、LWE問題を有限体上の多項式環に限定した問題です。 簡単に説明すると、以下の方程式で多項式 a(x),b(x) が与えられたとき、秘密の多項式 s(x) を求める問題です。
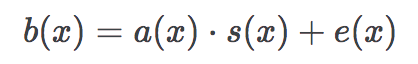
本来のLWE格子暗号は格子の次元をnとしたとき公開鍵の鍵長がO(n2)となります。 また暗号文の長さは平文のn倍になりますが、有限体の代わりに円分体の整数環上での演算を用いたRing-LWE(RLWE)格子暗号があります。 Ring-LWE格子暗号では、公開鍵の鍵長を数千bit程度にでき、また、複数ビットの平文を対応する多項式の係数で表すことにより暗号文の長さを格段に小さくできるため、多くの研究がこのRing-LWEベースの暗号に対して行われています。また、暗号文同士の演算が多項式演算のため、DFTおよびFFTを用いた計算の高速化を行うことができるのも利点です。
おわりに
準同型性や、Ring-LWEによる効率化を考えるとRing-LWEが注目を浴びて研究されているのもうなづけます。
次は格子だけでなく符号や多変数多項式に基づいた次世代暗号も調べてみたいです。
おわり。