概要
今回は量子コンピュータが台頭したあとに多項式時間で破られると言われている既存暗号とは違う数学的背景を持った、次世代型暗号とか、量子耐性暗号と呼ばれる暗号のうち、格子暗号について書いていきます。
量子耐性を持つと言われ、アメリカの標準技術機構NISTが数年のうちに安全性を評価し、標準化するという風に実際にもう動いている暗号は、大きく3つのカテゴリに分けられるようです。
- 符号理論に基づいた暗号
- 有限体上の多変数多項式の求解問題に基づいた暗号
- 格子理論に基づいた暗号
今回はこの中でも格子暗号に焦点をあてて書いていきますが、他も面白そうです。
ちなみに、格子暗号は量子耐性があるという観点だけではなく、それが完全準同型性をもつ暗号方式である(つまり、暗号化した後も足し算や掛け算などの計算可能)という利点もあります。(1.2 に関してもそうなのかはまだ勉強していません、すみません。)
このまとめ①では格子暗号の中でも歴史の古い
- Ajtai-Dwork暗号
- GGH (Goldreich, Goldwasser, Halevi)暗号
について簡単にまとめます。また、複雑な計算式に関してはわかりやすく書かれている参考文献へのリンクを貼っていきます。
まとめ②では
- NTRU暗号
- LWE(Ring-LWE)暗号
についてまとめていきますので、どうぞごらんください。
また、深瀬道晴さんの論文:格子と暗号に関する研究動向について
-暗号攻撃、格子暗号、完全準同型暗号が非常にわかりやすく、参考にさせていただきました。
格子暗号にもいろいろあるよ
こちらの、日本銀行の清藤武暢さんのスライドに各格子暗号についてとてもわかりやすくまとめられています。特に、27枚目のスライドが有用だと思ったので、それだけここに紹介させていただきます。

今回紹介するAjtai-Dwork暗号、ならびにGGH暗号はビット毎での暗号化になることと、セキュリティを達成する時に必要な次元数がNTRUやLWE形式に比べて膨大なため、あまり実用的では無いようです。しかしながら、格子理論を用いた初めての暗号がこのAjtai-Dwork暗号だったり、その次に出てきたのがGGH暗号だったりするので、それらの歴史を知っておくのは必ず有益だと考えます。
Ajtai-Dwork暗号
自分的には、Michael Hartmannさんの修士論文の42ページからの解説がとても分かり易かったです。
先ほども書いたように、このAD暗号は、初めて格子理論を暗号構成に応用したものです。何事も初めてというものは大事です。うん。
秘密鍵には超平面が使われ、公開鍵はその超平面を元にして超平面に近いベクトルになります。
面白いところは、平文をビットで書き直し、ビット毎に暗号化するのですが、0の時は公開鍵を用いて超平面に近いところに暗号化されるのに対し、1の時は完全にランダムのベクトルに暗号化されるところです。
論文を見ていても、ビット毎に暗号化する時の線形演算が多く、処理が重そうですね。
論文にも紹介されている通り、復号化するときに、1を0と復号してしまうエラーが大きく、そこをGoldreich, Goldwasser and Halevi が解決した論文を97年に出したようです。すごい。。
この暗号は、任意の暗号文が0であるか1であるかがわかるかどうかが、特殊な格子のSVPの最悪な場合を解くことと同じ、ということが示されているので、この特殊な格子のSVPを計算困難と仮定することで安全性を保証しているようです。
GGH暗号
GGH暗号は視覚的に比較的理解しやすい暗号です。視覚的にとてもわかりやすく書かれているのは、これまた日本銀行の清藤武暢さんのスライドであり、18ページになります。こちらも参考のため貼らせていただくと、
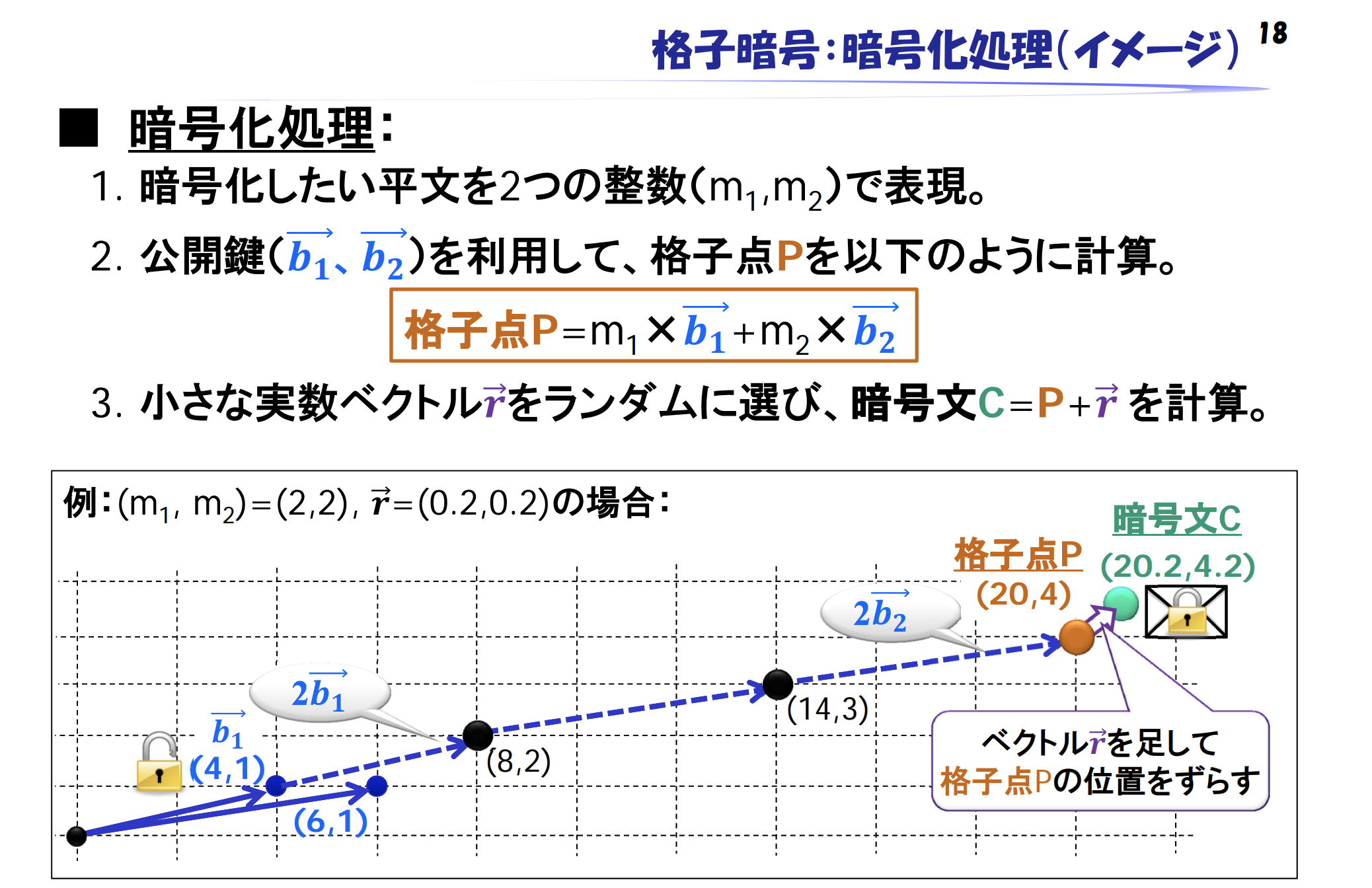
このスライドになります。
この暗号は、見てもわかる通りCVP問題を安全性の基点としているのですが、
視覚的にわかりやすいところは、暗号化したい平文を2つの整数で表現し、公開鍵(比較的直交していない格子の基底)と、ランダムノイズによって格子点を決定するということです。また、秘密鍵は(直交基底に近いもの)になるので、復号の時はそれらを用いて暗号文Cの最近点を計算し、暗号文を2変数の連立方程式によって求めるということになります。これはすごく直感的でわかりやすいです。
Nguyenらによる暗号攻撃
上で紹介した2つのAD, GGH暗号ですが、Nguyenによって実用的なセキュリティレベルで使用するには非常に非効率である(格子の次元がかなり大きく無いといけない)ということが示されています。それが理由で鍵長がかなり必要だ、という上のグラフになっています。
このNguyenという人、格子暗号の安全性を研究するコンテストTU DARMSTADT LATTICE CHALLENGEというコンテストでありえないくらい上位独占してるんですけど、どんな人なんでしょう。。。あと日本の研究者めっちゃすごいです!!
おわりに
結局参考文献を薄くまとめたものにはなってしまいますが、格子暗号の中にも歴史がありすごく面白いですね。また、格子暗号以外の符号や多変数多項式に基づいた次世代暗号についてもまとめてみたいです。
とりあえず次は、NTRUとLWE形式の格子暗号についてまとめます。
おわり。