LoginSignup
17
13

More than 3 years have passed since last update.

@kenmaro(Kentaro Mihara)inEAGLYS

暗号解説シリーズ　アメリカの頭脳を全て注ぎ込んだ２０世紀最強の暗号　「DES暗号」を解説！！

Posted at

DES (Data Encryption Standard)

今回は、共通鍵を用いたブロック暗号として、1970年代から現在まで世の中の安全な通信をになってきた、２０世紀最強の暗号「DES暗号」について解説します。

des.jpeg

この記事の流れ

  1. DESとは
    1. 共通鍵暗号
  2. DESが生まれた経緯
    1. 戦後からの歴史背景
  3. DESの基本設計
    1. 鍵の準備
    2. 入れ替え(転置)
    3. ファイステル(F)関数
    4. Sボックス
  4. DESの利点
    1. 組み込みやすさ
    2. 解読の難解さ
  5. DESの弱点
    1. 鍵長
  6. DESの改良型
    1. トリブルDES
  7. DESの次の暗号
    1. AES
    2. 公開鍵方式
    3. 次世代型暗号
  8. まとめ

1. DESとは

アメリカ合衆国の旧国家暗号規格、もしくはその規格で規格化されている共通鍵暗号である。
つまり、DES暗号はアメリカが戦後に国家として開発を推進し、IBMが英知を結集して作成した。また、NSAがその作成をサポートしたと言われている。

DESはブロック暗号の一種である。ブロック暗号とは入力データをある決まった長さのビット数ごとに切り分け、それらを順に暗号化し送信するものである。DESの場合は入力は64ビットであり、出力される暗号文も６４ビットとなっている。1976年国立標準局 (NBS) がアメリカ合衆国の公式連邦情報処理標準 (FIPS) として採用し、その後国際的に広く使われた。56ビットの鍵を使った共通鍵暗号を基盤としている。

1.1. 共通鍵暗号

DESの暗号化のやり方は「共通鍵暗号方式」と呼ばれるやり方である。
共通鍵暗号方式とは、暗号化と復号に「同じ鍵」を使用する暗号化方式のことであり、仕組みとしては古代のシーザー暗号もDES暗号も、暗号化する時と復号する時に「同じ鍵」を使う点では同じである。

対照的に、「公開鍵暗号方式」と呼ばれるものも存在する。この方式の場合、暗号化の時に使う公開鍵と、復号の時に用いる秘密鍵の２つを生成、運用することになるが、共通鍵方式の場合は、共通鍵１つに基づいている。

2. DESが生まれた経緯

2.1 戦後からの歴史背景

暗号といえば、それまでは軍事用として軍事活動を行うときの司令部と兵士達の間の通信を秘匿に行う目的で使われていた。
そのため、誰がどのような暗号を使用しているか、アルゴリズム自体もトップシークレットだった。(例えば、エニグマを使用していたドイツナチス軍など）

しかし戦後、コンピュータを多くの人が使うようになり、企業間での商取引等、インターネット上でやり取りするデータを安全に守ることが急務となった。そのために暗号アルゴリズムによりデータを秘匿しやりとりすることが考えられていた。

しかし、異なる企業間でやり取りをする際、お互いが別々の暗号方式を使い、アルゴリズムを公開しない場合は情報のやりとりなど不可能である。
そこで、IBMのHorst Feistelによって、「鍵を秘密」にし、「暗号アルゴリズムは公開する」DESが、暗号モジュールに関するセキュリティ要件の仕様を規定する米国連邦標準規格(FIPS 140)に採用され、米国国内基準となった。それから多くの国がこの基準に則り、DESを使うようになった。

3. DESの基本設計

DESは前述のようにブロック暗号であり、暗号化したい平文を６４ビットのブロックに分け、それぞれ暗号化のアルゴリズムに流していく。工程は、図に書かれているように、

  1. 平文をブロックの長さ（６４ビット長）に切り分ける
  2. ６４桁の数字を入れ替える（初期転置）
  3. ２からの入力を左右の３２ビット毎に分ける
  4. 右のグループには何も行わないが、左のグループにある計算（後述のファイステル関数）をし、それを足す（XOR演算とよばれる）
  5. 左と右のグループを入れ替える
  6. ３、４、５の工程（ラウンドと呼ばれる）を１６回繰り返す
  7. 出力の６４桁を入れ替える（最終転置）

となっている。

Screen Shot 2020-02-01 at 20.34.35.png

図１：　DESの基本構成

切り分けられた入力は上図に従い、64bit単位のデータに対してビット位置の変更（転置）やテーブル参照による置き換え（置換）、XOR演算、シフト、繰り返し処理などを組み合わせて、入力されたデータを可能な限り「かき混ぜる」という処理を繰り返すことによって暗号化される。
この方法では、上図の③に書かれているように、入力されたデータを2つ（もしくはそれ以上）に分け、一方に「暗号化関数（後述のファイステル関数）」による処理を適用してビットデータに変換措置を施す。この一回の操作（２つに切り分けて片方に関数を適用するステップ）をラウンドと呼ぶ。ラウンドが終了すると、切り分けられたデータの左右を入れ替えて同じ処理を繰り返す。この工程をDESは１６回繰り返す。これにより、入力データは完全に「かき混ぜ」られた状態になり、暗号文として出力される。

前述の通りDESは64bit（8bytes）単位でデータを暗号化するブロック暗号アルゴリズムである。したがって、入力や鍵データが64bitに満たない場合は、ゼロデータなどを追加して64bitにそろえてから処理を行うことに注意する。

3.1. 鍵の準備

初期鍵の生成

先ほどDESは５６ビット長の鍵を使うと説明したが、初期鍵は６４ビットからなっており、DESの初期設定として５６ビットの鍵を６４ビットの初期鍵から生成する準備が必要である。
この手順は、非常にシンプルであり、持ってきた初期鍵の8, 16, 24, 32, 40, 48, 56, 64桁目の数を単純に省く。

Screen Shot 2020-02-01 at 20.43.18.png

入ってきた６４桁の初期鍵を、緑で書かれた桁の部分を省くことでDESに必要な５６桁の鍵にしている。

ラウンド鍵の生成

先述のとおり、DESではラウンドを１６回繰り返す。各ラウンドでは④の操作（ファイステル関数を左のグループに適用）があるが、その操作に鍵を使用する。DESでは、その時に使用する鍵を各ラウンドごとに変えている。その１６個の鍵を初期鍵から生成する方法は、「Key Mixing」と呼ばれる。また、ラウンド鍵は初期鍵が５６ビットなのに対して、４８ビットである。
Key Mixing は以下の流れで行われる。

  1. シフト演算: ５６ビットの鍵を、左右２つのグループ（それぞれ２８ビット）に分ける。各グループが、した図にしたがって左にシフト演算される。このとき、ラウンド１、２、９、１６で使用される鍵は左に「１」シフトされる。他のラウンド用の鍵は、左に「２」シフトされる。いくつ左右に分割された鍵がシフトされるかは、下図にまとめられている。

（シフト演算は、[1,2,3]を左に１つシフトすると、[2,3,1]となるような演算のこと。）

Screen Shot 2020-02-01 at 20.49.33.png

2.　縮小転置: シフト演算の後は、５６ビットある鍵から４８ビットを抽出する作業がある。これは下図に従う。下図のテーブルは$12 \times 4 = 48$個の数で構成されているが、これは、シフトされた後の１４番目にある数が１番目に動かされ、１７番目にある数は２番目に動かされ、・・・・という作業を表している。ここで、もともと５６個あった鍵長だったが、この作業より４６個に縮小していることがわかる。すなわち、８個の数はこの表には入っていない。例えば、７という数字はこの表には入っていないため、シフト演算後に７番目にあった数はラウンド鍵には使われず、除去されている。

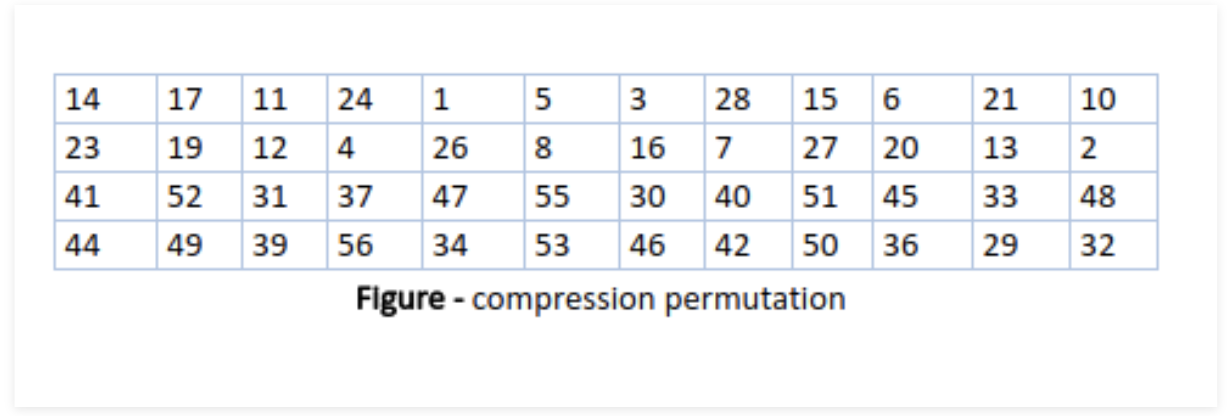
Screen Shot 2020-02-01 at 20.51.10.png

この縮小転置の作業により、初期鍵の異なる部分のビット情報が、各ラウンド毎に使い分けられている。この作業がDESの解読を困難にしている。

3.2. 初期転置

鍵が準備できたので、ここからは入力に対しての工程である。図１の②に相当する作業が、この初期転置である。

この初期転置は、ラウンドに入る前に行われる、入力ビットの入れ替え作業である。これは下図のテーブルに従う。先ほどの縮小転置とは異なり、この初期転置では６４ビットの入力に対して６４ビットのものが出力され、次に続くラウンドへの入力となる。表は$16\times16 = 64$であり、例えば、入力の５８番目にあった数が出力の１番目の数になり、５０番目にあった数が２番目になり、・・・・　というように入れ替えられる。

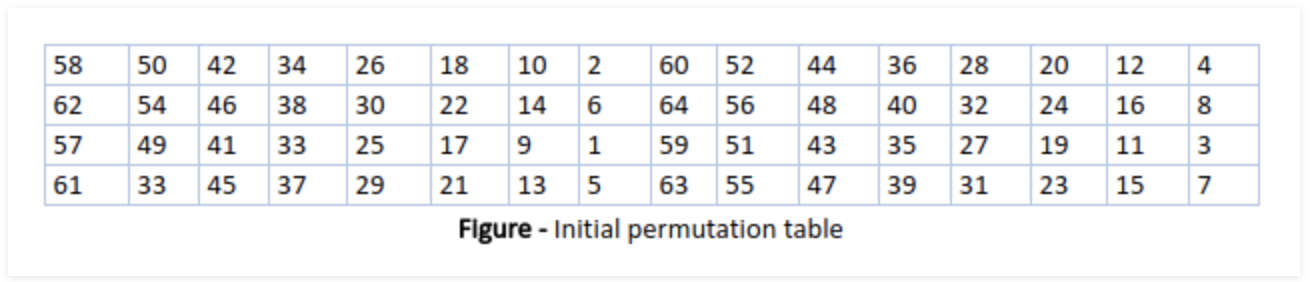
Screen Shot 2020-02-02 at 16.18.47.png

この作業が完了すると、ラウンドに入る前に入力は左右２つのグループに分けられる。入力は６４ビットなので、左右に分けられたグループはそれぞれ３２ビットの入力として次のファイステル関数へと入っていく。

3.3. ファイステル(F)関数

ファイステル(F)関数

ファイステル関数はブロックの右半分（32ビット）を入力として受け取り、出力を左半分（32ビット）にXOR加算する関数である。図式すると以下のようになる。
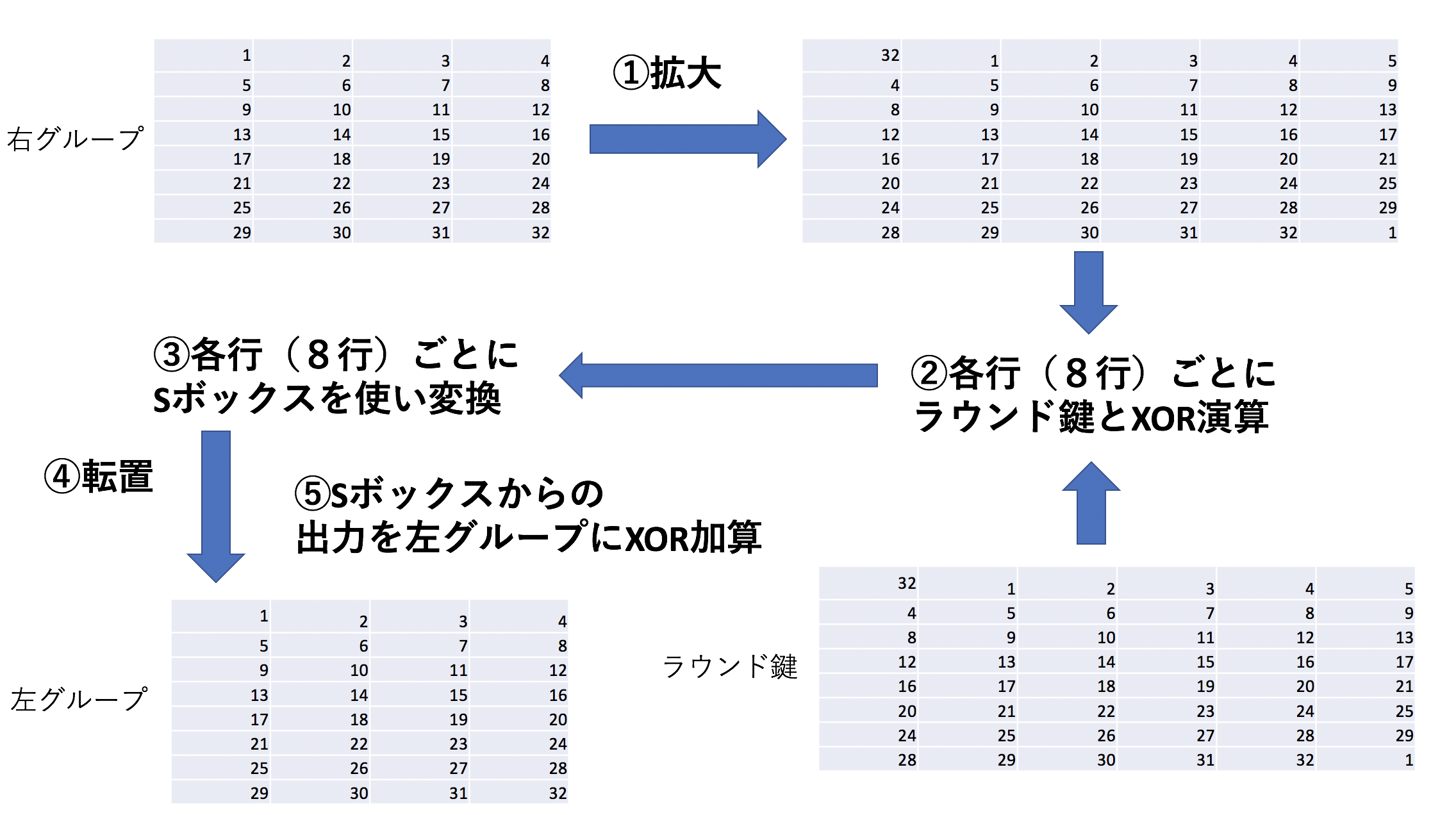
Screen Shot 2020-02-02 at 18.45.33.png

  1. 拡大
  2. 各行毎にラウンド鍵をXOR加算
  3. Sボックスによる非線型変換
  4. Sボックスからの出力を転置
  5. 結果を左グループにXOR加算

拡大

32ビットを48ビットに拡張する。図では ①で示されている部分である。入力のうち半分のビットの複製をビット列に加える。出力は6ビットの（行）が8個あり、そのうち真ん中の4ビットは入力の対応する4ビットの部分と同じで、両端のビットは入力上で隣接する部分のビットの複製である。

各行毎にラウンド鍵をXOR加算

ラウンド鍵と、①で拡大された入力を各行でXOR演算する。

Sボックスによる非線型変換

②からの出力は８行６列のテーブルになっているが、各行毎に８個あるSボックスに入れる。つまり、１行目はSボックス１に入り、２行目はSボックス２に入り、・・・・・　となる。
後述のSボックスは各行の６ビットを４ビットに変換して出力するため、③の出力は８行４列のテーブルになる。

Sボックスからの出力を転置

この転置作業は、Sボックスからの８行４列のテーブルに対し、行を転置する。この作業により、各Sボックスの出力が次のラウンドでSボックスに展開されるとき、6個の異なるSボックスに分散するよう並べ替える。

結果を左グループにXOR加算

④の結果出てきた８行４列のテーブルを、左グループにXOR加算する。

3.4 Sボックス

先述のように、②でラウンド鍵を混ぜた後、6ビットずつに分けてSボックス (substitution box) に入力する。8個のSボックスは入力の6ビットから4ビットの出力を生成し、このときルックアップテーブルの形で提供される非線形な変換を行う。Sボックスは８個あり、ナンバリングされている。Sボックスを全て書いたものは以下の表である。
Screen Shot 2020-02-01 at 21.01.30.png

ここではこのうちSボックス１を見てみる。
Screen Shot 2020-02-02 at 18.54.23.png

各Sボックスへの割り当て

②からの出力は８行あるため、各行が各Sボックスに入力される。Sボックス１に入力されるものは１行目であり、Sボックス２に入力されるものは２行目、・・・・・　と続いていく。

ボックス内の参照先決定

Screen Shot 2020-02-02 at 19.01.29.png

例えば入力が$010001$だった場合、参照後の出力は$10$となる。

各行は６つのビットからなっている。このうち１番目と６番目のビットにより、Sボックスのどの行を参照するかを決定する。次に、２、３、４、５番目のビットにより、どの列を参照するかを決定する。
例えば、入力が$010001$の時、１番目と６番目は$01$なので、Sボックスの1と書かれた行を参照することが決定。次に、２、３、４、５番目が$1000$であるため、Sボックスの1000と書かれた列を参照することを決定する。したがって、参照された後の出力は$10$となる。

SボックスがDESの安全性の根幹であり、これがないと暗号は線形なものとなって容易に破ることができることになる。

ただ、このSボックスがなぜこうデザインされているのか疑問に持った人も多いのではないだろうか。これではあまりにもブラックボックスすぎて、なぜこれで安全性が担保されるのか全くわからない。
ただし、このSボックスのデザインはとても秀逸に行われている。例えば、もしSボックス３とSボックス７が入れ替わったデザインの場合、極端に弱い暗号になってしまうことが知られている。

同じように、DESが発表された時にこのSボックスに対していろいろな議論が交わされた。どうやってこれが決められたのかが謎だったため、NSAがIBMに介入し、NSAだけが解読できる工夫をSボックスに施したのではないか、という陰謀論が囁かれたのである。以下はウィキペディアから取ってきたものだが、とても面白いので読んでみてほしい。

NSAの設計への関与

1975年3月17日、規格案としてのDESが Federal Register に発表された。そしてコメントが募集され、翌年には2回ワークショップを開催してこの規格案について議論した。各所から様々な批判が寄せられた。中には公開鍵暗号の先駆者であるマーティン・ヘルマンとホイットフィールド・ディフィーの批判があり、鍵長が短いという点と謎めいた「Sボックス」がNSAによる不適切な干渉を意味しているのではないかと指摘した。

それは、このアルゴリズムを諜報機関が密かに弱め、その諜報機関だけが暗号化されたメッセージを容易に解読できるようにしたのではないかという疑いが持たれたのである。アラン・コンハイム（DES設計者の1人）はそれについて「我々はSボックスをワシントンに送った。戻ってきたものは送ったものとは全く異なっていた」と述べた。アメリカ合衆国上院諜報特別委員会がNSAの行為に不適切な干渉があったかどうかを調査した。調査結果の公開された要約には次のように書かれている。

「DESの開発において、NSAはIBMに対して鍵長が短くても大丈夫だと納得させ、Sボックスの開発を間接的に支援し、最終的なDESアルゴリズムが統計学的にも数学的にも考えられる最高のものだと保証した」
しかし、同時に次のようなことも判明している。

「NSAはいかなる形でもアルゴリズムの設計を改変していない。IBMはこのアルゴリズムを発明・設計し、関連する設計上の意思決定は全てIBMが行い、鍵長もDESのあらゆる商用の用途にとって十分な長さとして決定した」
DES設計チームのウォルト・タックマンは「我々はIBM内でIBMの人員だけでDESアルゴリズム全体を開発した。NSAに命じられて変更した部分は1つもない」と述べた。

4. DESの利点

4.1. 組み込みやすさ

DESのアルゴリズムを図にすると、かなり複雑な処理を行っているように見える。だが実際には、ハードウエアとして実装するなら簡単なビット演算（XOR演算）とシフト、テーブル参照などだけで処理できるため、非常に高速に処理できる。

4.2. 解読の難解さ

DESが開発された後、DESの解読を目的とした研究が盛んに行われるなか、DESはその堅牢性を崩すことがなかった。様々な解読法が研究される中で、DESを設計したIBMとNSAの設計の崇高さが露見していった。

それを知るために、ここでは全数探索法と、ショートカット法について少しだけ言及した後、ウィキペディアからのエピソードを紹介する。

全数探索法とショートカット法

鍵の総当たりで解読する方法を全数探索法や、総当たり法と呼ぶ。全数探索法は、暗号のアルゴリズムにかかわらず任意の暗号に対して適用できるが、鍵のビット長が$n$ のとき、$2^n$の試行回数が必要である。つまり、ハードウェアの計算能力による。総当たり法では、平文と暗号文のペアが少数与えられた時に、鍵の候補を総当たりで試す。したがって、鍵のビット数は、これからの計算機能力の進化を考えても十分に探索し尽くすことができないと思われる長さに設定される。これに対し、暗号アルゴリズムの内部構造の知識を生かし、全数探索法より少ない試行回数で暗号の解読を目指す方法を、ショートカット法という。

IBMとNSAの驚くべき策略

１９９０年、エリ・ビハムとアディ・シャミア（RSAのS）が差分解読法を独自に発見して公表した。差分解読法はブロック暗号を破る汎用技法である。DESのSボックスは無作為に選ばれた場合よりもこの攻撃法にずっと抵抗力があり、IBMが1970年代にこの攻撃法を知っていた（！！！）ことを強く示唆していた。1994年、ドン・コッパースミスがSボックスの元々の設計基準について一部を公表したことで、それが裏付けられた。

スティーブン・レビーによれば、IBMでは1974年に差分解読法を発見していたが、NSAがそれを秘密にするよう要請していたという。コッパースミスはIBMの方針について「（差分解読法）は非常に強力なツールであり、様々な方式に応用でき、これを公にすると国家の安全に悪い影響を及ぼすことが懸念された」と述べている。

このように、DESは当時のアメリカの頭脳全てをつぎ込み生み出された、２０世紀最強の暗号だったのである。

5. DESの弱点

5.1. 鍵長

２０世紀の最後から２１世紀にかけて、コンピューターの計算能力の進化には目覚ましい発展があった。それに伴い、DESは今では多くの用途において安全ではないと見なされている。これは主に56ビットという鍵長が短すぎることに起因する。

1999年1月、distributed.netと電子フロンティア財団は共同で、22時間15分でDESの鍵を破ったことを公表した。これは前述の総当たり法を使った例であり、彼らはDES解読用のハードウェアを、ネットワークでつないだ複数の計算機で並列で走らせた。それによりこの２２時間という驚異的なタイムでDESを破ったのだった。DES暗号を破るコンテストも開催され、条件次第では数秒で暗号を破ることが可能であることが明らかとなるに至り、新しい標準暗号の必要性が決定的となった。

6. DESの改良型

もう1つの理論的攻撃法である線形解読法は1994年に公表された。上記の通り1998年には総当り攻撃で実用的な時間でDESを破れることが実証され、アルゴリズムの更新の必要性が高まった。1990年代後半になると、総当たり攻撃による解読の成功例が報告されるようになった。そこで1998年に登場したのが、DESを強化した3DESだ。

6.1. トリブルDES

トリプルDES（トリプルデス、英語: Triple DES、3DES）とは、共通鍵ブロック暗号であるDESを3回施す暗号アルゴリズム。正式名称はTriple Data Encryption Algorithm(TDEA、Triple DEA)。時代の流れに伴い、鍵長56ビットのDESでは総当たり攻撃への耐性が低くなったことから、これを補う目的で考案された。
3DESは、DESを「暗号」「復号」「暗号」の順で3回実行することで暗号強度を高める。実装が比較的容易なことから、3DESはクレジットカードの暗号化など、金融関連で幅広く利用されてきた。

ここで、3つの鍵{k1,k2,k3}を使うトリプルDES (-EEE) が、1つの鍵k4でDESを行う場合よりも安全性が向上するかが問題となるのだが、DESを多段にすることで鍵空間は拡大できることが示され、トリプルDESの優位性が証明されている。

トリプルDESの種類

トリプルDESは前述の通りDESの操作を３回繰り返すことで暗号強度を高める手法であるが、その３回に使う鍵をどう選ぶかで３種類に分類される。各種類により、鍵空間の大きさが異なる。分類方法とその鍵空間の大きさは以下である。

  1. k1, k2, k3 すべてが異なる場合
  2. k1 と k2 が異なり、k3 = k1 の場合
  3. k1 = k2 = k3の場合

k1, k2, k3 すべてが異なる場合

3 × 56 = 168ビットの鍵長となるが、既知の攻撃法が存在するため実質的な暗号強度は112ビットとなる。3TDEA、3-key 3DES などと呼ばれる。

k1 と k2 が異なり、k3 = k1 の場合

2 × 56 = 112ビットの鍵長となるが、既知の攻撃法が存在するため実質的な暗号強度は80ビットとなる。中間一致攻撃への耐性があるため、単純にDESで2回暗号化するよりは安全である。2TDEA、2-key 3DES などと呼ばれる。

k1 = k2 = k3の場合

DESと同じであり、56ビットの鍵長を持つ。このオプションにより、トリプルDESはDESに対して上位互換性を持つ（DESによって暗号化された文章をトリプルDESで復号できる。）

7. DESの次の暗号

さらばDES暗号、2023年終了へカウントダウン
https://tech.nikkeibp.co.jp/atcl/nxt/column/18/00001/00986/
米国立標準技術研究所（NIST）が2018年7月19日、DESを強化した暗号アルゴリズムである「3DES」について、これから開発するアプリケーションで採用することをやめ、2023年以降は使用を禁止することを提案したからだ。

前述の通り、コンピューターの計算スペックの向上により、５６ビットの鍵長であるDESが全数探索法で簡単に破られてしまう未来が近いことがわかっている。そこで、アルゴリズムの更新の必要性が高まり、DESにとって変わる次の標準暗号アルゴリズムを、米国政府は募集し次の暗号アルゴリズムを選定した。

7.1. AES

2001年にAESが米国政府の標準暗号アルゴリズムとなり、DESはより安全なAESに取って代わられた。

その大きな強みは鍵長を選択できることにある。暗号アルゴリズムを破るのにかかる時間は、通信の保護に使われる鍵の長さに依存する。AESでは128bit、192bit、256bitの長さの鍵を選べる。それぞれDESが使用する56bitの鍵と比べて長く、暗号強度を高めやすい。AESの方がDESより高速に暗号化できる点でも優れている。そのため低遅延や高スループットが要求されるアプリケーション、ファームウェア、ハードウェアでの利用に適している。

7.2. 公開鍵方式

「共通鍵暗号」の最大の問題は、他人に知られてはいけない鍵の配送をどのように行うかであった。
2000年以上人類を悩ませていたこの問題を解決に導いた発明が、1976年ホイットフィールド・デフィーとマーティン・ヘルマン、ラルフ・マークルによって考案・発表された「公開鍵暗号」である。そしてDESが採用された1977年には、この理論を実装した「RSA」暗号が登場した。

7.3. 次世代型暗号

次世代型暗号として、格子暗号をはじめとした高機能暗号の研究も盛んに行われている。
次世代暗号については以前に少しだけまとめているので、興味のある方はぜひ量子耐性をもつ暗号まとめ①をご覧いただきたい。

8. まとめ

今回は２０世紀最後から現在にかけて通信の安全性に大きく貢献した、「DES暗号」について解説した。
DESの開発により、解読法の研究など多くの研究が進み、社会的技術としての貢献とともに、暗号の学術的にも比類なき貢献がなされた。
多くの歴史的背景や、陰謀論などを含めながら学習することでとても面白かった。
次は今回は深掘りできなかったショートカット法である、線形解読法や差分解読法について学習してみたい。

もしこの記事で暗号について興味を持っていただけた方は、「いいね」や「コメント」をよろしくお願いいたします！！

おわり。

参考文献

17
13
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
17
13