ニューラルネットの積分表示と輸送経路問題

概要

ニューラルネットの積分表示によってニューラルネットの幾何学的性質や解析的性質が調べられる。
また、深層ニューラルネットによって層の浅いネットワークに比べて何が良くなるのかを調べる際、輸送経路問題を用いた輸送写像を用いることで、複数層になることで生まれる積分表現の入れ子問題を解決することができる。

以下が素晴らしいので参照していただきたい。

• ニューラルネットの積分表現理論――リッジレット変換とオラクルサンプリングによる3層パーセプトロンの学習の数値実験
• 深層ニューラルネット理論の近況 園田 翔 (理研 AIP 深層学習理論チーム)

自分の知識がなさすぎるので、これからこれを理解するための記事を出していけたらと思います。すみません。

積分表示

積分表現理論は、 １９９０年代に開発された浅いNNの理論である。積分表現理論は，浅いNNを積分表現にして、関数解析ないし調和解析を用いてNNの関数近似能力を調べる理論である。

ニューラルネットを次のような式で書いたとする。

$(a_j,b_j,c_j) ∈ R_m \times R \times C$であり、xは(a_j,b_j,c_j)によってパラメータづけされた関数$g$で表されている。

ここで、次の関数で表される関数をニューラルネットの積分表現という。

積分表現は，$(a, b) ∈ R_m \times R $で添字付けられた連続無限個の中間層素子 $\sigma (a · x − b)$ を足し合わせた浅いNNとみなせる。
連続化に伴い，出力係数 $c_j $は係数関数 $\gamma (a,b)$になる。

NN を積分表現にするメリットはいくつもあるが，最も重要なことは，パラメータが線形になることである。元の NN では非線形関数 $\sigma$ の中にある隠れ層パラメータ $(a_j , b_j )$ が非線形パラメータとなっていたが，積分表現では隠れ層パラメータが積分消去されるためである。
この時、積分表示は、添字付けられた連続無限個の中間層素子 $\sigma(a · x − b)$ を足し合わせた浅いNNとみなせる。すなわち、連続無限個の中間層素子によって、任意の関数を表す浅いニューラルネットワークを作っている。

通常の浅いNN(左)と積分表現NN(右)。積分表現では中間層素子が連続無限個足されている。

例えばデータセット $D = { (x_i,y_i) | y_i = f(x_i) = sin(2 \pi x), x_i ∈
{ −1.00,−0.99,...,0.99,1.00 } }$
に対して1000体の浅いニューラルネットをバックプロパゲーションで学習させて、学習された $(a, b) ∈ R_m \times R $をプロットしたものは以下になる。

つまり、学習によってガウシアン分布で始まったランダム分布は偏った分布になる。言い換えると、空間にはよく使われる場所とそうでない場所があるということである。
この偏りは学習したい関数 $f(x)=sin(2 \pi x)$にもちろん依存しているであろうことが予想できる。

ここで、中間層素子の個数を無限大にして、任意の関数の近似を、浅いニューラルネットワークで行いたいわけですが、デルタ関数を使って無理やり


と書き、これを関数 T(a,b) の η(x) による 双対リッジレット変換(dual ridgelet transform)と呼ぶ。リッジレット変換 R[f ](a, b) のスペクトルの散布図は、

概ねスペクトルの絶対値が大きい場所に，学習済パラメータが分布していることが分かる。この積分表示されたパラメータ空間の分布の偏りと、リッジレット変換で得られたスペクトルの分布が類似していることは、数学的にも証明されている。

輸送写像

輸送経路問題については調べていただきたいが、
このペーパーなどもぜひみていただきたい。

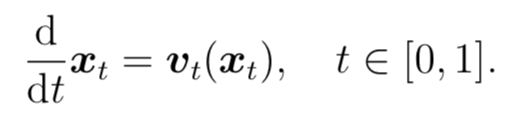
上の式が定めるような連続力学系 $g_t→s :R_m →R_m$ をニューラルネットのフロー表現という。フロー表現にすることで，深層 NN の中間写像の解析を輸送軌道の解析に転嫁できる。フロー表現を，$t ∈ [0, 1] $ で添字付けられた無限個の輸送写像 $g_t→t+0 $を合成して得られ る深層 NN とみなすことで、有限層の深層ニューラルネットが次の図のように得られる。

ここで、Euler法などの近似を用いてODEを解くことは、離散的な有限層の深層ニューラルネットを得ることに繋がる。

簡単なまとめ

結局参考文献をリンクするだけの記事になってはしまったが、ニューラルネットのダイナミクスを、積分表現によって考察できる。また、リッジレット変換と輸送理論に基づいて深層ニューラルネットの中間層をODEを用いて表現し、ニューラルネットのホワイトボックス化を進めようとする研究があることがとても面白く感じた。色々もっと勉強したい。

おわり。