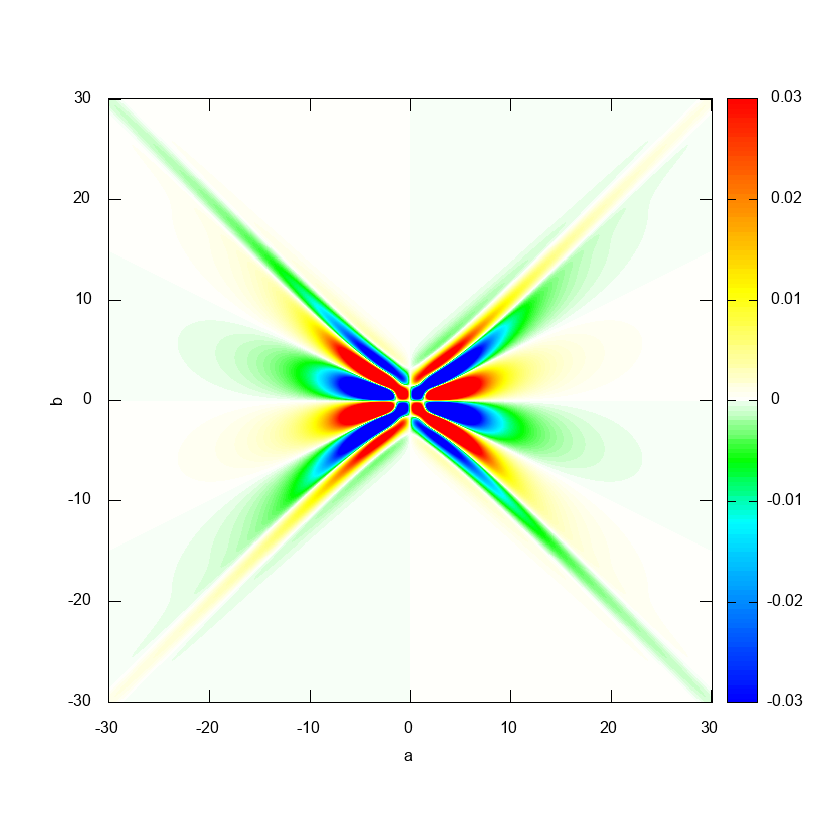ニューラルネットの積分表現理論――リッジレット変換とオラクルサンプリングによる3層パーセプトロンの学習の数値実験

概要

園田翔『深層ニューラルネットの積分表現理論』[3]という論文の中で「(浅い)ニューラルネットワークがしていることは 双対リッジレット変換 (の離散化)である」ということが解説されています．
この論文では入力を一般の $m$ 次元にとり，活性化関数として ReLU やシグモイド関数を含む超関数のクラスに対して結果を与えています．が，そのぶんとても難しいです． ¹

そういうわけで，本稿では上の論文で提案されている「オラクルサンプリング」という手法を

• 活性化関数として Gauss 核 $\eta(x) = \exp(-x^2/2)$ (急減少関数)を用い，
• $m = 1$ 次元の場合に限って

解説し，さらにその数値実験をしようと思います．

(本稿を読む前に園田先生のスライド[2]に目を通しておくことをおすすめします．)

使ったもの

• Python 3.6.0
• Chainer v3.1.0
• Octave 4.2.2
• Gnuplot 5.2

ソースコード

導入

今回利用するモデルは次の浅いニューラルネット(3層パーセプトロン)です:

\begin{align*}
g&\colon \mathbb{R}^m \to \mathbb{R},\\
g(\mathbf{x}) &= \sum_{j=1}^J c_j \eta(\mathbf{a}_j \cdot \mathbf{x} - b_j).
\end{align*}

ここで $J$ は正の整数， $\eta(x) = \exp(-x^2/2)$ は活性化関数， $\mathbf{x}, \mathbf{a}_j \in \mathbb{R}^m$ は $m$ 次元のベクトル， $b_j, c_j \in \mathbb{R}$ は実数， $\cdot$ は $\mathbb{R}^m$ の通常の内積です．
このモデルを使って，閉区間 $[-1, 1]$ 上の実数値関数 $f(x) = \sin(2\pi x)$ を学習することを考えてみましょう．
この場合入力は $m = 1$ 次元なので上のモデルは $g(x) = \sum_{j = 1}^J c_j \eta(a_j x - b_j)$ となります．

このニューラルネット $g$ のトレーニングを1回行うと，結果として重みとバイアスの $J$ 個の組 $(a_j, b_j)_{j=1}^J$ が出来上がります(ここでは $c_j$ は一旦無視します)．
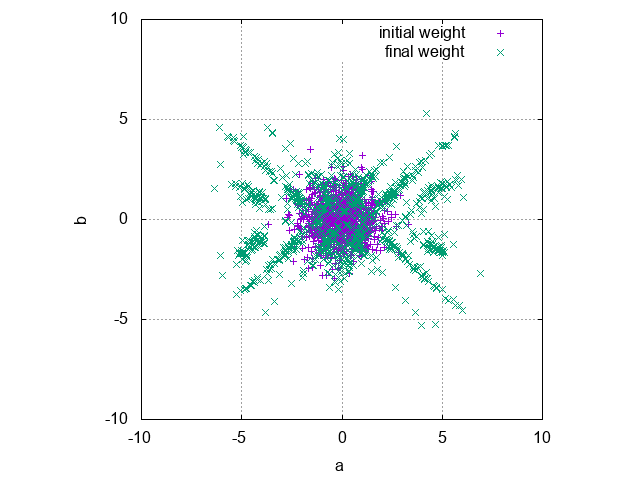
このトレーニングをたくさん繰り返して，バイアスと重みの組 $(a_j, b_j)$ を平面にプロットしてみましょう．
何が起こるでしょうか？

中間素子の個数を　$J = 10$ として，1000 epoch のトレーニングを 100 回実行し，学習後の各中間素子の重みとバイアスの組 $(a_j, b_j)$ をプロットしたものが以下です(中間素子が $J = 10$ 個のネットワークが $\times 100$ 個なので，全部で $1000$ 個の点がプロットされます)．
ライブラリは　Chainer を用い， optimizer は(なんとなく) Adam を使用しました．

図から， $ab$-平面において，パラメーターの「使われやすさ」に偏りがあるのがわかります．
この偏りは学習したい関数 $f(x) = \sin(2\pi x)$ に依存しているであろうことは想像に難くありません．
このことから，「学習したい関数 $f(x)$ から，『パラメーターの使われやすさ』を表す分布を直接計算し，使われやすいものをあらかじめ重み・バイアスの初期値とすることでバックプロパゲーションによる学習を有利に開始できるのではないか？」ということが予想されます．
実際，これが上の論文における手法の核心です．

ニューラルネットの連続化

先程のニューラルネットにおいて，中間素子の個数を増やせば増やすほど近似能力は高くなります．
実際，任意の「良い」関数は3層パーセプトロンで「近似」できることが知られています． ²

ならば，中間層の素子の個数 $J$ を無限大にすれば究極の近似能力が得られそうです．
$g$ の定義において $J \to \infty$ としたいわけですが，そのままでは考えにくいので， 少し無理やりですがデルタ関数を用いて和を積分に書き換えてみます．

\begin{align*}
g(\mathbf{x}) &= \sum_{j = 1}^J c_j \eta(\mathbf{a}_j \cdot \mathbf{x} - b_j)\\
&= \int_{\mathbb{R}^m \times \mathbb{R}} \left(\sum_{j = 1}^J \delta(\mathbf{a} - \mathbf{a}_j) \delta(b - b_j) c_j\right) \eta(\mathbf{a} \cdot \mathbf{x} - b) \, d\mathbf{a} \, db.
\end{align*}

よって関数 $T\colon \mathbb{R}^m \times \mathbb{R} \to \mathbb{R}$ を $T(\mathbf{a}_j, b_j) = \sum_{j = 1}^J \delta(\mathbf{a} - \mathbf{a}_j) \delta(b - b_j) c_j$ と定義することで $g(\mathbf{x})$は

(\mathcal{R}^\dagger_\eta T)(\mathbf{x}) = \int_{\mathbb{R}^m \times \mathbb{R}} T(\mathbf{a}, b) \eta(\mathbf{a} \cdot \mathbf{x} - b) \, d\mathbf{a} \, db

と書き直せます．これが関数 $T(\mathbf{a}, b)$ の $\eta(x)$ による 双対リッジレット変換(dual ridgelet transform) $(\mathcal{R}^\dagger_\eta T)(\mathbf{x})$ です． ³

双対リッジレット変換は積分変換の一種なわけですが， Fourier 変換や Laplace 変換と同様の「逆変換」が存在します．
それが次に示す，関数 $f(\mathbf{x})$ の $\psi(x)$ による リッジレット変換(ridgelet transform) $(\mathcal{R}_\psi f)(\mathbf{a}, b)$ です: ⁴

(\mathcal{R}_\psi f)(\mathbf{a}, b) = \int_{\mathbb{R}^m} f(\mathbf{x}) \psi(\mathbf{a} \cdot \mathbf{x} - b) \, d\mathbf{x}.

リッジレット変換と双対リッジレット変換は互いに逆の関係にあるので，以下の 再構成公式 が成り立ちます．

(\mathcal{R}^\dagger_\eta \mathcal{R}_\psi f)(\mathbf{x}) = f(\mathbf{x}) \quad \text{a.e.}

ただし， $\eta$　と $\psi$ は何でもよいわけではなく，以下の 許容条件 を満たしていなければなりません． ⁵

K_{\eta, \psi} = (2\pi)^{m - 1} \int_{-\infty}^\infty \frac{\overline{\hat{\psi}(\zeta)} \hat{\eta}(\zeta)}{\lvert \zeta \rvert^m} \, d\zeta = 1.

ここで $\hat{\psi}(\zeta)$ は $\psi(x)$ の Fourier 変換です．

本稿では活性化関数として Gauss 核 $\eta(x) = \exp(-x^2/2)$ を用いることに決めていたので，上の許容条件を満たすような $\psi(x)$ を求めなければなりません．
次節ではこの $\psi(x)$ としてどのようなものがとれるかを考えていきます．

数学的準備

まず，フーリエ変換(1次元)の復習から始めることにします．

$f, F\colon \mathbb{R} \to \mathbb{R}$ を実関数とするとき， $f$ の Fourier 変換と $F$ の逆 Fourier 変換をそれぞれ

\begin{align*}
(\mathcal{F}f)(\xi) &= \hat{f}(\xi) = \int_{-\infty}^\infty f(x)e^{-ix\xi} \,dx,\\
(\mathcal{F}^{-1}F)(x) &= \check{F}(x) = \frac{1}{2\pi} \int_{-\infty}^\infty F(\xi)e^{ix\xi} \,d\xi
\end{align*}

と定義します($i$ は虚数単位 $\sqrt{-1}$)．⁶

このとき， Fourier 反転公式

\check{\hat{f}}(x) = f(x)

が成り立ちます．また，微分の Fourier 変換は

\widehat{\frac{df}{dx}}(\xi) = i\xi \cdot \hat{f}(\xi)

のように求められるのでした．
また Gauss 核 $G(x) = \exp(-x^2/2) , (= \eta(x))$ とおくと

\hat{G}(\xi) = \sqrt{2\pi} \exp(-\xi^2/2) = \sqrt{2\pi} G(\xi)

となります．
ReLU やシグモイド関数は無限遠で消えないため，通常の関数の意味での Fourier 変換が存在しません(積分が発散してしまうため)．
そのため本稿では活性化関数として Gauss 核を用いています．
Gauss 核は急減少関数であるため　Fourier 変換が通常の関数として存在し，超関数を持ち出す必要がないという(初学者が勉強する上での)利点があります．
また上の式からわかるように Gauss 核は Fourier 変換の手計算が簡単であるという長所があります．

さて， $m = 1$ の場合の許容条件

K_{G, \psi} = \int_{-\infty}^\infty \frac{\overline{\hat{\psi}(\zeta)} \sqrt{2\pi} G(\zeta)}{\lvert \zeta \rvert} \, d\zeta = 1

を満たすような $\psi(x)$ を見つけるにはどうすればよいでしょうか．
なにもないところから考えるのは難しいので， $G(x)$ に手を加えて $\psi(x)$ を作ることにしましょう．
$K_{G, \psi}$ の分母には絶対値 $\lvert \zeta \rvert$ が含まれていますが，絶対値を含む積分というのは手計算が面倒なので，なんとか避けたいところです．
$\psi(x) = G'(x)$ とおけば $\hat{\psi}(\xi) = i\xi \hat{G}(\xi)$ となって $\xi$ が前に出てくるのですが，それでも $\xi$ の符号 $\operatorname{sgn} \xi$ は打ち消されずに残ってしまいます．
この状況を打破するために，多少天下り的ですが， Hilbert 変換というものを導入します．
Hilbert 変換 $\mathcal{H}$ は関数 $f$ に作用させてから Fourier 変換を施すと

\widehat{\mathcal{H}f}(\xi) = (\operatorname{sgn} \xi) \cdot \hat{f}(\xi)

という変換法則を満たします．まさにこれが欲しかった変換です．
よって， $\psi(x) = (\mathcal{H}G')(x)$ とおけば $\hat{\psi}(x) = i\xi (\operatorname{sgn} \xi) \cdot \hat{G}(\xi) = i\lvert \xi \rvert \hat{G}(\xi)$ となり， $\lvert \xi \rvert$ を打ち消すことができます． ⁷

(\Lambda f)(x) = \frac{1}{i} \left(\frac{d}{dx} \mathcal{H} f\right)(x)

を 逆投影フィルタ といいます．つまり

\widehat{\Lambda f}(\xi) = \lvert \xi \rvert \hat{f}(\xi)

ということです．
逆投影フィルタを用いれば

\begin{align*}
K_{G, \Lambda G} &= \int_{-\infty}^\infty \frac{\overline{\lvert \zeta \rvert \hat{G}(\zeta)} \hat{G}(\zeta)}{\lvert \zeta \rvert} \, d\zeta\\
&= 2\pi \int_{-\infty}^\infty e^{-\zeta^2} \, d\zeta\\
&= 2\pi \sqrt{\pi}
\end{align*}

となるので(最後の等号は Gauss 積分)， $\psi(x) = (\Lambda G)(x)/(2\pi\sqrt{\pi})$ とおけば $K_{G, \psi} = 1$ となることがわかります．
これで $\psi(x)$ が求まりました！……と言いたいところなのですが， $\Lambda G$ が具体的にはどのような関数なのかがまだわかっていません．
$\Lambda G$ がどのような関数かを知るには， $\mathcal{H}G$ が求められれば十分です．
Fourier 反転公式を用いれば $\mathcal{H}G = \mathcal{F}^{-1}[(\operatorname{sgn} \xi)\hat{G}]$ を計算すればよいことがわかります．
具体的な計算は最後に回すことにして，ここでは先に答えを言ってしまうことにします．
Dawson 積分 $F(z)$ を次で定義します．⁸

F(z) = e^{-z^2} \int_0^z e^{w^2} \, dw

このとき

(\mathcal{H}G)(x) = \frac{2i}{\sqrt{\pi}} F\left(\frac{x}{\sqrt{2}}\right)

です． Dawson 積分の微分は， Leibniz 則と微分積分学の基本定理から

\begin{align*}
F'(z) &= -2z e^{-z^2} \int_0^z e^{w^2} \, dw + e^{-z^2} e^{z^2}\\
&= 1 - 2z F(z)
\end{align*}

となります．よって $\psi(x)$ は

\begin{align*}
\psi(x) &= \frac{1}{2\pi\sqrt{\pi}} (\Lambda G)(x)\\
&= \frac{1}{2\pi\sqrt{\pi}} \frac{1}{i} \frac{d}{dx} \mathcal{H}G (x)\\
&= \frac{1}{2\pi\sqrt{\pi}i} \frac{2i}{\sqrt{\pi}} F'\left(\frac{x}{\sqrt{2}}\right) \frac{1}{\sqrt{2}}\\
&= \frac{1}{\sqrt{2}\pi^2} \left(1 - 2 \frac{x}{\sqrt{2}} F\left(\frac{x}{\sqrt{2}}\right)\right)\\
&= \frac{1}{\sqrt{2}\pi^2} \left(1 - \sqrt{2}x F\left(\frac{x}{\sqrt{2}}\right)\right)
\end{align*}

と求まりました．

$\eta = G$ と組にして許容条件を満たすような関数のひとつとして $(\Lambda G) / 2\pi\sqrt{\pi}$ を見つけることができたわけですが，実は　$\psi(x) = (\Lambda G'')(x)$ とおいても $K_{\eta, \psi} \neq 0$ を満たします．
よって， $F'(x) = 1 - 2x F(x)$ を繰り返し適用し，さらに適当に定数倍すれば

\begin{align*}
\psi(x) &= \frac{1}{-\pi\sqrt{\pi}} (\Lambda G'')(x)\\
&= \frac{1}{\pi^2} \left(2x(x^2 - 3) F\left(\frac{x}{\sqrt{2}}\right) - \sqrt{2}(x^2 - 2)\right)
\end{align*}

も許容条件 $K_{\eta, \psi} = 1$ を満たすことがわかります．

数値実験

リッジレット変換・双対リッジレット変換

さて，前節までで計算した結果を使って，リッジレット変換の数値積分を計算してみましょう．
閉区間 $[-1, 1]$ 上の実数値関数 $f(x) = \sin(2\pi x)$ を学習します(区間の外側では常に $0$ をとるものとします)．
入力が $m = 1$ 次元の場合のリッジレット変換・双対リッジレット変換の式を思い出せば

\begin{align*}
T(a, b) := (\mathcal{R}_\psi f)(a, b) &= \int_{-\infty}^\infty f(x) \overline{\psi(ax - b)} \, dx\\
&= \int_{-1}^1 \sin(2\pi x) \psi(ax - b) \, dx\\
(\mathcal{R}^\dagger_\eta T)(x) &= \int_{-\infty}^\infty \int_{-\infty}^\infty T(a, b) \eta(ax - b) \, da \, db
\end{align*}

を数値積分すればよいことがわかります．
数値積分法には様々な方法がありますが，ここではわかりやすさを優先し，最も単純な区分求積法を用います．
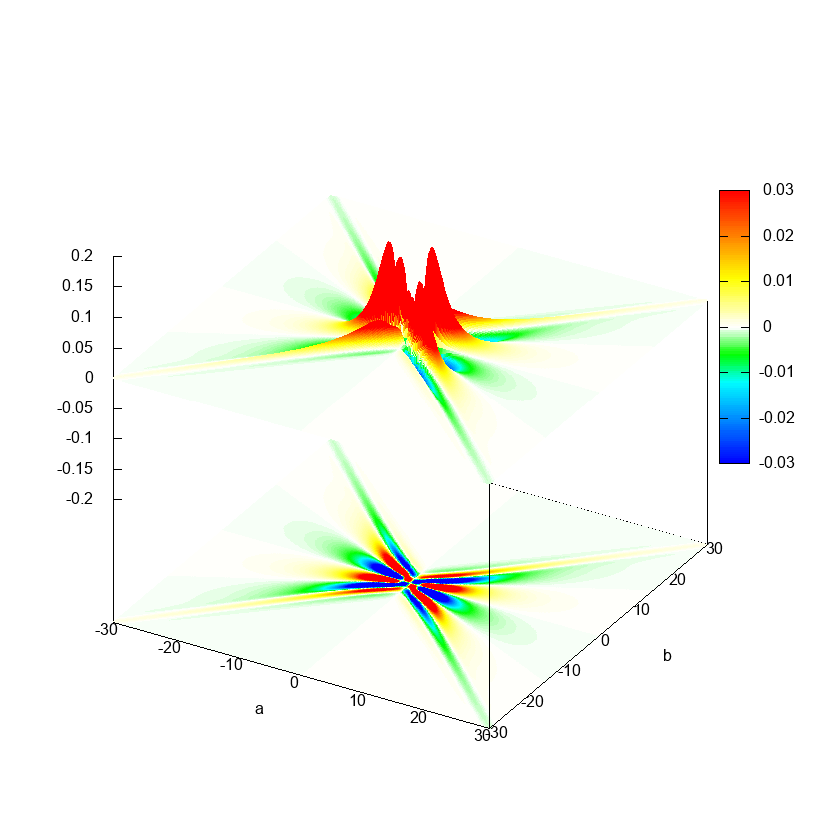
双対リッジレット変換は $(a, b) \in [-30, 30] \times [-30, 30]$ の範囲で計算することにします．
計算に使用する各種定数を $N = 200, \Delta x = 0.02, I = J = 600, \Delta a = \Delta b = 0.1$ とおき，

\begin{align*}
T(a_i, b_i) = (\mathcal{R}_\psi f)(a_i, b_j) &\approx \sum_{n = 0}^N f(x_n) \psi(a_i x_n - b_j) \Delta x\\
(\mathcal{R}^\dagger_\eta T)(x) &\approx \sum_{i = 0}^I \sum_{j = 0}^J T(a_i, b_j) \eta(a_i x_n - b_j) \Delta a \Delta b\\
&\text{where $a_i = -30 + i\Delta a, b_j = -30 + j\Delta b, x_n = -1 + n\Delta x$}
\end{align*}

を計算します．
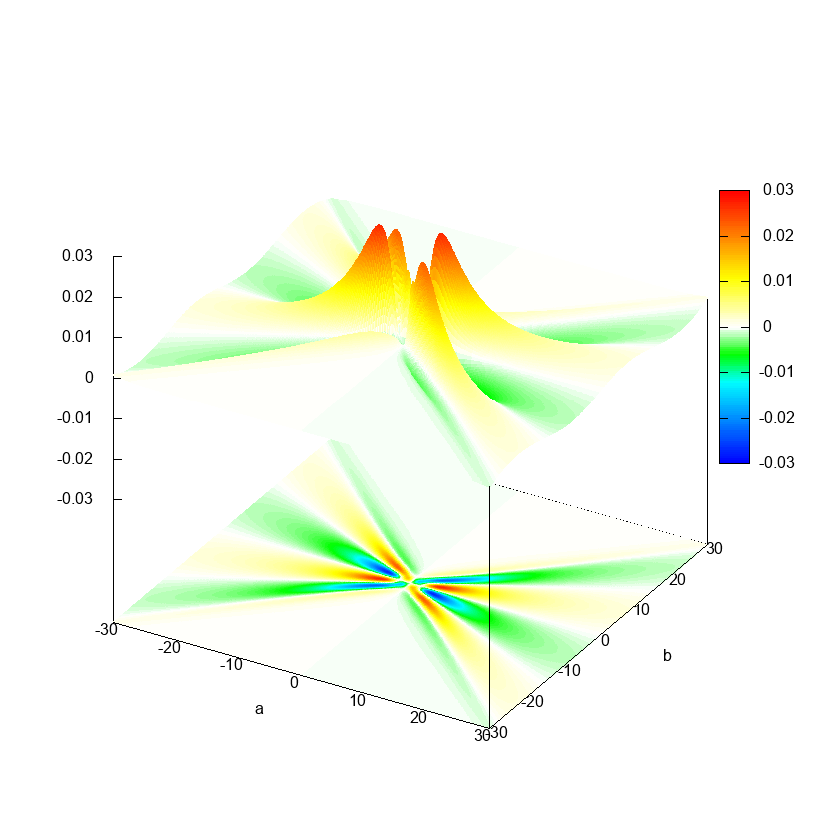
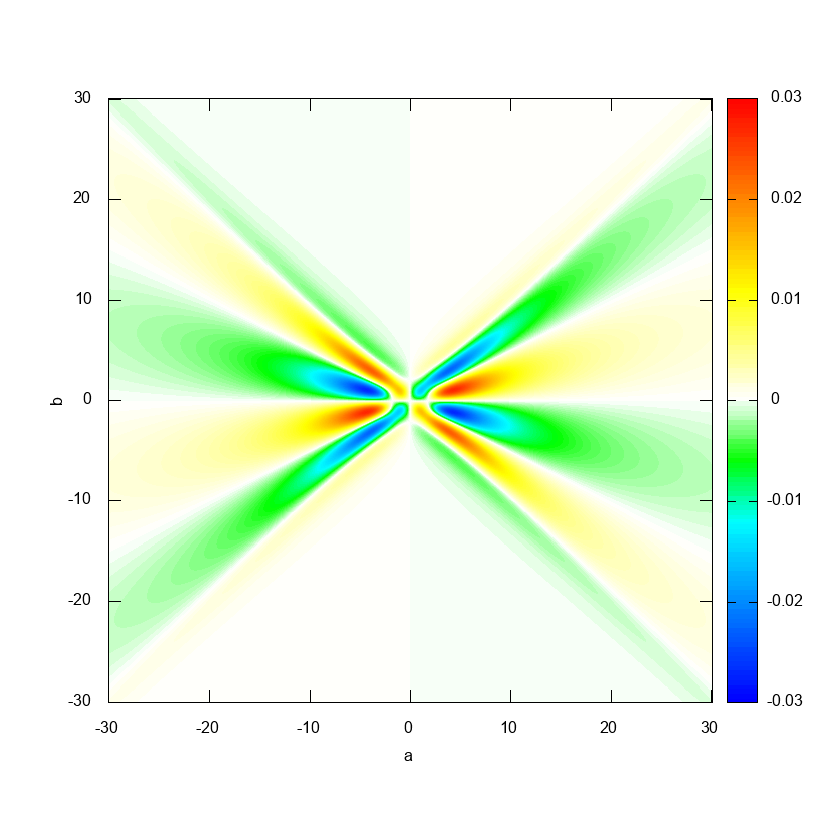
実際に Octave でリッジレット変換を計算してみた結果が以下です．

リッジレット変換の式をよく見てみると， $a$ を固定すれば $b \mapsto T(a, b)$ という関数は(おおよそ) $f(x)$ と $\psi(ax)$ の畳み込みを計算しているように思えるわけで，そういう気持ちで上の図を眺めると $a = \text{const}$ という断面がなんとなく $f(x)$ のグラフに見えるんじゃないかと思います．
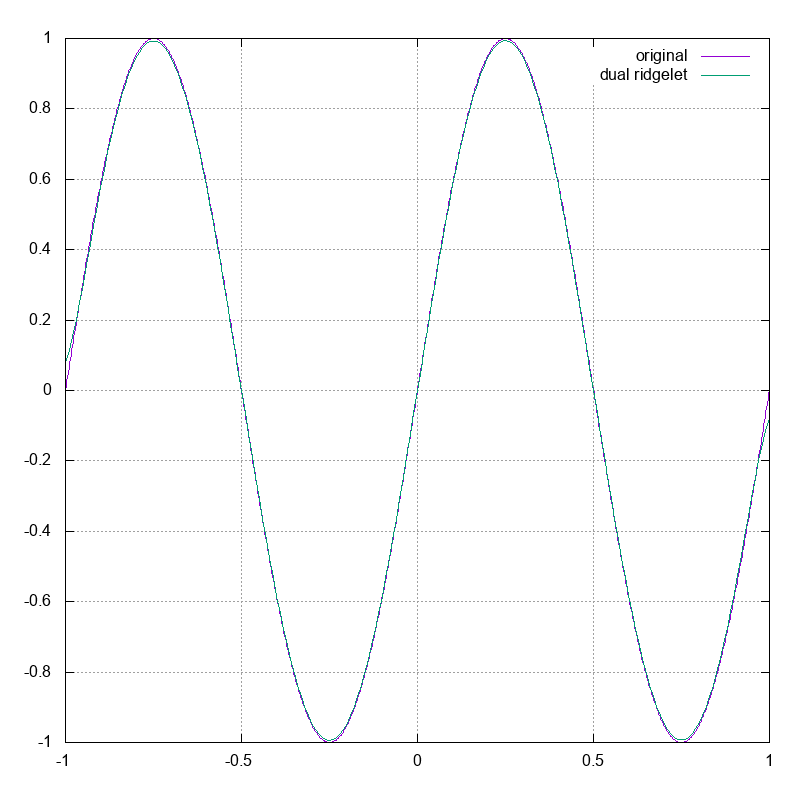
次に $\eta(x)$ による双対リッジレット変換を計算してもとの $f(x)$ が復元されることを確かめましょう．
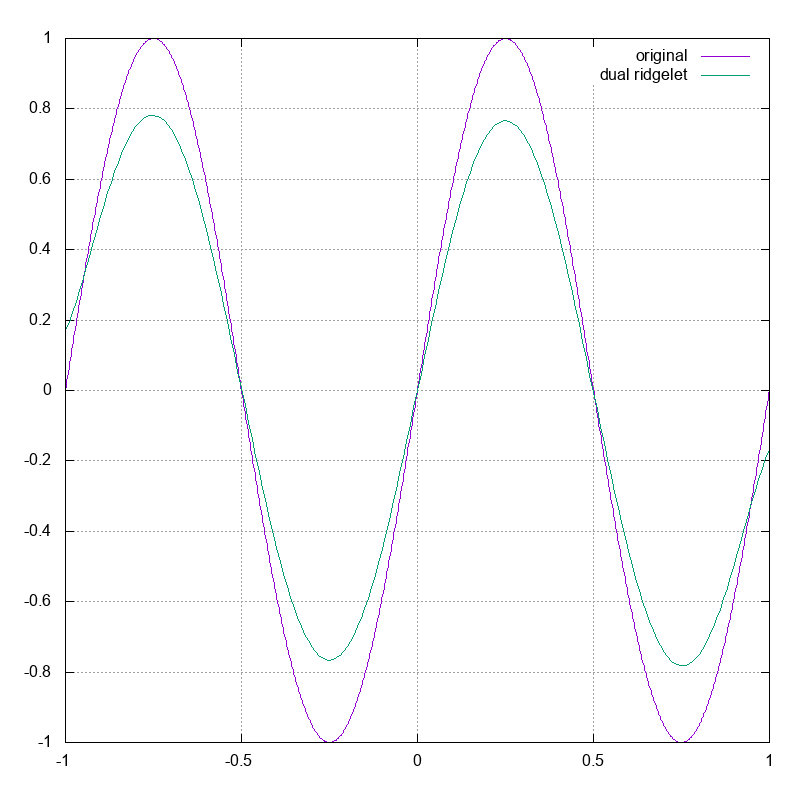
実際に Octave で双対リッジレット変換を計算してみた結果が以下です．

ちょっと定数倍ずれている気がしますが，これは二重積分の範囲を $[-30, 30] \times [-30, 30]$ に制限したことが原因と思われます．
これを確かめるために， $\psi(x) = (\Lambda G'')(x) / (-\pi\sqrt{\pi})$ の方を用いて計算してみると以下のようになります．

ぴったり復元できていますね．リッジレット変換の方のグラフを見ると，値が大きいところは中心付近に集中していて，遠方ではより急速に $0$ に近づいていることが確認できます．
このため二重積分の範囲が狭くてもより高い精度で復元できるわけです．

オラクルサンプリング

さて，ニューラルネットは双対リッジレット変換の離散化であったことを思い出しましょう．
双対リッジレット変換 $(\mathcal{R}^\dagger_\eta T)(x) = \int_{\mathbb{R} \times \mathbb{R}} T(a, b) \eta(ax - b) , da , db$ を有限和で近似したいわけですから， $T(a, b)$ の値が大きいところをニューロンの重み・バイアスとして採用すると効率良く近似できそうだと予想できます．
これを実現するために，学習したい関数 $f(x)$ の リッジレット変換 $T(a, b) = (\mathcal{R}_\psi f)(a, b)$ を重み・バイアス $(a, b)$ が従うべき確率分布とみなして ，重み・バイアスの初期値をサンプリングすることにします．
実際には以下のようにします．

1. 棄却法を用いて分布 $T(a, b)$ に従う乱数を生成し，重み・バイアスの組 $(a_j, b_j)$ を $J$ 個生成する(ここでは $J = 10$)．
2. 最小二乗法により二乗誤差 $E = \int_{-1}^1 (f(x) - \sum_{j = 1}^J c_j \eta(a_j x - b_j))^2 , dx$ が最小になるような $(c_j)_{j = 1}^J$ を求める．

$E$ を最小にするためには全ての偏微分が $0$ になればよく，計算すると

\begin{align*}
&\frac{\partial E}{\partial c_i} = \int_{-1}^1 2\left(f(x) - \sum_{j = 1}^J c_j \eta(a_j x - b_j)\right) \eta(a_i x - b_i) \, dx = 0\\
\implies& \sum_{j = 1}^J \left(\int_{-1}^1 \eta(a_i x - b_i) \eta(a_j x - b_j) \, dx\right) c_j = \int_{-1}^1 f(x)\eta(a_i x - b_i) \, dx
\end{align*}

となるので，

\mathbf{A} = \left(\int_{-1}^1 \eta(a_i x - b_i) \eta(a_j x - b_j) \, dx\right)_{i,j}, \mathbf{c} = (c_j)_j, \mathbf{b} = \left(\int_{-1}^1 f(x)\eta(a_i x - b_i) \, dx\right)_i

とおけば $\mathbf{A}\mathbf{c} = \mathbf{b}$ という連立1次方程式になるのでこれを解けばよいです(積分は実際には区分求積法で求めます)．

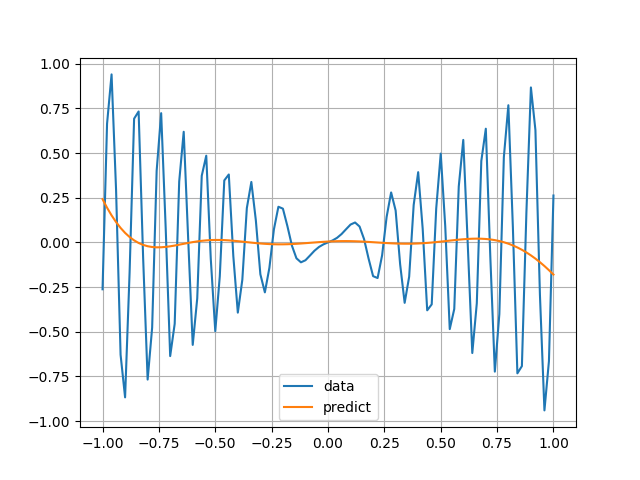
この方法で実際に重み・バイアスをサンプルしてみると例えば以下のようになります．

ランダム初期化よりマシ，という感じでしょうか． 今回の場合だと $f(x)$ が簡単すぎてよくわからないですね．

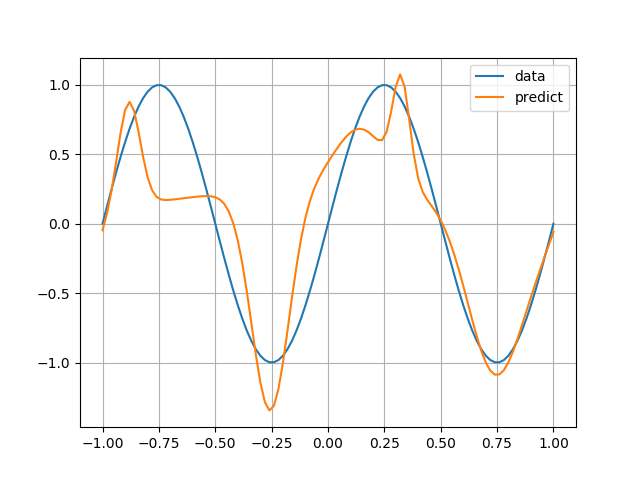
オラクルサンプリングの有効性を見るために，もう少し複雑な関数で試してみましょう．
$f(x) = -x \sin(1 / (0.1 x)^2 + 0.01)$とおきます．
隠れ層のノード数を $J = 50$ として Chainer で 1000 epoch 学習させてみると例えば以下のようになります．

全然学習できてないですね．
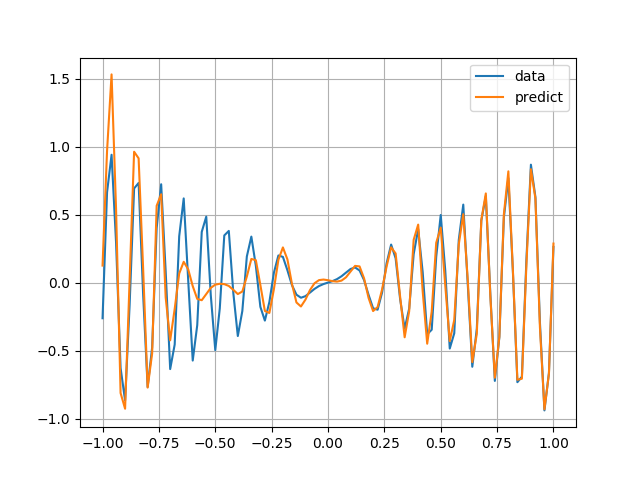
次に，オラクルサンプリングによって重み・バイアスを求めると例えば以下のようになります．

さっきよりかなりよく近似できていますね．ここから始めてトレーニングを行うとさらに精度を上げることができます．

付録: Gauss 核の Hilbert 変換が Dawson 積分を用いて書けることの証明

ここでは本文中で計算を省略した $(\mathcal{H}G)(x) = \frac{2i}{\sqrt{\pi}} F\left(\frac{x}{\sqrt{2}}\right)$ の証明をします．
Fourier反転公式を用いて計算すると，

\begin{align*}
(\mathcal{H}G)(x) &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty (\operatorname{sgn} \xi) e^{-\xi^2 / 2} e^{ix\xi} \, d\xi\\
&= \frac{1}{\sqrt{2\pi}} \left(\int_{-\infty}^0 (-e^{-\xi^2 / 2} e^{ix\xi}) \, d\xi + \int_0^\infty e^{-\xi^2 / 2} e^{ix\xi} \, d\xi\right)\\
&= \frac{1}{\sqrt{2\pi}} \left(\int_0^\infty e^{-\xi^2 / 2} (-e^{-ix\xi}) \, d\xi + \int_0^\infty e^{-\xi^2 / 2} e^{ix\xi} \, d\xi\right)\\
&= \frac{2i}{\sqrt{2\pi}} \int_0^\infty e^{-\xi^2 / 2} \sin(x\xi) \, d\xi\\
&= i\sqrt{\frac{2}{\pi}} \operatorname{Im}\left(\int_0^\infty e^{-\xi^2 / 2} e^{ix\xi} \, d\xi\right)\\
&= i\sqrt{\frac{2}{\pi}} e^{-x^2 / 2} \operatorname{Im}\left(\int_0^\infty e^{-(\xi - ix)^2 / 2} \, d\xi\right)
\end{align*}

となります．
括弧の中身の積分 $I := \int_0^\infty e^{-(\xi - ix)^2 / 2} , d\xi$ を計算するために，複素数平面上で次のような長方形の積分経路を考えます．

\begin{gather*}
C := C_1 + C_2 + C_3 + C_4,\\
\begin{aligned}
C_1 &\colon z(t) = t & (t\colon 0 \to R),\\
C_2 &\colon z(t) = R + it & (t\colon 0 \to x),\\
C_3 &\colon z(t) = t + ix & (t\colon R \to 0),\\
C_4 &\colon z(t) = it & (t\colon x \to 0).
\end{aligned}
\end{gather*}

それぞれの経路での線積分を計算すると

\begin{align*}
\int_{C_1} e^{-(z - ix)^2 / 2} \, dz &= \int_0^R e^{-(t - ix)^2 / 2} \frac{dz}{dt} \, dt\\
&= \int_0^R e^{-(t - ix)^2 / 2} \, dt,\\
\int_{C_2} e^{-(z - ix)^2 / 2} \, dz &= \int_0^x e^{-(R + it - ix)^2 / 2} \frac{dz}{dt} \, dt\\
&= i\int_0^x e^{-(R^2 + 2R(it - ix) + (it - ix)^2) / 2} \, dt\\
&= i\int_0^x e^{-(R^2 + 2R(it - ix)) / 2} e^{-(it - ix)^2 / 2} \, dt,\\
\int_{C_3} e^{-(z - ix)^2 / 2} \, dz &= \int_R^0 e^{-t^2 / 2} \frac{dz}{dt} \, dt\\
&= -\int_0^R e^{-t^2 / 2} \, dt,\\
\int_{C_4} e^{-(z - ix)^2 / 2} \, dz &= \int_x^0 e^{-(it - ix)^2 / 2} \frac{dz}{dt} \, dt\\
&= -i\int_0^x e^{-(it - ix)^2 / 2} \, dt
\end{align*}

となります．
Cauchy の積分定理から $\int_C e^{-(z - ix)^2 / 2} , dz = 0$ なので

\begin{align*}
\int_{C_1} e^{-(z - ix)^2 / 2} \, dz &= -\left(\int_{C_3} + \int_{C_2} + \int_{C_4}\right) e^{-(z - ix)^2 / 2} \, dz\\
&= \int_0^R e^{-t^2 / 2} \, dt - i\int_0^x (e^{-(R^2 + 2R(it - ix)) / 2} - 1) e^{-(it - ix)^2 / 2} \, dt
\end{align*}

となりますが，ここで両辺 $R \to \infty$ とすると， $\lvert e^{-(R^2 + 2R(it - ix)) / 2}\rvert = \lvert e^{-R^2 / 2} e^{iR(t - x)}\rvert = e^{-R^2 / 2} \to 0$ なので

\begin{align*}
I &= \sqrt{\frac{\pi}{2}} + i\int_0^x e^{-(it - ix)^2 / 2} \, dt\\
&= \sqrt{\frac{\pi}{2}} + i\int_0^x e^{(x - t)^2 / 2} \, dt
\end{align*}

となります． $w := x - t$ と置換すると

\begin{align*}
I &= \sqrt{\frac{\pi}{2}} + i\int_x^0 e^{w^2 / 2} \, (-dw)\\
&= \sqrt{\frac{\pi}{2}} + i\int_0^x e^{w^2 / 2} \, dw
\end{align*}

となります． $I$ の積分区間が $(-\infty, \infty)$ ではなく $[0, \infty)$ なので虚部が残ってしまうわけですね．
以上より

\begin{align*}
(\mathcal{H}G)(x) &= i\sqrt{\frac{2}{\pi}} e^{-x^2 / 2} \operatorname{Im}(I)\\ 
&= i\sqrt{\frac{2}{\pi}} e^{-x^2 / 2} \int_0^x e^{w^2 / 2} \, dw\\
&= \frac{2i}{\sqrt{\pi}} \cdot \frac{1}{\sqrt{2}}e^{-x^2 / 2} \int_0^x e^{w^2 / 2} \, dw\\
&= \frac{2i}{\sqrt{\pi}} e^{-(x / \sqrt{2})^2} \int_0^{x/\sqrt{2}} e^{w^2} \, dw\\
&= \frac{2i}{\sqrt{\pi}} F\left(\frac{x}{\sqrt{2}}\right)
\end{align*}

となり， $\mathcal{H}G$ を求めることができました．

参考文献

1. 園田翔・村田昇(2015)『深層学習のリッジレット解析にむけた取組み』
2. 園田翔(2015)『ニューラルネットの積分表現理論』(スライド)
3. 園田翔(2017)『深層ニューラルネットの積分表現理論』
4. S. Sonoda, N. Murata, "Neural network with unbounded activation functions is universal approximator", Appl. Comput. Harmon. Anal. 43 (2017) 233--368.
5. @konatsu (2018) 『ニューラルネットワークの積分表現理論&積分表現理論改』

1. 超関数に関しては筆者もまだよくわかってません． ↩

2. 3層パーセプトロンで表現できる関数全体の集合が $L^2(\mathbb{R}^m)$ や $C(\mathbb{R}^m)$ において稠密である，等々の意味です． ↩

3. 実は一般には $(\mathcal{R}^\dagger_\eta T)(\mathbf{x}) = \int_{\mathbb{R}^m \times \mathbb{R}} T(\mathbf{a}, b) \eta(\mathbf{a} \cdot \mathbf{x} - b) \lVert \mathbf{a} \rVert^{-s} , d\mathbf{a} , db$ なのですが，本稿では(0除算が怖いので) $s = 0$ を採用しています．
   ですから，ニューラルネット(3層パーセプトロン)は双対リッジレット変換の(離散的な)計算をしているとみなせるわけです． ↩

4. これも一般には $(\mathcal{R}_\psi f)(\mathbf{a}, b) = \int_{\mathbb{R}^m} f(\mathbf{x}) \overline{\psi(\mathbf{a} \cdot \mathbf{x} - b)} \lVert\mathbf{a}\rVert^s , d\mathbf{x}$ ( $\overline{\cdot}$ は複素共役)なのですが，ここでは $s = 0$ を採用しています． ↩

5. より一般に， $K_{\eta, \psi}$ が $0$ でない有限の値に収束すれば $(\mathcal{R}^\dagger_\eta \mathcal{R}_\psi f)(\mathbf{x}) = K_{\eta, \psi} f(\mathbf{x})$ となります． ↩

6. 工学では文字に $t, \omega$ や $t, f$ を用いることが多いですが，ここでは論文(と数学書の習慣)に倣って $x, \xi$ を用いています． ↩

7. $\operatorname{sgn} \xi$ と $i\xi$ は明らかに可換なので， 反転公式を用いれば Hilbert 変換 $\mathcal{H}$ と微分 $'$ も可換であることがわかります．つまり $\mathcal{H}(G') = (\mathcal{H}G)'$ です．
   被積分関数が実関数の方が気分が良いわけで，これをさらに $i$ で割って得られる変換 ↩

8. Octave の help dawson で表示される erfi による定義とは一見違うように見えるかもしれませんが， Maclaurin 展開して項別積分すれば $\operatorname{dawson}(z) = e^{-z^2} \sum_{n = 0}^\infty z^{2n + 1} / (n!(2n + 1)) = F(z)$ となり両者は一致することがわかります． ↩