LoginSignup
17
13
@kenjihiranabe(平鍋 健児)in株式会社永和システムマネジメント

手計算で LU 分解〜Gauss消去法の逆思考

Last updated at Posted at 2021-08-20

これは何?

  • Gilbert Strang 先生から学んだ線形代数シリーズ、第4回目の記事です。全体は以下から。

今回は、連立一次方程式を解く方法として、 $LU$ 分解を直感的に説明しようと思います。 $L$ は Lower Traiagular すなわち下三角行列、 $U$ は Upper Trainglar すなわち上三角表列です。任意の $m \times n$ 行列をこの２つの積に分解します。

計算機によって連立一次方程式 $Ax=b$ を解く場合の最もよく使われるアルゴリズムですが、大学の線形代数初学者の 手計算でもとても役に立ちます 。通常、行列 $A$ の、

  • 逆行列を求める
  • ランクを求める
  • 独立な行ベクトルを求める
  • 行列式の値を求める

などの場合に、「行基本変形」によって階段行列（正方行列の場合は上三角行列）を作る際には掃き出し法を使うことが多いと思います。すなわち、 Gaussの消去法をやると思うのですが、これは、その逆(?)思考とも呼ぶべき手法になっています。慣れると通常の行基本変形よりも分かりやすい（思考過程の係数がそのまま記録される）という利点があります。

この記事を読んだ後は、Gaussの消去法でなく、$LU$ 分解を使って手計算で上記のような問題を颯爽と解くことができるようになるでしょう！

まず結論を

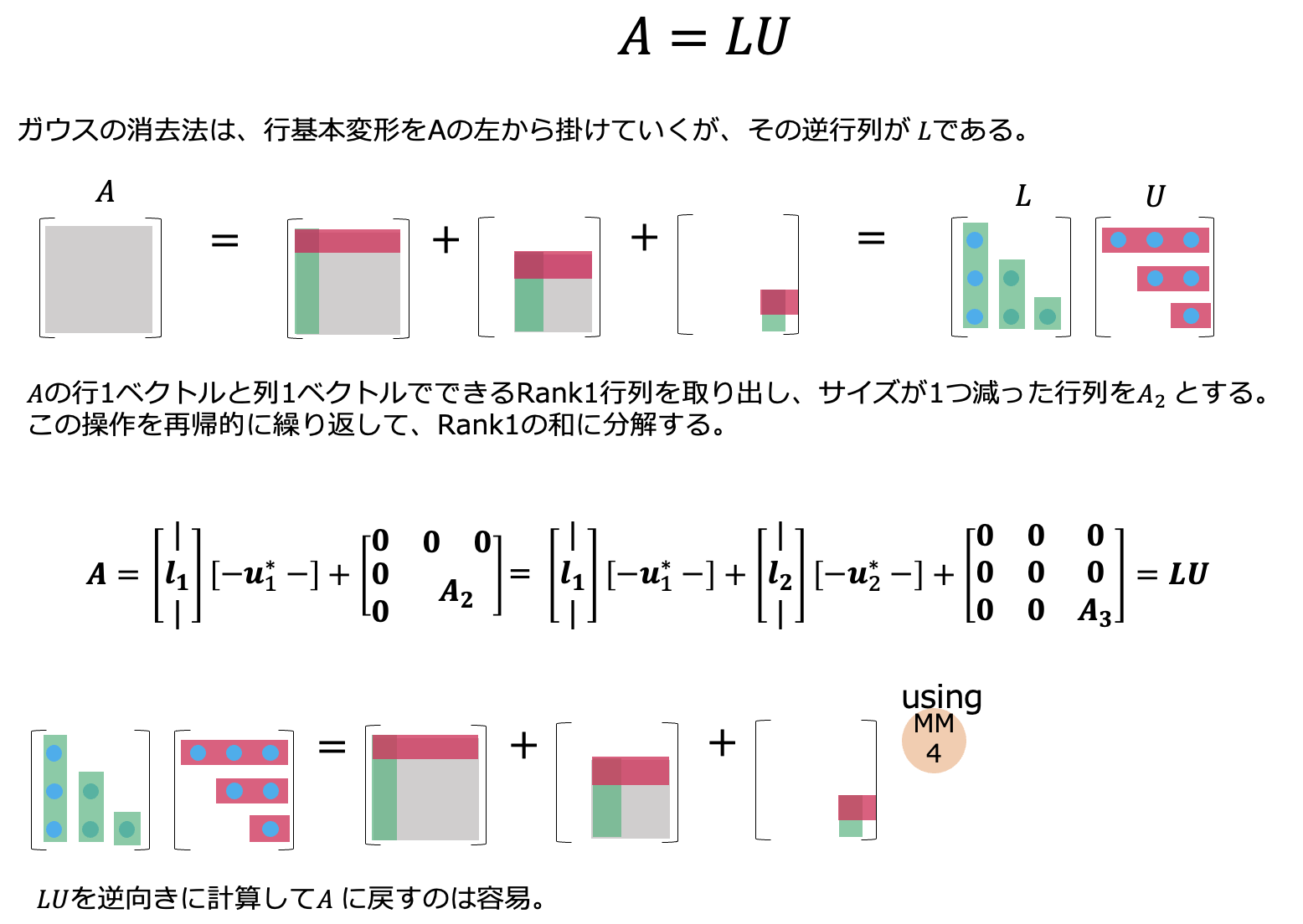
$A$ を $LU$ と分解します。これを、こんな風に解釈します。この絵がすんなり理解できる方は、以降には追加の情報がありません。
image.png
以下では、大学一年生の線形代数で学習するであろう Gauss の消去法との対比でわかりやすく解説していきます。

Gauss の消去法

見慣れた簡単な例題で、$Ax=b$を解きます。

\begin{bmatrix}
1 & 2 & 4 \\
2 & 5 & 1 \\
1 & 5 & 3 \end{bmatrix}
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix} 
= \begin{bmatrix}
9 \\ 4 \\ 7
\end{bmatrix}

通常のGaussの消去法(掃き出し法)でやってみます。1行目を使って2行目と3行目の1列目に0を作る。その後、2行目を使って3行目の2列目に0を作って、、、と言う風に、下の3角形部分を0にして行くのでした。

\begin{align}
\begin{bmatrix}A \;| \;b  \end{bmatrix} =
& \begin{bmatrix} \begin{array}{ccc|c}
1 & 2 & 4 & 9\\
2 & 5 & 1 & 4\\
1 & 5 & 3 & 7 \\
\end{array}
\end{bmatrix} \\
\begin{matrix}
\scriptsize{
\begin{array}
.②=②-2 \times ① \\
③=③-1 \times ①
\end{array}
} \\
E_1 \\
\longrightarrow 
\end{matrix}

& \begin{bmatrix} \begin{array}{ccc|c}
1 & 2 & 4 & 9\\
0 & 1 & -7 & -14\\
0 & 3 & -1 & -2 \\
\end{array}
\end{bmatrix} \\

\begin{matrix}
\scriptsize{
③=③-3 \times ②
} \\
E_2 \\
\longrightarrow
\end{matrix}

& \begin{bmatrix} \begin{array}{ccc|c}
1 & 2 & 4 & 9\\
0 & 1 & -7 & -14\\
0 & 0 & 20 & 40 \\
\end{array}
\end{bmatrix}= \begin{bmatrix} U \;| \; b'  \end{bmatrix}
\end{align}

$A$が階段行列(上三角行列） $U$ になりました。ここまでが前進消去です。できた $U$ が上三角行列になっているので、これを3行目から逆に解いて後退代入していけば、 $z=2, y=0, x=1$ の順に答えが求まります。この記事では、前進消去に注目します。

上記の消去操作は、$E_1, E_2$ で表現される行基本変形行列になっていて、これを $A$ の左に掛けていきます。ちなみにこの記事では $E$ は Elimination の略であり、 $I$ で表現される単位行列とは無関係です。それぞれ、

\begin{align}

E_1= & \begin{bmatrix} 
1 & 0 & 0 \\
\bbox[yellow]{-2} & 1 & 0 \\
\bbox[yellow]{-1} & 0 & 1 
\end{bmatrix} \qquad
E_2= & \begin{bmatrix} 
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & \bbox[yellow]{-3} & 1 
\end{bmatrix} \\

&\begin{matrix} 
 \scriptsize{
 \begin{array}
.②=② \bbox[yellow]{-2} \times ① \\
③=③ \bbox[yellow]{-1} \times ①
 \end{array}
}
\end{matrix}

&\begin{matrix} 
\scriptsize{
③=③ \bbox[yellow]{-3} \times ②
}
\end{matrix} 

\end{align}

となります。色を塗った部分が、元の行に対して他の行の定数倍を「足し込む」操作です。

各ステップで $E_1, E_2$ をこの順に左から掛け算することが、行基本変形の行列演算的な正体。左から掛けるので、並びとしては $E_2 E_1 A$ となることに注意してください。

何が起きているか

ここで行っていることは、$A$に正則な行基本行列を左から順にかけて変形し（同じように $b$ も変形し）、$A$ を上三角行行列 $U$ にしているのです。

\begin{align}
Ax &= b \\
E_1 Ax &= E_1 b \\
E_2 E_1 Ax &=  E_2 E_1 b
\end{align}

累積した $E_1, E_2$ をまとめて $E=E_2 E_1$ として、さらに、結果としてできる上三角行列を $U$ とすると、

\begin{align}
E A x &= E b \\
Ux &= b'
\end{align}

となります。ここまでが前進消去です。

EA  = U \tag 1

となっていることを覚えておいてください。これは、$A$ に $E=E_2 E_1$ という行基本変形行列を左から掛けたら $U$ になる、ということです。

各ステップで左から掛け算することが、行基本変形の行列演算的な正体。色を塗った部分が、元の行に対して他の行の定数倍を「足し込む」操作になるのです。最終的には行列の掛け算によって、 $E$ 全体が求まります。

LUを使ってAを分解する

さて、本題です。

EA = U \tag 1

と変形したのですから、

A = E^{-1}U

です。$E$ が行基本変形行列で正則ですから、 $E^{-1}$ が必ず存在します。この $E^{-1}$ を $L$ として下三角行列で表現したものが、$LU$ 分解、

A = LU

です。この記事では、$E$ ではなく、直接 $L=E^{-1}$を直接計算してやろう、というのです。どちらの手法でも、$U$ は求まります。なお、 $LU$ 分解も、Gaussの消去法同様、 $A$ が正則でない場合や、長方行列の場合でも可能です。Gaussの消去法を使う場面として、連立方程式の解法や逆行列以外にも、ランクや解の有無についての情報を炙り出したことを思い出してください。どちらの方法も、$A$が非正則や長方行列の場合でも実行可能であり、 $E, L$ は正則行列、$U$ は $A$ と同じサイズの階段行列となります。

LU で分解する

同じ問題で、$A$ を $LU$分解します。まず、1行目に着目し、これを使って２行目の1列目と3行目の1列目を0に持っていきます。変形が → でなく、= で繋がっていることに注目してください。 $A$ から1列目の2,3行目を0にして $U_1$ へと変形すると考え、$L$ の要素を埋めていきます。

\begin{align}
A =
& \begin{bmatrix}
1 & 2 & 4 \\
2 & 5 & 1 \\
1 & 5 & 3 \\
\end{bmatrix} \\

A = L_1 U_1 =
& \begin{bmatrix}
1 & 0 & 0 \\
\bbox[yellow]{2} & 1 & 0 \\
\bbox[yellow]{1} & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 4 \\
0 & 1 & -7 \\
0 & 3 & -1 \\
\end{bmatrix}
\quad
\begin{matrix}
\scriptsize{
 \begin{array}
.U_1②=A② - \bbox[yellow]{2} \times A① \\
U_1③=A③ - \bbox[yellow]{1} \times A①
 \end{array}
}
\end{matrix}
\end{align}

まずここまでです。 $A$の一行目（これを $A①$ と書きます)を維持し、そのまま右側の $U_1$ の1行目とします。そして、$L_1$ の1行目に、$[1, 0, 0]$ を埋めます。これで、$A$ の1行目が計算できます。$A①=U_1①$ です。$A$の1行目は必ず $[1, 0, 0]$ であり、$U_1$ の１行目は必ずオリジナルの $A$ の1行目です。

次に、$A$ の1行目を使って２行目に0を作るために、$A① \times 2$ を $A②$ から引き去ります。この引き算する倍数(=2)を $L_1$ の $(2,1)$ 要素に書くのです。そして、引いた結果を $U_1$ の2行目に残します。同様に、 $A① \times 1$ をA③ から引き去ります。この引き算する倍数(=1)を $L_1$ の $(3,1)$ 要素に書きます。そして、引いた結果を $U_1$ の3行目に残します。

これで、1列目が消去できました。大丈夫でしたか？ 目で追えればOKです。再度、右側を計算して、 $A=L_1 U_1$ となっていることを行ごとに確かめてください。

  • $A①=U_1① $
  • $A②=U_1②+2 \times U① $
  • $A③=U_1③+1 \times A① $

となることが分かりますか？ 目の動きとしてはこんな感じです。
image.png
さて、次に 2行目を使って3行目に0を作ります。ここで $U_1$ を見て引き去る数を決めます。2行目の3倍を3行目から引きます。

\begin{align}
A =
& \begin{bmatrix}
1 & 2 & 4 \\
2 & 5 & 1 \\
1 & 5 & 3 \\
\end{bmatrix} \\
A=L_1 U_1 =
& \begin{bmatrix}
1 & 0 & 0 \\
\bbox[yellow]{2} & 1 & 0 \\
\bbox[yellow]{1} & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 4 \\
0 & 1 & -7 \\
0 & 3 & -1 \\
\end{bmatrix} \quad
\begin{matrix} 
\scriptsize{
 \begin{array}
.U_1②=A② - \bbox[yellow]{2} \times A① \\
U_1③=A③ - \bbox[yellow]{1} \times A①
 \end{array}
}
\end{matrix} \\
A = L U =
& \begin{bmatrix}
1 & 0 & 0 \\
\bbox[yellow]{2} & 1 & 0 \\
\bbox[yellow]{1} & \bbox[yellow]{3} & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 4 \\
0 & 1 & -7 \\
0 & 0 & 20 \\
\end{bmatrix}
\quad
\begin{matrix}
\scriptsize{
\begin{array}
.U②=A② - \bbox[yellow]{2} \times A① \\
U③=A③ - \bbox[yellow]{1} \times A①　 \\
U③=U_1③ - \bbox[yellow]{3} \times U_1②
 \end{array}
}
\end{matrix}

\end{align}

これで、 $LU$ 分解の出来上がりです。$LU$　それぞれの行列が下上三角行列になっていること、さらに、 $L$ の対角行列が 1 になっていることに注目してください。そして、最後に検算してみてください。

  • $A①=U① $
  • $A②=2 \times U① + U②$
  • $A③=U① + 3 \times U② + U③$

image.png

ここでは、$L$ にこれまでのプロセスが累積的に記述されています($L_1, L_2$ などとそれぞれの記録を残しません)。その累積は、$A$ の各行から「引き去る」係数が $L$ の書く黄色く塗った要素にはっきりと見えます。実は $E$ を使うとこうは行かないのです。

EとLの大きな違い

$E$ の計算では $A$ の各行に「足し込む係数」が行列に表現され、黄色でハイライトしたように -1, -2, -3 が $E_1, E_2$ のそれぞれの要素に出てきました。逆に、 $L$ のそれぞれの要素には、1,2,3 が $A$ の各行から「引き去る係数」が $L$ に出てきます。これはなんとなく、当然な気がします。$L = E^{-1}$なので。

でも、一番の効果は累積したときの係数です。 上の例では、$L$ をそのまま累積的に記述しています。$E = E_2 E_1$ を実際に計算してみると、

\begin{align}
E_2 E_1
& = \begin{bmatrix} 
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & \bbox[yellow]{-3} & 1 
\end{bmatrix}
\begin{bmatrix} 
1 & 0 & 0 \\
\bbox[yellow]{-2} & 1 & 0 \\
\bbox[yellow]{-1} & 0 & 1 
\end{bmatrix} \\

&= \begin{bmatrix} 
1 & 0 & 0 \\
\bbox[yellow]{-2} & 1 & 0 \\
\bbox[yellow]{(-2)(-3)-1} & 0 & 1 
\end{bmatrix} = E

\end{align}

となって、掃き出しに使った係数が混ざってしまうのです。 $L$ だとそんなことはありません。素直に書く係数が要素に出てきます。

L =
\begin{bmatrix}
1 & 0 & 0 \\
\bbox[yellow]{2} & 1 & 0 \\
\bbox[yellow]{1} & \bbox[yellow]{3} & 1 \\
\end{bmatrix}

他にも、 $A=LU$ と分解する利点は、一旦この分解を保持しておけば、$Ax=b$ の $b$ が変わってもすぐに解けるということ、それに、計算機的には$LU$両方をいっぺんに保持するのに元の$A$と同じ大きさのメモリしか必要としない、ということもあります(対角の1は記憶する必要がありません)。巨大な行列を扱う場合に、 $A$ の領域を使って$L, U$の両方を格納して $A$ を上書きしてしまい、メモリを節約することができます($LU$ から $A$ は簡単に復元できます)。

Aをrank1行列の「和」に分解する

もう１つ、 $LU$ 分解の面白い解釈を紹介したいと思います。一見、 $A=LU$ と行列の「積」に分解しているように見えますが、これを行列の和に分解している、と見ることもできるのです。個々の行列は rank1 行列と言われる行列です。

準備: rank1 行列

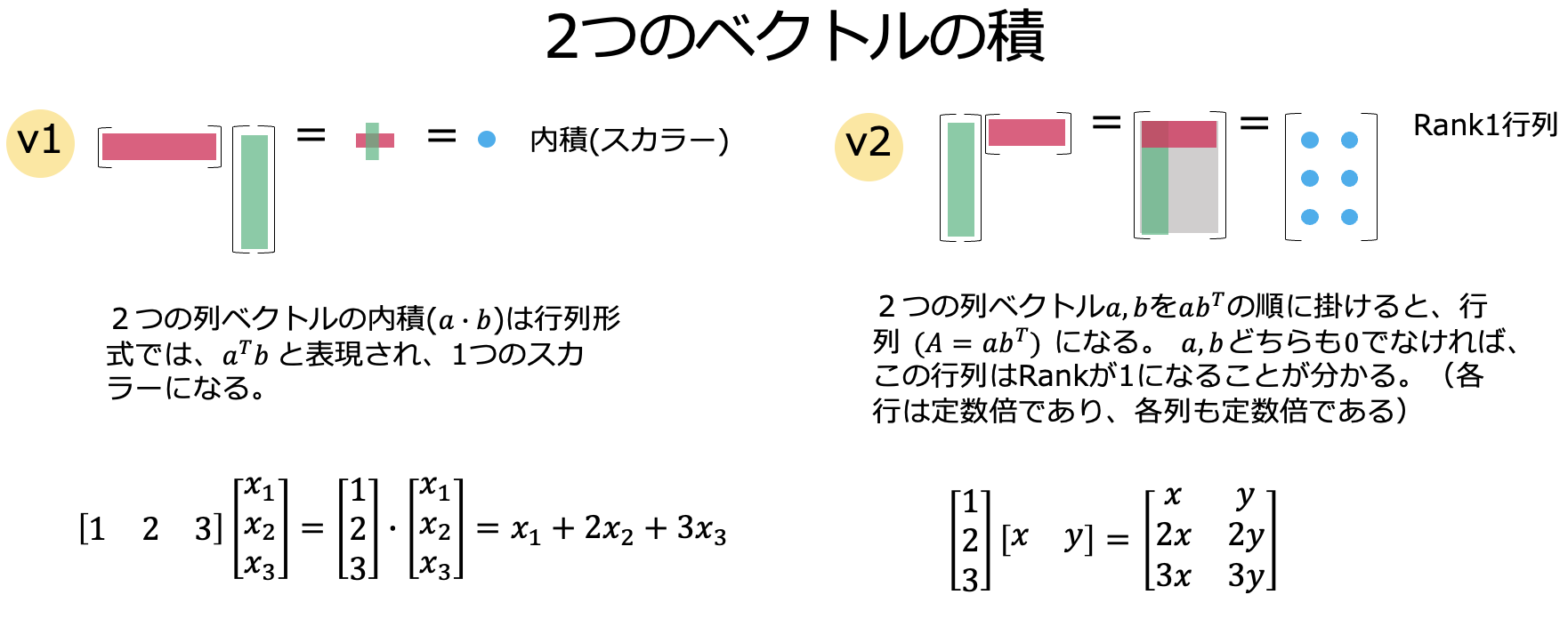
一つだけ軽い準備です。rank1行列というものを定義しましょう。 $a, b$ を$0$でない列ベクトルとします。転置を右肩の$T$で表現すると、$a^T$は行ベクトルになります。

まず、 $a, b$ が同一サイズの場合に、

a^Tb = c \tag{v1}

が計算できます。この「行ベクトル×列ベクトル」は数（スカラー）になります。これは「内積」ですね。では、

ab^T = C \tag{v1}

「列ベクトル×行ベクトル」はどうなるでしょう。この場合は $a, b$ のサイズが違ってもよく、 $a$ を $n \times 1$ 、 $b$ を $m \times 1$ とすると $C$ には、 $n \times m$ の行列ができます。この行列をrank1行列と言います。

この行列のランクが1になることが分かりますか？ 各行が定数倍の関係になること、同様に、各列が定数倍になることを確認してください。すなわち、この行列のランクは1です（ただし、$a, b$ どちらかのベクトルが $0$ であればランクは0です）。

こんなイメージで覚えるとよいでしょう。

image.png
図： 内積とrank1行列

Aの皮をLUで剥いでいく

もう一度、$LU$ 分解の第一段階を見てみましょう。

\begin{align}
A =
& \begin{bmatrix}
1 & 2 & 4 \\
2 & 5 & 1 \\
1 & 5 & 3 \\
\end{bmatrix} \\

A = L_1 U_1 =
& \begin{bmatrix}
1 & 0 & 0 \\
\bbox[yellow]{2} & 1 & 0 \\
\bbox[yellow]{1} & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 4 \\
0 & 1 & -7 \\
0 & 3 & -1 \\
\end{bmatrix}
\quad
\begin{matrix}
\scriptsize{
\begin{array}
.U_1②=A② - \bbox[yellow]{2} \times A① \\
U_1③=A③ - \bbox[yellow]{1} \times A①
\end{array}
}
\end{matrix}
\end{align}

これをみると、$L1$ の1列目と $U1$ の1行目でできる rank1行列を $A$ から抜き出している、と読めます。1行目の定数倍を2,3行目から引いて、残りが右下の $2 \times 2$行列に現れます($A_2$)。

A = L_1 U_1 =
\begin{bmatrix}
1 \\ 2 \\ 1
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 4
\end{bmatrix}　+ 
\begin{bmatrix}
0 & 0 & 0 \\
0 & 1 & -7 \\
0 & 3 & -1 \\
\end{bmatrix}

この右下の $A_2$ をさらに同じように皮を剥いでいきます。

A_2 = \begin{bmatrix}
1 & -7 \\
3 & -1
\end{bmatrix} = 
\begin{bmatrix}
1 \\ 3
\end{bmatrix}
\begin{bmatrix}
1 & -7
\end{bmatrix}　+ 
\begin{bmatrix}
0 & 0 \\
0 & 20 \\
\end{bmatrix}

$L$ 行と $U$ の列の掛け算では、どちらの第1要素を1にするか自由度が残りますが、必ず $U$ には前の行をそのままに、 $L$ の対角要素が1になるようにします。

最後に右下に $20$ が残りました。もとの $LU$ と比べてみましょう。

\begin{align}
A = L U =
&\begin{bmatrix}
1 & 0 & 0 \\
\bbox[yellow]{2} & 1 & 0 \\
\bbox[yellow]{1} & \bbox[yellow]{3} & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 4 \\
0 & 1 & -7 \\
0 & 0 & 20
\end{bmatrix}　\\
= &\begin{bmatrix}
1 \\ 2 \\ 1
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 4
\end{bmatrix}
+ \begin{bmatrix}
0 \\ 1 \\ 3
\end{bmatrix}
\begin{bmatrix}
0 & 1 & -7
\end{bmatrix}
+ \begin{bmatrix}
0 \\ 0 \\ 1
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 20
\end{bmatrix}
\end{align}

$A$ の1行目と1列目が共通するrank1行列をそれらの掛け算として作り、それを元の $A$ から取り出します。すると、$A$ の1行目と1列目がすべて0になったものが残ります。残りの1次元小さくなった行列 $A_2$ で、これを再帰的に繰り返して、右下に1つの数が残るまで続けるのです。順次引いていった rank1行列を足し算すると、もとの $A$ が復元されます。

可視化すると、こんな感じです。
image.png

最後に美しい式を書いておきます。
最初は和分解で、各項がrank1行列です。次が積分解です。

A = \sum_{k=1}^{n} \begin{bmatrix}l_i u_i\end{bmatrix} = 
\begin{bmatrix}
l_1 l_2 \cdots l_n
\end{bmatrix}
\begin{bmatrix}
u_1 \\ u_2 \\ \vdots \\ u_n
\end{bmatrix} = LU

書き残したこと

プロセスを複雑にしたくなかったので、1つだけズルをしたことがあります。それは、$A$ のピボットに0が現れる場合です。その場合、行の交換の必要が起こります。行の交換も、正則な行基本変形ですから、その交換行列を $P$ とすると、正確には、

PA = LU

となります。が、まぁ、理論的な理解の大勢には影響ないでしょう。

問題

ここまでの内容が理解できたかどうか、最後に問題を出しておきます。

問

(1)　次の行列 $A$ を$LU$分解し、掛け算の形($LU$) と足し算の形($\sum l_i u_i$)に分解しなさい。 ("Linear Algebra for Everyone" より)

A = \begin{bmatrix}
a & a & a & a \\
a & b & b & b \\
a & b & c & c \\
a & b & c & d
\end{bmatrix}

(2) 次の行列 $A$ を$LU$分解し、ランク（階数）を求めなさい。(長方行列であることに注意。この場合 $U$ は $A$ と同じサイズであり、$L$ は正方で正則となるように分解する。)

A = \begin{bmatrix}
1 & 1 & 1 & 2 \\
2 & 2 & 3 & 4 \\
3 & 3 & 8 & 11
\end{bmatrix}

行列の掛け算を可視化

Gilbert先生は $A$ の分解を「目の慣れ」を重視して講義を進めています。こんな可視化に興味がある方は、こちらにまとまった資料

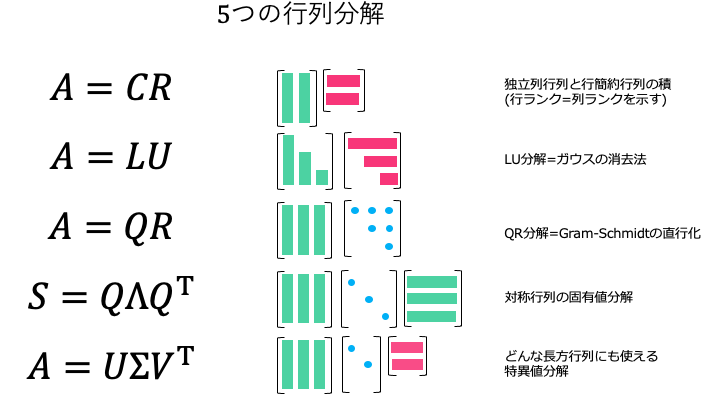
があります。私はこれを推し進めて、先生の提唱する行列5分解を、今後解説していこうと思います。今回が、この3回目、$LU$ 分解だったというわけです。初回は、$CR$ 分解を使って、「行列の行ランクと列ランクはなぜ等しいか」というテーマを扱っていますので、ぜひそちらもご覧ください。

5つの行列分解全部については、こんな感じです。

image.png

参考文献

  • Gilbert 先生の他の線形代数やデータサイエンスの書籍について。(こちらの別記事)

本が出ました

このシリーズについて

このシリーズでは、Gilbert Strang 先生の Linear Algebra Vision 2020 を元に、この後、$CR$分解だけでなく、$LU$分解, $QR$分解(Gram-Schmidt), 固有値分解, 特異値分解(SVD) を扱っていきます。

Gilbert Strang 先生は MIT の有名な（名物）線形代数の先生です。OpenCourseware で無償で先生の講義をみることができます。

という日本語の著書があります。

今後、シリーズ化して先生の講義から目から鱗の話題を解説する予定です。

先生については、別のページで紹介します(日本語版は別途用意中)。

17
13
3

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
17
13