はじめに
「友達の友達は友達だ!」 というノリの人がいます。もし、全人類がこのノリだったらどうなるでしょう。
「友達の友達は友達」の処理をグラフ理論で考えると、あるネットワーク(グラフ)において、距離2以内(友達または友達の友達)のノード同士をすべて直接つなぎ直す操作に対応します。
この操作を何度も繰り返すと、最終的には(元が連結グラフの場合)、すべてのノードが隣接(直接つながる)する完全グラフになるはずです。つまり、「世界中全員が友達」 になるということです。
そこでこの記事では、「友達の友達は友達」の処理を何回繰り返すと「世界中全員が友達」になるのか、考えていきます。
以下の流れで進めていきます。
- 問題設定と前提
- グラフ理論的な視点
- 「友達の友達は友達」操作を繰り返すと何が起きるか
- 六次の隔たり(Six Degrees of Separation)との関係
- まとめと考察
ネタ記事です。数学的にそんなに厳密じゃないかも。
1. 問題設定と前提
まずは前提となる設定を確認します。
-
元のネットワーク(グラフ)を $G_1 = (V, E_1)$ とする
- 頂点集合 $V$ は「世界中の人々」を表すとする。頂点数は有限(人類の人数)である。
- 辺集合 $E_1$ は「直接の友達関係」を表し、無向グラフとする。
-
「友達の友達は友達」の処理を1度行ったグラフを $G_2 = (V, E_2)$ と定義する
- $G_2$ では、もともと $G_1$ で距離(最短経路長)が2以下だったすべてのノード間に辺を張り足す。
- 結果として、$G_2$ は「$G_1$ 上で距離が1または2の頂点同士が直接つながるグラフ」になる。
- 同様に、「友達の友達は友達」の処理を$(n-1)$回行ったグラフを $G_n = (V, E_n)$ と定義する
本記事で考えるべきことは以下のように書き替えることができます。
元グラフ $G_1$(人間のつながり網)に対し、「距離2以内を隣接にする」操作を $k$ 回行った $G_{k+1}$ が完全グラフとなるような$k$を求める。
また、本記事では以下を仮定することとします。
- 「世界中の人々」の元グラフが連結(分離されていない)である
- 頂点間の最大距離(直径)が6である(六次の隔たり)
2. グラフ理論的な視点
操作を繰り返すたびに、「元グラフ $G_1$ 上での距離がどこまで隣接になるか」を確認します。
2.1 距離の定義
- ここで、$d_G(u,v)$ はグラフ $G$ における頂点 $u$ と $v$ の最短距離(経路長)を表します。
- たとえば、$d_{G_1}(u,v) = 1$ ならば $u$ と $v$ は $G_1$ 上で直接隣接(友達)であり、
- $d_{G_1}(u,v) = 2$ ならば「友達の友達」の関係にあたります。
2.2 「友達の友達は友達」の処理と距離
-
$G_1$
- 操作前の元グラフなので、$d_{G_1}(u,v) = 1$ のノード(直接の友達)だけが隣接する。
-
1回目の操作:$G_1 \to G_2$
- 定義より、$G_2$ では「$G_1$ 上で距離 $\le 2$ の頂点同士をすべて隣接にする」。
- すなわち、任意の $u,v \in V$ について
$$
d_{G_1}(u,v) \le 2 \quad\Longrightarrow\quad (u,v)\in E_2.
$$
-
2回目の操作:$G_2 \to G_3$
- $G_3$ では「$G_2$ 上で距離 $\le 2$ の頂点同士をすべて隣接にする」。
- このとき、$d_{G_3}(u,v)$ が元 $G_1$ の距離 $d_{G_1}(u,v)$ とどのような関係になるか?
-
一般に $n$ 回目の操作:$G_n \to G_{n+1}$
- $G_{n+1}$ では「$G_n$ 上で距離 $\le 2$ の頂点同士をすべて隣接にする」。
- このとき、$d_{G_{n+1}}(u,v)$ が元 $G_1$ の距離 $d_{G_1}(u,v)$ とどのような関係になるか?
次に、「「友達の友達は友達」の処理によって距離がどれだけ圧縮されるか」を見ていきます。
2.3 距離圧縮のイメージ
「友達の友達は友達」による距離圧縮
$G_{n+1}$ において、任意の頂点 $u,v$ の距離は、
$$
d_{G_{n+1}}(u,v) \le \left\lceil \frac{d_{G_n}(u,v)}{2} \right\rceil
$$
のように振る舞う。(※ $\lceil \cdot \rceil$ は天井関数(切り上げ)を意味する。)
- 理由の概要
-
$d_{G_n}(u,v) \le 2$ ならば、$u,v$ は $G_{n+1}$ 上で直接隣接するため、$d_{G_{n+1}}(u,v)=1$ となる。
-
$d_{G_n}(u,v) = 3$ の場合、たとえば $u \to w \to x \to v$ のような距離3の経路があると、$G_{n+1}$ 上では「$u \to x$(元の距離2を1とみなす)$\to v$」という2ステップの経路が存在し、$\lceil 3/2 \rceil = 2$ となる。
-
一般に $d_{G_n}(u,v) = k$ のときも、2つ飛ばしでつなぐイメージを繰り返せば、最終的に $\lceil k/2 \rceil$ になると直感的に捉えられる。
これを前提として、「友達の友達は友達」の処理を繰り返したとき、「元の $G_1$ 上で距離がどのくらい圧縮されるか」を考える。
3. 「友達の友達は友達」操作を繰り返すと何が起きるか
前章で見た距離圧縮の性質を踏まえ、本章では実際に回数ごとにどこまで隣接が広がるかを確認します。
3.1 1回目の操作結果
-
操作前($G_1$)
- 元の友達関係だけがある。$d_{G_1}(u,v) = 1$ のノード同士が隣接。
-
操作後($G_2$)
-
「元の $G_1$ 上で距離 $\le 2$ のノードすべてが直接つながる」ため、
$$
d_{G_1}(u,v) \le 2 \quad\Longrightarrow\quad (u,v)\in E_2
$$ -
結果、$G_2$ 上の距離は概ね以下のように圧縮されるとイメージできる:
$$
d_{G_2}(u,v) \le \left\lceil \frac{d_{G_1}(u,v)}{2} \right\rceil
$$
-
つまり、元のグラフで距離が1や2だったノード同士はすべて距離1(直接の隣接)となります。
3.2 2回目の操作結果
-
操作前($G_2$)
- 1回目の操作によって、元 $G_1$ 上で距離2以内のペアはすでに $G_2$ 上で隣接になっている。
- たとえば元 $G_1$ 上で距離3のペアは、$G_2$ 上で距離2に圧縮されていると考えられる。
-
操作後($G_3$)
-
「$G_2$ 上で距離 $\le 2$ のノードすべてに辺を張る」ため、
$$
d_{G_2}(u,v) \le 2 \quad\Longrightarrow\quad (u,v)\in E_3
$$ -
ここで、$d_{G_2}(u,v) = \left\lceil \frac{d_{G_1}(u,v)}{2} \right\rceil$ とみなすと、
$$
d_{G_2}(u,v)\le 2
\iff \left\lceil \frac{d_{G_1}(u,v)}{2} \right\rceil \le 2
\iff d_{G_1}(u,v)\le 4
$$ -
したがって、元の $G_1$ 上で距離が「4 以下」のノードペアはすべて $G_3$ で隣接になります。
-
まとめると、2回目の操作後の $G_3$ では、
元の $G_1$ 上で距離 $\le 4$ のノード同士がすべて直接つながっている
という状態になります。
3.3 3回目の操作結果
-
操作前($G_3$)
- 2回の操作によって、元の $G_1$ 上で距離 $\le 4$ のペアはすでに $G_3$ 上で隣接になっている。
-
操作後($G_4$)
-
「$G_3$ 上で距離 $\le 2$ のノードペアすべてを隣接にする」ため、
$$
d_{G_3}(u,v)\le 2 \quad\Longrightarrow\quad (u,v)\in E_4
$$ -
同様に「$G_3$ 上の距離は元 $G_1$ 上の距離を4で割って丸めたもの」とみなすと、
$$
d_{G_3}(u,v) = \left\lceil \frac{d_{G_1}(u,v)}{4} \right\rceil
\quad\Longrightarrow\quad
d_{G_3}(u,v)\le 2
\iff \left\lceil \frac{d_{G_1}(u,v)}{4} \right\rceil \le 2
\iff d_{G_1}(u,v)\le 8
$$ -
よって、元の $G_1$ 上で距離が「8 以下」のノードペアはすべて $G_4$ で隣接になります。
-
まとめると、3回目の操作後の $G_4$ では、
元の $G_1$ 上で距離 $\le 8$ のノード同士がすべて直接つながっている
という状態になります。
イメージ(BAモデル(N=30,新規エッジ=2)に実行。Python,networkxで作成)
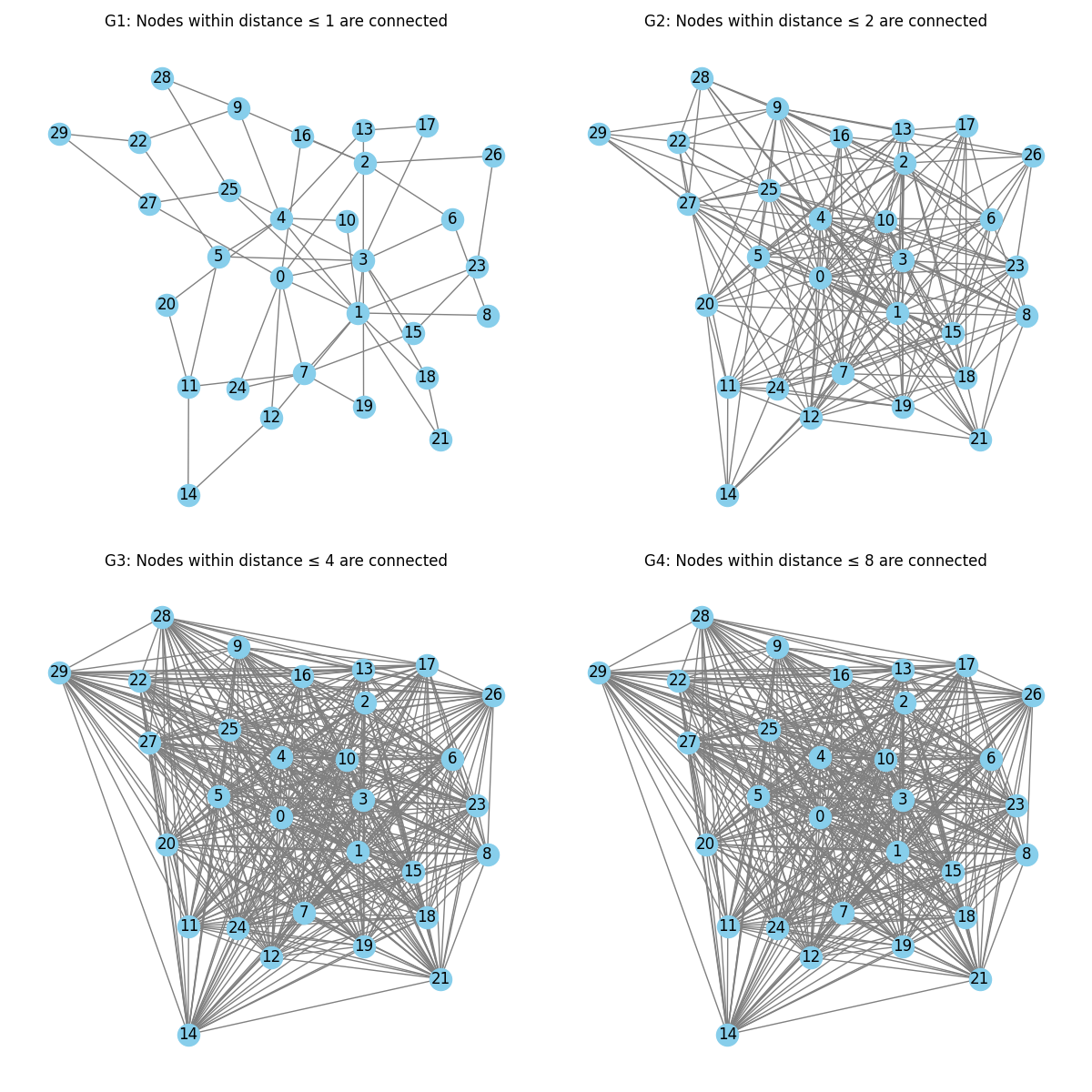
4. 六次の隔たりとの関係
ここまでで「3回の操作を行うと、元の $G_1$ 上で距離 $\le 8$ のすべてのノードペアが隣接になる」という性質が分かりました。
いったん話しはかわりまして、 六次の隔たり(Six Degrees of Separation) というネットワークにおける経験則をご存じでしょうか。
4.1 六次の隔たりとは
-
六次の隔たり
「世界中のどんな2人も、6人ほどを介せば直接のつながりがある(距離6 以下)」という経験則です。
この経験則はソーシャルネットワーク分析や実際の調査(Milgram の実験など)から導かれています。もちろん地域やコミュニティによってばらつきはありますが、概ね「6」という数字がよく取り上げられます。
4.2 「3回操作で距離8までが隣接」→「完全グラフ」の結び付き
- 元の $G_1$ において、任意の2人 $u,v$ は最大でも距離6(あるいはそれ以下)でつながると仮定する。
- 3回の「友達の友達は友達」操作を経て得られる $G_4$ は、「元の $G_1$ 上で距離 $\le 8$ のペアすべてを隣接としたグラフ」になる。
- したがって、元の距離が6以下である全ペアは当然「距離 $\le 8$」でもあるため、すべてのペアが $G_4$ 上で直接つながることになる。
- つまり、$G_4$ は完全グラフであり、あらゆる2人は「友達」に相当する隣接関係を持つ。
- その結果、「3回処理を行ったら完全グラフになる」 ことが言えます。
5. まとめと考察
この記事では、「友達の友達は友達」という操作をグラフ理論的に形式化し、3回繰り返すことで最終的に完全グラフを得る仕組みを示しました。ポイントは以下のとおりです。
-
操作の繰り返しによる距離の圧縮
- $G_2$ では元の $G_1$ 上で距離 $\le 2$ のペアがすべて隣接となる。
- $G_3$ では元の $G_1$ 上で距離 $\le 4$ のペアがすべて隣接となる。
- $G_4$ では元の $G_1$ 上で距離 $\le 8$ のペアがすべて隣接となる。
-
六次の隔たりを用いると
- 元のネットワークが連結かつ直径(最大距離)が6と仮定すれば、3回操作して得られる $G_4$ は、元の距離が「6 以下であるすべてのペア」を含め「距離 $\le 8$ のすべてのペア」を隣接とする。
- 結果的に、$G_4$ は完全グラフとなる。
したがって、「友達の友達は友達」の処理を3回施すと「世界中全員が友達」になる ということになります。
おわりに
本記事では、グラフ理論的な視点と六次の隔たりの経験則を組み合わせ、「友達の友達は友達」の処理を何回繰り返すと「世界中全員が友達」になるのか という問いを明らかにしました。3回という結論になりましたが、直観よりもかなり小さい値だと思います(「友達の友達は友達だ!」 というノリを全員に仮定しているので、かなり強い仮定をしてはいますが...)。
とはいえ、ちょっとの勇気で交流関係は一気に広がるのかもしれません。Let’s connect!