[1707.05300] Reverse Curriculum Generation for Reinforcement Learning
メタ情報
- CoRL 2017 (1st Conference on Robot Learning)
- UC Berkeley + Oxford Robot Institute + OpenAI (←Pieter Abbeel!)
-
Reverse curriculum generation for Reinforcement Learning
- ↑動画あり
概要
- ゴール志向 (goal-oriented) タスクは報酬が疎で、学習信号を受け取るには膨大な試行をする必要がある
- 例えば鍵を錠に差し込んで回すなど
- これまでは、エキスパートのデモンストレーションを利用する方法や報酬設計をする方法が用いられてきた
- この研究では事前知識を使わない方法を提案する
- ただし、「どの状態がゴールなのか」は既知
- エージェントはゴールから「逆順に」少しずつ学習を進める
- この研究では事前知識を使わない方法を提案する
導入
- 発想:
- ゴールに近い状態からなら、ゴールするのは簡単
- ゴールに近い状態からなら、ランダム行動を取ってもまた別の有望な状態へ行ける
- アプローチ:
- ゴールに近い開始状態からゴールまでを学習させる
- 開始状態をゴールから少し遠ざける
- この逆順からタスクを解くアプローチは動的計画法にインスパイアされている
- エージェントは自分でカリキュラムを設計するようになっている
関連研究
(略)
問題設定
- 頑健性を確保するため、開始状態の集合 $S^0$ はできるだけ大きく、終了状態の集合 $S^g$ はできるだけ小さくする
reverse curriculum generation の仮定
- エピソード開始時点で、任意の状態へのリセットが可能である
- 終了状態が少なくとも1つ以上ある
- ランダム行動を取った時のマルコフ連鎖が既約 (連結類) になっている 1
仮定1と2の組み合わせにより、「エピソード開始時点で、終了状態の近くの状態にリセット」が可能になる。
仮定3から、終了状態から開始して任意の開始状態に進むことが可能になる。
手法
修正開始状態での方策最適化
- 開始状態を生成する分布は与えられた開始状態集合の一様分布とする: $\rho = \text{Unif}(S^0)$
- ただし $S^0 = \{ s_0 \mid R_{\min} < R(\pi, s_0) < R_{\max} \}$ 、つまり「今の方策 $\pi$ でのタスクの期待報酬 $R(\pi, s_0)$ (=成功確率とみなせる) がハイパーパラメータ $R_{\min}$ 以上 $R_{\max}$ 以下になる」ようにする
- エージェントがゴールに いつもではないが そこそこ辿り着くという意味で、これを「良い開始状態 2」と呼ぶ
- ただし $S^0 = \{ s_0 \mid R_{\min} < R(\pi, s_0) < R_{\max} \}$ 、つまり「今の方策 $\pi$ でのタスクの期待報酬 $R(\pi, s_0)$ (=成功確率とみなせる) がハイパーパラメータ $R_{\min}$ 以上 $R_{\max}$ 以下になる」ようにする
実現可能な「近い」状態のサンプリング
- ロボットの制御タスクでは、小さなノイズを状態に付与するというのは現実的ではない
- 各ジョイントに対しては非常に小さな摂動でも、最終的なアームの位置は大きくズレて実行不可能になるかもしれない
- よって状態の「近さ」はユークリッド距離ではなく、MDP における到達可能性で測る
- つまり行動空間でのノイズ (=ブラウン運動のような) によって「近い」状態を得る
アルゴリズム詳細

- Algorithm1
- Iter の回数は5回
-
train_polは具体的には TRPO- ただし、on-policy であれば何でも良い
- 前の Iter の開始状態も $starts_{old}$ として再利用する
-
train_polの中で実際に報酬が観測されているはずなので、その値を使って「良い開始状態」かどうかを判定して残す
-
- 提案法は、ゴールに到達できる状態空間を (徐々に) 拡張している
- 重点的に学習すべきサンプルを増やし、現在の方策で報酬がまず貰えないサンプルを避ける
実験結果
MuJoCo で実験 (詳細は付録 A.1 を見よ)

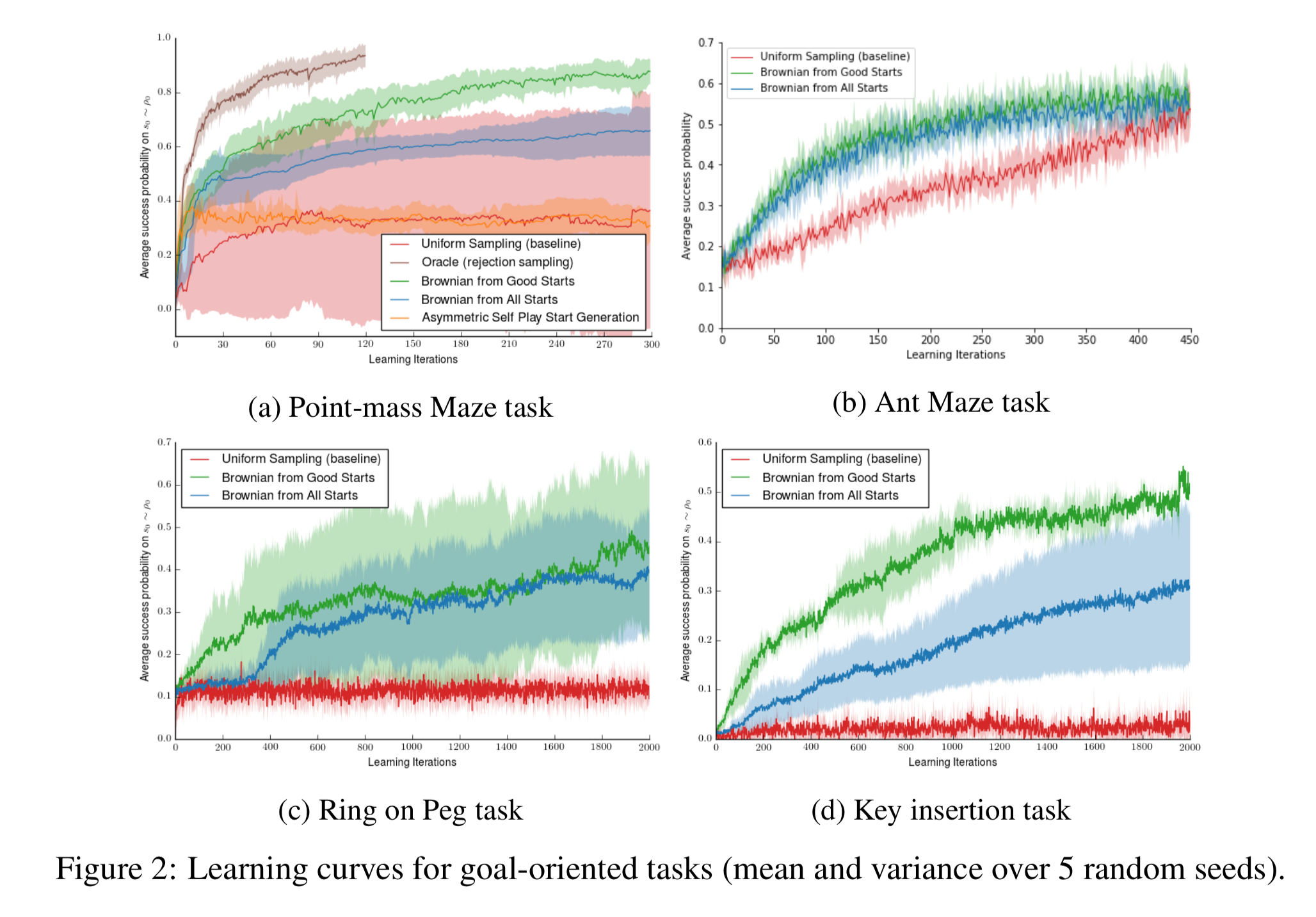
用意した実験タスクは全部で4つ:
a. Point-mass maze task: 単なる点としてのエージェントでGの字型の迷路
b. Ant maze task: 4足ロボットエージェントでUの字型の迷路
c. Ring on Peg task: 7自由度ロボットで四角いディスクを棒に指す
d. Key insertion task: 7自由度ロボットで鍵を錠に入れて回す
開始状態に分布を入れた効果

赤が開始状態分布を修正しないベースライン、青と緑が提案法。
(c) と (d) については、ベースラインの成功率が 10% と 2% になっているが、これは開始状態が偶然ゴールに近かったときである。実際には学習できていない
「良い状態」の効果
青線は、緑線から、「良い状態」かどうかの判定を取り去ったもの (=その開始状態から始めて実際に得られた報酬による「良い状態」判定をおこなわずに過去の開始状態すべてを用いるもの)。
緑のほうが青より良い。
(a) の図の茶色の線 (oracle) は、「良い状態」の判定に、実際に得られた報酬一度きりではなく、もっとたくさん回して期待値を近似したものを使った場合。(時間がかかるので (a) でしかやっていない)
確かに「良い状態」の効果があることがわかる。(提案法でも多少のロスはあるものの、その恩恵は受けている。計算効率は圧倒的に良い)
ブラウン運動による「近い」状態の生成
使ったほうが良いよ
結論と将来の方向性
- 事前知識があるなら、開始状態の分布に好みの構造を入れるのも面白い
- 提案法は開始状態の生成だが、これまでよく研究されている「ゴール生成」カリキュラムと組み合わせるのも面白い
- 実世界への応用についても課題
参考資料
- 論文と紹介ページ (動画あり)
- Reverse Curriculum Generation for Reinforcement Learning · Issue #525 · arXivTimes/arXivTimes
感想
- ゴール志向タスクを解くには、sub-goal を適切に設定するというアプローチがよく研究されている気がするが、この論文では goal 側ではなく start 側をいじるというアプローチになっている
- 確かに学習はそちらのほうが易しそうだが、sub-goal のアプローチのほうでは解釈しやすさとか合理性みたいなものが得られるのも長所な気がする
- 仮定3が少し強めな気がする。ゴールから逆順に辿れる問題は意外と少ないのではないだろうか?
- Atari だって逆再生はできないので、仮定3は成り立っていない
-
既約 (rreducible)、連結類 (communicating class)。どの状態からでも任意の状態にいける確率がゼロではない。https://ja.wikipedia.org/wiki/%E3%83%9E%E3%83%AB%E3%82%B3%E3%83%95%E9%80%A3%E9%8E%96#%E5%8F%AF%E7%B4%84%E6%80%A7 ↩
-
good starts ↩