セグメント木について【競技プログラミング】

はじめに

• LIS(Longest Increase Subsequence)というアルゴリズムを使ってとある問題を解こうと思ったんだけど、単純に作ると$O(N^2)$の計算量となって、TLEになったんだよね。
• 高速化手法を使うとO(N･logN)となって、その高速化手法が2つ有る（ニブタン、セグ木）あるからニブタンで解こうと思ったら、その問題は単純なLISでなく応用的な問題だったから、ニブタンでは対応できずセグ木一択だったよ。
• と言うわけで、セグ木に取り組むこととなったよ。でも以前、似ているフェニック木の投稿をしたから、イメージは出来ている。

フェニック木との比較

• フェニック木では、下図の番号から1を引いた数と配列のインデックスを紐付けてデータを格納する。
  

• フェニック木の計算量

  処理	オリジナル配列	累積和配列	フェニック木
  値更新	O(1)	O(N)	O(logN)
  累積和計算	O(N)	O(1)	O(logN)

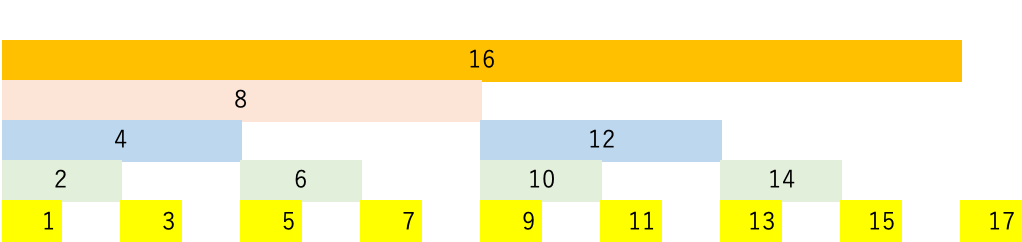
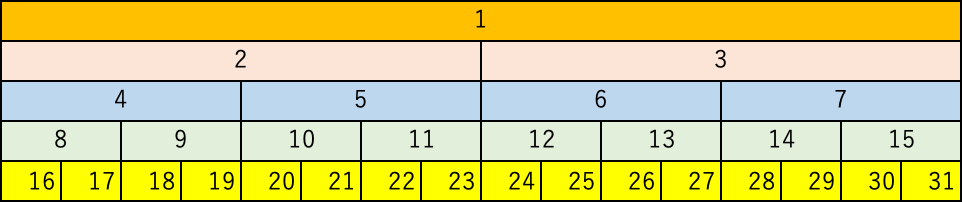
• セグ木では、下図の番号を配列のインデックスを紐付けてデータを格納するのが一般的(つまり、インデックス0の要素は使われない)。また、オリジナルの操作対象の配列の値は、最下層の葉の部分(16〜31のマス)に格納する。
  

• セグ木の各種作業の計算量も概ね木の高さに依存するので、O(logN)となります。ただし、最初の構築時はO(N)となります。

• セグ木で出来ることは？と生成AIに聞いたところ、以下の回答があった。

  • 範囲合計クエリ (Range Sum Query)
    • 指定した範囲内の要素の合計を求めます。例えば、配列のインデックス1から4までの要素の合計を計算する場合などです。
  • 範囲最小値クエリ (Range Minimum Query)
    • 指定した範囲内の要素の最小値を求めます。これは、区間の最小値を効率的に見つけるのに便利です。
  • 範囲最大値クエリ (Range Maximum Query)
    • 指定した範囲内の要素の最大値を求めます。これは、区間の最大値を効率的に見つけるのに役立ちます。
  • 範囲の積クエリ (Range Product Query)
    • 指定した範囲内の要素の積を求めることもできます。ただし、オーバーフローに注意が必要です。
  • 範囲GCDクエリ (Range GCD Query)
    • 指定した範囲内の要素の最大公約数を求めます。特定の問題で役立つことがあります。
  • 範囲更新クエリ (Range Update Query)
    • 特定の範囲内のすべての要素を一度に更新する操作です。例えば、全ての要素をある値に変更する場合などです。
  • 範囲逆数クエリ (Range Reciprocal Sum Query)
    • 指定した範囲内の要素の逆数の和を求めるクエリです。逆数の和を計算する必要がある特定の問題で使えます。

• うむ、何か見えてきた！これって、一つのセグ木で全て対応できるわけではなく、やりたいクエリ毎にセグ木を作らないといけない感じかな？

• 図示したセグ木の番号で言えば、1から15のマスでは、対応する16〜31のマスのクエリの結果を入れておくと言うことだね。例えば、「範囲最小値クエリ」をやりたいとき、マス5には、マス20〜23の最小値が入っている、ということ。「範囲更新クエリ」以外は、そう考えれば、イメージがつくね。

• 毛色の違う「範囲更新クエリ」は、更新を1要素毎でなく、範囲全体で行うときに、1要素毎に行うより効率的におこなうクエリとのこと。セグメント木と遅延伝播（lazy propagation）を組み合わせることで、効率的に範囲更新を行えます、だってさ。範囲更新クエリについては、今回はパスかな。･･･翌月、頑張ってやっつけました。

区間積クエリのためのセグ木の例

• 生成AIにコードを作って貰った。

class SegmentTree {
    // private var tree: [Int] -- 解説用にtreeの中身を見たいので、privateを削った。
    var tree: [Int]
    private var n: Int
    private var mod: Int

    init(_ nums: [Int], mod: Int = 1_000_000_007) {
        self.n = nums.count
        self.mod = mod
        self.tree = Array(repeating: 1, count: 2 * n)
        buildTree(nums)
    }

    private func buildTree(_ nums: [Int]) {
        for i in 0..<n {
            tree[i + n] = nums[i] % mod
        }
        for i in stride(from: n - 1, through: 1, by: -1) {
            tree[i] = (tree[i * 2] * tree[i * 2 + 1]) % mod
        }
    }

    func update(index: Int, value: Int) {
        var i = index + n
        tree[i] = value % mod
        while i > 1 {
            i /= 2
            tree[i] = (tree[i * 2] * tree[i * 2 + 1]) % mod
        }
    }

    func query(left: Int, right: Int) -> Int {
        var l = left + n
        var r = right + n
        var product = 1
        while l < r {
            if l % 2 == 1 {
                product = (product * tree[l]) % mod
                l += 1
            }
            if r % 2 == 1 {
                r -= 1
                product = (product * tree[r]) % mod
            }
            l /= 2
            r /= 2
        }
        return product
    }
}

• 生成AIの作った利用例。

let nums = [1, 2, 3, 4, 5, 6]
let segTree = SegmentTree(nums)
print(segTree.query(left: 1, right: 4)) // 出力: 24 (2 * 3 * 4)
segTree.update(index: 2, value: 10)
print(segTree.query(left: 1, right: 4)) // 出力: 80 (2 * 10 * 4)

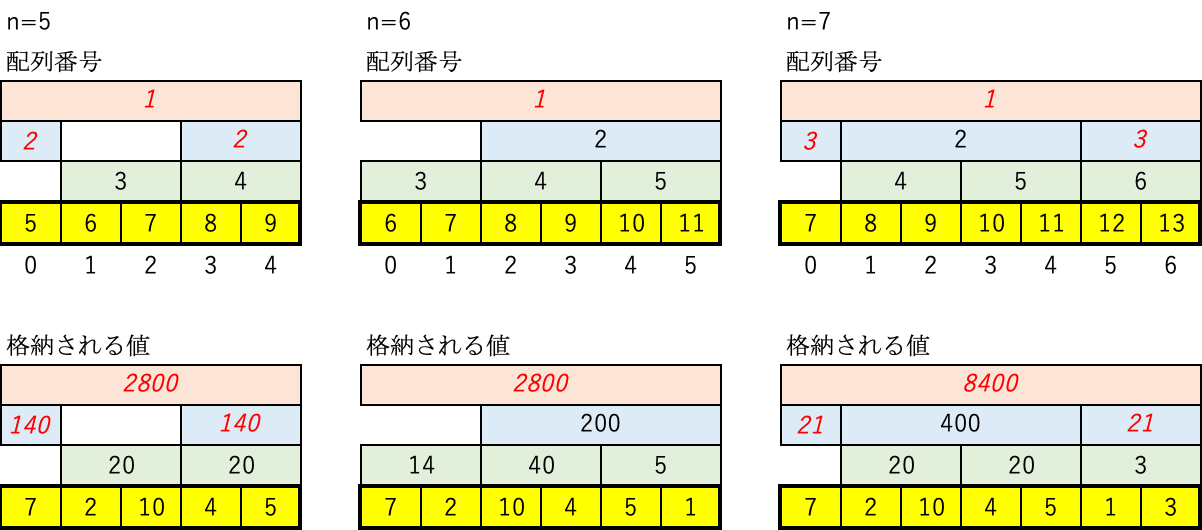
• 分析対象の配列と、セグ木配列の関係性を頭に入れやすいように、利用例を作ってみた。分析対象の配列のサイズn=5,6,7の例です。また、この利用例によって生成されるセグ木の配列番号と、セグ木に格納される値を図にしています。

let nums = [7, 2, 10, 4, 5, 1, 3]
let segTree5 = SegmentTree(Array(nums[0..<5]))
let segTree6 = SegmentTree(Array(nums[0..<6]))
let segTree7 = SegmentTree(nums)

print(segTree5.tree) // [1, 2800, 140, 20, 20, 7, 2, 10, 4, 5]
print(segTree6.tree) // [1, 2800, 200, 14, 40, 5, 7, 2, 10, 4, 5, 1]
print(segTree7.tree) // [1, 8400, 400, 21, 20, 20, 3, 7, 2, 10, 4, 5, 1, 3]

• まず、コード中のbuildTree関数で行っていることを確認します。なお、コード例は(mod 1000000007)で計算されていますが、以降の説明では完全無視します。
  • 最初のforループで、分析対象の配列numsの中身を、セグ木の葉の部分[n..<2n]に格納しています。
  • 次のforループで、葉の親部分[1..<n]の値を更新していきます。
    • 親の配列番号=子の配列番号/2。つまり、セグ木の各マスの番号を2で割った値が上のマスの番号になります。
    • このセグ木は範囲積クエリのためのモノなので、各マスは､下のマス同士を乗じた値になってます。
  • 図中の赤い数値は、せっかく作ったセグ木だけど、目的である範囲積を計算するときに使われない部分です。
    • 例えば、分析対象数列numsの全てを乗じるときに計算に使われるセグ木の配列は...
      • n=5のとき「5,3,4」で、結果は7×20×20=2800。
      • n=6のとき「3,2」で、結果が14×200＝2800。
      • n=7のとき「7,2,6」で、結果は7×400×3=8400。
      • 詳しいことは、次の行以降で説明します。
• 次に、範囲積クエリを実行するquery(l,r)関数を分析します。
  • l,rを引数にしますが、コレは、numsの部分配列[l..<r]の範囲積を計算することを意味します。
  • numsのインデックスをセグ木のインデックスにするため、nを加えます。
  • productは求める範囲積を格納する変数です。初期値を1としています。
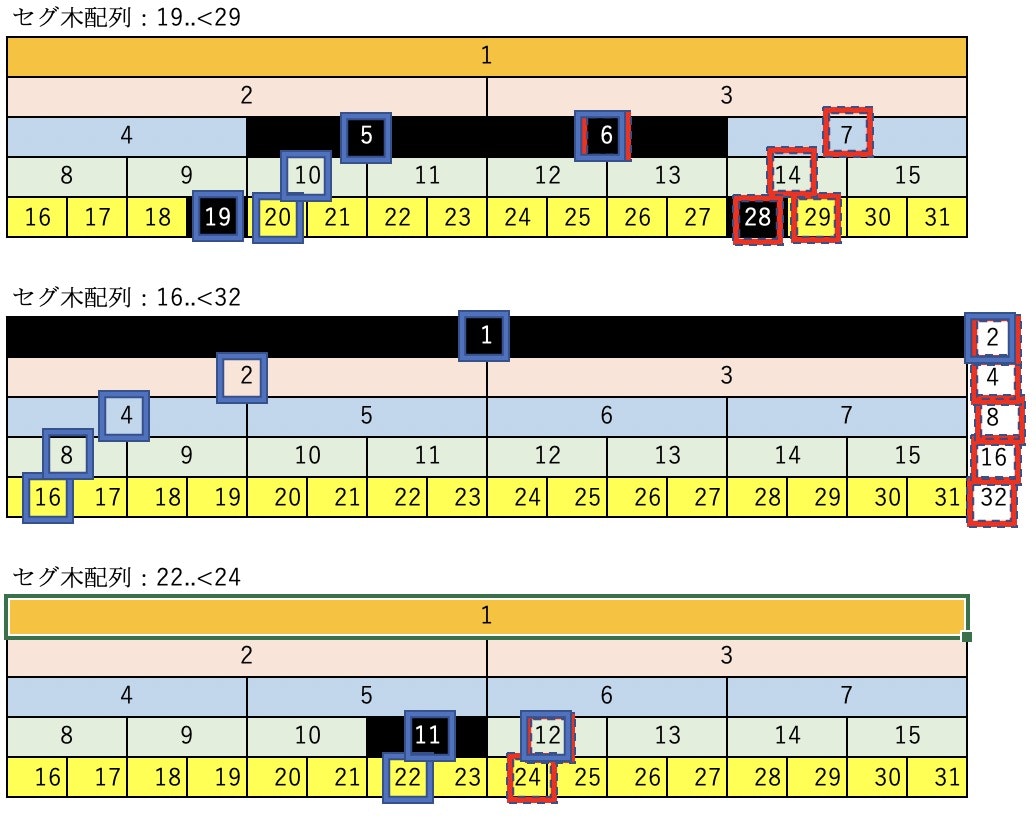
  • whileループにより、セグ木の下部（葉の方）から計算を行っていきます。
  • 下図は、青枠がlの推移、赤枠がrの推移、白抜きマスは範囲積計算に使うマスを指します。
    • 例えば、セグ木配列:19..<29の範囲積は、マス「19,5,6,28」の各値を乗じたものになります。
      • 青枠は、偶数の時は上に上がります。奇数の時は、そのマスを計算に使います。そして、右に1ズレてから上に移動します。
      • 赤枠は、偶数の時は上に上がります。奇数の時は、左にずれてからそのマスを計算に使います。そして上に移動します。
      • 青枠と赤枠が重なったら終了です。
        
• 最後に、値更新を行うupdate(i,v)を説明します。
  • nums[i]の値をvに更新します。
  • セグ木のインデックスにするため、iにnを加えます。
  • whileループ毎にi /= 2を行い、セグ木の上に向かってtree[i]を塗り替えていきます。
  • tree[0]は使わないので、i=1となったらループを止めます。
• 以上！

おわりに

• セグ木は、フェニック木をやった後なら大して難しくないね。
• でも、エクセルを使って、図示するのが面倒だったよ。まぁ、将来の自分の為にも分かり易くしておくのは重要だから、しょうがないね。
• フェニック木も、たった2か月前でも殆ど忘れてたからね。自分の投稿を見て思い出せたよ。
• とにかく、これで、LISの話にもどれます。LISの投稿を終えたら、ここにリンク貼るね。
  【後日追記】投稿したので貼っておきます。

おまけ

• 範囲最大値クエリ版も載せておきます。
• 汎用性を持たせるため、プロパティの「base=-Int.max」と「biOpe=max」を変更すれば他のクエリも可能になるようにしてます。
  • 例えば、範囲積クエリ用なら、base=1、biOpe={$0*$1 % 1000000007}にします。
• そう言えば、数学的なことを何も書いてなかったけど、セグ木は、モノイドの概念を知っておいた方が良いよ。
  • biOpeは結合律を満たす必要があり、baseは単位元となるモノを設定しないといけない。
    
  • 学生時代なら、結合律を満たす二項演算として、加算と乗算だけを思い浮かべただろうけど、今なら、max関数が結合律を見たし、この時、負の無限大（-Int.maxで代用）が単位元になる事が分かるよね。

class SegTree {
    private var tree: [Int]
    private var n: Int
    private var base: Int = -Int.max // 範囲積クエリの時はクエリの時は1にする
    private var biOpe:(_ l:Int,_ r:Int)->Int = max // 範囲積クエリの時は{$0 * $1 % 1000000007}にする
    var top :Int {tree[1]} // treeの最上位を返す

    init(_ nums: [Int]){
        self.n = nums.count
        self.tree = Array(repeating: 0, count: 2 * n)
        buildTree(nums)
    }
    convenience init(_ n:Int,v: Int = 0){
        let nums = [Int](repeating:v,count:n)
        self.init(nums)
    }


    // func biOpe(_ l:Int,_ r:Int)->Int{ 
    //     return max(l,r) // クラスプロパティで代入することにしました。
    // }
    func biOpe(_ i:Int)->Int{ // 引数1つのときの関数オーバーロード
        return biOpe(tree[2*i],tree[2*i+1])
    }

    private func buildTree(_ nums: [Int]) {
        for i in 0..<n {
            tree[i + n] = nums[i]
        }
        for i in stride(from: n - 1, through: 1, by: -1) {
            tree[i] = biOpe(i)
        }
    }

    func update(_ index: Int, _ value: Int) {
        var i = index + n
        tree[i] = value
        while i > 1 {
            i /= 2
            tree[i] = biOpe(i)
        }
    }

    func query(_ left: Int, _ right: Int) -> Int {
        var l = left + n
        var r = right + n
        var ans = base
        while l < r {
            if l % 2 == 1 {
                ans = biOpe(ans,tree[l])
                l += 1
            }
            if r % 2 == 1 {
                r -= 1
                ans = biOpe(ans,tree[r])
            }
            l /= 2
            r /= 2
        }
        return ans
    }
    
    func prtTree(){ // 説明用に追加
        print(tree[1...])
    }
    func prtAry(){ // 説明用に追加
        print(tree[n...])
    }
}

let nums = [7, 2, 10, 4, 5, 1, 3]
let st5 = SegTree(Array(nums[0..<5]))
let st6 = SegTree(Array(nums[0..<6]))
let st7 = SegTree(nums)

st5.prtTree() // [10, 7, 10, 5, 7, 2, 10, 4, 5]
st5.prtAry() // [7, 2, 10, 4, 5]
st6.prtTree() // [10, 10, 7, 10, 5, 7, 2, 10, 4, 5, 1]
st7.prtTree() // [10, 10, 7, 10, 5, 3, 7, 2, 10, 4, 5, 1, 3]

print(st7.query(0,7)) // 10

蛇足

• モノイドって変な言葉だなぁ、モノリスの親戚かな？とアホな事を考えてしまったので、自分なりに、キチンと考えて、以下のように理解した。
  • MONO(単一の) + IDenIdentity element(単位元) を持つ世界。
  • 例えば、乗算なら1が単位元、加算なら0が単位元になるけど、小学校で学ぶ算数は、加算と乗算が同時に行われるため、加算の単位元0も乗算の単位元1も含んでいて、単位元が1つの世界（モノイド）ではない。