Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@kei_tnk

計算量削減の技法（BIT：フェニック木）【競技プログラミング】

Last updated at Posted at 2024-09-09

救済の青汁！師匠も競技プログラミングやってたら面白いな

はじめに

  • ABC370d問題がTLEで解けなかったんだけど、そもそも、データ構造体として順序付集合がないと解くのが厳しかったみたい。
  • で、あいかわらずswiftさんは未対応1だけど、順序付集合を作るのは大変そうなので、代わりとなるフェニック木（BIT:Binary lndexed Treeとも呼ばれる）を導入することとした。ちなみに、フェニックさんが1994年に提唱したアルゴリズムだから、フェニック木と呼ばれる。

フェニック木の配列格納インデックスと格納データの中身

  • 構造体を自作するけど、当然、元データは配列に格納してつくる。過去にヒープを作ったときと同じだね。
  • ヒープの時は、下記の二分木の頂点番号から1を引いた数と配列のインデックスを紐付けてデータ格納をしていた。
  • フェニック木では、下図の番号から1を引いた数と配列のインデックスを紐付けてデータを格納する。
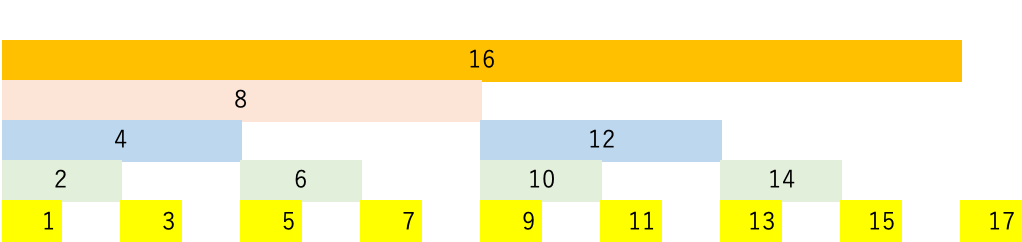
    image.png
  • ちょっと、番号のパターンが複雑だね。奇数が最下層となり、最も左は、上方向に2の累乗となっている。
    • 二層目に着目すると4ずつ増加しており、三層目に着目すると、8ずつ増加している。
    • でも、特徴はそれだけかな？各番号のマスの右端の位置はどうなってるかな？
    • 4(青色のマス)の右端は、原点(左端)から4刻みの位置にあるね。10(緑色のマス)の右端は、原点から10刻みの位置にある。つまり、全てのマスの右端の刻みはマスの番号と一致している。
  • そういえば、データ格納する配列にどんな数値を格納するか説明してなかったね。
  • そもそもで言えば、オリジナルの配列が存在して、それをフェニックス木に変換することとなる。
  • 例えば、オリジナルの配列をA、フェニックス木対応配列をBとすれば、B[0]=A[0]、B[1]=A[0]+A[1]、B[2]=A[2]、B[3]=A[0]+A[1]+A[2]+A[3]となる。
  • つまり、上記図における各番号のマスの幅が、オリジナルの配列の合計範囲となっている。
  • マス6の値は、B[5]に格納されるけど、マス6は図上で5〜6の範囲となっており、これはつまり、オリジナルの配列AのA[4]とA[5]の合計値となる事が分かる。
  • 例えば、オリジナルの配列A=[4,2,6,9,1,0]だったとき、フェニックス木対応配列B=[4,6,6,21,1,0]となる。

そもそもフェニック木とは？

  • 例えばヒープの特徴は、以下の通り。
    • 計算量O(1)で、最大値（または最小値）のデータを取得できる。⇔ 配列ならO(N)
    • データ追加の計算量はO(logN) ⇔　配列なら最後尾追加でO(1)、途中挿入でO(N)
    • ルート（最大値or最小値）の取出し(最大値取得後に削除して、残りの中の最大値が新しくルートになる)の計算量はO(logN) ⇔　配列ならO(N)
  • 配列の特徴として、データ挿入・抜き取り時の計算量がO(N)となり、大きいというのがある。これに対し、ヒープはデータ追加がO(logN)と配列より大きいものの、主な作業でO(logN)となり、O(N)となるような作業がないため高速。そのかわり、出来ない作業もある。例えば、最大ヒープを作った場合、最大値はO(1)で取り出せるが、最小値は取り出せない。
  • フェニックス木は何が得意かというと、合計値の計算がそこそこ得意、かつ、要素の値更新もそこそこ得意である。次は、その点を説明する。

オリジナル配列vs累計和配列vsフェニックス木

  • それぞれ、「値更新(オリジナル配列の任意の1要素の値更新)」「累積和計算」にかかる計算量が異なる。累積和配列については過去の投稿を参考にしてね。
処理 オリジナル配列 累積和配列 フェニック木
値更新 O(1) O(N) O(logN)
累積和計算 O(N) O(1) O(logN)
  • オリジナル配列と累積和配列の計算量については、説明しなくてもピンとくるだろうか？まぁ、大丈夫でしょう。
  • フェニックス木について言えば...
    • 例えば、マス5の「値更新」をすれば、マス6、マス8，マス16の値更新が必要であり、この値更新の回数は最大logN（マス1の値更新が最大回数）となる。勿論、フェニックス木のマスが存在しない、オリジナル配列AのA[5]（フェニックス木のマス5とマス7の間の空欄部分）が更新された場合もフェニックス木のマス6、マス8，マス16の値更新が必要となる。
    • また、「累積和計算」として、例えば、マス11までの累積和は、マス8，マス10、マス11の値合計であり、加算回数は最大logNとなる。上図で言えば、マス15までの累計（マス8+マス12+マス14+マス15）が最大加算回数となる。
  • 上記のとおり、フェニックス木は、「値更新」「累積和計算」において、「オリジナル配列」と「累積和配列」のいいとこ取りをしていると言える。

フェニックス木を自作する

  • これは、上図を参考に、本能の赴くままに作れば楽勝でしょ。と思うじゃん？
  • そんな本能は僕に標準装備されてないから、調べました。
  • 答えを知ってみたら簡単でした。以下、配列インデックス(0スタート)ではなく、マス番号(1スタート)で話を進めるね。
    • 「マス番号奇数」の場合、元データをそのまま格納します。
    • 「マス番号偶数」の場合、ビット表示で右側の「0埋め」されている部分を合計します。
      • そんな説明じゃ分からないよね。ゴメンナサイ。もう少し詳しく説明します。
      • 例えば、マス番号「12」はビット表示で、「1100」になるけど、この「00」部分を変化させて作られるマス番号を合計します。
      • まだ、よく分からないよね。もっとかみ砕くと、「0埋め」部分を下線部のように変化させて作られる「1001」(9)、「1010」(10)、「1011」(11)、「1100」(12)が合計範囲となります。ほら、上図のマス12の横幅と一致してるでしょ？
      • ちなみに、「00」の左隣の「1」について、いったん「0」にして計算してることに留意してね。
  • あ、言い忘れてたけど、フェニックス木の使い道から言うと、ヒープのように要素を追加したリ、削除したりはしないよ。そもそも、オリジナルの配列ありきの配列だし、「累積和」の計算と「値更新」がそれぞれネックにならないようにするのが目的のデータ構造だから、サイズ（要素数）が変動するような使い方は想定していない。
  • さて、上記ルールを元に、コードを書くと以下のとおり。
struct BIT<T:Numeric>{
    var size:Int
    var B:[T]
    
    init(n:Int)
    {
        size = n
        B = [T](repeating:T.zero,count:size)
    }
    init(_ vs:[T]){
        self.init(n:vs.count)
        for i in 0..<vs.count{
            add(i,vs[i])
        }
    }
 
    mutating func add(_ i:Int,_ v:T){
        var i1 = i+1 // インデックス数値に1を足した数値を使う
        while i1 <= size{
            B[i1-1] += v
            i1 += lsb(i1)
        }
    }

    // sum(i)はオリジナル配列A[0]...A[i-1]の合計値とし、i=0のときsum(i)=0とする
    func sum(_ i:Int)->T{ 
        if i == 0 {return 0}
        var i1 = (i+1) - 1
        var sum = T.zero
        while i1 > 0 {
            sum += B[i1-1]
            i1 -= lsb(i1)
        }
        return sum
    }
    
    func lsb(_ i:Int)->Int{ i & -i }
}

let A = [1,2,3,4,5]
var bit = BIT(A)
print(bit) // BIT<Int>(size: 5, B: [1, 3, 3, 10, 5])
print((0...5).map{bit.sum($0)}) // [0, 1, 3, 6, 10, 15]
  • 出来た！
  • 上記コードを見て、「lsbってなんじゃい！」と思う人は、wikiを読んでみて。正直、c++での実装例をパクっただけっす。スマヌ。

使ってみる

5 5 // 配列サイズN=5，クエリー数Q=5
1 2 3 4 5 // 配列の中身
1 0 5 // クエリー種別1(累積和計算) 0..<5の累積和を出力せよ
1 2 4
0 3 10 // クエリー種別0(値更新) 配列[3]の値を10加算せよ
1 0 5
1 0 3
  • 上記の制約は、N,Q≦5*10^5だから、オリジナル配列を使うと、クエリ種別1(累積和計算)で計算量O(N･Q)がTLEとなり、累積和配列を使うと、クエリ種別0(値更新)で計算量O(N･Q)となりTLEとなる。
  • よって、この問題は、フェニック木を使うしかない。
  • これを使って解くと以下のとおり。
struct BIT<T:Numeric>{･･･} // 省略

let (N,Q) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0],$0[1])}[0]
let vs = readLine()!.split(separator:" ").map{Int($0)!}

// フェニック木を生成
var bit = BIT(vs)

for _ in 0..<Q {

    let (a,b,c) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0],$0[1],$0[2])}[0]
    
    if a == 0 {
    // 値変更(加算)クエリ
        bit.add(b,c)
        
    } else {
    // 累積和表示クエリ
        print(bit.sum(c) - bit.sum(b))
        
    }
}
  • 提出したら、1000ms以下で解けました。

応用編...

  • フェニック木の実力は、こんなものじゃない！
  • そもそも、ABC370d問題を解くのに必要な「順序付集合」の代わりに作ったのに、その役に立ってないしね。
  • 遠回りだけど、応用編の話に入る前に、なぜ、「順序付集合」が必要だったのかの確認から入ろうかな？必要性を理解してからの方が、ヤル気が湧くよね？

応用編...に入る前の必要性の確認（ABC370d問題）

  • 問題自体は、計算量を考慮しなければ、全く難しくないよ。内容的には、国民的ゲーム「ボンバーマン」を知っている人なら、すぐに理解できる。
    • 縦H×横Wのマスを用意します。このマスは初期状態では壁で埋まっています。
    • クエリ毎に座標(縦：i , 横:j)が指定されます。
      • 座標位置に壁があれば、壁が破壊されます
      • 座標位置に壁がなければ、座標から上下左右方向に向かって最初にぶつかった壁が破壊されます。
    • クエリ終了後に残った壁の数を答えなさい。
  • 入力例
2 4 3 // 縦2×横4のマス、クエリ3つ
1 2 // 座標(縦1，横2)に爆弾セット
1 2
1 3
  • 計算量を何も考えずに本能の赴くまま解いたコードは以下のとおり。当然、TLEとなった。d問題だから、計算量削減が必要。
let (H,W,Q) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0],$0[1],$0[2])}[0]

extension Array {
    init(_ cnt: Int, _ v: Element) {
        self = [Element](repeating: v, count: cnt)
    }
    init(_ cnt2:Int, _ cnt1:Int, _ v:Int) where Element == [Int] {
        self = [[Int]](cnt2,[Int](cnt1,v))
    }    
}

var HW = [[Int]](H,W,1)

for _ in 0..<Q {
    let (r,c) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0]-1,$0[1]-1)}[0]
    
    if HW[r][c] == 1 {HW[r][c] = 0;continue}
    
    //左爆破
    
        for i in (0...(c-1)).reversed() {
            if HW[r][i] == 1 {HW[r][i] = 0;break}
        }
    
    
    //右爆破
      
        for i in (c+1)..<W {
            if HW[r][i] == 1 {HW[r][i] = 0;break}
        }
    
    
    //上爆破
    
        for i in (0...(r-1)).reversed() {
            if HW[i][c] == 1 {HW[i][c] = 0;break}
        }
    
    
    //下爆破

        for i in (r+1)..<H {
            if HW[i][c] == 1 {HW[i][c] = 0;break}
        }
    
}

print(HW.flatMap{$0}.reduce(0,+))
  • 制約は、「$H×W ≤ 4×10^5$」と「$Q ≤ 2×10^5$」。H×Wが極端に横長のマス(1×W)だった場合、Wは最大$4×10^5$となるから、上記の「左爆破」「右爆破」の計算量は最大$4×10^5$回行われ、それがQ回行われるので、QとWの二重forループで、$8×10^{10}$回のループが出来てしまうから、TLEとなる。
  • じゃあ、計算量を削減しなくちゃね、と言うことで、思い浮かぶのは...何？
    • はい、ニブタンですね。でも､その場合、配列HW[i][j]だと使い物になりません。
    • 例えば、左右爆破で、破壊する壁の位置をニブタンで探索したいなら、壁が残っている位置を格納した配列、例えば、初期状態の後、横位置iが爆破されただけなら、[0,1,2,3,...,j-1,j+1,...,W-1]の様な配列が必要になる。この配列も、爆弾が大量に爆発した後、両端の壁しか残ってない場合は、[1,W-1]のような配列に変化する。
    • このような配列を用意できれば、良い感じのsolve関数を作って、爆破座標から最も近い壁の位置をO(logN)で検索できる。
    • ちなみに、縦位置のニブタン検索用の配列も別途必要となります。
    • 結局必要となる配列は、H本の横方向配列と、W本の縦方向配列となります。
    • でも、1回のクエリ(1回の爆発)で作業が必要な配列は、縦横1本ずつだから、合計の計算量はO(Q･logW + Q･logH)となるはず！これなら、TLEを喰らわないね。
    • よし！この方向性で行こう！...あれ？「順位付集合」は必要ないの？何か見落とした？
    • はい、見落としてます。サイズNの配列から要素を削除するとき、O(N)の計算量が発生します。つまり、爆弾が破裂したとき、横報告の破壊される壁を発見する計算量はO(logW)だとしても、壁を破壊する計算量がO(W)かかってしまいます。
    • なんだか、先ほど解いたFenwick Treeを思い出すね。さっきは、「値更新」と「累積和計算」を良い感じに実行するために、配列の代わりに「フェニック木」を使ったけど、今回は、「要素削除」と「ニブタン」を良い感じに実行するために、配列の代わりに「順序付集合」を使うと言うこと。

具体的に何が必要？

  • 具体的には、「要素削除」と「ニブタン」をそこそこ高速に行うデータ構造が欲しい。
  • そこそこ高速とは、O(1)ほど早くなくても良いけど、O(N)だと遅すぎる、という感じ。まぁ、そんな計算量って、O(logN)しかなさそうだね。
  • c++だと、std::set(順序付集合)が用意されている。swiftにもSet(集合)があるけど、順序がないんだよね。
  • で、c++のstd::setは、要素削除がO(logN)、ニブタン技法を使うlower_boundもO(logN)となっていて、まさにドンピシャ！
  • 同じことをフェニック木でやるのが目的です。

満を持して、応用編！

  • フェニック木では、標準機能として、「値更新」「累積和計算」をやや高速なO(logN)で処理できるaddとsumをもっていた。
  • これに、「要素削除」「ニブタン」をやや高速で処理する機能を追加したい。
  • まず、「要素削除」についてだけど.....あれ？フェニック木では、イニシャライズしたときにサイズが固定されるのでは？と思うじゃん？実は、フェニック木の要素は追加削除しません。じゃあ、どうするかというと、「順序付集合」における要素（ABC370d問題の横方向の初期状態で言えば、[0,1,2,...,W-1]）の値を、サイズWのフェニックス木Bのオリジナル配列Aにおけるインデックス値の0/1と対応させると言うこと。
    • 具体的に言えば、W=5のときの初期状態の順序付集合は[0,1,2,3,4]になるけど、このとき、A=[1,1,1,1,1]になり、その後、爆弾が何度か爆発して、順序付集合が[0,3,4]になったときは、A=[1,0,0,1,1]となっている。ちなみにこの時、B=[1,1,0,2,1]となるよ。
  • これで、「要素削除」は既存関数addを使って、「−1」を加算するだけで実現できると理解したかな？
  • あれ？応用編とは？...いや、まだあわてるような時間じゃない。「ニブタン」が残ってる。
  • さて、「ニブタン」だと意味が広すぎるから、ピンポイントで「lower_bound」にしよう。「lower_bound」って何？と思った人は、過去の投稿を参考にしてね。
    • lower_boundで十分な理由。
      • まず、フェニック木のlower_boundの定義だけど、例えばフェニック木のインスタンスbitに対して、bit.lower_bound(x)で返ってくる値は、「x ≦ ΣA[i]{i in 0...k}」を満たす最小のkの値となる。元々作っていた関数sum(k)は、ΣA[i]{i in 0..<k}でインデックスが1つズレているから、lower_boundの為だけに、新たな関数nsum(k)=ΣA[i]{i in 0...k}を用意する。
      • 通常の配列におけるlower_bound(x)は、sort後配列の要素が最初にx以上となるインデックスだったけど、フェニック木では、オリジナル配列の0...kまでの合計が最初にx以上となるインデックスというのが特徴だね。
      • で、爆破地点から最も近い壁の位置を探るのに「lower_bound」で十分な理由だけど、まず、爆破地点を表すインデックスiにおいて壁が残っているかどうかは、sum(i+1)-sum(i)が1か0可で判定できる。思い出して欲しいのは、sum(i)の意味は、インデックス0..<iの累積和だから、インデックスiにおける壁の有無の情報は入ってないと言うこと。よって、sum(i+1)の情報が必要。
      • で、sum(i+1)-sum(i)が1なら、add(i,-1)して処理は終わり
      • sum(i+1)-sum(i)が0なら、lower_bound(sum(i)+1)がiの先の壁の位置となる。
      • じゃあ、iの手前の壁の位置は？これは簡単で、lower_bound(sum(i))で求められる。
      • ちなみにだけど、オリジナル配列の要素に負数を含まないことが前提だよ。だって、負数が含まれていると、累積和が右肩上がりじゃなくなるからね。右肩上がりであることが、ニブタンの大前提だよ。
  • さて、サクッとlower_boundを実装しますか。勿論、ニブタンを使って実装するよ。関数名は過去の投稿にあわせて、lboundにします。
  • あと、lbound導入に当たって、型ジェネリクスTの制約がNumericの他にComparableも必要になったから､対応するね。struct BIT<T: Numeric & Comparable> {･･･} 
    // nsum(i)はオリジナル配列A[0]...A[i]の合計値。ノーマルな合計値と言うことでnsum
    func nsum(_ i:Int)->T{ 
        var i1 = i+1
        var sum = T.zero
        while i1 > 0 {
            sum += B[i1-1]
            i1 -= lsb(i1)
        }
        return sum
    }
    
    // lower_bound
    func lbound(_ x:T)->Int{

        var ng = -1 // 探索範囲の左端のindexより1小さい
        var ok = (size-1)+1 // 探索範囲の右端のindexより1大きい
        
        while ok - ng > 1 {
            let m = (ng + ok) / 2
            if nsum(m) >= x {ok = m} else {ng = m} 
        }
        
        return ok
    }
  • 実際に動かすと
let A:[Int] = [1,2,3,4,5]
var bit = BIT(A)
print(bit) // BIT<Int>(size: 5, B: [1, 3, 3, 10, 5])
print((0..<bit.size).map{bit.nsum($0)}) // [1, 3, 6, 10, 15]

print(bit.lbound(0)) // 0
print(bit.lbound(1)) // 0
print(bit.lbound(2)) // 1 
print(bit.lbound(3)) // 1
print(bit.lbound(4)) // 2 

print(bit.lbound(9)) // 3 
print(bit.lbound(10)) // 3
print(bit.lbound(11)) // 4

print(bit.lbound(16)) // 5 -- size-1を超えた == 条件を満たすインデックスなし
  • うむ、lboundの役目を果たしてるね。
  • あれ？結局、応用編でやったのは、lboundの実装だけ？
  • いやいやいや、「順序付集合」の代わりにオリジナル配列Aの各indexの値を0/1で集合の値の有無を表すという、アイデアに気付かせたのも応用編の重要な意味だったよ！
  • ついでだから、オリジナル配列の要素を全てvで埋めるイニシャライザも追加しておこう。今回の問題に関して言えば、
  • v=1をオリジナル配列の要素に格納するイメージだね。
    init(n:Int)
    {
        size = n
        B = [T](repeating:T.zero,count:size)
    }
    init(_ vs:[T]){
        self.init(n:vs.count)
        for i in 0..<vs.count{
            add(i,vs[i])
        }
    }
    init(n:Int,v:T){ // 追加したイニシャライザ。今回の問題を解くときは、v=1とする
        self.init(n:n)
        for i in 0..<n{
            add(i,v)
        }        
    }

フェニック木でABC370d問題を解く

  • ここまでの説明で、何をやれば良いか、もう説明済みだから、コードだけ書くね。
struct BIT<T: Numeric & Comparable> {･･･} // 省略

let (H,W,Q) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0],$0[1],$0[2])}[0]

extension Array {
    init(_ cnt: Int, _ v: Element) {
        self = [Element](repeating: v, count: cnt)
    }
}

var H_W = [BIT](H,BIT(n:W,v:1)) // 横方向のBITをH本用意
var W_H = [BIT](W,BIT(n:H,v:1)) // 縦方向のBITをW本用意

func erase(_ r:Int,_ c:Int){
    H_W[r].add(c,-1)// 横方向の壁を消去
    W_H[c].add(r,-1)// 縦方向の壁を消去  
}

for _ in 0..<Q {
    let (r,c) = [readLine()!.split(separator:" ").map{Int($0)!}].map{($0[0]-1,$0[1]-1)}[0]
    
    if W_H[c].sum(r + 1) - W_H[c].sum(r) == 1 {
        erase(r,c)
        continue
    }
    
    
    //左壁爆破
    if H_W[r].sum(c) > 0{
        let lt = H_W[r].lbound(H_W[r].sum(c)) //左：レフト（インデックス0側）
        if 0 <= lt { erase(r,lt) }
    }
    
    //右壁爆破    
    let rt = H_W[r].lbound(H_W[r].sum(c)+1) //右：ライト（インデックスW側）
    if c < rt && rt < W { erase(r,rt) }
    
    //上壁爆破
    if W_H[c].sum(r) > 0{
        let tp = W_H[c].lbound(W_H[c].sum(r)) // 上：トップ（インデックス0側）
        if 0 <= tp { erase(tp,c) }          
    }
    
    //下壁爆破    
    let bm = W_H[c].lbound(W_H[c].sum(r)+1) // 下：ボトム（インデックスH側）
    if r < bm && bm < H { erase(bm,c) }

}

var ans = 0
for i in 0..<H {
    ans += H_W[i].sum(W)
}

print(ans)
  • 提出したら300ms程度でACだった。ちなみに現時点で、他にswiftでACの人はいなかったよ。
  • swift6になったら、swift-collectionsが使えるようになって、OrderedSetが使えるようになるのかな？

おわりに

  • 今回、フェニック木を導入してみた。
  • 実は「セグメント木」の方が汎用的で使い勝手が良いらしいけど、セグメント木は次の機会に頑張るね。
  • それにしても、ABC370はc問題まで楽勝だったから、d問題さえ解ければ初の4完だったのになぁ。残念です。

付録

  • コピペしやすいように、BIT構造体の全体コードを載せておくね。
struct BIT<T: Numeric & Comparable> {
    var size:Int
    var B:[T]
    
    init(n:Int)
    {
        size = n
        B = [T](repeating:T.zero,count:size)
    }
    init(_ vs:[T]){
        self.init(n:vs.count)
        for i in 0..<vs.count{
            add(i,vs[i])
        }
    }
    init(n:Int,v:T){
        self.init(n:n)
        for i in 0..<n{
            add(i,v)
        }        
    }
 
    mutating func add(_ i:Int,_ v:T){
        var i1 = i+1 // インデックス数値に1を足した数値を使う
        while i1 <= size{
            B[i1-1] += v
            i1 += lsb(i1)
        }
    }
 
    // sum(i)はオリジナル配列A[0]...A[i-1]の合計値とし、i=0のときsum(i)=0とする
    func sum(_ i:Int)->T{ 
        if i == 0 {return 0}
        var i1 = (i+1) - 1
        var sum = T.zero
        while i1 > 0 {
            sum += B[i1-1]
            i1 -= lsb(i1)
        }
        return sum
    }
    func lsb(_ i:Int)->Int{ i & -i }
    
    // nsum(i)はオリジナル配列A[0]...A[i]の合計値。ノーマルな合計値と言うことでnsum
    func nsum(_ i:Int)->T{ 
        var i1 = i+1
        var sum = T.zero
        while i1 > 0 {
            sum += B[i1-1]
            i1 -= lsb(i1)
        }
        return sum
    }
    
    // lower_bound
    func lbound(_ x:T)->Int{

        var ng = -1 // 探索範囲の左端のindexより1小さい
        var ok = (size-1)+1 // 探索範囲の右端のindexより1大きい
        
        while ok - ng > 1 {
            let m = (ng + ok) / 2
            if nsum(m) >= x {ok = m} else {ng = m} 
        }
        
        return ok
    }
    
}

  1. Apple謹製のswift-collectionsと言う外部ライブラリには存在（OrderedSet）してて、AtCoderの提出環境でも有効だけど、paiza.io等のオンラインコンパイラでは未対応。 ↩

0
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?