swiftに存在しないデータ構造(スタック、キュー、ヒープ)を自作してみる【競技プログラミング】

はじめに

• データ構造として、配列は使いまくってるけど、スタック、キュー、ヒープもよく競プロの学習書では登場する。でも、swiftには、スタック、キュー、ヒープは存在しないから、自作してみることとする。
• スタックとキューの機能は、配列やCollectionで代用出来るから、あえて自作する必要も無いんだけど、真打ちとして「ヒープ」を自作する前の練習がわりに作ってみる。
• ちなみに、データ構造っていうのは、データ（要素と呼ぶ）の集合の管理手法って感じかな。実際の動きを見た方が分かり易いと思う。いつも使ってる配列もデータ構造の一つだと言えば、なんとなく分かるでしょ？

スタック

• 下図のように、後入れ先出し（LIFO: Last In First OutまたはFILO: First In Last Out）のデータ管理を行う。
  
• 配列を利用して、Int型のみを格納する形で実装するとすれば、こんな感じかな

struct Stack : CustomStringConvertible{ // print文の出力をdescriptionで制御するためのプロトコル

    // 実体は配列
    var data:[Int]
    var description: String { return data.description } // インスタンスのprint文で出力されるもの
    
    init(_ ints:Int...){ // 可変長の整数列を引数として受け取る
        data = Array<Int>(ints)
    }
    
    mutating func push(_ i:Int) {
        data.append(i)
    }

    mutating func pop()->Int? {
        if data != [] {
            return data.removeLast()
        } else {
            return nil
        }
    }    
}

var s = Stack(1,3,5)
print(s.pop()) // Optional(5)
print(s) // [1, 3]
s.push(10)
print(s) // [1, 3, 10]

• これは楽勝だったね。ついでに、インスタンスをprintしたときの見た目を良くするため、初めてCustomStringConvertibleプロトコルを使ってみたよ、

キュー

• 下図のように、先入れ先出し（FIFO: First In First Out）のデータ管理を行う。
  
• 正直、計算量を無視すれば、配列を使って表現したスタックと同様に簡単にコードが書ける。でも、スタックでは、最後尾がpopで取り出されたのと異なり、キューではdequeueにより『先頭』から取り出される。配列の計算量は、最後尾を取り出すときがO(1)なのに対し、先頭から取り出すときはO(n)となってしまい、遅い。配列で無く、Collectionプロトコルに従う構造体であれば、先頭からの取り出しがO(1)ですむので、なんとか、Collection型で実装してみる。

struct Queue : CustomStringConvertible{ // print文の出力をdescriptionで制御するためのプロトコル

    // 実体はコレクション型
    var data:AnyCollection<Int>
    var description: String { return Array(data).description } // インスタンスのprint文で出力されるもの
    
    init(_ ints:Int...){ // 可変長の整数列を引数として受け取る
        data = AnyCollection(Array(ints))
    }

    // deqの計算量O(1)にするため、コレクション型を使ってみたものの、
    // コレクション型の要素追加メソッドが無かったため、配列経由としたから、多分、enqの計算負荷は高い
    mutating func enq(_ i:Int) {
        var newdata = Array(data)
        newdata.append(i)
        data = AnyCollection(newdata)
    }

    // enqの犠牲の上に、deqは計算量O(1)を実現できてるはず！
    mutating func deq()->Int? {
        if !data.isEmpty {
            return data.removeFirst()
        } else {
            return nil
        }
    }    
}

var q = Queue(1,3,5)
print(q) // [1,3,5]
q.enq(10)
print(q.deq()) // Optional(1)
print(q) // [3, 5, 10]

• deqの計算量はO(1)にできたとは思うけど、代わりにenqの計算量が凄いことになってると思う。たかが1データ追加のためにArrayを生成とかアホの極み！まぁ、僕がアホなんだけど...でも、まさかCollectionプロトコルにそもそもデータ追加のメソッドが存在しないとか想定外だったよ。

ヒープ

• 肩が暖まってきたところで、真打ちヒープの実装を行う。
• ヒープについては、先日、志半ばにして実装を断念してしまったので、再チャレンジということになる。
• まぁ、面倒臭くなって、そもそも実装にチャレンジもしてなかったけどね。結論から言えば、思ったよりも簡単だったよ。
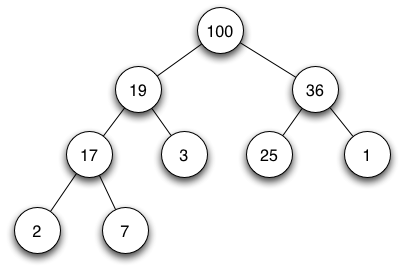
• 下図の「最大ヒープ」について復習すると、以下の通り。
  • 各々のノードはそのノードの子よりも大きいか等しくなるように配置される（ルール①[heap property]）　⇒　当然、根が最大値となる
  • ノードは左から右へ順に埋まっていく（ルール②[shape property]）
    
• 実装は、「最小ヒープ」「最大ヒープ」を選択できるように行う事とする。下記の解説は、「最大ヒープ」の前提で記載する。
• 各ノードの番号は、親の番号iに対して、左下が2i、右下が2i+1の関係にすると、綺麗にノード番号が重ならず埋まっていく。なお、最上位のノード（ノード番号1）を根(ルート)と呼ぶ。ちなみに子の番号iに対して、親の番号はi/2(余りは切り捨て)となる。
  
• また、要素の格納先として、1次元配列を利用する。配列は、「インデックスを利用した要素へのアクセス(値の取得･変更)」や「最後尾への要素追加･削除」が計算量O(1)で出来るため、ヒープの値格納先として不都合がない。なお、ノードの番号を1から開始する形で説明したけど、配列に格納するときのindexは0から始まるので1ズレることに注意する。
• 実装の方針として、「要素の追加」「根の値変更」「根の取出し」のみ対応することとする。
  • 要素の追加(.insert(Int))
    • 配列の最後尾に追加する
    • 親ノードの値と比較して必要に応じて入れ替える（以下ループ）
  • 根の値変更(.chgRoot(Int))
    • 根の値を変更する
    • 子ノードの値と比較して必要に応じて入れ替える（以下ループ）
      • 入れ替える場合、子ノードの内、大きい方と入れ替える
  • 根の取出し(.popRoot()->Int?)
    • 根の値を取得する
    • 配列最後尾を削除するとともに、その値を根の値に上書きする
    • 以降、「根の値変更」と同じ
• 上記の実装方針を読むと分かるとおり、「要素の追加」「根の値変更」「根の取出し」のどれを行っても、最大の作業回数（ノードの値の親子交換）は、2分木の高さ(logN[底:2])となる。よって、最小値や最大値を取り出したいだけのデータ構造として、計算量が少ないヒープは適している。

struct Heap : CustomStringConvertible { // print文の出力をdescriptionで制御するためのプロトコル

    // 実体は配列
    private var data:[Int] = [] //　初期値はブランク
    var description: String { return data.description } // インスタンスのprint文で出力されるもの
    
    // 最大ヒープ(true)か最小ヒープ(false)かを選択するBool（初期値はtrue）
    private var maxHeap:Bool
    
    init(_ maxHeap :Bool = true){
        self.maxHeap = maxHeap
    }
    

    ///
    ///親インデックスや子インデックスを取得するための関数
    ///
    private func pIndex(_ index:Int) -> Int { //親ノードが格納されているindex
        return (index + 1) / 2 - 1
    }
    
    private func s0Index(_ index:Int) -> Int? { //子ノード(左)が格納されているindex
        let s0 = 2 * (index + 1) - 1
        if s0 < data.count {
            return s0
        } else {
            return nil
        }
    }
    
    private func s1Index(_ index:Int) -> Int? { //子ノード(右)が格納されているindex
        let s1 = 2 * (index + 1)
        if s1 < data.count {
            return s1
        } else {
            return nil
        }
    }
    
    ///大小比較する関数
    func gt(_ l:Int,_ r:Int)->Bool{ // greater thanよりgt
        return (l >= r ? maxHeap : !maxHeap )
    }
    
    ///
    ///メソッド
    ///
    
    //要素の追加
    mutating func insert(_ i:Int) {
        data.append(i)
        var index = data.count - 1
        var value = i
        while index > 0 {
            let pindex = pIndex(index)
            let pValue = data[pindex]
            if gt(pValue,value) {return} // 親の方が大きければ終了
            data[index] = pValue
            data[pindex] = value
            index = pindex
        }
        
    }

    //根の値変更
    mutating func chgRoot(_ i:Int) {
        var index = 0 //根のindex
        var value = i
        data[index] = value // 根を塗り替え
        while true {
            guard let s0index = s0Index(index) else {return} //子ノードが無ければ終了
            let s0Value = data[s0index]
            guard let s1index = s1Index(index) else { // 子ノードがs0のみの時、s0とのみ比較する
                if gt(value,s0Value) {return} // 子ノードの方が小さければ終了
                data[index] = s0Value
                data[s0index] = value
                return // s1が無いとき、下層ないためここで終了
            }
            let s1Value = data[s1index]
            let (sValue,sindex) = gt(s0Value,s1Value) ? (s0Value,s0index) : (s1Value,s1index)
            if gt(value,sValue) {return} // 子ノードの方が小さければ終了
            data[index] = sValue
            data[sindex] = value
            index = sindex
        } 
    }    
    
    //根の取出し
    mutating func popRoot()->Int? {
        if data == [] {
            return nil        
        } else {
            let ans = data[0]
            let last = data.removeLast()
            if data.count > 0 {
                chgRoot(last)
            }
            return ans
        }
    }    
}

var h = Heap()
h.insert(5)
h.insert(10)
h.insert(100)
h.insert(200)
h.insert(-10)
h.insert(20)
print(h) // [200, 100, 20, 5, -10, 10] -- 図①

h.chgRoot(1)
print(h) // [100, 5, 20, 1, -10, 10] -- 図②

h.popRoot() // Optional(100)
print(h) // [20, 5, 10, 1, -10] -- 図③

• 作ってみたけど、正しいかどうか、何でチェックすればいいんだろ？一応、図①,図②,図③を見ると合ってるっぽいけどね。
  
  chgRoot(1)の後
  
  popRoot()の後
  
• 最小ヒープを試してみたら、こんな感じ。

var h = Heap(false) // falseを入れて、最小ヒープにした
h.insert(5)
h.insert(10)
h.insert(100)
h.insert(200)
h.insert(-10)
h.insert(20)
print(h) // [-10, 5, 20, 200, 10, 100] --　図④

h.chgRoot(1)
print(h) // [1, 5, 20, 200, 10, 100] --  図⑤

h.popRoot()
print(h) // [5, 10, 20, 200, 100] -- 図⑥

• 図④,図⑤,図⑥を見ても、合ってるっぽいね。
  
  
  

おわりに

• とりあえず、目標としていたヒープを作れたから、良かった。
• 次は、このヒープをダイクストラ法に導入して、計算量を削減しなければ。 ⇒ yatta!

おまけ

• ヒープのコードをもう少し一般化した。Intだけじゃ無く、Int64もいけるよ！Comparableプロトコルに準拠してる型ならOK（Stringも可）!また、初期化時に適当な順番で値をぶち込んでヒープを作れるようにした。isEmptyとcountも付けちゃうぞ！

struct Heap<V:Comparable> : CustomStringConvertible { // print文の出力をdescriptionで制御するためのプロトコル

    // 実体は配列
    private var data:[V] = [] //　初期値はブランク
    var description: String { return data.description } // インスタンスのprint文で出力されるもの
    
    // 最大ヒープ(true)か最小ヒープ(false)かを選択するBool（初期値はtrue）
    private var maxHeap:Bool
    
    init(_ vs:[V] = [], maxHeap :Bool = true){
        self.maxHeap = maxHeap
        if vs.count > 0 {data += vs;build()}
    }
    

    ///
    ///親インデックスや子インデックスを取得するための関数
    ///
    private func pIndex(_ index:Int) -> Int { //親ノードが格納されているindex
        return (index + 1) / 2 - 1
    }
    
    private func s0Index(_ index:Int) -> Int? { //子ノード(左)が格納されているindex
        let s0 = 2 * (index + 1) - 1
        if s0 < data.count {
            return s0
        } else {
            return nil
        }
    }
    
    private func s1Index(_ index:Int) -> Int? { //子ノード(右)が格納されているindex
        let s1 = 2 * (index + 1)
        if s1 < data.count {
            return s1
        } else {
            return nil
        }
    }
    
    ///大小比較する関数
    func gt(_ l:V,_ r:V)->Bool{ // greater thanよりgt
        return (l >= r ? maxHeap : !maxHeap )
    }
    
    ///
    ///メソッド
    ///
    
    // ヒープ化前の配列をヒープ化
    mutating func build(){
        for n in (0...(data.count / 2)).reversed() {
            heapify(n)
        }
    }
    
    
    //要素の追加
    mutating func insert(_ i:V) {
        data.append(i)
        var index = data.count - 1
        var value = i
        while index > 0 {
            let pindex = pIndex(index)
            let pValue = data[pindex]
            if gt(pValue,value) {return} // 親の方が大きければ終了
            data[index] = pValue
            data[pindex] = value
            index = pindex
        }
    }

    mutating func heapify(_ n:Int){
        var index = n
        var value = data[index]
        while true {
            guard let s0index = s0Index(index) else {return} //子ノードが無ければ終了
            let s0Value = data[s0index]
            guard let s1index = s1Index(index) else { // 子ノードがs0のみの時、s0とのみ比較する
                if gt(value,s0Value) {return} // 子ノードの方が小さければ終了
                data[index] = s0Value
                data[s0index] = value
                return // s1が無いとき、下層ないためここで終了
            }
            let s1Value = data[s1index]
            let (sValue,sindex) = gt(s0Value,s1Value) ? (s0Value,s0index) : (s1Value,s1index)
            if gt(value,sValue) {return} // 子ノードの方が小さければ終了
            data[index] = sValue
            data[sindex] = value
            index = sindex
        }       
    }


    //ノードの値変更
    mutating func chgNode(_ i:V,_ n:Int) {
        data[n] = i // 値塗り替え
        heapify(n)
    }    
    
    // 根の値変更
    mutating func chgRoot(_ i:V){
        chgNode(i,0)
    }
    
    
    //根の取出し
    mutating func popRoot()->V? {
        if data == [] {
            return nil        
        } else {
            let ans = data[0]
            let last = data.removeLast()
            if data.count > 0 {
                chgRoot(last)
            }
            return ans
        }
    }

        // countプロパティを追加
    var count:Int {data.count}     
    
        // isEmptyプロパティを追加
    var isEmpty:Bool {data.isEmpty} 
    
}
let vs0 = [1,2,3,4,5,6,7,8,9,10]
let vs1 = ["c", "b", "a", "C", "B", "A", "4", "3", "2", "1"]// 降順
var h0 = Heap(vs0) 
print(h0) // [10, 9, 7, 8, 5, 6, 3, 1, 4, 2]
var h1 = Heap(vs1,maxHeap:false)
print(h1) // ["1", "2", "4", "3", "B", "A", "a", "c", "C", "b"]

• 文字列を最小ヒープで初期化した結果。合ってるっぽいね。
  
• ついでに、タプルの第1要素の大小でヒープを作るコードもつくってみた。これは、ダイクストラ法で使うことが多いと思うから、最小ヒープをデフォとした。ここで作ったヒープの汎用化だね。

struct HeapTpl<V:Comparable,T:Equatable> : CustomStringConvertible { // print文の出力をdescriptionで制御するためのプロトコル

    // 実体は配列
    private var data:[(V,T)] = [] //　初期値はブランク
    var description: String { return data.description } // インスタンスのprint文で出力されるもの
    
    // 最大ヒープ(true)か最小ヒープ(false)かを選択するBool（初期値はfalse）
    private var maxHeap:Bool
    
    init(_ vs:[(V,T)] = [], maxHeap :Bool = false){
        self.maxHeap = maxHeap
        if vs.count > 0 {data += vs;build()}
    }
    

    ///
    ///親インデックスや子インデックスを取得するための関数
    ///
    private func pIndex(_ index:Int) -> Int { //親ノードが格納されているindex
        return (index + 1) / 2 - 1
    }
    
    private func s0Index(_ index:Int) -> Int? { //子ノード(左)が格納されているindex
        let s0 = 2 * (index + 1) - 1
        if s0 < data.count {
            return s0
        } else {
            return nil
        }
    }
    
    private func s1Index(_ index:Int) -> Int? { //子ノード(右)が格納されているindex
        let s1 = 2 * (index + 1)
        if s1 < data.count {
            return s1
        } else {
            return nil
        }
    }
    
    ///大小比較する関数
    func gt(_ l:(V,T),_ r:(V,T))->Bool{ // greater thanよりgt
        return (l.0 >= r.0 ? maxHeap : !maxHeap )
    }
    
    ///
    ///メソッド
    ///
    
    // ヒープ化前の配列をヒープ化
    mutating func build(){
        for n in (0...(data.count / 2)).reversed() {
            heapify(n)
        }
    }
    
    
    //要素の追加
    mutating func insert(_ v:V,_ t:T) {
        data.append((v,t))
        var index = data.count - 1
        var value = (v,t)
        while index > 0 {
            let pindex = pIndex(index)
            let pValue = data[pindex]
            if gt(pValue,value) {return} // 親の方が大きければ終了
            data[index] = pValue
            data[pindex] = value
            index = pindex
        }
    }

    // 下方向のみ対応
    mutating func heapify(_ n:Int){
        var index = n
        var value = data[index]
        while true {
            guard let s0index = s0Index(index) else {return} //子ノードが無ければ終了
            let s0Value = data[s0index]
            guard let s1index = s1Index(index) else { // 子ノードがs0のみの時、s0とのみ比較する
                if gt(value,s0Value) {return} // 子ノードの方が小さければ終了
                data[index] = s0Value
                data[s0index] = value
                return // s1が無いとき、下層ないためここで終了
            }
            let s1Value = data[s1index]
            let (sValue,sindex) = gt(s0Value,s1Value) ? (s0Value,s0index) : (s1Value,s1index)
            if gt(value,sValue) {return} // 子ノードの方が小さければ終了
            data[index] = sValue
            data[sindex] = value
            index = sindex
        }       
    }


    //ノードの値変更（下方向のみ対応だから、minヒープの時は、親ノードより大きい値のみしか入れられない）
    mutating func chgNode(_ v:V,_ t:T,_ n:Int) {
        data[n] = (v,t) // 値塗り替え
        heapify(n)
    }    
    
    // 根の値変更
    mutating func chgRoot(_ v:V,_ t:T){
        chgNode(v,t,0)
    }
    
    
    //根の取出し
    mutating func popRoot()->(V,T)? {
        if data.isEmpty {
            return nil        
        } else {
            let ans = data[0]
            let (v,t) = data.removeLast()
            if data.count > 0 {
                chgRoot(v,t)
            }
            return ans
        }
    }    
    
        // countプロパティを追加
    var count:Int {data.count}     
    
        // isEmptyプロパティを追加
    var isEmpty:Bool {data.isEmpty} 
    
}

var h = HeapTpl<UInt64,Int>()
print(h.isEmpty) // true
h.insert(5,1)
print(h.isEmpty) // false
h.insert(10,2)
h.insert(100,3)
h.insert(200,4)
h.insert(50,5)
h.insert(20,0)
print(h) // [(5, 1), (10, 2), (20, 0), (200, 4), (50, 5), (100, 3)]

h.chgRoot(55,1)
print(h) // [(10, 2), (50, 5), (20, 0), (200, 4), (55, 1), (100, 3)]

h.popRoot()
print(h) // [(20, 0), (50, 5), (100, 3), (200, 4), (55, 1)]