遅延評価セグメント木について【競技プログラミング】

はじめに

• 配列のとある区間の最大値を求めたり合計値を求めたりする作業（区間取得クエリと呼ぶ）を高速化するテクニックにセグメント木がある。
• このセグ木を使わずに、普通にコードを書くと、サイズNの配列の最大値や合計値を求めるのにO(N)の計算量が必要なところ、セグ木を使うと、O(logN)の計算量で済む。その代わり、配列中の１つの要素の値を塗り替えるとき、普通の配列なら、O(1)の計算量であるところ、セグ木の場合は１つの要素の値の塗り替え(コード上はupdateと表現することが多い)でもO(logN)の計算量が必要となる。
• このように、配列の要素の塗り替えは、セグ木は得意ではないけど、塗り替えを高速化したい場面はあったりする。
• 今回、記事の対象となる「遅延評価セグメント木」（以降、遅延セグ木）は、「配列のとある区間(l..<r)に対して、一様に値を変更させる作業（区間変更クエリと呼ぶ）をしたいときに高速化を図るアルゴリズム」です。

遅延セグ木のカラクリ

• セグ木は裏では配列を使っていました。過去の投稿で使った図では、区間取得クエリの対象配列は、マス16〜31（以降、対象配列と呼ぶ）に格納されていて、マス1〜15(以降、上部ノードと呼ぶ)には、クエリの内容に応じた数値が入ってました。
  • 例えば、マス16と17に入っている数値が「5」と「7」だったとき、その上にあるマス8に入る値は何か？
    • 最小値クエリなら「5」が入り、合計クエリなら「12」が入ります。
      
• 遅延セグ木では、区間変更クエリを高速に行うことになりますが、上図のマス16〜31の値をn個更新しようとすると、どうしてもO(n)の計算量を消費してしまうので、実際には、セグ木の上部ノードと同じようなマスを用意し、区間変更で実際に値を更新するマスは上部ノードにとどめ、対象配列自身は殆ど変更しません。
• 「遅延評価」が頭に付いているのは、区間変更クエリ後の配列の値を知りたいとき、クエリ作業とは別に、値取得のために別途O(logN)の計算量を消費して評価するからだろうね。
• ちなみに、遅延セグ木の説明として定番とお噂のアルメリアさんの記事「AtCoder LibraryのLazy Segtreeの使い方」では、遅延セグ木が下記のように表現されています。
  
• dataが通常のセグ木の値が入る部分で、lazyが遅延セグ木用に追加された部分です。だから、遅延セグ木の構造体を作ろうとしたら、セグ木の構造体のプロパティ「tree」配列と同型の配列（例えば、lazyと命名）を追加する必要があるね。
• そして区間変更クエリと、区間取得クエリを実施したときの値の塗替えの流れをアルメリアさんは下図で説明されてます。
  
• 上記図について、アルメリアさんは、「ある広い区間に対して何度も操作クエリが行われた時、それを末端のノードまで毎回伝えていくと計算量が増えてしまいます。なのでノード全体を覆うような操作はそのノードがずっと溜めておいて、その中のより狭い区間に対するクエリが来たときに初めて下に伝えていく。これが遅延伝播の仕組みです。」と書かれています。
• 例えば、この遅延セグ木の区間取得クエリが「合計クエリ」だったに、区間変更クエリとして「区間のすべての値に３を加算しろ!」と指示した場合、図の左のてっぺんの赤いマスのlazyには「3」を格納し、dataは4マス分カバーする上位ノードのマスだから元の値に12（＝「3」×4マス分）を加算し、他のマス（白いマス）の値は変更しない。そして、例えば、区間取得クエリとして、一番左の１マスだけの合計クエリを実行するとき、図の右側の赤矢印と青矢印の通り、必要に応じて、値を塗り替えていくということなのね。
• ここまで聞いて気がついた人もいるかと思うけど、区間取得クエリが１種類だけ設定できたのと同じように、区間変更クエリも１種類だけ設定できます。
  • つまり、実際に利用する具体的な普通のセグ木について、「区間和クエリ」のセグ木、などと表現されるように、実際に利用する場合の具体的な遅延セグ木も、「区間加算クエリ・区間和クエリ」の遅延セグ木、などと呼ばれることとなります。

具体的な遅延セグ木の作り方（「区間加算」「区間合計」の場合）

• セグ木の構造体は既に作って有るから、それに接ぎ木をするような感じかな？
• セグ木の具体的なコード（合計値クエリ版）はコレ。

class SegTree {
    private var tree: [Int]
    private var n: Int
    private var base: Int = 0
    private var biOpe: (_ l: Int, _ r: Int) -> Int = (+)
    var top :Int {tree[1]} // treeの最上位を返す

    init(_ nums: [Int]){
        self.n = nums.count
        self.tree = Array(repeating: 0, count: 2 * n)
        buildTree(nums)
    }
    convenience init(_ n:Int,v: Int = 0){
        let nums = [Int](repeating:v,count:n)
        self.init(nums)
    }


    // func biOpe(_ l:Int,_ r:Int)->Int{ 
    //     return max(l,r) // クラスプロパティで代入することにしました。
    // }
    func biOpe(_ i:Int)->Int{ // 引数1つのときの関数オーバーロード
        return biOpe(tree[2*i],tree[2*i+1])
    }

    private func buildTree(_ nums: [Int]) {
        for i in 0..<n {
            tree[i + n] = nums[i]
        }
        for i in stride(from: n - 1, through: 1, by: -1) {
            tree[i] = biOpe(i)
        }
    }

    func update(_ index: Int, _ value: Int) {
        var i = index + n
        tree[i] = value
        while i > 1 {
            i /= 2
            tree[i] = biOpe(i)
        }
    }

    func query(_ left: Int, _ right: Int) -> Int {
        var l = left + n
        var r = right + n
        var ans = base
        while l < r {
            if l % 2 == 1 {
                ans = biOpe(ans,tree[l])
                l += 1
            }
            if r % 2 == 1 {
                r -= 1
                ans = biOpe(ans,tree[r])
            }
            l /= 2
            r /= 2
        }
        return ans
    }
    
    func prtTree(){ // 説明用に追加
        print(tree[1...])
    }
    func prtAry(){ // 説明用に追加
        print(tree[n...])
    }
}

// 初期配列の定義
let initialArray = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
let segTree = SegTree(initialArray)

// // 初期状態のセグメント木を表示
print("初期状態のセグメント木:")
segTree.prtTree()
segTree.prtAry()

// // 区間合計クエリ 1..<5 の範囲を合計
let initialSum = segTree.query(1, 5)
print("区間 [1, 5) の初期合計値: \(initialSum)")

初期状態のセグメント木:
[55, 37, 18, 34, 3, 7, 11, 15, 19, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
区間 [1, 5) の初期合計値: 14

• 上記に区間変更クエリとして、加算クエリを設定して作成した遅延セグ木のコードは以下になります。

import Foundation // prtTree等でStringのformat引数を使用するために必要

class LazySegTree {
    private var tree: [Int]
    private var lazy: [Int]
    private var n: Int
    private var base: Int = 0
    private var biOpe: (_ l: Int, _ r: Int) -> Int = (+)
    var top: Int { tree[1] }

    init(_ nums: [Int]) {
        // self.sz = nums.count
        let sz = nums.count
        n = 1
        while n < sz { n *= 2 }
        self.tree = Array(repeating: 0, count: 2 * n)
        self.lazy = Array(repeating: 0, count: 2 * n)
        buildTree(nums)
    }

    convenience init(_ n: Int, v: Int = 0) {
        let nums = [Int](repeating: v, count: n)
        self.init(nums)
    }

    private func buildTree(_ nums: [Int]) {
        let sz = nums.count
        for i in 0..<sz {
            tree[i + n] = nums[i]
        }
        for i in stride(from: n - 1, through: 1, by: -1) {
            tree[i] = tree[2 * i] + tree[2 * i + 1]
        }
    }

    private func eval(_ k: Int, _ l: Int, _ r: Int) {
        if lazy[k] != 0 {
            tree[k] += lazy[k]
            if r - l > 1 {
                lazy[2 * k] += lazy[k] / 2
                lazy[2 * k + 1] += lazy[k] / 2
            }
            lazy[k] = 0
        }
    }

    func add(_ a: Int, _ b: Int, _ x: Int, _ k: Int = 1, _ l: Int = 0, _ r: Int = -1) {
        var r = r
        if r < 0 { r = n }
        eval(k, l, r)
        if b <= l || r <= a { return }
        if a <= l && r <= b {
            lazy[k] += (r - l) * x
            eval(k, l, r)
        } else {
            add(a, b, x, 2 * k, l, (l + r) / 2)
            add(a, b, x, 2 * k + 1, (l + r) / 2, r)
            tree[k] = tree[2 * k] + tree[2 * k + 1]
        }
    }

    func query(_ a: Int, _ b: Int, _ k: Int = 1, _ l: Int = 0, _ r: Int = -1) -> Int {
        var r = r
        if r < 0 { r = n }
        eval(k, l, r)
        if b <= l || r <= a { return base }
        if a <= l && r <= b { return tree[k] }
        let vl = query(a, b, 2 * k, l, (l + r) / 2)
        let vr = query(a, b, 2 * k + 1, (l + r) / 2, r)
        return vl + vr
    }

    func prtIndex() {
        let nums = (1..<(2*n)).map { String(format: "%2d", $0) }.joined(separator: ",")
        print("(",nums,")")
        // print(tree[1...])
    }    
    
    func prtTree() {
        let nums = tree[1...].map { String(format: "%2d", $0) }.joined(separator: ",")
        print("[",nums,"]")
        // print(tree[1...])
    }
    func prtLazyTree() {
        let nums = lazy[1...].map { String(format: "%2d", $0) }.joined(separator: ",")
        print("[",nums,"]")
        // print(lazy[1...])
    }

    func prtAry() {
        let nums = tree[n...].map { String(format: "%2d", $0) }.joined(separator: ",")
        print("[",nums,"]")    
        // print(tree[n...])
    }
}

• 実行例

// 初期配列の定義
let initialArray = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
let segTree = LazySegTree(initialArray)

// 説明
let str = """
1行目：セグ木のインデックス(1スタート)
2行目：セグ木の要素(tree)
3行目：セグ木の遅延要素(lazy)
4行目：評価対象配列の要素(tree[n...]、0-idxだから1行目のインデックスとは1ズレる)

""" 
print(str)


// 初期状態のセグメント木を表示
print("初期状態のセグメント木:")
segTree.prtIndex()
segTree.prtTree()
segTree.prtLazyTree()
segTree.prtAry()

// 区間合計クエリ 1..<5 の範囲を合計
let initialSum = segTree.query(1, 5)
print("区間 [1, 5) の初期合計値: \(initialSum)\n")

// 区間加算クエリ 0..<4の範囲で10を加算
print("区間加算クエリ 0..<4の範囲で10を加算")
segTree.add(0,4,10)

// 加算後のセグメント木を表示（遅延評価前）
print("加算後、遅延評価前のセグメント木:")
segTree.prtIndex()
segTree.prtTree()
segTree.prtLazyTree()
segTree.prtAry()
print()

// 加算後のセグメント木の範囲合計
let addedSum = segTree.query(3,5)
print("区間 [3, 5) の加算後合計値: \(addedSum)")

// 加算後のセグメント木を表示（遅延評価後）
print("区間 [3, 5) の合計クエリ後のセグメント木:")
segTree.prtIndex()
segTree.prtTree()
segTree.prtLazyTree()
segTree.prtAry()
print()

• 上記の出力

1行目：セグ木のインデックス(1スタート)
2行目：セグ木の要素(tree)
3行目：セグ木の遅延要素(lazy)
4行目：評価対象配列の要素(tree[n...]、0-idxだから1行目のインデックスとは1ズレる)

初期状態のセグメント木:
(  1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31 )
[ 55,36,19,10,26,19, 0, 3, 7,11,15,19, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 0, 0, 0, 0, 0, 0 ]
[  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
[  1, 2, 3, 4, 5, 6, 7, 8, 9,10, 0, 0, 0, 0, 0, 0 ]
区間 [1, 5) の初期合計値: 14

区間加算クエリ 0..<4の範囲で10を加算
加算後、遅延評価前のセグメント木:
(  1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31 )
[ 95,76,19,50,26,19, 0, 3, 7,11,15,19, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 0, 0, 0, 0, 0, 0 ]
[  0, 0, 0, 0, 0, 0, 0,20,20, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
[  1, 2, 3, 4, 5, 6, 7, 8, 9,10, 0, 0, 0, 0, 0, 0 ]

区間 [3, 5) の加算後合計値: 19
区間 [3, 5) の合計クエリ後のセグメント木:
(  1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31 )
[ 95,76,19,50,26,19, 0,23,27,11,15,19, 0, 0, 0, 1, 2,13,14, 5, 6, 7, 8, 9,10, 0, 0, 0, 0, 0, 0 ]
[  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,10,10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
[  1, 2,13,14, 5, 6, 7, 8, 9,10, 0, 0, 0, 0, 0, 0 ]

• 解説します。
  • まず、最初に説明すべき変更点は、nの変更。元のセグ木では、nは分析対象の配列の要素数としてたよ。でも、遅延セグ木では、nは分析対象の配列の要素数をカバーする2の累乗としてます。例えば、分析対象の配列の要素数が10だとすれば、それをカバーする2の累乗である16となります。上記実行例が正にそのケース（配列要素数10）です。
    • nを2の累乗とする理由は、「遅延セグ木では、葉からの上昇方向（区間取得エリ）だけでなく、上位ノードから葉に向かう下降方向の動き(区間変更後の伝播)があるから」です。
    • 詳しい話は省くけど、セグ木を頭でイメージするとき、葉の数が2の倍数の方が綺麗な形になることは分かるよね。綺麗な形だと、ノードkの子のノードが2kと2k+1と表現できて、楽なんです。
    • 分析対象配列initialArrayをlet initialArray = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]として、let segTree = LazySegTree(initialArray)のように遅延セグ木を生成したとき、セグ木上の分析対象の配列（要素10個）の格納場所は、下図の黄色部分です。なお、下図の区間[1,5)は配列initialArrayの1..<5なので、合計値は2+3+4+5より14です。
      
      
      
  • 次に、add関数とeval関数の追加について説明します。add関数は、区間変化クエリとして、加算クエリを実行するものです。また、再帰関数になってます。
    
    • add(a,b,x)で、分析対象配列の区間a..<bに対して、xを加算します。ちなみに、分析対象配列a..<bはセグ木のインデックスで言えば、n+a..<n+bになります。
    • なお、前述の通り、分析対象の配列の要素数が10個だった場合も、nは16になります。
    • さて、addのコードを見ると、再帰関数になっていることが分かります。そして、引数は実は3つ(a,b,x)だけでなく、6つ（k,l,rが追加）あることが分かります。なお、再帰関数において(a,b,x)は固定され、(k,l,r)が変化していきます。詳細は後述します。
    • なお、kは上位ノードのインデックスを指し、l,rは上位ノードkがカバーする分析対象単体の範囲を指します。
    • 再帰関数の初回における(k,l,r)はパラメータが指定されないので、(1,0,n)が入力されます。k=1は、セグ木の根となるインデックス。(l,r)=(0,n)は分析対象単体の全範囲(0..<n)に相当します。
    • 再帰関数を見ると、次の周回では、k=2,3、その次の周回では、k=4,5,6,7、となり、セグ木を1段ずつ降りていくことが分かります。
    • add関数が具体的に何をするかの説明の前にeval関数について説明します。
    • eval関数が行っていることは単純です。
      • lazy[k]に入っている値をtree[k]に加算する。
      • lazy[k]が葉(r-l = 1)でない場合
        • 子ノードである、lazy[2k]、lazy[2k+1]に値を半分ずつ分け与える。
      • 最後に、lazy[k]をゼロクリアする。
    • さて、add(0,4,10)の実行について解説します。
      • 結論から言えば､実行後のセグ木の中身は下図のとおりです。
        
      • lazy[8]とlazy[9]にそれぞれ20が入ります。また、tree[1],tree[2],tree[4]で40が加算されています。何も変わりません。
    • add(0,4,10)が行う事をコードに沿って説明します。コードには、緑文字と赤文字で解説を書き込んでるので、適宜読んでください。
      • まず、セグ木の影響範囲を緑の網掛けで示します。また、add関数は、㋐〜㋔の順番でセグ木(treeとlazy)に作用します。
        
      • ㋐では緑の網掛けとマス1が部分的に重なっているので、if文③が適用されます。
        • つまり、再帰関数として㋑（ノード2,3）に移行します。
        • マス3は全く重ならず、lazy[3]もゼロなので無視します。
        • マス2は重なっているので、再帰関数として㋒（ノード4,5）に移行します。
          • マス5は全く重ならず、lazy[5]もゼロなので無視します。
          • マス4は網掛けに含まれているので、if文②が適用されます。
          • よって、初めてlazy配列の値が更新されます。具体的にはlazy[4]に40(=加算10×4マス)が格納されます。
          • その後、eval関数により、tree[4]にlazy[4]の値40が加算され、lazy[4]の子ノードlazy[8],lazy[9]に40の半分20がそれぞれ加算された後、lazy[4]の値がゼロクリアします。
          • ここで、㋐⇒㋔に向かうセグ木の降下は終わり、次は㋔⇒㋐の戻りが実施されます。
          • 戻りとは、具体的にはtreeの再計算です。
        • ㋑の段に戻り、tree[2]=tree[4]+tree[5]を再計算し、tree[4]の変更内容がtree[2]に反映します。
      • ㋐の段に戻り、tree[1]=tree[2]+tree[3]を再計算し、tree[2]の変更内容がtree[1]に反映します。
      • 現場からは以上です。
  • 以上で、add関数とeval関数については、分かって貰えたと思う。
  • 続いて、query関数を説明するよ。
    
  • query(a,b)で、分析対象配列の区間a..<bの合計値を出すよ。まぁ、query関数は普通のセグ木にも有ったから分かるよね。
  • さて、このqueryのコードを見ると、addと似たような再帰関数になっているね。引数として、(k,l,r)が追加されてる。
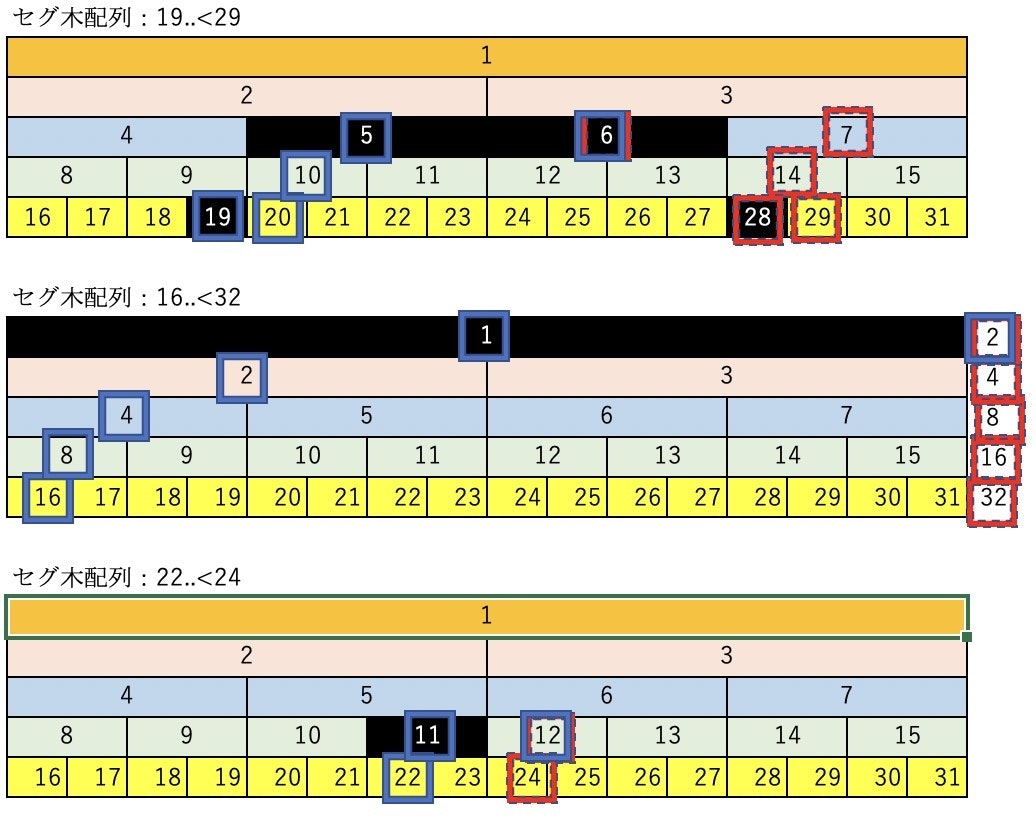
  • 具体的な動作検証として、query(3,5)の実行について解説します。
    • 結論から言えば、実行後のセグ木の中身は下図の通りです。
      
    • lazy[8],lazy[9]が20から0に変わり、tree[8],tree[9]がそれぞれ20加算されてます。
    • tree[18],tree[19]がそれぞれ10加算されています。なお、青い下線部分は、セグ木の葉部分であり、評価対象配列が格納された部分です。つまり、評価対象配列をnumsと考えたとき、nums[2],nums[3]は遅延評価が完了したと言えます。
    • lazy配列は、マス16,17がまだ残ってます。「既に葉部分なのだからtreeに反映して、遅延評価を残しておくなよ」と思わなくもないですが、少しでも計算量を減らすため、必要ないことを回避するのが遅延セグ木の流儀。
  • query(3,5)が行う事をコードに沿って説明します。
    • まず、セグ木の営業範囲を青の網掛けで示します。
      
    • ㋐では青の網掛けとマス1が部分的に重なっているので、if文①②を通り抜けて、再帰関数ゾーンに入ります。つまり、㋑(ノード2,3)に移行します。
    • マス3は全く重ならず、lazy[3]もゼロなので無視します。
    • マス2は重なっているので、再帰関数として㋒(ノード4,5)に移行します。
      • ノード4経由の㋓への移行
        • ノード8は、lazy[8]がゼロではないから、値を同マスのtreeに加算すると共に、子ノードlazyに伝播させ、自身はゼロクリアする。その後、if文①により0を㋒の段に返してノード8は終了。だから、lazy[16],lazy[17]は10となり、その後、ゼロにならずに放置される
        • ノード9は、lazy[9]がゼロではないから(以下同文)。その後、重なっているので、再帰関数として㋔(葉18,19)に移行します。
          • 葉18は、lazy[18]がゼロではないので、同マスのtreeに加算し、自身はゼロクリアする。その後、if文①により0を㋓の段に返す。
          • 葉19は、lazy[19]が(以下同文)。if文②により、同マスのtreeの値を㋓の段に返す。
          • このように、葉18,19についてはlazy配列の値が残らないこととなる。
          • ここで㋐⇒㋔に向かうセグ木の降下は終わり、次は㋔⇒㋐の戻りが実施されます。
      • ノード5経由の㋓⇒㋔への移行の説明は省略します。まぁ、ノード4経由と変わらんよ。
    • ㋔⇒㋐の戻りについては、㋔葉3,4の値 ⇒ ㋓ノード9,10 ⇒ ㋒ノード4,5 ⇒ ㋑ノード2 ⇒ ㋐ノード1 の流れで、集約され、結局、葉3(値14),葉4(値5)の合計値19がquery関数の戻り値となる。
• 以上で、「区間変更クエリ=加算クエリ、区間取得クエリ=合計クエリ」の解説は終了です。お疲れ様でした。

遅延セグ木を一般化する

• 前項は、区間変更クエリ=加算クエリ、区間取得クエリ=合計クエリという、特殊なケースのみに対応できる、使い勝手の悪い遅延セグ木になってます。
• 一方、以前作ったセグ木は、モノイドを構成する任意の二項演算と単位元を設定することが出来た。同様に、遅延セグ木でも、区間変更クエリを自由に設定したい。どのようにすれば良いだろうか？
• 結論から言うと、元々のセグ木のtree配列の中身について、モノイドを満たすことが必要だったのと同様に、新しく導入したlazy配列でも、モノイドを満たす必要がある。
• また、そして、treeとlazyのモノイドの間にモノイド射f（モノイド準同型とも呼ぶ）が存在する必要がある。
  
• 分かり易い例は以下のとおり
  • モノイドM：実数の加算＜R,+,0＞
  • モノイドM'：正の実数の乗算＜R₊,×,1＞
  • モノイド射：f(x) = $e^x$
  • 確認
    • f(x+y) = f(x) × f(z) については
      • $e^{x+y} = e^x × e^y$ 　･･･　OK!
    • f(e) = e' については
      • $e^0 = 1$　･･･　OK!
  • （蛇足）モノイド射：g(x) = ln(x) はM'⇒Mに対するモノイド射になる
    • g(x × y) = g(x) + g(y)
      • ln(xy) = ln(x) + ln(y)　･･･　OK！
    • g(e') = e
      • ln(1) = 0 ･･･　OK！
• まぁ、群環体とか、学生時代にチンプンカンプンだったので、あまり、詳細には触れないよ。とりあえず理解しておくのは、遅延セグ木の区間変更の内容も、一般化できると言うこと。
• 一般化の内容として、以下の変数（クロージャ）を設定するよ。
  • lazyの内容をtreeに作用させるモノイド射をflz
  • lazyにおける単位元lzBase
  • lazyにおける二項演算をlzOpe
• このようにした場合、以下のように書き換えられる。

import Foundation

class LazySegTree {
    private var tree: [Int]
    private var lazy: [Int]    
    private var n: Int
    private var base: Int = 0 // 合計クエリなので、0
    private var lzBase: Int = 0 // 加算クエリなので、0
    private var biOpe:(_ l:Int,_ r:Int)->Int = (+) // 合計クエリなので、(+)
    private var lzOpe:(_ u:Int,_ d:Int)->Int = (+) // 加算クエリなので、(+)
    private var flz:(_ tr:Int,_ lz:Int,_ len:Int)->Int = {$0 + $1 * $2} // 加算クエリでは、上部ノードがカバーする配列の長さ(len)に比例する。 
    
    var add:(Int,Int,Int)->() { return {self.areaOpe($0,$1,$2)} } // 区間変更クエリが加算なので、addで呼べるようにする。
    
    var top :Int {tree[1]} // treeの最上位を返す

    init(_ nums: [Int]) {
        let sz = nums.count
        n = 1
        while n < sz { n *= 2 }
        self.tree = Array(repeating: base, count: 2*n)
        self.lazy = Array(repeating: lzBase, count: 2*n)
        buildTree(nums)
    }

    convenience init(_ cnt: Int, v: Int = 0) { // 本当は、vはbaseを初期値としたい
        let nums = [Int](repeating: v, count: cnt)
        self.init(nums)
    }

    func biOpe(_ i:Int)->Int{ // 引数1つのときの関数オーバーロード
        return biOpe(tree[2*i],tree[2*i+1])
    }

    private func buildTree(_ nums: [Int]) {
        let sz = nums.count
        for i in 0..<sz {
            tree[i+n] = nums[i]
        }
        for i in stride(from: n-1, through: 1, by: -1) {
            tree[i] = biOpe(i)
        }
    }

    private func eval(_ k: Int, _ l: Int, _ r: Int) {
        if lazy[k] != 0 {
            tree[k] = flz( tree[k] , lazy[k] , r-l )
            if r - l > 1 {
                lazy[2*k] = lzOpe( lazy[k] , lazy[2*k] )
                lazy[2*k+1] = lzOpe( lazy[k] , lazy[2*k+1] )
            }
            lazy[k] = lzBase
        }
    }

    func areaOpe(_ a: Int, _ b: Int, _ x: Int, _ k: Int = 1, _ l: Int = 0, _ r: Int = -1) {
        var r = r
        if r < 0 { r = n }
        eval(k, l, r)
        if b <= l || r <= a { return }
        if a <= l && r <= b {
            lazy[k] = lzOpe( lzBase , x )
            eval(k, l, r)
        } else {
            areaOpe(a, b, x, 2*k, l, (l+r)/2)
            areaOpe(a, b, x, 2*k+1, (l+r)/2, r)
            tree[k] = biOpe(k)
        }
    }

    func query(_ a: Int, _ b: Int, _ k: Int = 1, _ l: Int = 0, _ r: Int = -1) -> Int {
        var r = r
        if r < 0 { r = n }
        eval(k, l, r)
        if b <= l || r <= a { return base }
        if a <= l && r <= b { return tree[k] }
        let vl = query(a, b, 2*k, l, (l+r)/2)
        let vr = query(a, b, 2*k+1, (l+r)/2, r)
        return biOpe(vl , vr)
    }
    func prtIndex() {
        let nums = (1..<(2*n)).map { String(format: "%2d", $0) }.joined(separator: ",")
        print("(",nums,")")
        // print(tree[1...])
    }    
    
    func prtTree() {
        let nums = tree[1...].map { String(format: "%2d", $0) }.joined(separator: ",")
        print("[",nums,"]")
        // print(tree[1...])
    }
    func prtLazyTree() {
        let nums = lazy[1...].map { String(format: "%2d", $0) }.joined(separator: ",")
        print("[",nums,"]")
        // print(lazy[1...])
    }

    func prtAry() {
        let nums = tree[n...].map { String(format: "%2d", $0) }.joined(separator: ",")
        print("[",nums,"]")    
        // print(tree[n...])
    }
}

• まぁ、見て貰えれば分かるよ。
• 上記コードを書く際、最も苦労したのは、実は、var add:(Int,Int,Int)->() { return {self.areaOpe($0,$1,$2)} }だったりします。
  • まぁ、途中から生成AIに聞いたら教えてくれたよ。細かいルールを覚えるのは、人間は不得意なんだよ。
• そう言えば、通常のセグ木に存在したupdate関数（配列要素1つだけを更新する）が抜けてたから、追加しました。

終わりに

• この遅延セグ木は難敵だったよ。
• 国内で、swiftでの解説をした人はいないんじゃないかな？
• このLazySegTreeをつかって、swiftでコンテストを戦う仲間が増えたら嬉しい。

おまけ（「区間加算」「区間最大値」の場合）

• 一般化した遅延セグ木を「区間加算」「区間最大値」としたコードを載せます。

import Foundation

class LazySegTree {
    var tree: [Int]
    var lazy: [Int]    
    var n: Int
    private var base: Int = -99 // maxクエリなので、負の大きい数
    private var lzBase: Int = 0 // 加算クエリなので、0
    private var biOpe:(_ l:Int,_ r:Int)->Int = max // maxクエリなので、max
    private var lzOpe:(_ u:Int,_ d:Int)->Int = (+) // 加算クエリなので、(+)
    private var flz:(_ tr:Int,_ lz:Int,_ len:Int)->Int = {($0 == -99 ? 0 : $0) + $1 + $2 * 0} // 加算クエリでは、上部ノードがカバーする配列の長さ(len)に比例する。 
    
    // 区間変更クエリが加算の時の便利な省力化関数
    var add:(Int,Int,Int)->() { return {self.areaOpe($0,$1,$2)} } // 区間変更クエリが加算なので、add(a,b,x)（範囲a..<bにxを加算）で呼べるようにする。
    var update:(Int,Int)->() {
        return {
            self.areaOpe($0,$0+1,$1 - (self.query($0,$0+1) == self.base ? 0 : self.query($0,$0+1)))// add(i,i+1,x-query(i,i+1))と書くのが面倒なので、update関数を作成
        }
    }
    
    init(_ nums: [Int]) {
        let sz = nums.count
        n = 1
        while n < sz { n *= 2 }
        self.tree = Array(repeating: base, count: 2*n)
        self.lazy = Array(repeating: lzBase, count: 2*n)
        buildTree(nums)
    }

    convenience init(_ cnt: Int, v: Int = -99) { // 本当は、vはbaseを初期値としたい
        let nums = [Int](repeating: v, count: cnt)
        self.init(nums)
    }

    func biOpe(_ i:Int)->Int{ // 引数1つのときの関数オーバーロード
        return biOpe(tree[2*i],tree[2*i+1])
    }

    private func buildTree(_ nums: [Int]) {
        let sz = nums.count
        for i in 0..<sz {
            tree[i+n] = nums[i]
        }
        for i in stride(from: n-1, through: 1, by: -1) {
            tree[i] = biOpe(i)
        }
    }

    private func eval(_ k: Int, _ l: Int, _ r: Int) {
        if lazy[k] != 0 {
            tree[k] = flz( tree[k] , lazy[k] , r-l )
            if r - l > 1 {
                lazy[2*k] = lzOpe( lazy[k] , lazy[2*k] )
                lazy[2*k+1] = lzOpe( lazy[k] , lazy[2*k+1] )
            }
            lazy[k] = lzBase
        }
    }

    func areaOpe(_ a: Int, _ b: Int, _ x: Int, _ k: Int = 1, _ l: Int = 0, _ r: Int = -1) {
        var r = r
        if r < 0 { r = n }
        eval(k, l, r)
        if b <= l || r <= a { return }
        if a <= l && r <= b {
            lazy[k] = lzOpe( lzBase , x )
            eval(k, l, r)
        } else {
            areaOpe(a, b, x, 2*k, l, (l+r)/2)
            areaOpe(a, b, x, 2*k+1, (l+r)/2, r)
            tree[k] = biOpe(k)
        }
    }

    func query(_ a: Int, _ b: Int, _ k: Int = 1, _ l: Int = 0, _ r: Int = -1) -> Int {
        var r = r
        if r < 0 { r = n }
        eval(k, l, r)
        if b <= l || r <= a { return base }
        if a <= l && r <= b { return tree[k] }
        let vl = query(a, b, 2*k, l, (l+r)/2)
        let vr = query(a, b, 2*k+1, (l+r)/2, r)
        return biOpe(vl,vr)
    }
    
    func prtIndex() {
        let nums = (1..<(2*n)).map { String(format: "%3d", $0) }.joined(separator: ",")
        print("(",nums,")")
    }    
    
    func prtTree() {
        let nums = tree[1...].map { String(format: "%3d", $0) }.joined(separator: ",")
        print("[",nums,"]")
        // print(tree[1...])
    }
    func prtLazyTree() {
        let nums = lazy[1...].map { String(format: "%3d", $0) }.joined(separator: ",")
        print("[",nums,"]")
        // print(lazy[1...])
    }

    func prtAry() {
        let nums = tree[n...].map { String(format: "%3d", $0) }.joined(separator: ",")
        print("[",nums,"]")    
        // print(tree[n...])
    }

}

• 上記を下記で実行しました。ちなみに、上記は見やすさの観点から、max関数の単位元を「-99」としました。

// 初期配列の定義
let initialArray = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
let segTree = LazySegTree(initialArray)

// 説明
let str = """
1行目：セグ木のインデックス(1スタート)
2行目：セグ木の要素(tree)
3行目：セグ木の遅延要素(lazy)
4行目：評価対象配列の要素(tree[n...]、0-idxだから1行目のインデックスとは1ズレる)

""" 
print(str)


// 初期状態のセグメント木を表示
print("初期状態のセグメント木:")
segTree.prtIndex()
segTree.prtTree()
segTree.prtLazyTree()
segTree.prtAry()

// 区間取得クエリ 1..<5 の最大値
let initialMax = segTree.query(1, 5)
print("区間 [1, 5) の初期最大値: \(initialMax)\n")

// 区間加算クエリ 0..<4の範囲で10を加算
print("区間加算クエリ 0..<4の範囲で10を加算")
segTree.add(0,4,10)

// 加算後のセグメント木を表示（遅延評価前）
print("加算後、遅延評価前のセグメント木:")
segTree.prtIndex()
segTree.prtTree()
segTree.prtLazyTree()
segTree.prtAry()
print()

// 加算後のセグメント木の最大値
let addedMax = segTree.query(3,5)
print("区間 [3, 5) の加算後最大値: \(addedMax)")

// 加算後のセグメント木を表示（遅延評価後）
print("区間 [3, 5) の取得クエリ後のセグメント木:")
segTree.prtIndex()
segTree.prtTree()
segTree.prtLazyTree()
segTree.prtAry()
print()

// 加算後の値アップデート
let newVal = 11
segTree.update(3,newVal)
print("インデックス[3] の値更新: \(newVal)")

// 加算後のセグメント木を表示（遅延評価後）
print("インデックス[3] の値更新後のセグメント木:")
segTree.prtIndex()
segTree.prtTree()
segTree.prtLazyTree()
segTree.prtAry()
print()
// アップデート後のセグメント木の最大値
let updatedMax = segTree.query(3,5)
print("区間 [3, 5) の加算後最大値: \(updatedMax)")

• 結果は以下のとおり

1行目：セグ木のインデックス(1スタート)
2行目：セグ木の要素(tree)
3行目：セグ木の遅延要素(lazy)
4行目：評価対象配列の要素(tree[n...]、0-idxだから1行目のインデックスとは1ズレる)

初期状態のセグメント木:
(   1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 )
[  10,  8, 10,  4,  8, 10,-99,  2,  4,  6,  8, 10,-99,-99,-99,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10,-99,-99,-99,-99,-99,-99 ]
[   0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0 ]
[   1,  2,  3,  4,  5,  6,  7,  8,  9, 10,-99,-99,-99,-99,-99,-99 ]
区間 [1, 5) の初期最大値: 5

区間加算クエリ 0..<4の範囲で10を加算
加算後、遅延評価前のセグメント木:
(   1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 )
[  14, 14, 10, 14,  8, 10,-99,  2,  4,  6,  8, 10,-99,-99,-99,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10,-99,-99,-99,-99,-99,-99 ]
[   0,  0,  0,  0,  0,  0,  0, 10, 10,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0 ]
[   1,  2,  3,  4,  5,  6,  7,  8,  9, 10,-99,-99,-99,-99,-99,-99 ]

区間 [3, 5) の加算後最大値: 14
区間 [3, 5) の取得クエリ後のセグメント木:
(   1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 )
[  14, 14, 10, 14,  8, 10,-99, 12, 14,  6,  8, 10,-99,-99,-99,  1,  2, 13, 14,  5,  6,  7,  8,  9, 10,-99,-99,-99,-99,-99,-99 ]
[   0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0, 10, 10,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0 ]
[   1,  2, 13, 14,  5,  6,  7,  8,  9, 10,-99,-99,-99,-99,-99,-99 ]

インデックス[3] の値更新: 11
インデックス[3] の値更新後のセグメント木:
(   1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 )
[  13, 13, 10, 13,  8, 10,-99, 12, 13,  6,  8, 10,-99,-99,-99,  1,  2, 13, 11,  5,  6,  7,  8,  9, 10,-99,-99,-99,-99,-99,-99 ]
[   0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0, 10, 10,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0 ]
[   1,  2, 13, 11,  5,  6,  7,  8,  9, 10,-99,-99,-99,-99,-99,-99 ]

区間 [3, 5) の加算後最大値: 11