- 実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門を読んだので、復習も兼ねて第1部のメモ
- RとStanではじめる ベイズ統計モデリングによるデータ分析入門:サポートページ
- 読んだときに作ったR、Stanのファイルはココ
何が書いてある本か
- 第1部:ベイズ統計モデリングによるデータ分析の方法。(このページ)
- 第2部~:RとStanを用いて実際にサンプルデータの可視化、分析、推定結果の図示を行う方法(後日、別でまとめたい)
ベイズ統計モデリング
統計モデル・ベイズ推論によってデータを分析する手法。また、この本ではモデルや事後確率分布の評価にMCMC(マルコフ連鎖モンテカルロ法、Markov chain Monte Carlo methods)を用いている
統計モデル
- 統計モデル:データに適合するように構築された確率モデル
- 確率モデル:確率的な表現が用いられた数理モデル
- 数理モデル:数式を用いて表現されたモデル
- モデル:観測したデータを生み出す確率的な過程を簡潔に記述したもの
- モデリング:モデルを作る行為。
確率モデルで使われる確率分布
他にもいろいろあるが、代表的なもの
- 離散型:離散一様分布、ベルヌーイ分布、二項分布、ポアソン分布
- 連続型:連続一様分布、正規分布、対数正規分布、t分布
統計モデルの例
$f(Y)$は、$Y$が出る確率
- 二項分布:コインの表が出る確率を$p$として、10回投げて$Y$回表が出る
Y \sim Binom(10, p) \\
f(Y|N, p) = _{10}C_Y p^Y (1-p)^{N-Y}
- 正規分布:平均$\mu$、標準偏差$\sigma$に従う商品の売上高$Y$
Y \sim Normal(\mu, \sigma^2) \\
f(Y) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp(- \frac {(y-\mu)^2}{2 \sigma^2})
- 正規分布:平均$\mu$が気温$x$によって変わり、標準偏差$\sigma$に従う商品の売上高$Y$
\mu = \beta_0 + \beta_1 x \\
Y \sim Normal(\mu, \sigma^2) \\
f(Y) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp(- \frac {(y-\mu)^2}{2 \sigma^2})
ベイズ推論
ベイズの定理を用いたベイズ更新によって、興味の対象となる条件付き確率を得ること
ベイズの定理
$A$が発生する確率を$P(A)$、$X$が発生したという条件で$A$が発生する確率を$P(A|X)$とすると
P(X|A) = \frac {P(A|X) P(X)} {P(A)}
$P(A) \neq 0$の条件で以下の式を変形した、と考えるとわかりやすい。(両辺とも$A$と$X$が同時に発生する確率)
P(X|A) P(A) = P(A|X) P(X)
ベイズ更新
ベイズの定理の$A$を$D$にして少し書き方を変えると
P(X|D) = \frac {P(D|X)} {P(D)} P(X)
となる。このとき、$X$を確率分布のパラメータ(統計モデルの$p$とか$\mu$とか$\sigma$)、$D$を実際に得られたデータとすると、この式の意味は
「事前確率(何もデータがないときのパラメータ$X$の確率)に、データ$D$の情報を使うと、事後確率(データ$D$が得られたという条件でのパラメータ$X$の確率)に更新される」
という意味になる。
例題(モンティ・ホール問題)
- A, B, Cのドアのうち1つが正解の場合、事前確率は$P(A) = P(B) = P(C) = \frac{1}{3}$
- 回答者がドアAを選び、出題者がドアCを開けて「ドアCは正解ではない」と示す(この情報をDとする)
- このとき、$P(D), P(D|A), P(D|B), P(D|C)$は「回答者がドアAを選ぶ確率×出題者がドアCを開ける確率」なので以下のようになる。(出題者は正解を知ってるので、回答者が選んだドアと正解のドアを避けて開く)
P(D) = \frac{1}{3} \frac{1}{2} = \frac{1}{6} \\
P(D|A) = \frac{1}{3} \frac{1}{2} = \frac{1}{6} \\
P(D|B) = \frac{1}{3} 1 = \frac{1}{3} \\
P(D|C) = \frac{1}{3} 0 = 0 \\
- これらを使ってベイズ更新すると、$P(A|D), P(B|D), P(C|D)$は以下になる
P(A|D) = \frac {P(D|A)} {P(D)} P(A) = \frac {\frac{1}{6}} {\frac{1}{6}} \frac{1}{3} = \frac{1}{3} \\
P(B|D) = \frac {P(D|B)} {P(D)} P(B) = \frac {\frac{1}{3}} {\frac{1}{6}} \frac{1}{3} = \frac{2}{3} \\
P(C|D) = \frac {P(D|C)} {P(D)} P(C) = \frac {0} {\frac{1}{6}} \frac{1}{3} = 0 \\
ベイズ統計の解説動画
ベイズ統計については、この動画がわかり易かった
AIcia Solid Project - ベイズ統計
MCMC(マルコフ連鎖モンテカルロ)法
- MCMC(Markov chain Monte Carlo methods)法:マルコフ連鎖を利用して乱数を生成する手法。
- 上の例題では簡単に事後確率を求められたが、実際には求めるのに複雑な計算が必要な場合が多い。(特に、パラメータやデータが連続型だと複雑な積分計算が必要)
- そのため、頑張って全部は計算しないで、MCMCで事後確率分布に従う乱数を生成して、その乱数の平均値などを使う
モンテカルロ法
- モンテカルロ法(Monte Carlo method):シミュレーションや数値計算を乱数を用いて行う手法の総称
- 今回は、積分計算を乱数を使って代替する(モンテカルロ積分)
例
求めたいパラメータ$\theta$があり、データ$D$が得られたときの事後確率分布を$f(\theta|D)$とすると、$\theta$の期待値は以下になる。(「$\theta$が発生する確率と$\theta$をかけあわせたもの」を全パターン足したもの)
\int_{-\infty}^{\infty}f(\theta|D)d\theta
このとき$f(\theta|D)$が複雑すぎると積分計算できない。
ここで、かわりに事後分布に従う乱数$\hat{\theta}$を1000個($\hat{\theta}_1, \hat{\theta}_2, ..., \hat{\theta} _{1000}$)発生できたとすると、期待値は以下のようになる。
\frac{\sum_{i=1}^{1000} \hat{\theta_i}}{1000}
厳密な答えとは多少ズレるが、乱数の数を十分に大きくすれば実用的には問題ない近い値になる。
マルコフ連鎖
- あるステップでの状態が、その直前の状態のみに依存するモデル(2ステップ以上前には依存しない)
- 例:今日の天気は、昨日の天気によって決まる。(一昨日の天気は関係ない)
例題
以下の場合、全体でどのくらい晴れ・曇り・雨になるのかを求める
- 今日が晴れだったら、次の日は晴れ70%、曇り20%、雨10%
- 今日が曇りだったら、次の日は晴れ30%、曇り50%、雨20%
- 今日が雨だったら、次の日は晴れ20%、曇り40%、雨40%
[パターン1]
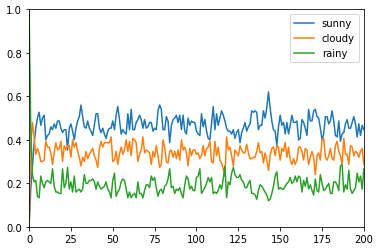
- 150個の場所でスタート時点ですべて雨として、200回更新する
- 晴れ、曇り、雨のどれも、ある程度の確率で安定している
[パターン2]
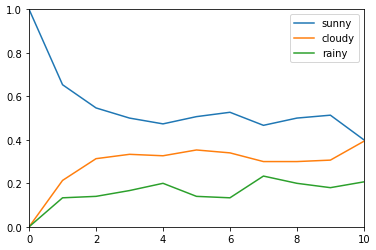
- 150個の場所でスタート時点ですべて晴れとして、10回更新する
- コレだと、収束してるのかどうかわからない = 回数が少なすぎると収束しない
# ライブラリ読み込み&初期設定
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
%matplotlib inline
# 初期の配分
scr_cnt = {
's': 150,
'c': 0,
'r': 0,
}
# 繰り返し回数
iter_num = 10
# 乱数設定
seed = 0
# 天気更新用の関数
# 晴れs:0、くもりc:1、雨r:2
def update_w(w):
rand = random.random()
# 移行確率
ratio = {
0: {0: 0.7, 1: 0.2, 2: 0.1}, # 晴れ - >晴れ、くもり、雨
1: {0: 0.3, 1: 0.5, 2: 0.2}, # くもり-> 晴れ、くもり、雨
2: {0: 0.2, 1: 0.4, 2: 0.4}, # 雨- > 晴れ、くもり、雨
}
r_cum = 0
for i, r in ratio[w].items():
r_cum += r
if rand < r_cum:
return i
# 乱数を生成
# 初期状態
w = np.concatenate((np.repeat(0, scr_cnt['s']),
np.repeat(1, scr_cnt['c']),
np.repeat(2, scr_cnt['r'])),
axis=0)
# 結果格納用
x = []
s_ratios = []
c_ratios = []
r_ratios = []
# 初期値格納
s_ratio = sum(x==0 for x in w) / len(w)
c_ratio = sum(x==1 for x in w) / len(w)
r_ratio = sum(x==2 for x in w) / len(w)
x.append(0)
s_ratios.append(s_ratio)
c_ratios.append(c_ratio)
r_ratios.append(r_ratio)
random.seed(seed)
for i in range(iter_num):
w = list(map(update_w, w)) # 天気更新
s_ratio = sum(x==0 for x in w) / len(w)
c_ratio = sum(x==1 for x in w) / len(w)
r_ratio = sum(x==2 for x in w) / len(w)
x.append(i+1)
s_ratios.append(s_ratio)
c_ratios.append(c_ratio)
r_ratios.append(r_ratio)
# プロット
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, s_ratios, label='sunny')
ax.plot(x, c_ratios, label='cloudy')
ax.plot(x, r_ratios, label='rainy')
ax.set_xlim([0, iter_num])
ax.set_ylim([0, 1])
ax.legend(loc='best')
plt.show()
# 乱数の統計量を算出
df_ratios = pd.DataFrame({
'sunny': s_ratios,
'cloudy': c_ratios,
'rainy': r_ratios,
})
# 初期値の影響を受けやすい値(今回は前半の半分)を除外
df_ratios.loc[len(df_ratios)//2:, :].describe()
事後分布に従う乱数の生成
- この本では「メトロポリス・ヘイスティングス法(MH法)」と「ハミルトニアンモンテカルロ法(HMC法)」について書かれている
- ここにはMH法のみ書く(HMC法は、都度ググる)
メトロポリス・ヘイスティングス法(MH法)
- データ$D$が得られたとする
- データが生成されるモデル(確率分布)を考え、適当にパラメータの初期値$\hat{\theta}_1$を決める
- $\hat{\theta_1}$に適当な乱数(正規分布で生成する)を足して、$\hat{\theta_2}^{仮}$とする
- データ$D$が得られた状態での事後確率$f(\hat{\theta_1}|D), f(\hat{\theta_2}^{仮}|D)$を比べ、決められたルールに従い$\hat{\theta_2}$を決定する
- 同様に、$i=3, 4, \cdots$についても$\hat{\theta_i}$を求めていく
- 一定数$\hat{\theta}$が得られたら、初期値の影響を受ける最初の方の$\hat{\theta}$を除外し、残った$\hat{\theta}$の平均値などをとってパラメータの点推定値とする
$\hat{\theta_i}$の決定方法
ベイズの定理より
f(\theta|D) = \frac {f(D|\theta) f(\theta)} {f(D)}
なので、$\hat{\theta_2}^{仮}, \hat{\theta_1}$の事後確率を比較した$rate$は、$f(D|\theta) f(\theta) = Kernel(\theta)$とおくと
\begin{align}
rate &= \frac {f(\hat{\theta_2}^{仮}|D)}{f(\hat{\theta_1}|D)} \\
&= \frac {f(D|\hat{\theta_2}^{仮}) f(\hat{\theta_2}^{仮})} {f(D)} \frac {f(D)} {f(D|\hat{\theta_1}) f(\hat{\theta_1})} \\
&= \frac {f(D|\hat{\theta_2}^{仮}) f(\hat{\theta_2}^{仮})} {f(D|\hat{\theta_1}) f(\hat{\theta_1})} \\
&= \frac {Kernel(\hat{\theta_2}^{仮})} {Kernel(\hat{\theta_1})} \\
\end{align}
- rateが1を超えると、$\hat{\theta_2}^{仮}$のほうが事後確率が高い
- 計算するのが難しい$f(D)$が消えており、計算可能となっている
$rate$を求めた後は、以下のように$\hat{\theta_i}$を更新する
- $rate > 1$の場合:$\hat{\theta_i} = \hat{\theta_i}^{仮}$とする
- $rate < 1$の場合:確率$rate$で$\hat{\theta_i} = \hat{\theta_i}^{仮}$、確率$(1-rate)$で$\hat{\theta_i} = \hat{\theta_{i-1}}$とする
「変更したほうが事後確率が上がる場合、確定で変更」「変更したほうが事後確率が下がる場合も、変更することもある」
得られた乱数の取り扱いの注意
- 各種設定:chains、iter、warmup、thin
- 収束の評価
- 代表値のとり方:事後中央値、事後期待値(平均)、事後確率最大値(最頻値)