ハミルトニアンモンテカルロ法

はじめに

「ハミルトニアンモンテカルロ法」は、モデルのパラメータを推定する手法であり、
マルコフ連鎖モンテカルロ法（MCMC法）の一種である。
確率的プログラミング言語のStanやPyMCで実装されており、誰でも容易に使うことができる。

様々なパラメータの推定手法

このようなモデルのパラメータを推定する方法に、「EMアルゴリズム」がある。
EMアルゴリズムは、Jensenの不等式を用いて、周辺化対数尤度を下限で近似する。

$
log\ p(x{\mid}{\theta}) \geq E_{z {\sim} q(z)} [log\ p(x, z {\mid}\theta)]
$

そして、右辺を最大化することで、左辺の周辺化対数尤度に近づけていく。

しかし、モデル$p(x, z {\mid}\theta)$ が複雑だと、それ自体の解析的な計算ができないため、
EMアルゴリズムを適用することができない。

そのような、複雑なモデルのパラメータを推定する方法として、
「変分ベイズ法」や「ギブスサンプリング法」、
そして、今回説明する「ハミルトニアンモンテカルロ法」を含むMCMC法がある。

MCMCサンプルの使い道

事後確率に従うサンプルを得る方法としてMH法がある。
これは、尤度、事前確率それぞれのカーネルが分かれば用いることができる。

ここでのカーネルとは、正規化項を除いた確率分布の形状を表す関数のことである。
例えば、ガウス分布であれば、指数の部分がカーネルに相当する。

サンプルが得られれば、任意の関数$g(\theta)$の確率的平均を近似計算できる。
例えば、パラメータがある値以上を取る確率などを求めることができる。

$
{\int} g(\theta) p({\theta} {\mid} x) d{\theta}
= E_{{\theta} {\sim} p({\theta} {\mid} x)}[g(\theta)]
\approx \sum _i g(\theta _i)
$

このような事後確率からのサンプルを得るには、遷移核が詳細釣り合い条件を満たす必要がある。
遷移核とは、パラメータ空間において現在位置から、次にどこへ遷移するかを決める確率である。

サンプルが平均$\mu=170$のガウス分布に従うような、平均身長の例だと、
仮に$168$にいたときに、$167$に遷移する確率、$169$に遷移する確率などを束ねたものである。

メトロポリスヘイスティング法の課題

しかしながら、MH法は遷移核の候補分布を適切に選ばなければ上手く機能しない。
具体的には、以下のような点が挙げられる。

1. 受容率が低く、事後確率に従うサンプルを十分に得られない
2. 前後のサンプルの相関が高く、パラメータ空間を網羅できない

パラメータ数が少ない低次元空間であれば遷移核の分布は割と簡単に決めれるが、
数十以上のパラメータの高次元空間だと、事後分布の形状自体を目視で確認できない。

そこで、上記の課題を解決するのがハミルトニアンモンテカルロ法である。

ハミルトニアンについて

力学について簡単に復習をする。厳密性は除く。
ハミルトニアンは物体のもつ力学的エネルギーを、位相空間で表現したものである。
位相空間とは、運動量と位置で張られる空間のことである。

$
ハミルトニアン = 力学エネルギー + 位置エネルギー
$

エネルギー保存の法則より、ハミルトニアンは時間に関わらず一定である。

坂を転げ落ちる物体の例

坂を転げ落ちる物体を例にとる。ここでは、物体は大きさを持たない質点とする。
物体は、坂を下るにつれて加速し、最下点で運動エネルギーは$K$は最大になる。
一方で、位置エネルギー$U$は最下点において最小になる。

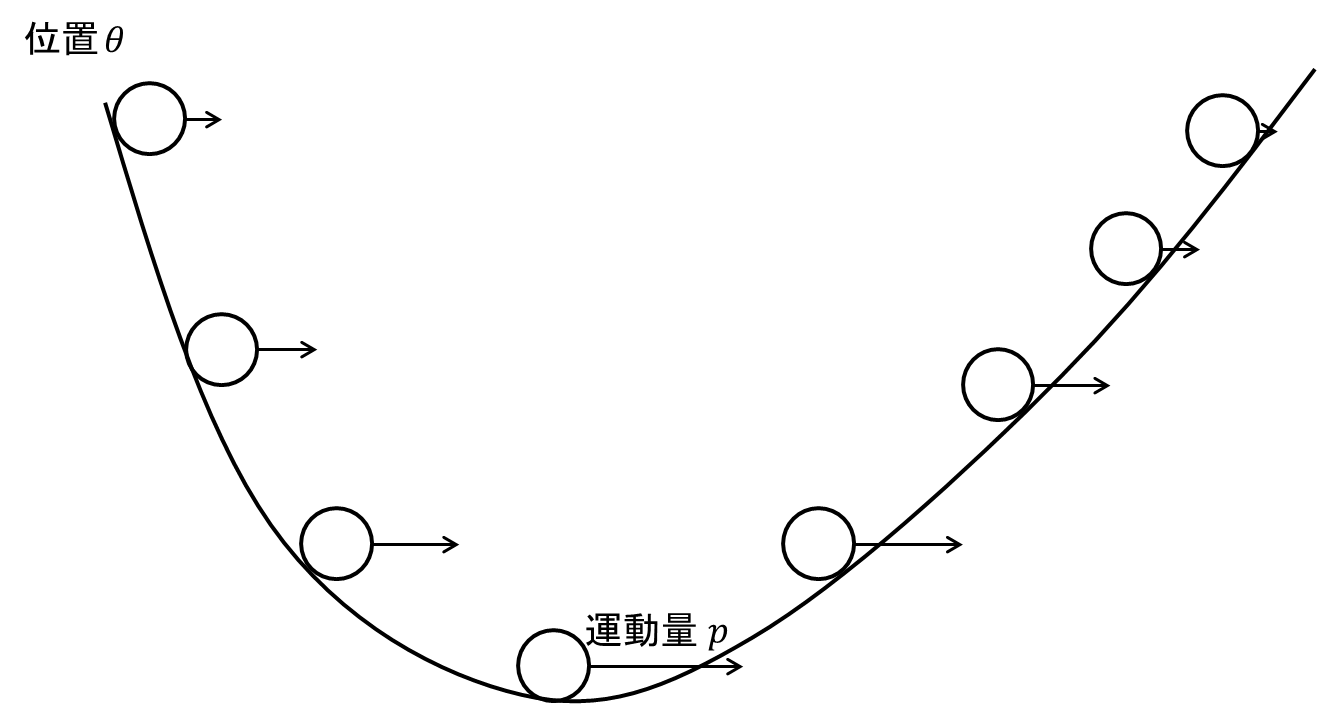
逆に坂を上るにつれて減速し、最上点で運動エネルギーは$K$は最小になり、
位置エネルギー$U$は最上点において最大になる。

速度と加速度

速度$v(t)$および、加速度$a(t)$は以下の式で表され、位置$\theta(t)$の関数となっている。

$
v(t) = \frac {d\theta(t)} {dt}
$

$
a(t) = \frac {dv(t)} {dt}
= \frac {d^2\theta(t)} {dt^2}
$

速度$v(t)$は、微小時間における位置$\theta(t)$の変化量である。
加速度$a(t)$は、微小時間における速度$v(t)$の変化量である。

#運動エネルギーと位置エネルギー

運動エネルギーは以下で表される。運動量 $p(t) = mv(t)$を用いて変形を行った。

$
K(t) = \frac {1} {2} mv(t)^2 = \frac {p(t)^2} {2m}
$

また、位置エネルギー$U(t)$は以下で表される。$g$は重力加速度を表す。

$
U(t) = mgh(t)
$

ハミルトニアンとエネルギー保存則

ハミルトニアン$H(t)$は以下のように表され常に一定である。

$
H(t) = K(t) + U(t)
= \frac {p(t)^2} {2m} + mgh(t)
$

ここでは、位置$\theta(t)$によって、高さ$h(t)$が定まるとする。

また、物体の質量を$m=1$、重力加速度を$g=1$とすると、
ハミルトニアンは以下のように表される。

$
H(t) = \frac {1} {2} p(t)^2 + h(\theta(t))
$

ハミルトニアンと位相空間

位置$\theta(t)$と、運動量$p(t)$で表された空間を位相空間と呼ぶ。
物体はハミルトニアンが一定となるように動き、位相空間で等高線を描く。
以下の図において破線の一周が、上記の例で物体が行って戻って来るまでを表す。

ハミルトンの運動方程式

物体の運動は以下の微分方程式によって定められる。

$
a(t) = \frac {dp(t)} {dt} = - \frac {dU({\theta}(t))} {d{\theta}(t)}
$

$
v(t) = \frac {d{\theta}(t)} {dt} = \frac {dK(p(t))} {dp(t)}
$

上式はハミルトニアンが一定であることから導ける。ここでは$m=1$と置いている。

$
\frac {dH(t)} {dt} = 0 \
\leftrightarrow　\frac {dK(t)} {dt} = - \frac {dU(t)} {dt}\
\leftrightarrow　\frac {dK(p(t))} {dp(t)} \frac {dp(t)} {dt} = - \frac {dU({\theta}(t))} {d{\theta}(t)} \frac {d{\theta}(t)} {dt}
$

運動量の数値演算による近似

運動量の微小変化を漸化式として近似し、次の時刻の運動量を求める。

$
\frac {dp(t)} {dt} = - \frac {dU({\theta}(t))} {d{\theta}(t)}\
\leftrightarrow　\frac {p(t+1) - p(t)} {dt} = - h^{\prime} ({\theta}(t))\
\leftrightarrow　p(t+1) = p(t) - h^{\prime} ({\theta}(t)) dt\
$

位置の数値演算による近似

位置の微小変化を漸化式として近似し、次の時刻の位置を求める。

$
\frac {d{\theta}(t)} {dt} = - \frac {dK(p(t))} {dp(t)}\
\leftrightarrow　\frac {{\theta}(t+1) - {\theta}(t)} {dt} = \frac {d} {dp(t)} \frac {1} {2} p(t)^2 = p(t)\
\leftrightarrow　{\theta}(t+1) = {\theta}(t) + p(t) dt\
$

しかしながら、この前進差分による近似は演算誤差が大きい。

リープフロッグ法を用いた高精度な近似

運動量$p$の変化量を$\frac{1}{2}$ステップにして、位置${\theta}$を高精度に得る。
最終的に、位置${\theta}$を得たいパラメータのサンプルと見立てることを考えている。

$
p(t+\frac{1}{2}) = p(t) - h^{\prime} ({\theta}(t)) \frac{1}{2}dt
$

$
{\theta}(t+1) = {\theta}(t) + p(t+\frac{1}{2}) dt
$

このあと、位置エネルギーを事後確率として読みかえる。

詳細釣り合い条件：パラメータの事後確率

同じハミルトニアン上での異なる点の事後確率は同じである。

$
f({\theta}, p {\mid} x) = f({\theta}^{\prime}, p^{\prime} {\mid} x)
$

詳細釣り合い条件：パラメータの遷移核

物体をはじき運動量を与えることを考えると横軸$p$上で物体が遷移する。
遷移先のハミルトニアンは運動量$p$によって決まる。

低いところからは大きな運動量が必要で、逆は小さな運動量で済む。

$
f({\theta}, p {\mid} {\theta}^{\prime}, p^{\prime}) = f({\theta}^{\prime}, p^{\prime} {\mid} {\theta}, p)
$

物体に与える運動量とハミルトニアンの関係

物体をはじくための運動量は標準正規分布でランダムに決定する。
そのため、事後確率において運動量$p$と位置$\theta$は独立である。

$
f(p) = N(p {\mid} 0, 1) \propto exp(- \frac{1}{2} p^2)
$

$
f({\theta}, p {\mid} x) = f(\theta {\mid} x) f(p)
$

これより、先ほど考えていた事後確率はハミルトニアンと一致する。

$
f({\theta}, p {\mid} x) = exp(log f(\theta {\mid} x) + log f(p))\
\propto exp(- h(\theta {\mid} x) - \frac{1}{2} p^2)
= exp(- H(\theta, p))
$

ただし、$h(\theta {\mid} x) = - log f(\theta {\mid} x)$のように事後確率を高さと置いている。

ハミルトニアンモンテカルロ法

以上より、詳細釣り合い条件は次のようになる。
$
{f({\theta}^{\prime}, p^{\prime} {\mid} {\theta}, p) f({\theta}, p {\mid} x)} =
{f({\theta}, p {\mid} {\theta}^{\prime}, p^{\prime}) f({\theta}^{\prime}, p^{\prime} {\mid} x)}
$

よって、HMC法におけるサンプルの棄却率$r$は、次のように定められる。

$
r = \frac {f({\theta}^{\prime}, p^{\prime} {\mid} {\theta}, p) f({\theta}, p {\mid} x)}
{f({\theta}, p {\mid} {\theta}^{\prime}, p^{\prime}) f({\theta}^{\prime}, p^{\prime} {\mid} x)}
= \frac {f({\theta}, p {\mid} x)}
{f({\theta}^{\prime}, p^{\prime} {\mid} x)}\
= \frac {exp(- H(\theta, p))} {exp(- H({\theta}^\prime, p^\prime))}
= exp(H({\theta}^\prime, p^\prime) - H(\theta, p))
$

$0から1$の間でランダムに選んできた数値より、$r$が高ければ受容する。
上式は理論的には$r=1$となり、必ず受容するはずである。

しかし、物体の遷移はリープフロッグ法で計算しているため演算誤差が生じる。
そのため、わずかに棄却されるが、ほぼ正しいサンプルとして受容される。

HMC法を用いた正規分布の推定

身長が平均$170cm$、標準偏差が${\pm}7cm$の100人のデータ$x$がある。
HMC法で1万サンプルを取得して正規分布のパラメータ$\mu$と$\sigma$を推定する。
今回は、事前確率を一様分布と適当において計算する。

$\mu_{MAP}$	$\sigma_{MAP}$	$std(\mu_{MAP})$	$std(\sigma_{MAP})$
168.9	6.98	0.71	2.74

結果、受容率が$100％$で真値とほぼ正しい結果が得られている。
また、パラメータの事後標準偏差が得られており、特性が読み取れる。

おわりに

ハミルトニアンモンテカルロ法により、より少ない計算量でパラメータを得ることができる。
確率的プログラミング言語のStanやPyMCで試すことができるので、
自分でモデルを作り実際の効果を確認してみるとよいだろう。

今回の記事をまとめたスライドを以下にあげておいた。

https://www.slideshare.net/ssuserc768a6/ss-77659007

参考文献

豊田秀樹. 基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門. 朝倉書店, 2015.