概要
- 本でStanを使った状態空間モデルによる分析方法を勉強したから、実際のデータで練習してみたもの
- 目標は「イベント開始日の時点で、イベント終了時の1位のポイントを推定する」
- 1位を取ったから何か報酬があるわけでもないので、実用性は無い
- 今回使ったのは、状態空間モデルの「ローカル線形トレンド」+「時系変数」モデル
-
結果としては、十分な精度をもったモデルが作れたと思われる
- 1位は「トレンド」「イベント期間の長さ」で、ほぼ説明しきれた
- やはり、2001位の予想よりは簡単だった
- 1位には「イベントごとの盛り上がり具合」はあまり影響せず、ガチ勢が最高効率で時間いっぱい走るためと思われる
- 今回作ったスクリプトたちの置き場所はココ。
- 2001位の予想が難しく、説明変数を検討中のため、気分転換も兼ねてやってみたもの
使うデータ
ココで取得したデータを、形式がアタポンのものだけ抽出したもの
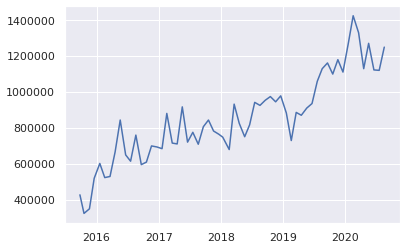
- 1位ポイント(目的変数)
- イベント期間の長さ(h)(説明変数)
「ローカル線形トレンド」+「時系変数」モデル
- ローカル線形トレンドモデルや時系変数モデルの中身の数式とかはコッチ参照
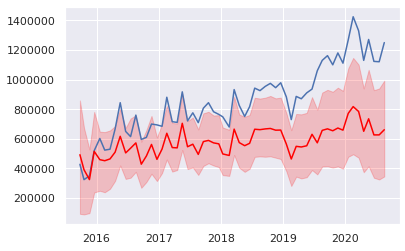
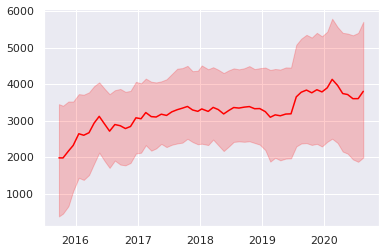
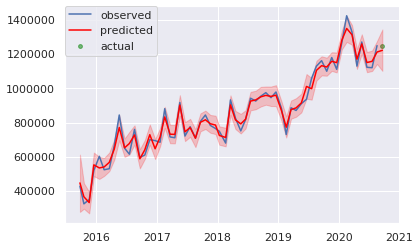
- 赤線が点推定で、赤い範囲が区間推定(5%-95%区間)
- モデル作成に使ったデータに対する、区間推定の正解率は91.7%(全数: 60、正解数: 55)
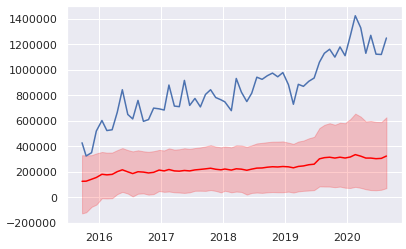
トレンド成分(A)
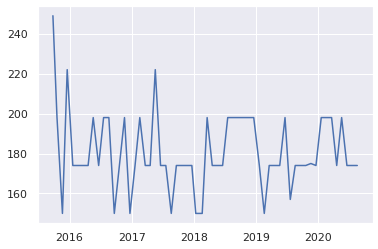
「イベント期間の長さ」による成分(B)
- 時系変数の係数
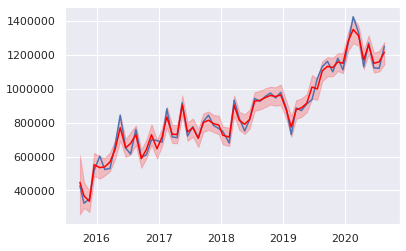
予測モデル(A+B)
- トレンド成分と係数を比較すると、「トレンドは滑らか」「係数は急に変化する」傾向がある
- 「性能の高いキャラの追加」「グランドライブの実装」などの時間効率に影響する要因が、係数に乗ったと思われる
実測と予測の比を見てみる
- 「比 = 実測値 / 予測値」として、比を見てみる
- 「値が大きかったら、ズレも大きくなりがちだよね」という考え
- 「比=1」でピタリ賞
- 1以上で予測値 < 実測値。1以下で実測値 < 予測値
統計量
- 平均は約1(そこを狙ってモデル作られているので、コレは当たり前)
- 標準偏差0.043 = 正規分布の場合、68%は±4.3%に入る
- 最大のズレは約13%(min, max)
- 50%はズレ3.3%未満(25%-75%)
| ズレ | |
|---|---|
| count | 60 |
| mean | 0.9977 |
| std | 0.0439 |
| min | 0.8816 |
| 25% | 0.9679 |
| 50% | 1.0000 |
| 75% | 1.0199 |
| max | 1.1269 |
プロット
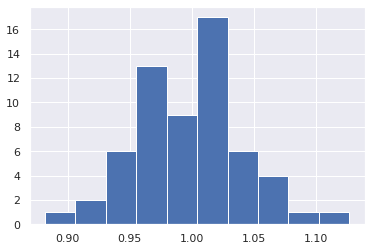
- ヒストグラム
- 正規分布に近い
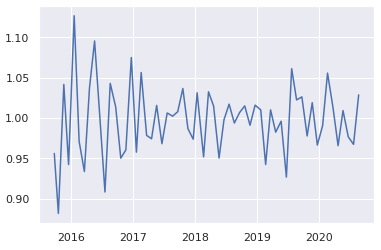
- 時系列
他にも大きい順に見てみたり、月別で見てみたりしたが、あまり規則性は見られなかった。
実際のイベント1位を推定する
-
↑のモデル作成には、イベント一覧のヒーローヴァーサスレイナンジョー以前のデータを使ったため、その次に開催されたオレンジタイムの1位ポイントを推定してみた
-
「オレンジタイム」の情報
- 開催日:2020/09/20
- 期間:174h
- 1位ポイント(答え):1,250,000
-
予測値
- 点推定: 1,222,458
- 区間推定(90%):1,102,110 ~ 1,344,647
- 実際の値が区間推定の中には入っており、推定に成功している