はじめに
テンソルネットワークは、量子多体系などの高次元なデータを効率的に扱うための手法として利用される技術ですが、近年、テンソルネットワークを機械学習に応用する研究が様々行われています。
今回は、文献[1]を参考に、Tree Tensor Network (TTN)を用いて、画像の分類を行うモデルをPyTorchで実装し、MNISTとFashion-MNISTに対して、その性能を確認してみます。
概要
今回用いるTree Tensor Network (TTN)は、その名の通り、木構造のテンソルネットワークです。
今回取り上げるTTNによる分類器では、葉が画像の各ピクセルに相当し、この情報を集約していくような構造になります。
この際、愚直に実装しようとすると、葉より上のノードのテンソルの次元数が非常に大きくなってしまうのですが、ここでCP分解と呼ばれる手法を用いて、これを小さなテンソルに分解します。近似的な手法ではありますが、これによりパラメータ数を抑えることができます。
今回は、この考え方に基づいて、最初から分解済みの状態でモデルを実装していき、これを用いて学習をします。
手法の確認
実装に入る前に、文献[1]で提案されている手法について確認します。
基本的な考え方
最初に、大元となる考え方から説明していきます。
今回、$N$ピクセルのグレースケール画像を$L$クラスに分類することを考えます。
まず、各ピクセルの値$x_j$を元に、以下の特徴量を考えます。量子機械学習などではよく用いられるものです。
$$ \phi(x_j)=\begin{pmatrix}
\cos(\pi x_j / 2) \
\sin(\pi x_j /2) \
\end{pmatrix} $$
次に、これらのテンソル積をとったものを画像全体の埋め込みベクトルと考えます。
$$ \Phi(\boldsymbol{x}) = \phi(x_1) \otimes \phi(x_2) ... \phi(x_N) \in \mathbb{C}^{2^N} $$
そして、分類は線形演算子$W:\mathbb{C}^{2^N} \rightarrow \mathbb{C}^{L}$を用いて行うものとします。
$$ f(\boldsymbol{x}) = W \cdot \Phi(\boldsymbol{x}) \in \mathbb{C}^{L}$$
得られた$f(\boldsymbol{x})$を正規化したものを各クラスの属する確率とします。
$$ p(l | \boldsymbol{x}) = \frac{|f_l(x)|^2}{||f(\boldsymbol{x})||^2}$$
これも量子機械学習などでよく見る考え方で、指数的な空間に持ち込んで、分類を行うモデルです。
Tree Tensor Networkの導入
先ほどのモデルを愚直に実装しようと思うと、$2^N \times L$サイズの巨大な行列を持つ必要があります。これは現実的ではないので、テンソルネットワークで表現します。
ここでは、各ノードから$b$個に枝分かれするような木構造を考えます。以下の図は、$b=2$の際の例です。
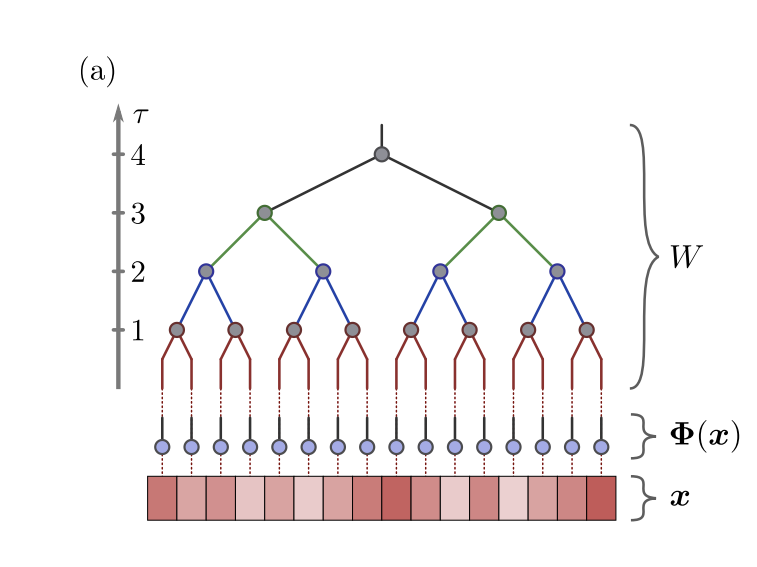
(図は文献[1] Fig1 (a)より引用)
ボンド次元を$m$とすると、葉の次に来るテンソルは以下の形で記述できます。
$$ A^{(1)}_i \in \mathbb{C}^{m} \times \mathbb{C}^{2^{b}} $$
最初の特徴量の次元が2だったため、右側は$2^b$となっています。次の層以降は、入出力ともにボンド次元になります。
$$ A^{(\tau)}_i \in \mathbb{C}^{m} \times \mathbb{C}^{m^{b}} $$
ここでは、入出力のボンド次元は等しいものとしていますが、必ずしも揃える必要はありません。また、最終層は出力の次元を分類クラス数$L$とします。
このとき、この行列を用いて各レイヤーでの計算は以下のようになります。
$$ \phi_i^{(\tau)} = A_i^{(\tau)} \cdot (\phi_{i_1}^{(\tau - 1)} \otimes \phi_{i_2}^{(\tau - 1)} \otimes ... \otimes \phi_{i_b}^{(\tau - 1)})$$
画像側のテンソルを入力として、このネットワークの計算を眺めると、最初に、$b$個のピクセルの特徴ベクトルのテンソル積をとったものに行列をかけて、$m$次元のベクトルに変換します。次の層では、この$m$次元ベクトルを$b$個集めて、テンソル積を取り、行列をかけて、また$m$次元のベクトルを作成します。これを繰り返していき、最後の層で$L$次元のベクトルを出力するような流れになります。
このとき、各レイヤーの$A_i^{(\tau)}$が学習したいパラメータに相当します。
CP分解の導入
テンソルネットワークを導入することで、ある程度保有すべきテンソルのサイズは小さくなりましたが、それでも巨大です。ここにCP分解を導入します。
CP分解では、ある高次元のテンソルをベクトルの直積の和に分解します。
具体的には、$ A^{(\tau)}_i \in \mathbb{C}^{m^{b+1}} $に対して、以下のような分解を考えます。
A^{(\tau)}_i = \sum^{r}_{k=1} \tilde{\boldsymbol{a}}_{i}^{\tau, k} \otimes \boldsymbol{a}_{i_1}^{\tau, k} \otimes \boldsymbol{a}_{i_2}^{\tau, k} \otimes ... \otimes \boldsymbol{a}_{i_b}^{\tau, k}
ただし、$ \tilde{\boldsymbol{a}}_{i}^{\tau, k}, \boldsymbol{a}_{i_j}^{\tau, k} \in \mathbb{C}^m $です。
この等式が成立する最小の$r$をcanonical polyadic rankと呼びます。
実用的には、より小さい$r$を用いて、近似的にテンソルを表現します。$r$の大きさで、精度とパラメータ数のトレードオフの関係になります。
これを用いると、各レイヤーでの演算を以下のように書き換えることができます。
\phi_i^{(\tau)} = \sum_{k=1}^{r} \tilde{\boldsymbol{a}}_{i}^{\tau, k} \psi_{i_1}^{\tau, k} \psi_{i_2}^{\tau, k} ... \psi_{i_b}^{\tau, k}
\psi_{i_n}^{\tau, k} = \sum_{\mu = 1}^{m} {a}_{i_n, \mu}^{\tau, k} \phi_{i_n, \mu}^{(\tau - 1)}
計算の流れとしては、まず、各ピクセルごとに、ベクトル成分の重み付き和を取り、その積を取ります。この値はスカラーになります。これを$\tilde{\boldsymbol{a}}_{i}^{\tau, k} $にかけます。これを$r$個繰り返したものの和が各レイヤーでの出力になります。
Tensor Dropoutの実装
過学習を抑制するため、機械学習におけるDropoutの考え方を導入するものです。
機械学習においては、モデルの学習時に、パラメータの一部を確率的に0に置き換える操作になります。
今回のTTNによる分類器では、以下の部分にこの考え方を導入します。
A^{(\tau)}_i = \frac{1}{1-p} \sum^{r}_{k=1} \lambda_{i}^{\tau, k} \tilde{\boldsymbol{a}}_{i}^{\tau, k} \otimes \boldsymbol{a}_{i_1}^{\tau, k} \otimes \boldsymbol{a}_{i_2}^{\tau, k} \otimes ... \otimes \boldsymbol{a}_{i_b}^{\tau, k}
$ \lambda_{i}^{\tau, k} $は確率$p$で0、確率$1-p$で1を取る変数です。これをTensor Dropoutと呼んでいます。
実装
上記の計算の考え方に基づき、PyTorchで分類器を実装し、学習させてみます。
データセットは文献[1]と同じく、MNISTとFashionMNISTを利用します。
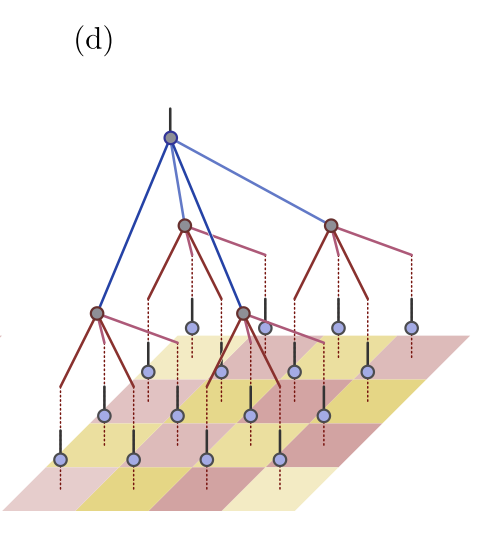
今回は$b=4$とし、画像上の$2\times2$ピクセルを各レイヤーでの入力とします。イメージ図としては、以下のような形になります。
(図は文献[1] Fig1 (d)より引用)
準備
まずは必要なライブラリをインポートします。
今回利用するライブラリのバージョンは以下の通りです。
Python 3.10.10
---
pytorch 1.12.1
torchvision 0.13.1
numpy 1.23.5
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
乱数のシードは固定しておきます。また、GPUを利用するための確認をしておきます。
np.random.seed(0)
torch.manual_seed(0)
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print(device)
続いて、データセットのMNISTを読み込みます。元論文[1]では、$16\times16$の画像を入力していたので、サイズをこれに合わせておきます。
Fashion-MNISTを利用する際は、この部分のコードのみ書き換えます。
# MNISTの読み込み
transform = torchvision.transforms.Compose([torchvision.transforms.Resize(16),
torchvision.transforms.ToTensor()])
trainval_dataset = torchvision.datasets.MNIST(root='./data',
train=True,
transform=transform,
download = True)
test_dataset = torchvision.datasets.MNIST(root='./data',
train=False,
transform=transform,
download = True)
# trainとvalidの分割
split_rate = 0.8
train_size = int(len(trainval_dataset)*split_rate)
subset1_indices = list(range(0,train_size))
subset2_indices = list(range(train_size,len(trainval_dataset)))
train_dataset = Subset(trainval_dataset, subset1_indices)
valid_dataset = Subset(trainval_dataset, subset2_indices)
# DataLoaderの準備
batch_size = 64
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
valid_loader = torch.utils.data.DataLoader(dataset=valid_dataset,
batch_size=batch_size,
shuffle=False)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
モデルの実装
PyTorchのカスタムレイヤーを使って、モデルを実装していきます。
最初に、入力画像の各ピクセルについて、特徴量変換をするレイヤーを作成します。
class Preprocess(nn.Module):
def __init__(self):
super().__init__()
def forward(self, inputs):
inputs_feature = torch.stack((torch.cos(inputs*np.pi / 2),
torch.sin(inputs*np.pi / 2)), 1)
inputs_feature = inputs_feature.reshape(-1, 2, 16, 16)
return inputs_feature
続いて、TTNのレイヤーを作成します。
class TTN_layer(nn.Module):
def __init__(self, input_size, input_dim, output_dim, branch, rank, p=0):
super().__init__()
self.branch = branch # 縮約を取るベクトル数
self.input_size = input_size # 入力画像サイズ
self.input_dim = input_dim # 入力ボンド次元
self.output_dim = output_dim # 出力ボンド次元
self.rank = rank # CP rank
self.p = p # dropout rate
self.n_cells = int(self.input_size[0] * self.input_size[1] / self.branch)
# パラメータ初期化用
std = 0.4
A_head_re = torch.randn(size=(self.rank, self.output_dim, self.n_cells), dtype=torch.float64) * std
A_head_im = torch.randn(size=(self.rank, self.output_dim, self.n_cells), dtype=torch.float64) * std
A_re = torch.randn(size=(self.rank, self.input_dim, self.branch, self.n_cells), dtype=torch.float64) * std
A_im = torch.randn(size=(self.rank, self.input_dim, self.branch, self.n_cells), dtype=torch.float64) * std
A_head = torch.complex(A_head_re, A_head_im)
A = torch.complex(A_re, A_im)
self.A_head = nn.Parameter(A_head)
self.A = nn.Parameter(A)
def forward(self, inputs):
# mapping
inputs_unfold = torch.nn.Unfold(kernel_size=(2,2),
stride=(2,2),
padding=(0,0),
dilation=(1,1))(inputs)
inputs_feature = inputs_unfold.reshape(-1, self.input_dim, self.branch, self.n_cells)
outputs = torch.einsum("ribn, xibn -> xbrn", self.A, inputs_feature.to(torch.complex128))
outputs = torch.prod(outputs, dim=1)
if self.training: # dropout
mask = torch.empty(outputs.shape).bernoulli_(1 - self.p).to(device)
outputs = outputs * mask.to(torch.complex128) / (1 - self.p)
outputs_2 = torch.einsum("ron, xrn -> xon", self.A_head, outputs)
n_output_shape = int(np.sqrt(self.n_cells))
outputs_reshape = outputs_2.reshape(-1, self.output_dim, n_output_shape, n_output_shape)
return outputs_reshape
PyTorchにデフォルトで実装されているDropoutは複素数型のテンソルをサポートしていないため、確率的に0/1を取るテンソルを作成し、複素数型に変換してから要素積を取る形で実装しています。
これらのレイヤーを組み合わせて、モデルを構築します。
今回、入力の画像は$16\times16$なので、4層の構造になります。
class TTN_Net(nn.Module):
def __init__(self):
super().__init__()
self.preprocess = Preprocess()
self.ttn_1 = TTN_layer((16, 16), 2, 8, 4, 16)
self.ttn_2 = TTN_layer((8, 8), 8, 8, 4, 16)
self.ttn_3 = TTN_layer((4, 4), 8, 8, 4, 16)
self.ttn_4 = TTN_layer((2, 2), 8, 10, 4, 16)
def forward(self, x):
x = self.preprocess(x)
x = self.ttn_1(x)
x = self.ttn_2(x)
x = self.ttn_3(x)
x = self.ttn_4(x)
x = x.reshape(-1, 10)
norm = torch.norm(x, dim=1)**2
outputs = torch.abs(x)**2 / torch.reshape(norm, (-1, 1))
return outputs.reshape(-1, 10)
TTN_net = TTN_Net()
TTN_net.to(device)
Tensor Dropoutの確率は一旦0にしています。というのも、このパラメータ設定で実行した場合、Tensor Dropoutを利用すると、性能が大きく低下してしまったためです。後ほど、Tensor Dropoutを利用した場合の効果については改めて議論します。
モデルの学習
モデルの定義ができたので、続いてモデルの学習を行います。
ここで、学習時のロス関数に加える正則化項を定義しておきます。文献[1]では、$ \sum_{\tau,i} || A_{i}^{(\tau)} ||^2 $を正則化項として利用しているため、CP分解されている状態から、元のテンソルを復元し、ノルムを取ります。
def l2_loss(params, alpha=0.01):
loss = 0
for i, p in enumerate(TTN_net.parameters()):
if i % 2 == 0:
head = p
else:
out = torch.einsum('acb,adb,aeb,afb,agb->abcdefg',
p[:,:,0,:], # [rank, b, branch, n_cells]
p[:,:,1,:],
p[:,:,2,:],
p[:,:,3,:],
head[:,:,:]) # [rank, m, n_cells])
loss += torch.norm(out)**2
return alpha*loss
実際に試してみたところでも、正則化項がない場合はパラメータが発散してしまうケースが多かったですが、正則化項を追加することで、かなり安定して学習ができるようになりました。一方で、この部分での縮約計算のコストも高く、学習時間が伸びる一因にもなっています。また、巨大なテンソルとなるため、メモリの使用量も大きいです。後述しますが、大きな$m$では、GPUのメモリ不足になりました。
学習は基本的なPyTorchの枠組みで記述できます。バリデーションデータでの性能が一番良かった時のパラメータを記録しておきます。以下のコードで学習を実行します。
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(TTN_net.parameters(), lr=1e-3)
epochs = 200
early_stop_rounds = 20
early_stop_count = 0
best_score = 0
best_params = None
loss_records_1 = []
loss_records_2 = []
for epoch in range(epochs):
TTN_net.train()
running_loss_1 = 0.0
running_loss_2 = 0.0
for i, (inputs, labels) in enumerate(train_loader, 0):
optimizer.zero_grad()
outputs = TTN_net(inputs.to(device))
loss_1 = criterion(outputs, labels.to(device))
loss_2 = l2_loss(TTN_net.parameters(), alpha=1e-4)
loss = loss_1 + loss_2
loss.backward()
optimizer.step()
# print statistics
running_loss_1 += loss_1.item()
running_loss_2 += loss_2.item()
if i % 100 == 99:
print(f"epoch: {epoch+1}\tbatch: {i+1}\tloss_1: {running_loss_1 / 100:.3f}\tloss_2: {running_loss_2 / 100:.3f}")
loss_records_1.append(running_loss_1)
loss_records_2.append(running_loss_2)
running_loss_1 = 0.0
running_loss_2 = 0.0
# validation
with torch.no_grad():
TTN_net.eval()
correct = 0
total = 0
for data in valid_loader:
images, labels = data
outputs = TTN_net(images.to(device))
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels.to(device)).sum().item()
valid_acc = 100 * correct / total
print(f"epoch: {epoch+1}\tValid Acc: {valid_acc:.2f} %")
print(f"-----------------")
if valid_acc > best_score:
best_score = valid_acc
best_params = TTN_net.state_dict()
early_stop_count = 0
else:
early_stop_count += 1
if early_stop_count >= early_stop_rounds:
print(f"Early Stopping at epoch {epoch+1}")
break
print(f"Best Valid Acc: {best_score:.2f}")
MNISTの場合、私の環境では、30epoch程度で学習はある程度収束してきており、66epoch目の98.44%が最高の結果となりました。
評価
最後に、学習済みモデルを用いて、テストデータでの性能を確認します。
TTN_net.load_state_dict(best_params)
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = TTN_net(images.to(device))
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels.to(device)).sum().item()
print(f"Test Acc: {100 * correct / total:.2f} %")
テストデータでのAccuracyは98.35%ということで、MNIST程度であれば問題なく学習できているようです。
比較実験
いくつかのパラメータについて、設定を変えながら簡単な比較を行いました。
CP rankの変化
まず最初にCPランクについてです。CPランクを大きくするほど、テンソルの近似精度としては高くなります。また、文献[1]中では、CPランクを大きくすると、精度が向上するといった実験結果が記載されています。
前述の実装では、$r=16$としていますが、$r=64$での実験を行ったところ、以下のようになりました。
Valid Acc. : 98.57 %
Test Acc. : 98.55 %
正直なところ、思ったほどの効果は確認できませんでした。
Dropoutの利用
Tensor Dropoutの実装について、$p=0.2$として実装した場合の結果です。
$r=16$の場合、テストデータでの正答率が98.35% → 97.15%と悪化しました。Fashion-MNISTの場合はより顕著で、88.14% → 79.43%まで悪化してしまいました。
おそらく、パラメータ数が少なくなり、十分な表現力を得られなくなってしまったのだと思います。
$r=64$の場合は、Dropoutの有無による大きな差はなかったのですが、基本的に利用しないほうがわずかに性能がよかったです。
全結合NNやCNNとの比較
一般的な機械学習モデルである全結合NNやCNNでの結果と精度比較をしてみました。
今回は、パラメータ数や学習時間などの条件を特に揃えておらず、ハイパーパラメータチューニングもちゃんとしていないため、あくまで参考程度に考えてください。
今回の計算環境は以下の通りです。
CPU : AMD EPYC 7V12
GPU : NVIDIA Tesla T4
AzureのNCasT4_v3シリーズのインスタンスを使っているので、詳細が気になる方はAzureのVMのドキュメント[2]をご確認ください。
以上の実験結果をまとめたものを以下に記載します。ボンド次元は$m=8$で統一してます。
MNIST
| モデル | Best Valid Acc. | Test Acc. | パラメータ数 | epoch数 | 学習時間 |
|---|---|---|---|---|---|
| TTN (r=16) | 98.44% | 98.35% | 29,856 | 86 | 27min 31sec |
| TTN (r=16) with Dropout (p=0.2) | 97.34% | 97.15% | 29,856 | 96 | 31min |
| TTN (r=64) | 98.57% | 98.55% | 119,424 | 66 | 50min 7sec |
| TTN (r=64) with Dropout (p=0.2) | 98.62% | 98.46% | 119,424 | 77 | 59min 56sec |
| 全結合NN | 98.54% | 98.37% | 793,098 | 98 | 10min 26sec |
| CNN | 99.15% | 99.10% | 83,562 | 56 | 6min 41sec |
Fashion-MNIST
| モデル | Best Valid Acc. | Test Acc. | パラメータ数 | epoch数 | 学習時間 |
|---|---|---|---|---|---|
| TTN (r=16) | 89.18% | 88.14% | 29,856 | 102 | 32min 52sec |
| TTN (r=16) with Dropout (p=0.2) | 81.03% | 79.43% | 29,856 | 60 | 19min 25sec |
| TTN (r=64) | 89.50% | 88.39% | 119,424 | 72 | 54min 32sec |
| TTN (r=64) with Dropout (p=0.2) | 89.32% | 88.02% | 119,424 | 121 | 1h 33min 49sec |
| 全結合NN | 90.73% | 89.64% | 793,098 | 120 | 12min 48sec |
| CNN | 90.66% | 90.06% | 83,562 | 79 | 9min 6sec |
どちらのデータセットでも、CNNが最も良い性能となりました。TTNと全結合NNについては、MNISTにおいては、TTNで$r=64$の場合に全結合NNを超える結果となりましたが、Fashion-MNISTの場合は、常に全結合NNにも劣る結果になってしまったのは少し残念です。もっと巨大なモデルにすれば勝てるのかもしれませんが、学習時間が伸びやすいのが辛いところです。
また、今回はDropoutの実装はわずかに性能を落とす結果になってしまいました。過学習の抑制という観点でも、あまり機能しているようには見えません。こちらも、より大きなモデルであれば有効的に働くのかもしれません。
文献[1]に記載されている実験結果では、Fashion-MNISTに対し、dropoutなしのTTNが88.5%、dropoutありの場合は90.3%の正答率が出たと記載されています。dropoutなしの場合の数値は、概ね今回の私の実装と一致しているので、このぐらいの上昇余地はあるのかもしれません。文献[1]に記載されているものを見ると、$m=16,r=64,p=0.3$でこの結果が得られたとのことですが、私の環境では$m=16, r=64$では、正則化項の計算部分でテンソルが巨大になり、GPUのメモリ不足になってしまったため、検証は断念しています。T4のGPUメモリは16GBあるのですが、まさかMNISTの検証で不足することになるとは思いませんでした。
参考までに、全結合NNとCNNの実装は以下です。
# 全結合NN
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(16*16, 1024)
self.fc2 = nn.Linear(1024, 512)
self.fc3 = nn.Linear(512, 10)
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
x = x.reshape(-1, 16*16)
x = F.relu(self.fc1(x))
x = self.dropout(x)
x = F.relu(self.fc2(x))
x = self.dropout(x)
x = self.fc3(x)
return x
# CNN
class Net_2(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 32, (2, 2))
self.conv2 = nn.Conv2d(32, 64, (2, 2))
self.pool = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(3 * 3 * 64, 128)
self.fc2 = nn.Linear(128, 10)
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
x = F.relu(self.pool(self.conv1(x)))
x = F.relu(self.pool(self.conv2(x)))
x = self.dropout(x)
x = x.reshape(-1, 3*3*64)
x = F.relu(self.fc1(x))
x = self.dropout(x)
x = self.fc2(x)
return x
所感
今回は、Tree Tensor Networkを用いた画像分類機を作成し、MNISTとFashionMNISTの分類を試してみました。
TTNにおける縮約計算は、近傍のピクセルから情報を集約していき、小さい画像のようなものにしていく計算となっており、CNNの考え方に近いものを感じます。一方、CNNは同じフィルタをスライドさせながら使っていくのに対し、今回のモデルはピクセルごとに別々の重みをかけていくものになっています。全結合NNのように遠くのピクセル同士の線形和は出てこないので、強いて言うのであれば、全結合NNとCNNの中間のような挙動でしょうか。
また、CNNにおけるPooling操作では、最大値や平均値を用いることが多いですが、今回の場合、積を取るような操作がPoolingに相当します。このため、値が消失/発散しやすく、ハイパーパラメータの調整をきちんとしないと、学習が不安定になる印象を受けました。今回の実装では、float64を用いていますが、これはfloat32を用いた際には、重みが消失/発散してしまうケースが散見されたためです。
今回のモデルの最大の課題点は計算時間とメモリ使用量だと思います。正則化項を用意しないとうまく学習できないのですが、この部分でテンソルの縮約計算を行う必要があり、非常に巨大なテンソルを持つ必要があるため、計算時間とメモリ使用量が大きく膨らみます。分解された状態のテンソルに対して、同様にL2正則化項を行うことも試してみたのですが、こちらではうまく学習が進みませんでした。
今回の検証では、MNIST、FashionMNISTといったグレースケールの比較的簡単な画像分類タスクを行いましたが、CIFAR-10やImageNetといった、より広いクラスのカラー画像を扱うタスクでどの程度性能が出せるのかなども気になるところです。