統計学では、世の中で起こる出来事の結果を確率変数 (random variable) と呼びます。そして、それぞれの確率変数の起こりやすさを与えてくれるのが確率分布 (probability distribution) です。
確率変数はそれがどんな出来事の結果であるかにより、確率変数が属する確率分布の形が変わってきます。以下に、確率分布を描画するPythonでのコード付きで、統計学で良く用いられる確率分布をまとめました。
確率変数が離散値のとき
ある出来事の結果$X$ が、とびとびの値をとる場合です。各分布の例として、確率質量関数 (probability mass function) のグラフを載せています。
確率質量関数とは、各$X$ について、それぞれの確率を与える関数です。
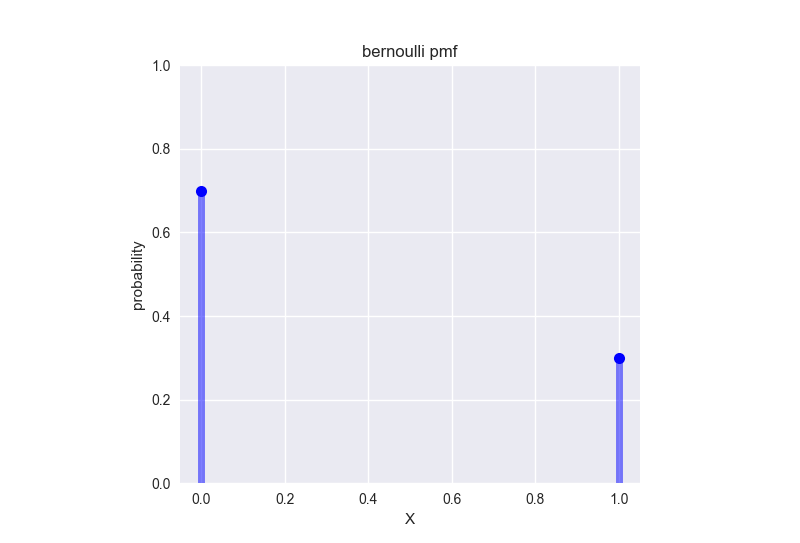
ベルヌーイ分布 (Bernoulli distribution)
ある事象Xが、$X = 0$ or $X = 1$ の2通りのみの結果しかありえないとします。このとき、$P(X=1) = p$ だとすると、確率変数$X$ はベルヌーイ分布 (Bernoulli distribution) に従います。
もし、確率変数$X$ が確率$p$ のベルヌーイ分布に従うなら ($X$ ~ $B(p)$)、以下が成り立ちます。
\begin{align}
P(X=1) &= p \\
P(X=0) &= 1 - p \\
E[X] &= p \\
Var(X) &= p(1-p)
\end{align}
このとき、$E[X]$ は平均、$Var(X)$ は分散を表します。
例として、合格率30%の試験を一度受けたとき、その結果の確率質量関数を示します。
## Bernoulli distribution ---------------------------------------------
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import bernoulli
# probability that X=1
p = 0.3
# possible outcomes
x = [0,1]
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(x, bernoulli.pmf(x, p), 'bo', ms=8)
ax.vlines(x, 0, bernoulli.pmf(x,p), colors='b', lw=5, alpha=0.5)
ax.set_xlabel('X')
ax.set_ylabel('probability')
ax.set_title('bernoulli pmf')
ax.set_ylim((0,1))
ax.set_aspect('equal')
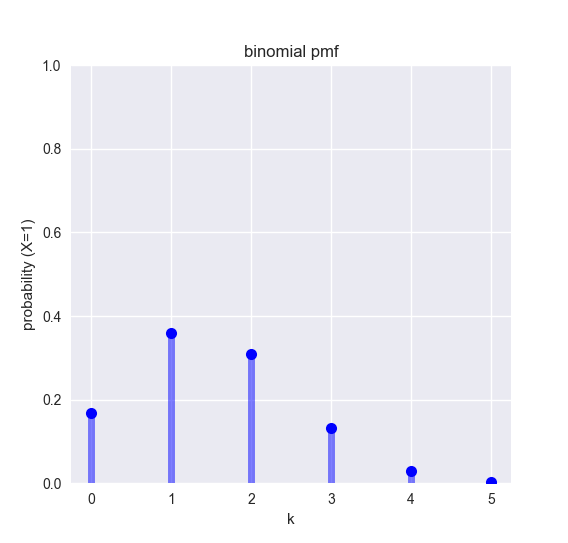
二項分布 (Binomial distribution)
二項分布はベルヌーイ分布を一般化したものです。$N$回のベルヌーイ試行をただ足し合わせたものです。$N$回の試行のうち、確率$p$ の 事象$X$ が$k$ 回起こる確率分布を表現します。
$X$ ~ $Bin(N, p)$ のとき、
\begin{align}
P(X=k|p) &= \binom{N}{k} p^{k}(1-p)^{N-k} \\
E[X] &= np \\
Var(X) &= np(1-p)
\end{align}
例として、合格率30%の試験を5回受けたとき、受かる回数ごとの確率を表す確率質量関数を示します。
## Binomial distribution ---------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import binom
# probability that X=1
p = 0.3
# the number of trials
N = 5
# X=1 happens k times
k = np.arange(N+1)
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(k, binom.pmf(k, N, p), 'bo', ms=8)
ax.vlines(k, 0, binom.pmf(k, N, p), colors='b', lw=5, alpha=0.5)
ax.set_xlabel('k')
ax.set_ylabel('probability (X=1)')
ax.set_title('binomial pmf')
ax.set_ylim((0,1))
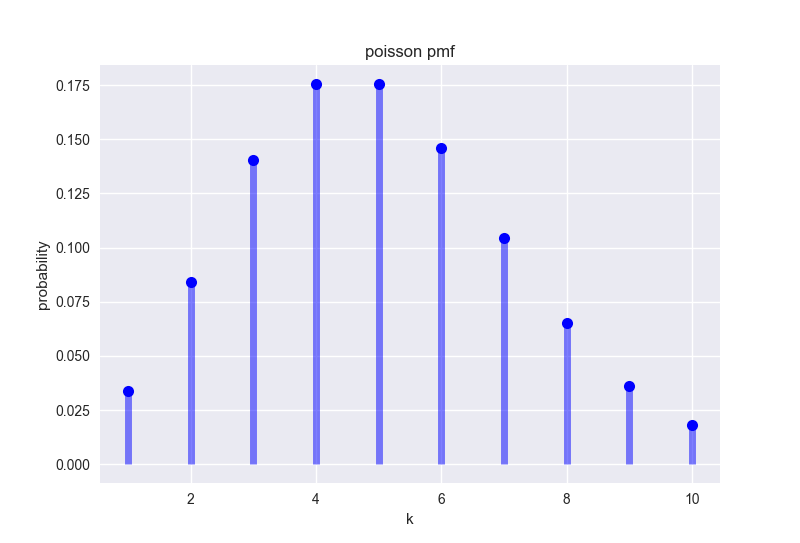
ポワソン分布 (Poisson distribution)
ポワソン分布は、ある出来事が起こる回数を表現するために使われます。パラメーターは、その出来事の平均頻度を表す$\lambda$のみです。
$X \sim Pois(\lambda)$ のとき、
\begin{align}
P(X=k|\lambda) &= \frac{\lambda^{k} e^{-\lambda}}{k!} \hspace{15pt} for \hspace{10pt} k = 0, 1, 2, ...\\
E[X] &= \lambda \\
Var(X) &= \lambda
\end{align}
ポワソン分布では、平均 = 分散 = $\lambda$ なのが特徴的です。
例として、神経細胞の発火頻度が挙げられます。神経細胞の発火活動はおおよそポワソン過程であることが知られており、ある神経細胞の平均発火率が5 (times/s) であるとすると、この神経細胞の1秒間の発火回数は、以下のような確率分布になります。
## Poisson distribution --------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import poisson
# rate parameter
mu = 5
# possible counts
k = np.arange(poisson.ppf(0.01, mu), poisson.ppf(0.99, mu))
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(k, poisson.pmf(k, mu), 'bo', ms=8)
ax.vlines(k, 0, poisson.pmf(k, mu), colors='b', lw=5, alpha=0.5)
ax.set_xlabel('k')
ax.set_ylabel('probability')
ax.set_title('poisson pmf')
確率変数が連続値のとき
ある出来事の結果$X$ が、とびとびではなく連続した値をとる場合です。各分布の例として、確率密度関数 (probability density function) のグラフを載せています。
確率密度関数は確率質量関数とは異なり、各$X$ について、それぞれの相対尤度(相対的な起こりやすさ)を与える関数です。$X$ が範囲 $a \leq X \leq b$ をとるときの確率は、その範囲の確率密度関数の面積、つまり積分$\int_{a}^{b} f(X) dX$ で求められます。確率の定義上、確率密度関数の全範囲 $-\inf \leq X \leq \inf$ の面積は1になります。
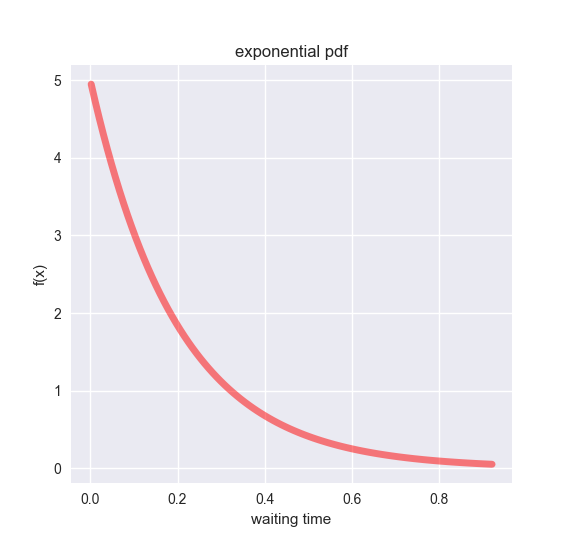
指数分布 (Exponential distribution)
指数分布は、ある出来事が何度も起きるとき、ある出来事とある出来事の間にどれだけの時間が流れたかを表現します。要は、待ち時間の分布ですね。
より統計学的に言うと、ポワソン過程間の時間を表現します。そのため、パラメーターもポワソンと同様、平均頻度を表す$\lambda$ です。
$X \sim Exp(\lambda)$ のとき、
\begin{align}
f(x|\lambda) &= \lambda e^{-\lambda x} \hspace{15pt} (x \geq 0) \\
E[X] &= \frac{1}{\lambda} \\
Var(X) &= \frac{1}{\lambda^{2}}
\end{align}
つまり、ある出来事がポワソン過程なら、それが起きてから次起こるまでの平均待ち時間は$1/\lambda$ だということですね。
以下は、先ほどの神経細胞が発火してから、次に発火するまでの時間の分布を指数分布で示しています。
## Exponential distribution --------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import expon
# rate parameter
mu = 5
# possible waiting time
k = np.linspace(expon.ppf(0.01, loc=0, scale=1/mu), expon.ppf(0.99, loc=0, scale=1/mu), 100)
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(k, expon.pdf(k, loc=0, scale=1/mu), 'r-', lw=5, alpha=0.5)
ax.set_xlabel('waiting time')
ax.set_ylabel('f(x)')
ax.set_title('exponential pdf')
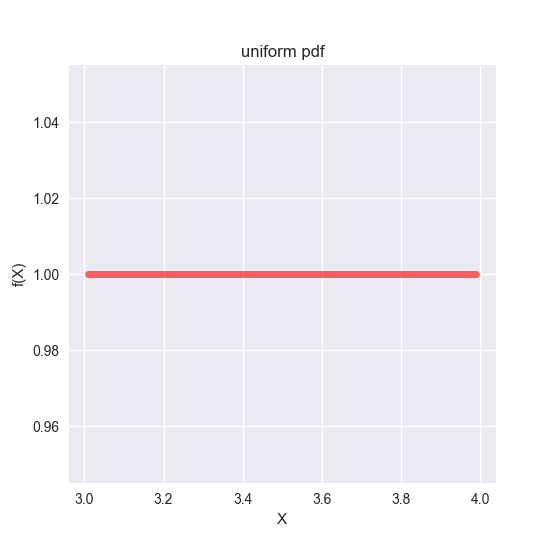
一様分布 (Uniform distribution)
一様分布は最も単純な形の分布ですが、規定の範囲内のどの確率変数$x$でも同じ値の確率を返すため、起こりうる結果が同様に確からしいときに必須な確率分布です。
$X$ ~ $U[a,b]$ のとき、以下が成り立ちます。
\begin{align}
f(x) &= \frac{1}{b - a} \hspace{15pt} if \hspace{15pt} a \leq x \leq b \\
f(x) &= 0 \hspace{45pt} otherwise \\
E[X] &= \frac{a + b}{2} \\
Var(X) &= \frac{(b - a)^{2}}{12}
\end{align}
また、一様分布の平均について、「平均の和は和の平均」、「平均の積は積の平均」(ただし事象が独立しているとき)が成り立ちます。
\begin{align}
E[X+Y] &= E[X] + E[Y] \\
E[XY] &= E[X]E[Y] \hspace{20pt} (if \hspace{5pt} X \perp Y)
\end{align}
例として、ある実験結果が3から4の連続値のうちのどれかの値を取るはずで、それぞれの確率が同様に確からしいときの確率密度関数を示します。
## Uniform distribution ---------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import uniform
# range
a = 3
b = 4 - a
x = np.linspace(uniform.ppf(0.01, loc=a, scale=b), uniform.ppf(0.99, loc=a, scale=b), 100)
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(x, uniform.pdf(x, loc=a, scale=b), 'r-', alpha=0.6, lw=5)
ax.set_xlabel('X')
ax.set_ylabel('P(X)')
ax.set_title('uniform pdf')
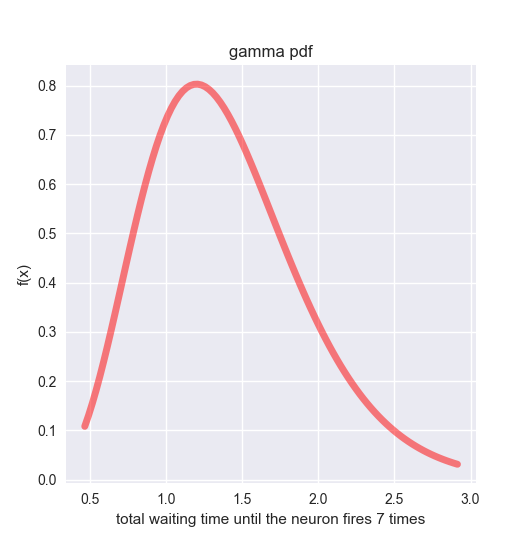
ガンマ分布 (Gamma distribution)
ガンマ分布 は、ある出来事が$n$ 回起こるときの、総待ち時間の分布を表現します。そのため、$n = 1$ ならガンマ分布は指数分布と一致します。パラメーターは、$\alpha = n$, $\beta = \lambda$ の2つです。$\lambda$ はポワソン分布や指数分布と同様、出来事の平均頻度ですね。
$X \sim Gamma(\alpha, \beta)$ のとき、以下が成り立ちます。
\begin{align}
f(x|\alpha, \beta) &= \frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x} \hspace{20pt} (x \geq 0) \\
E[X] &= \frac{\alpha}{\beta} \\
Var[X] &= \frac{\alpha}{\beta^{2}} \\
\end{align}
式中に出てくる**$\Gamma(・)$** はガンマ関数 と呼ばれ、実は階乗 $(!)$ の一般系です。以下の式が成り立ちます。
if \hspace{10pt} n > 0 \\
\Gamma(n) = (n-1)!
このガンマ関数、右側に尾を引いた (right-skewed)分布のモデルに使われるのですが、階乗との関連もあり、統計学ではよく出てくる分布です。
以下は、$\alpha = 7, \beta = 5$ のときのガンマ分布です。例の神経細胞が7回発火するまでの総待ち時間の分布だと解釈してください。
## Gamma distribution --------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import gamma
# total number of events
n = 7
# rate parameter
mu = 5
# possible waiting time
x = np.linspace(gamma.ppf(0.01, n, loc=0, scale=1/mu), gamma.ppf(0.99, n, loc=0, scale=1/mu), 100)
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(x, gamma.pdf(x, n, loc=0, scale=1/mu), 'r-', lw=5, alpha=0.5)
ax.set_xlabel('total waiting time until the neuron fires 7 times')
ax.set_ylabel('f(x)')
ax.set_title('gamma pdf')
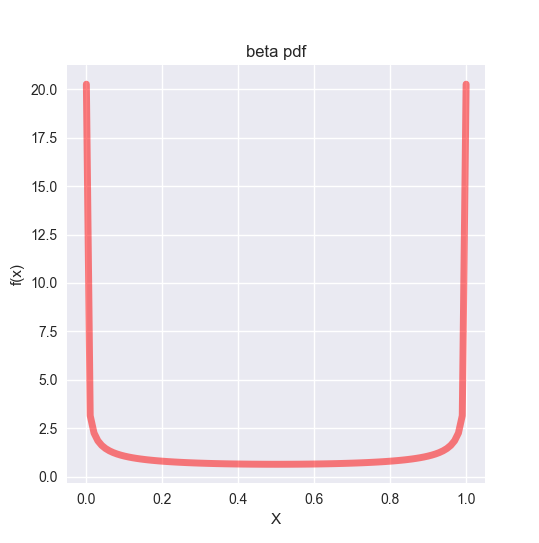
ベータ分布 (Beta distribution)
ベータ分布 は $0 \leq X \leq 1$ となる変数$X$ を表現するために使われます。つ
まり、確率自体をモデル化することができます。
$X \sim Beta(\alpha, \beta)$ のとき、以下が成り立ちます。
\begin{align}
f(x|\alpha, \beta) &= \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)}x^{\alpha-1}(1 - x)^{\beta - 1} \hspace{10pt} (0 \leq x \leq 1) \\
E[X] &= \frac{\alpha}{\alpha + \beta} \\
Var[X] &= \frac{\alpha \beta}{(\alpha + \beta)^{2}(\alpha + \beta + 1)}
\end{align}
一見複雑な式ですが、意外なことに $\alpha = \beta = 1$ のとき、ベータ分布は一様分布$U(0,1)$ に一致します。
例として、$\alpha = \beta = 0.5$ のときのベータ分布を見てみましょう。ベータ分布はパラメーターによって多彩な形状を表現できますが、このときは谷(?)のような特徴的な分布になります。
## Beta distribution --------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import beta
# parameters
a = 0.5
b = 0.5
# range
x = np.linspace(beta.ppf(0.01, a, b), beta.ppf(0.99, a, b), 100)
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(x, beta.pdf(x, a, b), 'r-', lw=5, alpha=0.5)
ax.set_xlabel('X')
ax.set_ylabel('f(x)')
ax.set_title('beta pdf')
ベータ分布は本来、「一様分布に従う確率変数$X(0 \leq X \leq 1)$ を大きい順に並べたとき、下から$p$ 番目の数の分布が、ベータ分布$Beta(p,q)$ になる」という意味を持っています。ただ、少なくとも統計学における主な使い道は自然共益分布としてベイズ更新なので、大事なのはその意味ではなく、ベータ分布が取りうる形状が多様であることにあります。以下、いろいろなパラメータの組み合わせでベータ分布を描画したものをプロットしました。
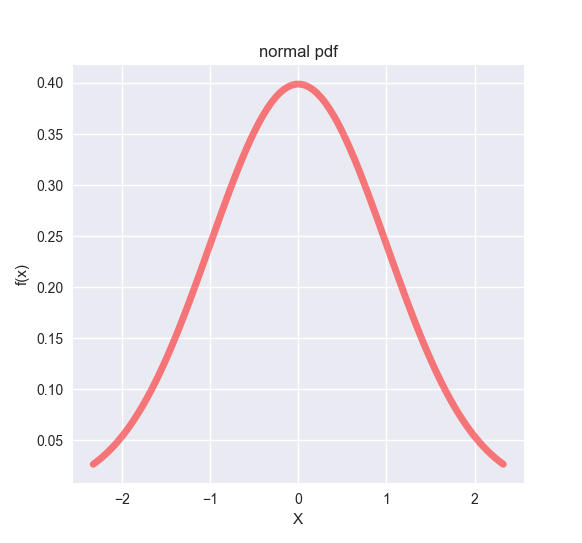
正規分布 (Normal distribution)
いよいよ正規分布 (ガウス分布)です。中心極限定理 (Central Limit Theorem: 母集団がどのような分布でも、標本平均の真の平均の誤差の分布は、試行が十分多ければ正規分布に近づく) でも大事なように、統計学では避けては通れない確率分布です。
$X \sim N(\mu , \sigma^{2})$ のとき、以下が成り立ちます。
\begin{align}
f(X|\mu, \sigma^{2}) &= \frac{1}{\sqrt{2 \pi \sigma^{2}}} exp{^\frac{(x - \mu)^{2}}{2 \sigma^2}} \\
E[X] &= \mu \\
Var(X) &= \sigma^{2}
\end{align}
正規分布では、標準偏差$\sigma$の3倍の範囲内に99%以上のデータ$X$ が含まれます。ですので、ある変数が標準偏差$\sigma$の3倍の範囲外であれば、外れ値 (outlier) であると判定されます。
また、独立した複数の正規分布について、以下が成り立ちます。
if \hspace{10pt} X1 \sim N(\mu_1, \sigma_1^{2}) \perp X2 \sim N(\mu_2, \sigma_2^{2}) \\
\\
X1 + X2 \sim N(\mu_1 + \mu_2, \sigma_1^{2} + \sigma_2^{2})
独立した正規分布から得られた変数同士の和は、元の平均の和、分散の和を持つ新しい正規分布に従うのですね。
グラフの例として、$\mu = 0, \sigma^{2} = 1$ つまり標準正規分布 (z-distribution) を示します。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
# mean
mu = 0
# standard deviation
sd = 1
# range
x = np.linspace(norm.ppf(0.01, loc=mu, scale=sd), norm.ppf(0.99, loc=mu, scale=sd), 100)
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(x, norm.pdf(x, loc=mu, scale=sd), 'r-', lw=5, alpha=0.5)
ax.set_xlabel('X')
ax.set_ylabel('f(x)')
ax.set_title('normal pdf')
標準正規分布において、95%のデータが含まれる範囲の端の値が**$\pm 1.96$**だという事実は覚えておいて損はないです。これを越える値は、+側ならだいたい偏差値70以上に相当するレアキャラ(全体の2.5%程度)ですね。
ちなみに偏差値を計算するときには、テストの点数を$N(50, 10^{2})$ となるように規格化しています。以下が、テストの得点分布が$N(\mu_x, \sigma_x^{2})$であるときの、テスト$x_i$ 点を偏差値$T_i$ に変換する公式です。
T_i = \frac{10(x_i - \mu_x)}{\sigma_x} + 50
T分布 (T distribution)
最後はT分布です。T検定 (T test) は2群の平均値が有意に違っているかを検定する便利な方法で、よく理解がされないまま特にバイオの世界で乱用されているので、ここでもう一度T分布とは何ぞやというのを復習したいと思います。
仮に、実験データ$X$ が正規分布$N(\mu, \sigma^{2})$ に従う母集団から得られた、とします。
X \sim N(\mu, \sigma^{2})
このとき、実験データ$X$ の平均値$\overline{X}$ は、$X = X_1, X_2, ..., X_n$ が互いに独立で同一の確率分布から得られた (independent and identically distributed; iid) と考えられるので、独立した正規分布の性質により、
\begin{align}
\Sigma_{i=1}^{n} X_i &\sim N(n*\mu, n*\sigma^{2}) \\
\frac{1}{n}\Sigma_{i=1}^{n} X_i &\sim N(\mu, \frac{\sigma^{2}}{n}) \\
\overline{X} &\sim N(\mu, \frac{\sigma^{2}}{n}) \\
\frac{\overline{X} - \mu}{\sigma /\sqrt{n}} &\sim N(0,1)
\end{align}
と変形していけます。このとき、標準化されたデータ平均値が標準正規分布においてデータの95%が含まれる端の値、$1.96$ よりも大きかったり、$-1.96$ よりも小さければ、標本平均$\overline{X}$ は母集団の平均から有意に離れている と言っていいでしょう…………というのがZ検定 です。
実際には、母集団の標準偏差$\sigma$ は標本データから知りえないことが多く(Z検定は不適格)、代わりに標本から推定された母集団の標準偏差(不偏分散)S を用います。普通、標準偏差の計算ではデータと平均の差の二乗を足し合わせ、データ数$n$ で割って平方根をとったものを使いますが、不偏分散の計算では$n$ ではなく$n-1$ で割ります。
S = \sqrt{\Sigma_{i}(X_i - \overline{X})^{2}/(n-1)}
この簡単な処理で、標本から推定した母集団の標準偏差の期待値を、母集団の標準偏差と一致させることができます。
ただ、ここまでいじってしまうと、標準化した$\overline{X}$ は正規分布に従うことはもうありません。その代わり、自由度$n-1$ のt分布に従うことになります。
$Y \sim t_{\gamma}$ のとき、以下が成り立ちます。
\begin{align}
f(y) &= \frac{\Gamma(\frac{\gamma + 1}{2})}{\Gamma(\frac{\gamma}{2})\sqrt{\gamma \pi}}(1 + \frac{y^{2}}{\gamma})^{-\frac{\gamma + 1}{2}} \\
E[Y] &= 0 \hspace{10pt} if \hspace{10pt} \gamma \geq 1 \\
Var[Y] &= \frac{\gamma}{\gamma-2} \hspace{10pt} if \hspace{10pt} \gamma \geq 2 \\
\end{align}
これで実験平均$\overline{x}$ から変換された$t$ 値が、データの自由度によって決まるT分布において、全体の95%のデータが含まれる端の値より大きかったり小さかったりすれば、母集団と標本の平均の差について有意検定をすることができる、というのがT検定です。
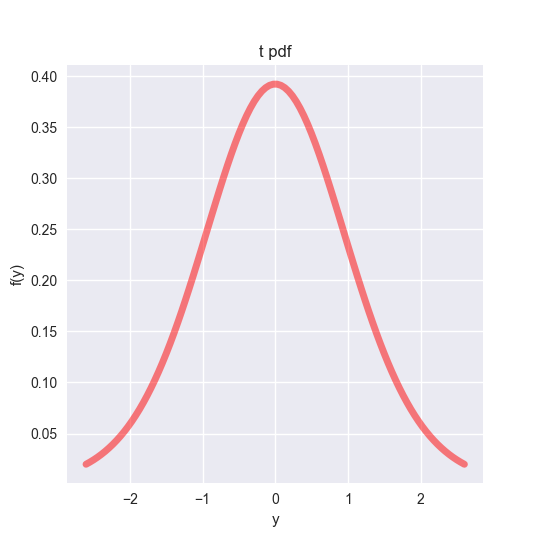
グラフとして、自由度15のT分布を載せておきます。T分布も正規分布に近い形をしていますが、やや幅広な傾向があります。自由度が上がるにつれ、正規分布に近づいていきます。
## t distribution --------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import t
# degree of freedom
df = 15
# range
x = np.linspace(t.ppf(0.01, df), t.ppf(0.99, df), 100)
# visualize
fig, ax = plt.subplots(1,1)
ax.plot(x, t.pdf(x, df), 'r-', lw=5, alpha=0.5)
ax.set_xlabel('y')
ax.set_ylabel('f(y)')
ax.set_title('t pdf')
おわりに
統計学やデータ解析でよく登場する確率分布をまとめましたが、もちろん世の中にはもっとたくさんの種類の確率分布があります。もし時間があれば追加していきたいと思います。