この記事はニフティグループ Advent Calendar 2020の16日目の記事です。
昨日は @hajimete さんのNode.jsでプランニングポーカー自作してみたでした。
もしスクラム開発の機会が巡ってきた際には使わせていただきます!
はじめに
現在、弊社ではデータ分析の動きが広まっており、自分もプロジェクトに参加してデータを分析しています。
今回は最近学んだ統計学の手法の一つである一般化線形モデルについて、頭の整理も兼ねてまとめてみました。
一般化線形モデルとは何か、モデリングに必要な作業、作成したモデルの評価方法について触れていきます。
もし間違いや気になる点などありましたらコメントいただけると嬉しいです!
主に以下の文献を参考にさせていただきました。
一般化線形モデル(GLM) とは
一般化線形モデル(General Linear Model、GLM)とは、統計学の枠組みを利用してモデル作成を行う手法の一つです。分析対象のデータ分布を参考に、以下の三つを設定してモデリングを行います。
- 確率分布
- リンク関数
- 線形予測子
上の三つを設定した後は、最尤推定法と呼ばれるものでモデルを作成し、その後作成したモデルの評価を行います。
確率分布とは
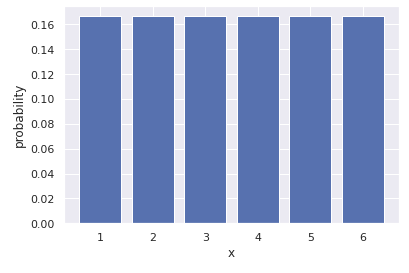
確率変数が取る値と、その値が得られる確率を対応づけたもの。
- 例えばサイコロなら、確率変数は 1 から 6 までの6つの整数を取り、それぞれの目が出る確率は 1/6 なので、確率分布は下のようなものになります。
GLM では、目的変数の残差を確率変数として、残差が従う確率分布を仮定します。
残差と確率分布
残差とは、予測値と実際のデータの差分のことです。
線形回帰を例にとると、目的変数の分布に対して以下のような回帰直線を引いたとします。この時、直線とデータ点との距離が予測した値(回帰直線上の点)と実際のデータ点の差分であり、これが残差と呼ばれます。
この残差の値が正規分布に従っている場合、回帰直線の周りにデータが多く集まっているため、データ点に対して線形回帰の精度は高くなります。逆に残差が正規分布に従っていない場合は、データのばらつきが大きいということで回帰直線でフィッティングできず、精度は悪くなります。
GLM では残差の従う確率分布として正規分布以外のものを用いることができ、様々な残差の分布に対応したモデリングが可能です。
どの確率分布を用いれば良いかは、目的変数の特性からある程度決まっています。
- ポアソン分布:データが離散値、非負の値、上限はなし、平均と分散がほぼ同じ。
- 二項分布:データが離散値、非負の値、有限の範囲内、分散は平均の関数。
- ベルヌーイ分布:データが離散値、二値の値のみをとる、有限の範囲内、分散は平均の関数。
- 正規分布:データが連続値、範囲が $[-\infty, +\infty]$、分散は平均とは無関係。
- ガンマ分布:データが連続値、範囲が $[0, +\infty]$、分散は平均の関数。
リンク関数と線形予測子
リンク関数とは、目的変数 $y_i$ と説明変数を紐づけたもので、データ点へフィッティングされる関数です。一般的に下のように記述できます。
$f(y_i)=\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_kx_k+...$ (1)
$f$:リンク関数
(1) 式の右辺が線形予測子と呼ばれ、説明変数 $x_i$ と対応したパラメータ $\beta_i$ $(i=1, 2, ...)$の積の和で表されます。
線形予測子は、(1) 左辺の目的変数に対してどの説明変数を考慮するのか、何乗で聞いてくるのかなどの「効き方」を設定します。
- 説明変数に関しては $\log{x_i}$ のように変換したものを用いる場合もあります。
- ただし、パラメータ $\beta_i$ の線型結合であることに注意して下さい。
GLM の際には確率分布とその分布に対応したリンク関数を選びます。こちらも確率分布同様に対応が決まっています。
- ポアソン分布:対数リンク関数
- 二項分布:ロジットリンク関数
- ベルヌーイ分布:ロジットリンク関数
- 正規分布:恒等リンク関数
- ガンマ関数:対数リンク関数
ここから、参考文献で扱っている架空のデータを基に、実際のGLMの動きを見ていきます。
例:植物個体から取得できる種子数をモデリングする
参考文献で利用しているデータの条件をそのまま拝借します。
ある架空の植物から得られる種子数とその植物の大きさのデータセットが与えられているとします。ある一つの植物個体 $i$ における、植物の大きさ $x_i$に対して得られる種子数の数 $y_i$ をモデリングしたいとします。また、$y_i$ に上限はないとします。
- 目的変数:種子数 $y_i$
- 説明変数:植物の大きさ $x_i$
確率分布の設定
種子数 $y_i$ は非負の離散値で上限がないことから、確率分布としてポアソン分布を仮定してみます。
ポアソン分布は次の式で表されます。
$p(y_i|\lambda_i)=\frac{\lambda_i^{y_i}\exp{(-\lambda_i)}}{y_i!}$
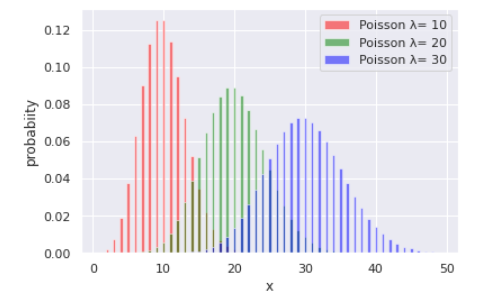
ここで $\lambda_i$ は植物から取得できる平均種子数で、ポアソン分布の平均値であり、ポアソン分布の形に影響するパラメータです。$\lambda_i$ の値によってポアソン分布の形が変化することを下のコードで確認します。
from scipy.stats import poisson
x = np.arange(1, 50, 1)
y1= [poisson.pmf(i, 10) for i in x]
y2= [poisson.pmf(i, 20) for i in x]
y3= [poisson.pmf(i, 30) for i in x]
plt.bar(x, y1, align="center", width=0.4, color="red"
,alpha=0.5, label="Poisson λ= %d" % 10)
plt.bar(x, y2, align="center", width=0.4, color="green"
,alpha=0.5, label="Poisson λ= %d" % 20)
plt.bar(x, y3, align="center", width=0.4, color="blue"
,alpha=0.5, label="Poisson λ= %d" % 30)
plt.xlabel("x")
plt.ylabel("probability")
plt.legend()
plt.show()
上の図のように、ポアソン分布はパラメータ $\lambda_i$ によって分布が変わることが分かります。
平均種子数 $\lambda_i$ が与えられると、植物個体 $i$ から取得できる種子数 $y_i$ が従う確率分布を得ることができます。
ポアソン分布のリンク関数・線形予測子
ポアソン分布のリンク関数と線形予測子を決めていきます。これは計算のしやすさなどからほぼ形が決まっており、ポアソン分布の場合は以下のように設定します。
$\log{\lambda_i}=\beta_0+\beta_1x_i$
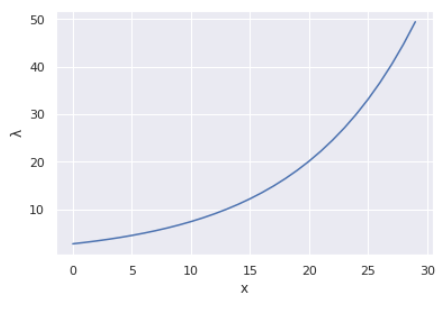
これを変形すると $\lambda_i=\exp{(\beta_0+\beta_1x_i)}$ となります。植物の大きさ $x_i$ とパラメータ $\beta_i$ から平均種子数 $\lambda_i$ が得られ、大きさ $x_i$ の植物個体が従うポアソン分布が求まります。
$\lambda_i$ と $x_i$ の関係性をプロットしてみます。
# 平均種子数と体の大きさの関係を図示
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 30, 1)
beta_0 = 1
beta_1 = 0.1
lam = np.exp(beta_0 + beta_1*x)
plt.plot(x, lam)
plt.xlabel("x")
plt.ylabel("λ")
plt.show()
この曲線が、$(x_i, y_i)$ のデータセットに対して引こうとしている(モデリングしようとしている)曲線になります。
最後にまだ未定なパラメータ $\beta_i$ の値は最尤推定法によって推定します。
最尤推定法によるパラメータ推定
尤度と呼ばれる「手元のデータに対する当てはまりの良さ」を表す量を定義し、それが最大となるパラメータを求める手法が最尤推定法です。詳しい説明は省略しますが、今回の例における尤度を示します。
ポアソン分布の場合、尤度は次のようにパラメータ $\beta_i$ の関数として表されます。
$L(\beta_0, \beta_1)=\prod_ip(y_i|\lambda_i)=\prod_i \frac{\lambda^y_i \exp(-\lambda)}{y_i!}$
簡単のため、ログをとった対数尤度というものがよく用いられる。
$\log{L}=\sum_i\log{(p(y_i|\lambda_i))}=\sum_i(y_i\log{\lambda}-\lambda-\sum_k^{y_i}\log{k})$
$\lambda_i=\exp{(\beta_0+\beta_1x_i)}$
この対数尤度が最大となるようなパラメータ $\beta_i$ を求めます。
モデル評価
モデルの評価について簡単に説明します。
フィッティングを行う際、最尤推定法を用いて、対数尤度が最大になるパラメータの値を推定しました。しかしこの対数尤度の最大値(最大対数尤度)は、手元のデータに対する当てはまりの良さを表しています。そのため、未知のデータに対しては予測精度が下がる可能性が考えられます。統計モデリングでは、「予測の良さ」を表すことができるAICという量の大きさを比較して、複数のモデルの評価を行います。AICに関する詳しい説明は省略させていただきますが、AICが低いほど予測の良いモデルということができます。
Python で GLM を実践
以下では python でGLM する方法を簡単に見ていきます。
statsmodel という python ライブラリを用いて、ボストン住宅価格データに対し GLM を行います。
住宅の平均部屋数(カラム名:RM)に対する住宅価格(カラム名:PRICE)をモデリングします。
指定する確率分布を変えた時の AIC を比較します。
実行環境
Google Colaboratory
ライブラリインポート
# 基本的なライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
# statsmodel
import statsmodels.api as sm
import statsmodels.formula.api as smf
# ボストン住宅価格データのインポート
from sklearn.datasets import load_boston
データ準備
# データをデータフレーム型に変換
boston = load_boston()
boston_df = pd.DataFrame(boston.data, columns=boston.feature_names)
# 説明変数 x と目的変数 y を準備
boston_df["PRICE"] = boston.target
x = boston_df.drop("PRICE", axis=1)
y = boston_df["PRICE"]
ボストン住宅価格データセットの説明変数を確認してみます。
# ボストンデータセットのカラムの説明
print(boston.DESCR)
CRIM per capita crime rate by town
ZN proportion of residential land zoned for lots over 25,000 sq.ft.
INDUS proportion of non-retail business acres per town
CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
NOX nitric oxides concentration (parts per 10 million)
RM average number of rooms per dwelling
AGE proportion of owner-occupied units built prior to 1940
DIS weighted distances to five Boston employment centres
RAD index of accessibility to radial highways
TAX full-value property-tax rate per $10,000
PTRATIO pupil-teacher ratio by town
B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
LSTAT % lower status of the population
MEDV Median value of owner-occupied homes in $1000's
PRICE と RM の散布図をプロットしてみます。
column = "RM"
sns.scatterplot(x="PRICE", y=column, data=boston_df[["PRICE", column]])
比較的直線でフィッティングできそうな分布をしていることが分かります。
モデリング
いよいよモデリングを行います。上で色々と説明しましたが、実装自体はライブラリのおかげて非常にシンプルに行うことができます。
# 説明変数と目的変数を一つの行列にする
data = boston_df
# 線形予測子を定義
formula = "PRICE ~ 1 + RM"
# リンク関数を設定
link = sm.genmod.families.links.log
link_gauss = sm.genmod.families.links.identity
# 確率分布を設定
family = sm.families.Poisson(link=link)
family_gauss = sm.families.Gaussian(link=link_gauss)
# モデリング(ポアソン分布)
model = smf.glm(formula=formula, data=data, family=family)
# モデリング(正規分布)
model_gauss = smf.glm(formula=formula, data=data, family=family_gauss)
# 推定
result = model.fit()
result_gauss = model_gauss.fit()
モデリングの結果を出力
print("=====モデリング結果=====")
print()
print(result.summary())
print("=====モデリング結果(model_gauss)=====")
print()
print(result_gauss.summary())
出力結果のLog-Likelihoodの項目を確認します。これは対数尤度の値を示しており、大きいほど推定に用いたデータに対する当てはまりが良いことを表しています。今回はポアソン分布のモデルが -1689.2、正規分布モデルが-1673.1 となり、あまり大きな差は見られません。
モデル評価の基準 AIC を出力して比較します。
# AIC の確認
print("AIC")
print(result.aic)
print()
print("AIC(model_gauss)")
print(result_gauss.aic)
print()
AIC
3382.3210451034556
AIC(model_gauss)
3350.151117225073
正規分布モデルの方が AIC が低いことから、RM と PRICE のモデルにおいて正規分布モデルの方が「予測の良さ」が高いということができます。
モデルでフィッティング
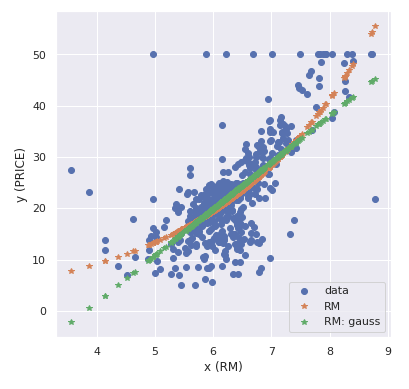
おまけとして、モデリングしたフィッティングの曲線をデータ点上にプロットします。
y_hat = result.predict(x)
y_hat_gauss = result_gauss.predict(x)
fig = plt.figure(figsize=(6.0, 6.0))
plt.plot(x_train["RM"], y_train, "o", label="data")
plt.plot(x_train["RM"], y_hat, "*", label="RM")
plt.plot(x_train["RM"], y_hat_gauss, "*", label="RM: gauss")
plt.xlabel('x (RM)'), plt.ylabel('y (PRICE)')
plt.legend()
plt.show()
所感
学びっぱなしになっていた一般化線形モデルについてまとめることができて良かったです。
ビジネスの現場では予測が重視される場合もありますが、現象と向き合ってそれに合うモデルを仮定するという方法は個人的には好きですね。
実際に使うにあたっては、確率分布の選定方法などまだまだ不明な部分が多いので、引き続き学んでいきたいと思います。
次回は@y_konoさんです。お楽しみに!